鲁科版高中化学选择性必修2第3章不同聚集状态的物质与性质3.2.5关于晶胞结构的拓展分析与计算课件(28张)
文档属性
| 名称 | 鲁科版高中化学选择性必修2第3章不同聚集状态的物质与性质3.2.5关于晶胞结构的拓展分析与计算课件(28张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 化学 | ||
| 更新时间 | 2025-08-12 08:56:56 | ||
图片预览



文档简介
(共28张PPT)
课时5 关于晶胞结构的拓展分析与计算
第3章 不同凝聚状态的物质与性质
2
1
晶体密度的相关计算
空间利用率
5
4
原子分数坐标参数
俯视图有关的晶体分析
3
配位数
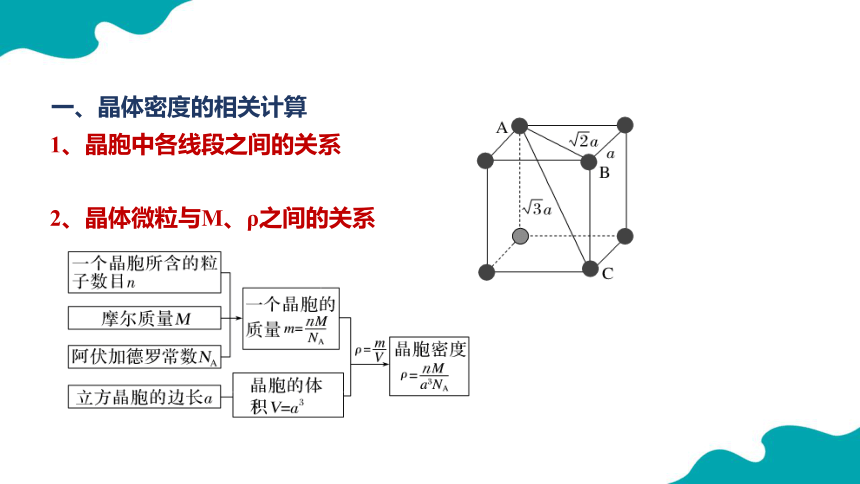
一、晶体密度的相关计算
1、晶胞中各线段之间的关系
2、晶体微粒与M、ρ之间的关系
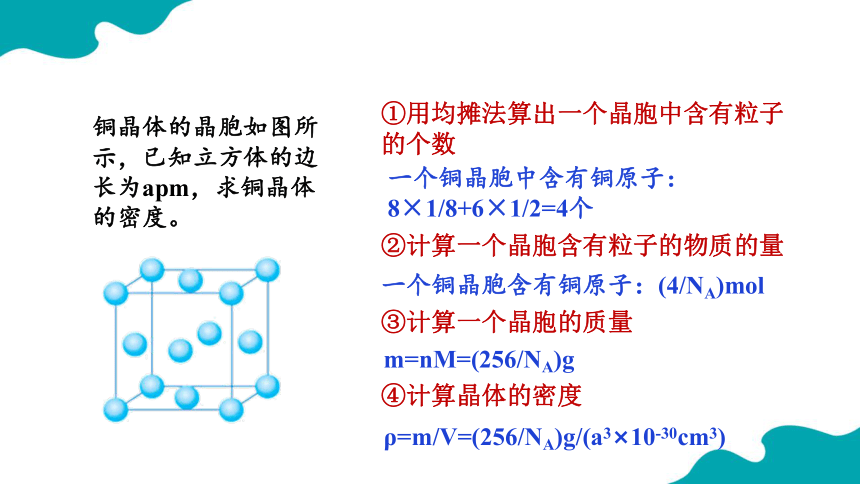
铜晶体的晶胞如图所示,已知立方体的边长为apm,求铜晶体的密度。
①用均摊法算出一个晶胞中含有粒子的个数
一个铜晶胞中含有铜原子:8×1/8+6×1/2=4个
②计算一个晶胞含有粒子的物质的量
一个铜晶胞含有铜原子:(4/NA)mol
③计算一个晶胞的质量
m=nM=(256/NA)g
④计算晶体的密度
ρ=m/V=(256/NA)g/(a3×10-30cm3)
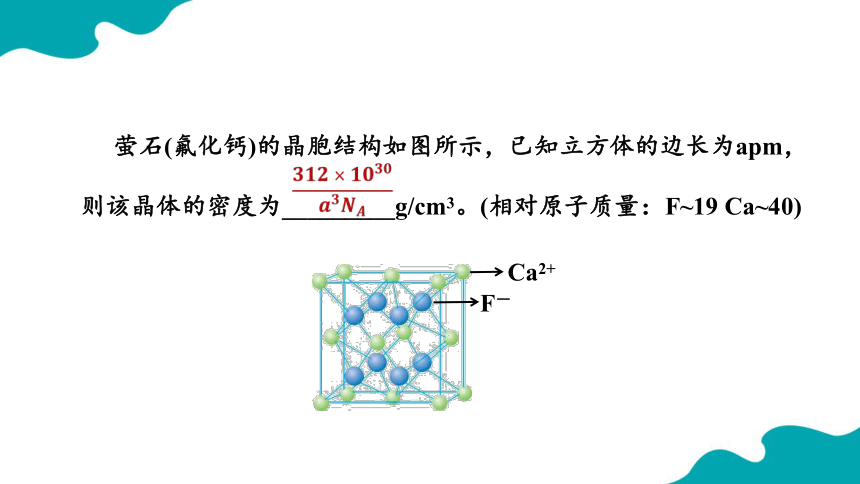
萤石(氟化钙)的晶胞结构如图所示,已知立方体的边长为apm,则该晶体的密度为_________g/cm3。(相对原子质量:F~19 Ca~40)
Ca2+
F-
二、空间利用率
空间利用率是指构成晶体的原子、离子或分子在整个晶体空间中所占的体积百分比,也叫空间占有率。
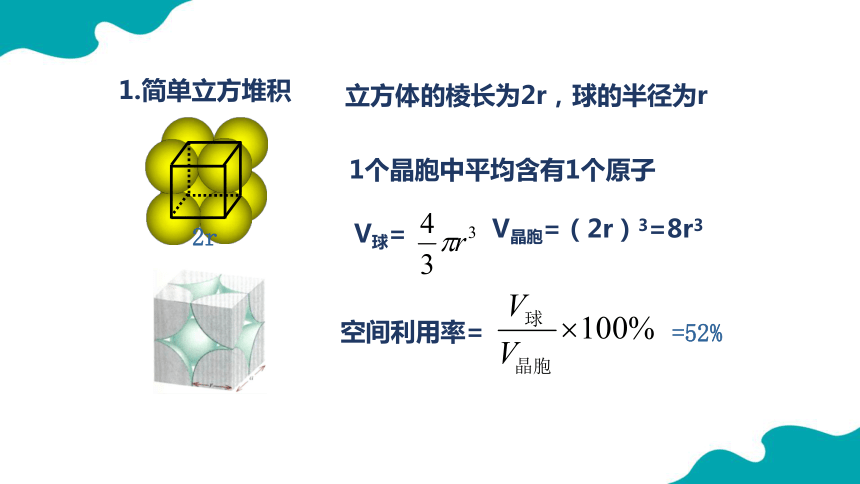
1.简单立方堆积
立方体的棱长为2r,球的半径为r
2r
1个晶胞中平均含有1个原子
V球=
V晶胞=(2r)3=8r3
空间利用率=
=52%
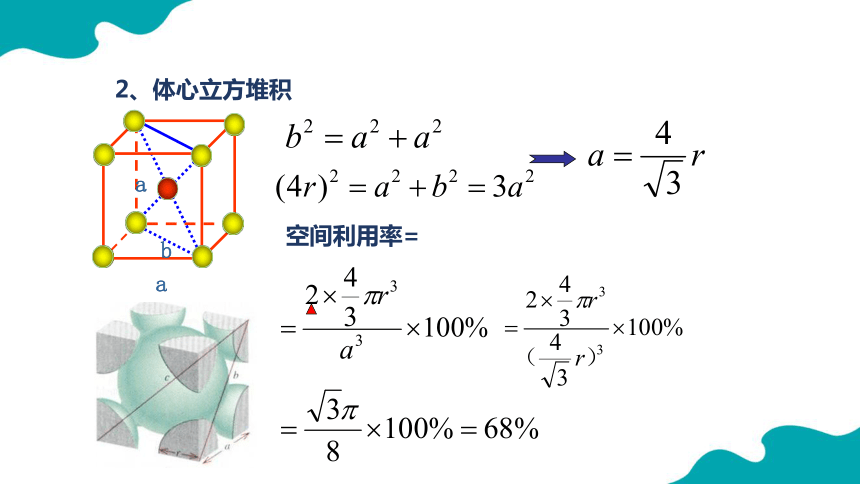
2、体心立方堆积
a
b
空间利用率=
a
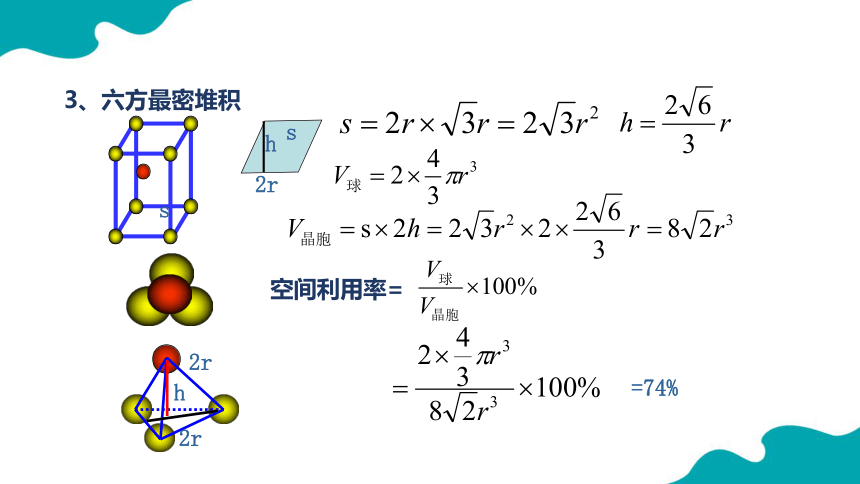
3、六方最密堆积
s
2r
h
2r
2r
=74%
空间利用率=
s
h
4、面心立方最密堆积
4r
a
=74%
空间利用率=
面心立方
简单立方
体心立方
六方堆积
面心立方
六方
体心立方
简单立方
74%
74%
68%
52%
12
12
8
6
Cu、Ag、Au
Mg、Zn、Ti
Na、K、Fe
Po
金属铜是面心立方晶体,有较多的滑移面,所以有很好的延展性。其晶胞结构如图乙所示。已知铜原子的半径为rcm,铜的密度为ρ g cm 3,阿伏加德罗常数为NAmol 1,该晶胞中铜原子的空间利用率为______________(用含r、ρ、NA的代数式表示)。
三、配位数
简单立方堆积的配位数:6
简单立方堆积
体心立方堆积的配位数:8
体心立方堆积
面心立方堆积的配位数:12
面心立方堆积
①顶点原子的配位原子在棱心,配位数为6
②顶点原子的配位原子在面心,配位数为12
思考:面心原子的配位数是多少?
4
③顶点原子的配位原子在体心,配位数为8
某晶体结构模型如图所示。该晶体的化学式是____________,在晶体中1个Ti原子、1个Co原子周围距离最近的O原子数目分别为________个、________个。
CoTiO3
6
12
四、原子分数坐标参数
(1)依据已知原子的坐标确定坐标系取向。
(2)一般以坐标轴所在正方体的棱长为1个单位。
(3)从原子所在位置分别向x、y、z轴作垂线,所得坐标轴上的截距即为该原子的分数坐标。
1、概念
原子分数坐标参数,表示晶胞内部各原子的相对位置。
2、原子分数坐标的确定方法
五、俯视图有关的晶体分析
四、俯视图有关的晶体分析
③阿伏加德罗常数的值为NA,该晶体的密度ρ=_____g·cm-3(列出计算式)。
4.硅化镁是一种窄带隙n型半导体材料,在光电子器件、能源器件、激光、半导体制造等领域具有重要应用前景。硅化镁的晶胞参数a=0.639 1 nm,属于面心立方晶胞,结构如图所示。
金刚石晶胞结构如图所示,回答下列问题。
(1)一个金刚石晶胞中含有___个碳原子。
(2)已知晶胞参数为a pm,则金刚石的密度为____________g·cm-3。
(3)晶体中两个最近的碳原子之间的距离为____ pm。
(4)碳原子半径为rpm,则a、r的关系为_______。
8
课时5 关于晶胞结构的拓展分析与计算
第3章 不同凝聚状态的物质与性质
2
1
晶体密度的相关计算
空间利用率
5
4
原子分数坐标参数
俯视图有关的晶体分析
3
配位数
一、晶体密度的相关计算
1、晶胞中各线段之间的关系
2、晶体微粒与M、ρ之间的关系
铜晶体的晶胞如图所示,已知立方体的边长为apm,求铜晶体的密度。
①用均摊法算出一个晶胞中含有粒子的个数
一个铜晶胞中含有铜原子:8×1/8+6×1/2=4个
②计算一个晶胞含有粒子的物质的量
一个铜晶胞含有铜原子:(4/NA)mol
③计算一个晶胞的质量
m=nM=(256/NA)g
④计算晶体的密度
ρ=m/V=(256/NA)g/(a3×10-30cm3)
萤石(氟化钙)的晶胞结构如图所示,已知立方体的边长为apm,则该晶体的密度为_________g/cm3。(相对原子质量:F~19 Ca~40)
Ca2+
F-
二、空间利用率
空间利用率是指构成晶体的原子、离子或分子在整个晶体空间中所占的体积百分比,也叫空间占有率。
1.简单立方堆积
立方体的棱长为2r,球的半径为r
2r
1个晶胞中平均含有1个原子
V球=
V晶胞=(2r)3=8r3
空间利用率=
=52%
2、体心立方堆积
a
b
空间利用率=
a
3、六方最密堆积
s
2r
h
2r
2r
=74%
空间利用率=
s
h
4、面心立方最密堆积
4r
a
=74%
空间利用率=
面心立方
简单立方
体心立方
六方堆积
面心立方
六方
体心立方
简单立方
74%
74%
68%
52%
12
12
8
6
Cu、Ag、Au
Mg、Zn、Ti
Na、K、Fe
Po
金属铜是面心立方晶体,有较多的滑移面,所以有很好的延展性。其晶胞结构如图乙所示。已知铜原子的半径为rcm,铜的密度为ρ g cm 3,阿伏加德罗常数为NAmol 1,该晶胞中铜原子的空间利用率为______________(用含r、ρ、NA的代数式表示)。
三、配位数
简单立方堆积的配位数:6
简单立方堆积
体心立方堆积的配位数:8
体心立方堆积
面心立方堆积的配位数:12
面心立方堆积
①顶点原子的配位原子在棱心,配位数为6
②顶点原子的配位原子在面心,配位数为12
思考:面心原子的配位数是多少?
4
③顶点原子的配位原子在体心,配位数为8
某晶体结构模型如图所示。该晶体的化学式是____________,在晶体中1个Ti原子、1个Co原子周围距离最近的O原子数目分别为________个、________个。
CoTiO3
6
12
四、原子分数坐标参数
(1)依据已知原子的坐标确定坐标系取向。
(2)一般以坐标轴所在正方体的棱长为1个单位。
(3)从原子所在位置分别向x、y、z轴作垂线,所得坐标轴上的截距即为该原子的分数坐标。
1、概念
原子分数坐标参数,表示晶胞内部各原子的相对位置。
2、原子分数坐标的确定方法
五、俯视图有关的晶体分析
四、俯视图有关的晶体分析
③阿伏加德罗常数的值为NA,该晶体的密度ρ=_____g·cm-3(列出计算式)。
4.硅化镁是一种窄带隙n型半导体材料,在光电子器件、能源器件、激光、半导体制造等领域具有重要应用前景。硅化镁的晶胞参数a=0.639 1 nm,属于面心立方晶胞,结构如图所示。
金刚石晶胞结构如图所示,回答下列问题。
(1)一个金刚石晶胞中含有___个碳原子。
(2)已知晶胞参数为a pm,则金刚石的密度为____________g·cm-3。
(3)晶体中两个最近的碳原子之间的距离为____ pm。
(4)碳原子半径为rpm,则a、r的关系为_______。
8
