“12345”模型巩固练习(含解析)
图片预览

文档简介
中小学教育资源及组卷应用平台
“12345”模型巩固练习
一.选择题(共7小题)
1.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,连接AB,BC,则∠ABC的度数为( )
A.30° B.45° C.60° D.75°
2.如图,矩形ABCD中,AB=3,BC=4,以点B为圆心,适当长为半径画弧,分别交BC,BD于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线BP,过点C作BP的垂线分别交BD,AD于点M,N,则CN的长为( )
A. B. C.4 D.5
3.如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是( )
A. B.1 C. D.
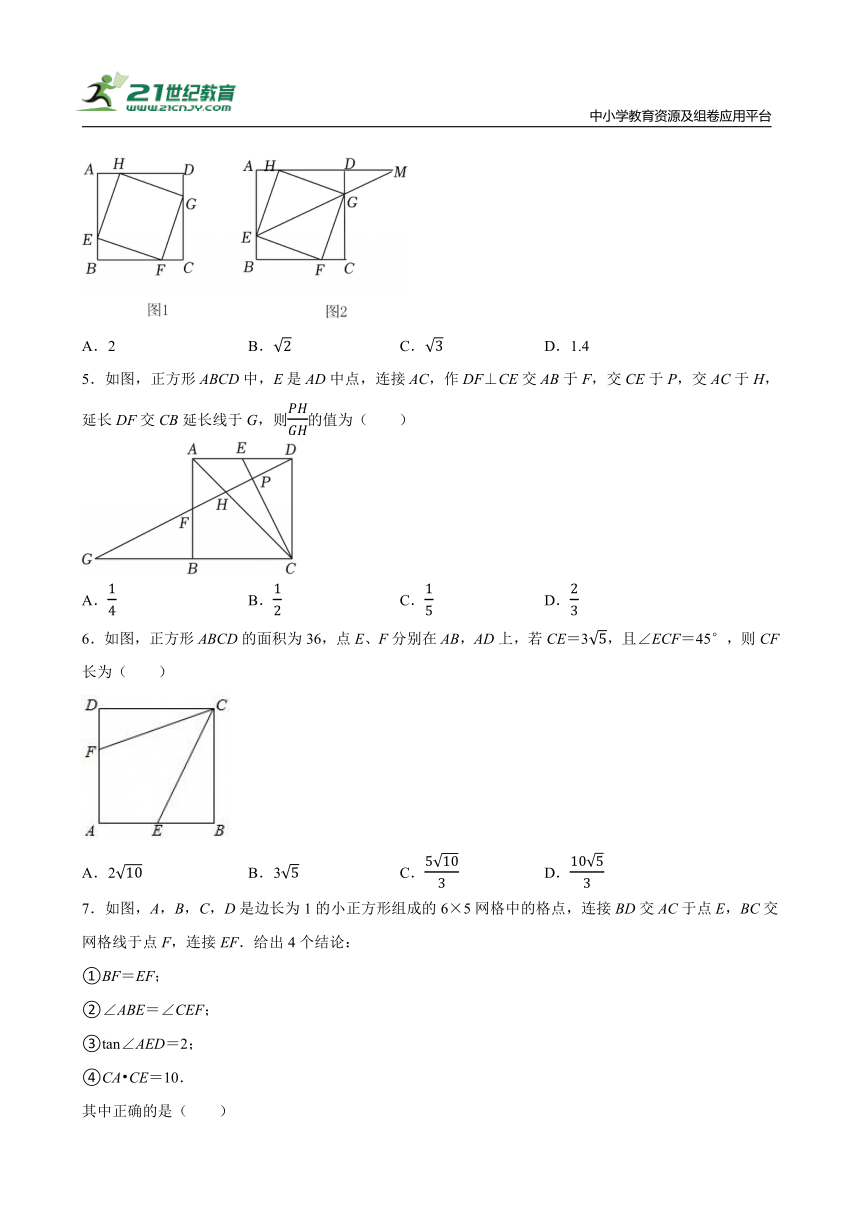
4.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图①),后人称之为“赵爽弦图”,流传至今,如图①是用四个全等的直角三角形拼成一个正方形,利用面积法可以证明勾股定理.如图2连接EG并延长交AD的延长线于点M,如,则的值为( )
A.2 B. C. D.1.4
5.如图,正方形ABCD中,E是AD中点,连接AC,作DF⊥CE交AB于F,交CE于P,交AC于H,延长DF交CB延长线于G,则的值为( )
A. B. C. D.
6.如图,正方形ABCD的面积为36,点E、F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF长为( )
A.2 B.3 C. D.
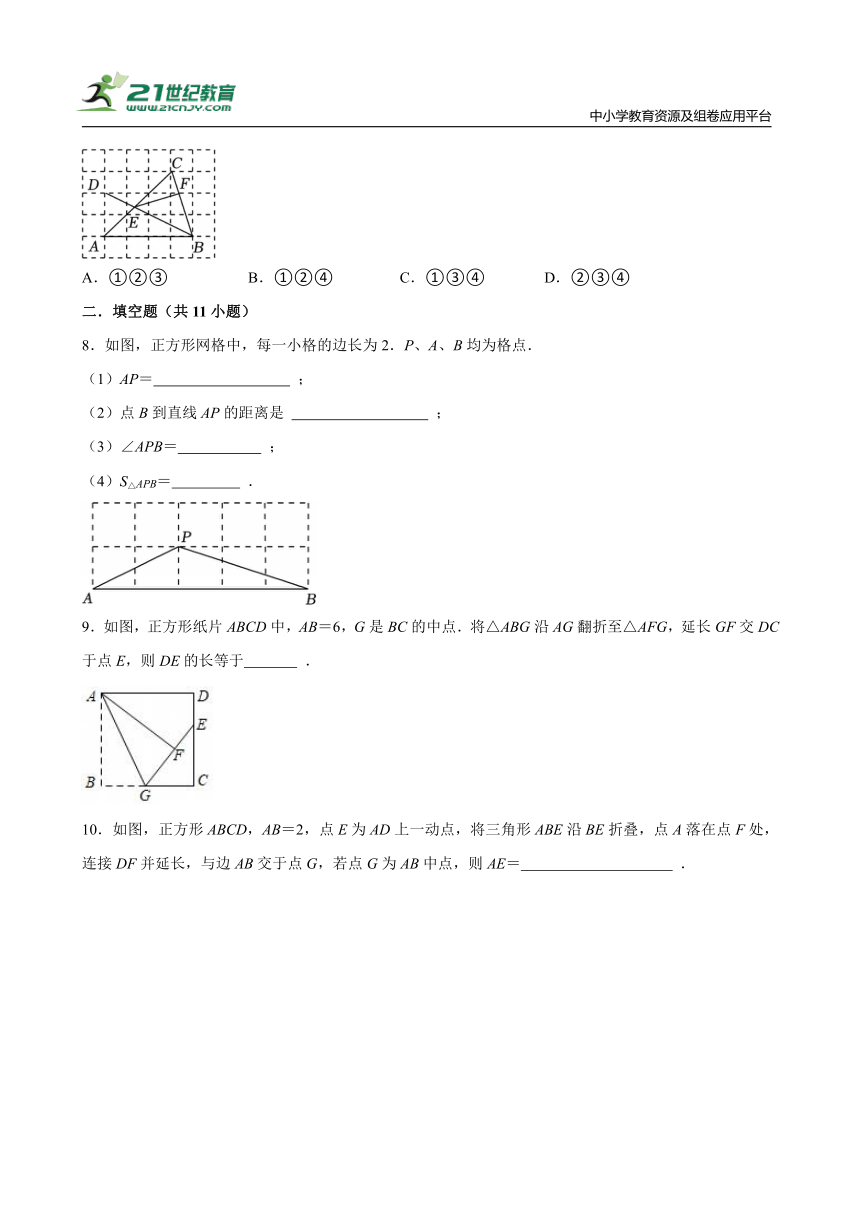
7.如图,A,B,C,D是边长为1的小正方形组成的6×5网格中的格点,连接BD交AC于点E,BC交网格线于点F,连接EF.给出4个结论:
①BF=EF;
②∠ABE=∠CEF;
③tan∠AED=2;
④CA CE=10.
其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
二.填空题(共11小题)
8.如图,正方形网格中,每一小格的边长为2.P、A、B均为格点.
(1)AP= ;
(2)点B到直线AP的距离是 ;
(3)∠APB= ;
(4)S△APB= .
9.如图,正方形纸片ABCD中,AB=6,G是BC的中点.将△ABG沿AG翻折至△AFG,延长GF交DC于点E,则DE的长等于 .
10.如图,正方形ABCD,AB=2,点E为AD上一动点,将三角形ABE沿BE折叠,点A落在点F处,连接DF并延长,与边AB交于点G,若点G为AB中点,则AE= .
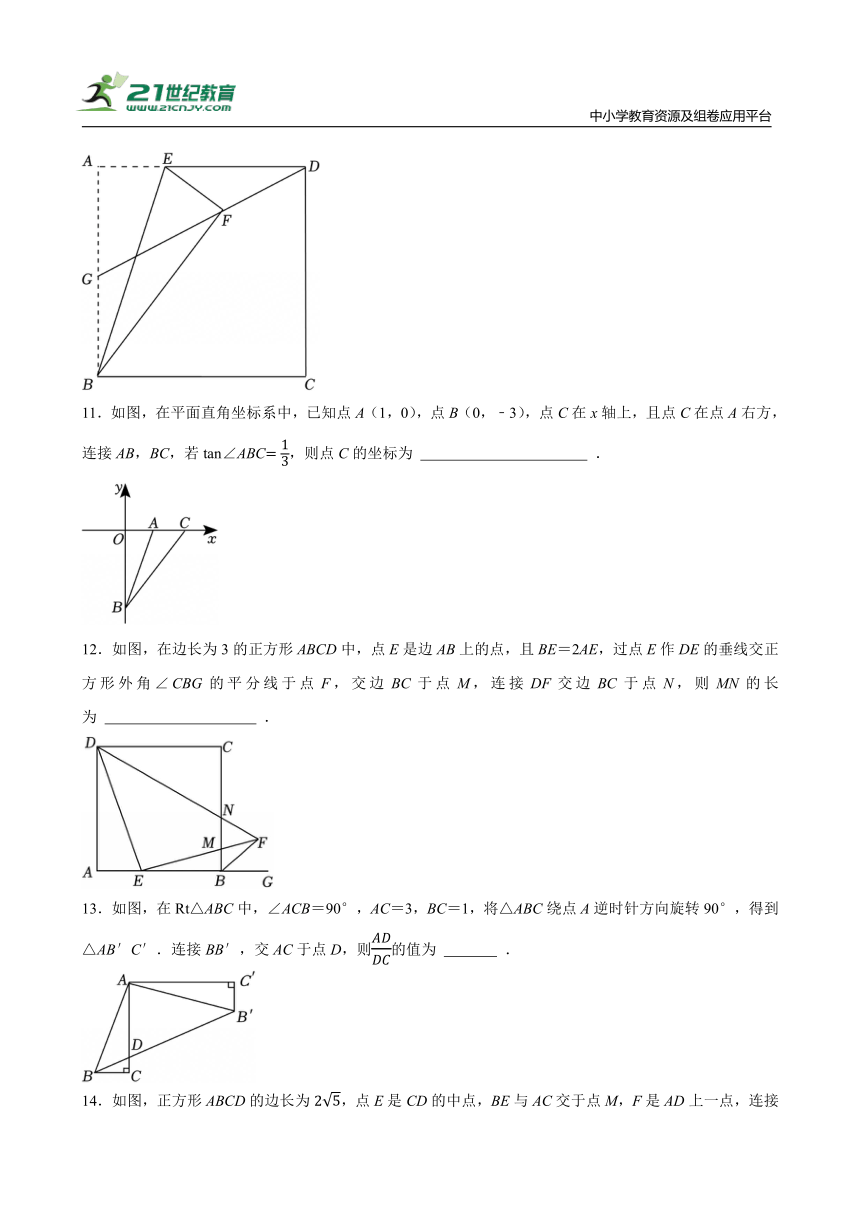
11.如图,在平面直角坐标系中,已知点A(1,0),点B(0,﹣3),点C在x轴上,且点C在点A右方,连接AB,BC,若tan∠ABC,则点C的坐标为 .
12.如图,在边长为3的正方形ABCD中,点E是边AB上的点,且BE=2AE,过点E作DE的垂线交正方形外角∠CBG的平分线于点F,交边BC于点M,连接DF交边BC于点N,则MN的长为 .
13.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=1,将△ABC绕点A逆时针方向旋转90°,得到△AB′C′.连接BB′,交AC于点D,则的值为 .
14.如图,正方形ABCD的边长为,点E是CD的中点,BE与AC交于点M,F是AD上一点,连接BF分别交AC,AE于点G,H,且BF⊥AE,连接MH,则AH= ,MH= .
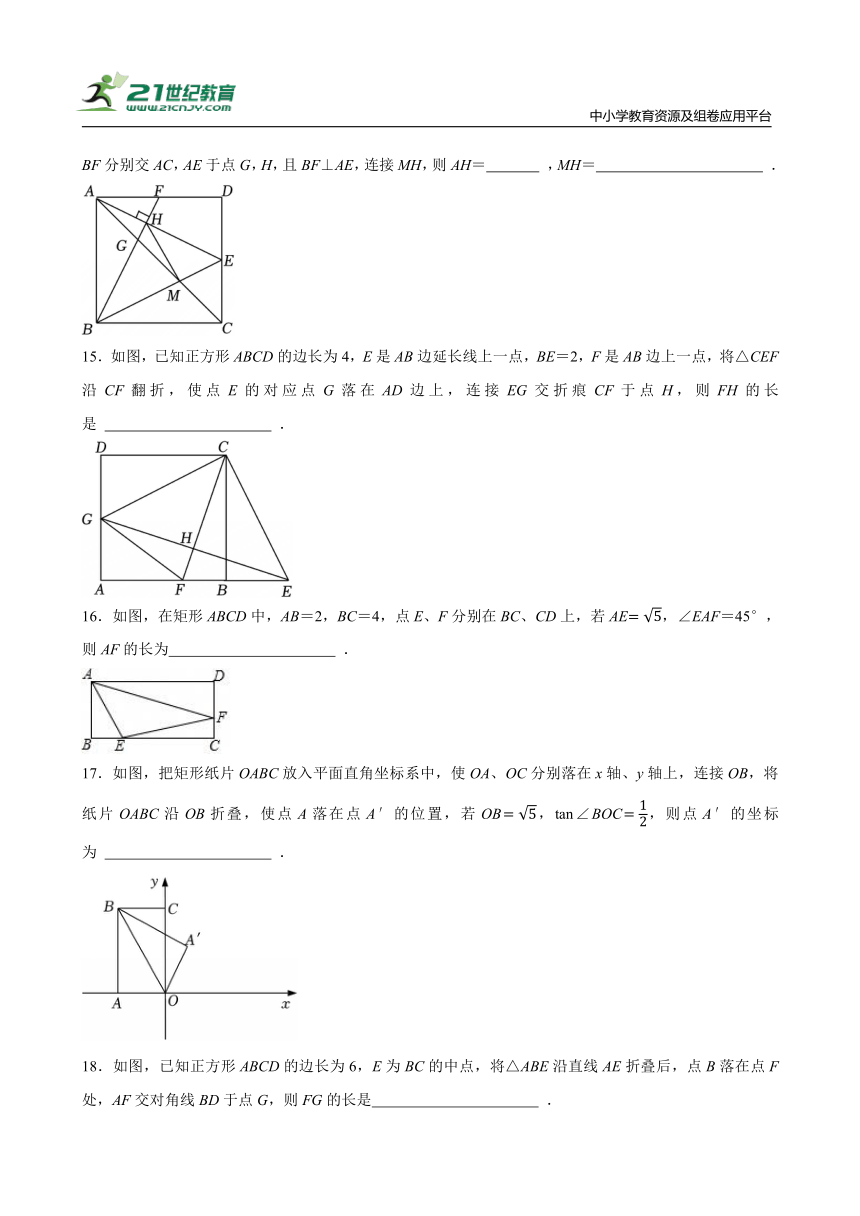
15.如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,BE=2,F是AB边上一点,将△CEF沿CF翻折,使点E的对应点G落在AD边上,连接EG交折痕CF于点H,则FH的长是 .
16.如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE,∠EAF=45°,则AF的长为 .
17.如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在点A′的位置,若OB,tan∠BOC,则点A′的坐标为 .
18.如图,已知正方形ABCD的边长为6,E为BC的中点,将△ABE沿直线AE折叠后,点B落在点F处,AF交对角线BD于点G,则FG的长是 .
“12345”模型巩固练习
一.选择题(共7小题)
题号 1 2 3 4 5 6 7
答案 B A C B C A B
一.选择题(共7小题)
1.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,连接AB,BC,则∠ABC的度数为( )
A.30° B.45° C.60° D.75°
【分析】根据勾股定理即可得到AB,BC,AC的长度,进行判断即可.
【解答】解:根据勾股定理可以得到:AC=BC,AB=2.
∵())2+()2=(2)2.
∴AC2+BC2=AB2.
∴△ABC是等腰直角三角形.
∴∠ABC=45°.
故选:B.
【点评】本题考查了勾股定理,判断△ABC是等腰直角三角形是解决本题的关键.
2.如图,矩形ABCD中,AB=3,BC=4,以点B为圆心,适当长为半径画弧,分别交BC,BD于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线BP,过点C作BP的垂线分别交BD,AD于点M,N,则CN的长为( )
A. B. C.4 D.5
【分析】先证明三角形全等,再根据勾股定理求解.
【解答】解:设CN交BP于点Q,
在矩形ABCD中,∠BCD=∠ADC=90°,AD∥BC,
∵AB=3,BC=4,
∴BD=5,
由作图得:BP平分∠CBD,
∴∠DBP=∠CBP,
∵过点C作BP的垂线分别交BD,AD于点M,N,
∴∠MQB=∠CQB=90°,
∵BQ=BQ,
∴△BQM≌△BQC(ASA),
∴BM=BC=4,∠CMB=∠MCB,
∴DM=BD﹣BM=1,
∵AD∥BC,
∴∠DNC=∠NCB,
∵∠DMN=∠CMB,
∴∠DNC=∠NMD,
∴DN=DM=1,
∴NC,
故选:A.
【点评】本题考查了作图﹣基本作图,掌握三角形全等是性质及勾股定理是解题的关键.
3.如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是( )
A. B.1 C. D.
【分析】连接AF,由矩形的性质得出∠B=∠C=90°,CD=AB=2,BC=AD=3,证出AB=FC,BF=CE,由SAS证明△ABF≌△FCE,得出∠BAF=∠CFE,AF=FE,证△AEF是等腰直角三角形,得出∠AEF=45°,即可得出答案.
【解答】解:连接AF,如图所示:
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD=AB=2,BC=AD=3,
∵FC=2BF,
∴BF=1,FC=2,
∴AB=FC,
∵E是CD的中点,
∴CECD=1,
∴BF=CE,
在△ABF和△FCE中,
,
∴△ABF≌△FCE(SAS),
∴∠BAF=∠CFE,AF=FE,
∵∠BAF+∠AFB=90°,
∴∠CFE+∠AFB=90°,
∴∠AFE=180°﹣90°=90°,
∴△AEF是等腰直角三角形,
∴∠AEF=45°,
∴cos∠AEF;
故选:C.
【点评】本题考查了矩形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、三角函数等知识;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.
4.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图①),后人称之为“赵爽弦图”,流传至今,如图①是用四个全等的直角三角形拼成一个正方形,利用面积法可以证明勾股定理.如图2连接EG并延长交AD的延长线于点M,如,则的值为( )
A.2 B. C. D.1.4
【分析】在Rt△DGM中,根据,设DG=x,DM=2x,从而利用勾股定理求出GM,再设HD=y,根据题意可得AE=HD=y,AH=DG=x,从而求出AM,然后在Rt△AEM中,利用锐角三角函数的定义可得,从而求出y=3x,最后在Rt△HDG中,利用勾股定理求出HG,进行计算即可解答.
【解答】解:tanM,
∴,
∴设DG=x,DM=2x,
∴,
设HD=y,
由题意得:△AEH≌△DHG,
∴AE=HD=y,AH=DG=x,
,
∴,
∴3x+y=2y,
∴y=3x,
∴DH=y=3x,
∴,
∴,
故选:B.
【点评】本题考查了勾股定理的证明,解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.
5.如图,正方形ABCD中,E是AD中点,连接AC,作DF⊥CE交AB于F,交CE于P,交AC于H,延长DF交CB延长线于G,则的值为( )
A. B. C. D.
【分析】先证明△ADF≌△DCE,得AF=DEAB,根据AD∥BC证明△ADF∽△BGF,△ADH∽△CGH,△DEP∽△GCP,列比例式可求得:PH和GH的长,从而得结论.
【解答】解:∵四边形ABCD是正方形,
∴AD=CD,∠BAD=∠ADC=90°,
∴∠ADF+∠CDP=90°,
∵DF⊥CE,
∴∠CPD=90°,
∴∠DCE+∠CDP=90°,
∴∠ADF=∠DCE,
∴△ADF≌△DCE(ASA),
∴AF=DE,
∵点E是AD的中点,
∴DEAD,
∴AFAB,
∵四边形ABCD是正方形,
∴AD∥BC,
∴△ADF∽△BGF,△ADH∽△CGH,△DEP∽△GCP,
∴1,,,
设PD=a,则PG=4a,
∴DHa,GHa
∴PH=DH﹣PDa﹣aa
∴.
故选:C.
【点评】本题考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解决问题的关键是弄清比例之间的数量关系.
6.如图,正方形ABCD的面积为36,点E、F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF长为( )
A.2 B.3 C. D.
【分析】首先延长FD到G,使DG=BE,利用正方形的性质得∠B=∠CDF=∠CDG=90°,CB=CD;利用SAS定理得△BCE≌△DCG,利用全等三角形的性质易得△GCF≌△ECF,利用勾股定理可得AE=3,设AF=x,利用GF=EF,解得x,利用勾股定理可得CF.
【解答】解:∵正方形ABCD的面积为36,
∴BC=AB=6,
如图,延长FD到G,使DG=BE;
连接CG、EF;
∵四边形ABCD为正方形,
在△BCE与△DCG中,,
∴△BCE≌△DCG(SAS),
∴CG=CE,∠DCG=∠BCE,
∴∠GCF=45°,
在△GCF与△ECF中,,
∴△GCF≌△ECF(SAS),
∴GF=EF,
∵CE=3,CB=6,
∴BE=3,
∴AE=3,
设AF=x,则DF=6﹣x,GF=3+(6﹣x)=9﹣x,
∴EF,
∴(9﹣x)2=9+x2,
∴x=4,
即AF=4,
∴DF=6﹣4=2,
∴CF2,
故选:A.
【点评】本题主要考查了正方形的性质,全等三角形的判定及性质,勾股定理等,构建全等三角形,利用方程思想是解答此题的关键.
7.如图,A,B,C,D是边长为1的小正方形组成的6×5网格中的格点,连接BD交AC于点E,BC交网格线于点F,连接EF.给出4个结论:
①BF=EF;
②∠ABE=∠CEF;
③tan∠AED=2;
④CA CE=10.
其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
【分析】连接CD,利用全等三角形的判定与性质得到∠DCB=90°,则△CDB为等腰直角三角形;利用角平分线的性质定理和平行线分线段成比例定理得到2,则EF∥CD,利用平行线的性质得到∠FEB=∠CDB=45°,则△FEB为等腰直角三角形,则得①的结论正确;利用三角形的内角和定理得到∠ABE=∠DCE,利用两直线平行,内错角相等得到∠CEF=∠DCE,则②的结论正确;利用三角形的外交的性质得到∠AED=∠CBA,在Rt△CHB中,利用直角三角形的边角关系定理得到tan∠CBA3,则得③的结论不正确;利用相似三角形的判定与性质,列出比例式计算,则得④的结论正确.
【解答】解:连接CD,G,H为格点,如图,
由题意得:AD=2,AB=4,CD=CB,∠DAC=∠BAC=45°.
在△DCG和△CBH中,
,
∴△DCG≌△CBH(SAS),
∴∠DCG=∠CBH,
∵∠CBH+∠BCH=90°,
∴∠DCG+∠BCH=90°,
∴∠DCB=90°,
∴△DCB为等腰直角三角形,
∴∠CDB=∠CBD=45°.
∵∠DAC=∠BAC=45°,
∴2,
∵FG∥BH,
∴2,
∴,
∴EF∥CD,
∴∠FEB=∠CDB=45°,
∴∠FEB=∠CBD=45°,
∴BF=EF.
∴①的结论正确;
∵∠CAB=∠CDB=45°,∠AEB=∠DEC,
∴∠ABE=∠DCE.
∵EF∥CD,
∴∠CEF=∠DCE,
∴∠ABE=∠CEF.
∴②的结论正确;
∵∠AED=∠EAB+∠ABE=45°+∠ABE,∠CBA=∠CBD+∠ABE=45°+∠ABE,
∴∠AED=∠CBA,
在Rt△CHB中,
tan∠CBA3,
∴tan∠AED=tan∠CBA=3,
∴③的结论不正确;
∵∠CBD=∠CAB=45°,∠ECB=∠BCA,
∴△BCE∽△ACB,
∴,
∴CA CE=CB210,
∴④的结论正确.
综上,正确的结论有:①②④.
故选:B.
【点评】本题主要考查了解直角三角形,直角三角形的性质,勾股定理,相似三角形的判定与性质平行线的判定与性质,平行线分线段成比例定理,等腰直角三角形的判定与性质,本题是网格题,熟练掌握网格的特性是解题的关键.
二.填空题(共11小题)
8.如图,正方形网格中,每一小格的边长为2.P、A、B均为格点.
(1)AP= 2 ;
(2)点B到直线AP的距离是 2 ;
(3)∠APB= 135° ;
(4)S△APB= 10 .
【分析】(1)用勾股定理求解即可;
(2)延长AP得格点C,连接BC,PC,证∠BCP=90°,则点B到直线AP的距离是线段BC的长,再由勾股定理求出BC的长即可;
(3)由(2)问图可证△BPC是等腰直角三角形,从而得∠BPC=45°,即可由∠APB=180°﹣∠BPC求解;
(4)根据三角形面积公式计算即可求解.
【解答】解:(1)1×2=2,
2×2=4,
AP2.
故答案为:2;
(2)延长AP得格点C,连接BC,PC,如图,
由图可得:PE=CD,CE=BD,∠PEC=∠BDC=90°,
∴△PEC≌△CDB(SAS),
∴∠PCE=∠CBD,
∴∠DCB+∠CBD=90°,
∴∠DCB+∠PCE=90°,
∴∠PCB=90°,
∴BC⊥AP,
∴点B到直线AP的距离是线段BC的长,
∴BC2.
故答案为:2;
(3)由(2)知△PEC≌△CDB(SAS),∠PCB=90°,
∴BC=PC,
∴△BPC是等腰直角三角形,
∴∠BPC=45°,
∴∠APB=180°﹣∠BPC=135°.
故答案为:135°;
(4)5×2=10,
10×2÷2=10.
故S△APB=10.
故答案为:10.
【点评】本题考查勾股定理,点到直线的距离,全等三角形的判定与性质,等腰直角三角形,熟练掌握在网格图用勾股定理求线段长是解题的关键.
9.如图,正方形纸片ABCD中,AB=6,G是BC的中点.将△ABG沿AG翻折至△AFG,延长GF交DC于点E,则DE的长等于 2 .
【分析】根据翻折变换的性质和正方形的性质可证Rt△AFE≌Rt△ADE;在直角△ECG中,根据勾股定理即可求出DE的长.
【解答】解:如图,连接AE,
∵AB=AD=AF,∠D=∠AFE=90°,
在Rt△AFE和Rt△ADE中,
∴Rt△AFE≌Rt△ADE,
∴EF=DE,
设DE=FE=x,则EC=6﹣x.
∵G为BC中点,BC=6,
∴CG=3,
在Rt△ECG中,根据勾股定理,得:(6﹣x)2+32=(x+3)2,
解得x=2.
则DE=2.
故答案为2.
【点评】本题考查了翻折变换,解题的关键是掌握翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理.
10.如图,正方形ABCD,AB=2,点E为AD上一动点,将三角形ABE沿BE折叠,点A落在点F处,连接DF并延长,与边AB交于点G,若点G为AB中点,则AE= .
【分析】过点F作MN∥AB,分别交AD,BC于点M,N,根据点G为AB中点可得AG=1,不难推出四边形ABNM为矩形,△DMF∽△DAG,则,设MF=x,则DM=2x,AM=2﹣2x,NF=2﹣x,BN=AM=2﹣2x,根据折叠的性质可得AE=EF,AB=BF=2,根据勾股定理得BF2=BN2+NF2,以此得出,,设AE=y,则EF=y,EM=AD﹣DM﹣AE=2,再根据勾股定理得EF2=EM2+MF2,以此列出方程求解即可.
【解答】解:过点F作MN∥AB,分别交AD,BC于点M,N,如图,
,
∵四边形ABCD为正方形,
∴∠A=90°,AB=AD=2,四边形ABNM为矩形,
∴AM=BN,AB=MN=2,
∵点G为AB中点,
∴1,
∵MN∥AB,
∴△DMF∽△DAG,
∴,
即DM=2MF,
设MF=x,则DM=2x,AM=2﹣2x,NF=2﹣x,
∴BN=AM=2﹣2x,
根据折叠的性质得,AE=EF,AB=BF=2,
在Rt△BNF中,
根据勾股定理得,BF2=BN2+NF2,
∴22=(2﹣2x)2+(2﹣x)2,
整理得,5x2﹣12x+4=0,
解得:或2(舍去),
∴,,
设AE=y,则EF=y,EM=AD﹣DM﹣AE=2,
在Rt△EMF中,
由勾股定理得,EF2=EM2+MF2,
∴,
∴y,
∴AE.
故答案为:.
【点评】本题主要考查折叠的性质、相似三角形的判定与性质、勾股定理、正方形的性质,正确作出辅助线,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案是解题关键.
11.如图,在平面直角坐标系中,已知点A(1,0),点B(0,﹣3),点C在x轴上,且点C在点A右方,连接AB,BC,若tan∠ABC,则点C的坐标为 (,0) .
【分析】设C(a,0),结合A,B两点的坐标利用两点间的距离可得OA=1,AC=a﹣1,OB=3,BC,通过解直角三角形可得∠OBA=∠ABC,过C点作CD∥y轴交BA的延长线于点D,利用平行线的性质可得△OBA∽△CDA,∠ABC=∠D,列比例式再代入计算可求解a值,进而可求解.
【解答】解:设C(a,0),
∴OC=a,
∵点A(1,0),点B(0,﹣3),
∴OA=1,AC=a﹣1,OB=3,BC,
在Rt△OAB中,tan∠OBA,tan∠ABC,
∴∠OBA=∠ABC,
过C点作CD∥y轴交BA的延长线于点D,
∴∠OBA=∠D,∠AOB=∠ACD,
∴△OBA∽△CDA,∠ABC=∠D,
∴,CD=BC,
∴,
∴,
解得a=0(舍去)或a,
∴C(,0),
故答案为:(,0).
【点评】本题主要考查坐标与图形的性质,相似三角形的判定与性质,等腰三角形的性质,平行线的性质,两点间的距离等知识的综合运用,作适当的辅助线是解题的关键.
12.如图,在边长为3的正方形ABCD中,点E是边AB上的点,且BE=2AE,过点E作DE的垂线交正方形外角∠CBG的平分线于点F,交边BC于点M,连接DF交边BC于点N,则MN的长为 .
【分析】根据正方形的性质、相似三角形的判定和性质,可以求得CN和BM的长,然后根据BC=3,即可求得MN的长.
【解答】解:作FH⊥BG交于点H,作FK⊥BC于点K,
∵BF平分∠CBG,∠KBH=90°,
∴四边形BHFK是正方形,
∵DE⊥EF,∠EHF=90°,
∴∠DEA+∠FEH=90°,∠EFH+∠FEH=90°,
∴∠DEA=∠EFH,
∵∠A=∠EHF=90°,
∴△DAE∽△EHF,
∴,
∵正方形ABCD的边长为3,BE=2AE,
∴AE=1,BE=2,
设FH=a,则BH=a,
∴,
解得a=1;
∵FK⊥CB,DC⊥CB,
∴△DCN∽△FKN,
∴,
∵BC=3,BK=1,
∴CK=2,
设CN=b,则NK=2﹣b,
∴,
解得b,
即CN,
∵∠A=∠EBM,∠AED=∠BME,
∴△ADE∽△BEM,
∴,
∴,
解得BM,
∴MN=BC﹣CN﹣BM=3.
故答案为:.
【点评】本题考查正方形的性质、相似三角形的判定和性质,解答本题的关键是明确题意,利用数形结合的思想解答.
13.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=1,将△ABC绕点A逆时针方向旋转90°,得到△AB′C′.连接BB′,交AC于点D,则的值为 5 .
【分析】过点D作DF⊥AB于点F,利用勾股定理求得 AB,根据旋转的性质可证△ABB'、△DFB 是等腰直角三角形,可得DF=BF,再由S△ADBBCDF×AB,ADDF,证明△AFD∽△ACB,可得 ,即AF=3DF,再由 ,求得 ,从而求得 ,,即可求解.
【解答】解:过点D作DF⊥AB于点F,
,
∵∠ACB=90°,AC=3,BC=1,,
∵将△ABC绕点A逆时针方向旋转 90° 得到△AB'C',,∠BAB'=90°,
∴△ABB'是等腰直角三角形,
∴∠ABB'=45°
∵DF⊥AB,∠DFB=90°,
∴△DFB是等腰直角三角形,
∴DF=BF,
S△DBABC×ADDF×AB,即 ,
∵∠C=∠AFD=90°,∠CAB=∠FAD,
∴△AFD∽△ACB,
∴,
即AF=3DF,
又∵,
∴,
∴,
∴,
∴5,
故答案为:5.
【点评】本题考查旋转的性质、等腰三角形的判定与性质、相似三角形的判定与性质、三角形的面积,则 练掌握相关知识是解题的关键.
14.如图,正方形ABCD的边长为,点E是CD的中点,BE与AC交于点M,F是AD上一点,连接BF分别交AC,AE于点G,H,且BF⊥AE,连接MH,则AH= 2 ,MH= .
【分析】先求出AE=5,证△DAE和△ABF全等得DE=AF,AE=BF=5,再证△AFH∽△ADE,利用相似三角形的性质可得AH的长;过点M作MN⊥AE于点N,先求出AE=BE=5,EH=3,BH=4,证△MEC∽△MBA得ME:MB=CE:AB=1:2,进而得ME:EB=1:3,再证△MNE∽△BHE,利用相似三角形的性质得MN,EN=1,进而得HN=2,最后在Rt△MHN中,由勾股定理可求出MH.
【解答】解:∵四边形ABCD为正方形,且边长为,
∴AB=BC=CD=DA,∠BAD=∠D=90°,AB∥CD,
∵点E为CD的中点,
∴DE=CE,
在Rt△ADE中,AD,DE,
由勾股定理得:,
∵∠BAD=90°,BF⊥AE,
∴∠BAH+∠DAE=90°,∠ABF+∠BAH=90°,
∴∠DAE=∠ABF,
在△DAE和△ABF中,
,
∴△DAE≌△ABF(SAS),
∴DE=AF,AE=BF=5,
∵BF⊥AE,∠D=90°,
∴∠AHF=∠D=90°,
又∠HAF=∠DAE,
∴△AFH∽△ADE,
∴AH:AD=AF:AE,
即:AH::5,
∴AH=2.
过点M作MN⊥AE于点N,如图:
在△ADE和△BCE中,
,
∴△ADE≌△BCE(SAS),
∴AE=BE=5,
∴EH=AE﹣AH=5﹣2=3,
在Rt△AHB中,AB,AH=2,
由勾股定理得:,
∵AB∥CD,
∴△MEC∽△MBA,
∴ME:MB=CE:AB,
即:ME:MB:2,
∴ME:MB=1:2,
∴ME:EB=1:3,
∵BF⊥AE,MN⊥AE,
∴MN∥BH,
∴△MNE∽△BHE,
∴MN:BH=EN:EH=ME:EB
∴MN:4=EN:3=1:3,
∴MN,EN=1,
∴HN=EH﹣EN=3﹣1=2,
在Rt△MHN中,MN,HN=2,
由勾股定理得:.
故答案为:2,.
【点评】此题主要考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,熟练掌握全等三角形的判定和性质,灵活运用相似三角形的性质和勾股定理进行计算是解答此题的关键.
15.如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,BE=2,F是AB边上一点,将△CEF沿CF翻折,使点E的对应点G落在AD边上,连接EG交折痕CF于点H,则FH的长是 .
【分析】由正方形的性质得AB=AD=CD=CB=4,∠A=∠D=∠ABC=90°,则∠CBE=90°,由翻折得CG=CE,则DGBE=2,所以AG=2,AE=6,则EG2,因为CF垂直平分EG,所以GF=EF,由勾股定理得22+(6﹣EF)2=EF2,求得EF,即可根据2FH2=S△EFG,求得FH,于是得到问题的答案.
【解答】解:∵四边形ABCD是边长为4的正方形,
∴AB=AD=CD=CB=4,∠A=∠D=∠ABC=90°,
∴∠CBE=90°,
由翻折得CG=CE,
∴DGBE=2,
∴AG=AD﹣DG=4﹣2=2,AE=AB+BE=4+2=6,
∴EG2,
∵点G与点E关于直线CF对称,
∴CF垂直平分EG,
∴GF=EF,
∵AG2+AF2=GF2,且AF=6﹣EF,
∴22+(6﹣EF)2=EF2,
解得EF,
∵EG FHEF AG=S△EFG,
∴2FH2,
解得FH,
故答案为:.
【点评】此题重点考查正方形的性质、轴对称的性质、勾股定理、根据面积等式求线段的长度等知识与方法,求得DG=2是解题的关键.
16.如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE,∠EAF=45°,则AF的长为 .
【分析】取AB的中点M,连接ME,在AD上截取ND=DF,设DF=DN=x,则NFx,再利用矩形的性质和已知条件证明△AME∽△FNA,利用相似三角形的性质:对应边的比值相等可求出x的值,在直角三角形ADF中利用勾股定理即可求出AF的长.
【解答】解:取AB的中点M,连接ME,在AD上截取ND=DF,设DF=DN=x,
∵四边形ABCD是矩形,
∴∠D=∠BAD=∠B=90°,AD=BC=4,
∴NFx,AN=4﹣x,
∵AB=2,
∴AM=BM=1,
∵AE,AB=2,
∴BE=1,
∴ME,
∵∠EAF=45°,
∴∠MAE+∠NAF=45°,
∵∠MAE+∠AEM=45°,
∴∠MEA=∠NAF,
∴△AME∽△FNA,
∴,
∴,
解得:x,
经检验,x是分式方程的解,
∴AF.
故答案为:.
【点评】本题考查了矩形的性质、相似三角形的判断和性质以及勾股定理的运用,正确添加辅助线构造相似三角形是解题的关键,
17.如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在点A′的位置,若OB,tan∠BOC,则点A′的坐标为 (,) .
【分析】过点A′作A′D⊥x轴于点D,根据题意首先求出AB、BC的长度;借助面积公式求出A′D、OD的长度,即可解决问题.
【解答】解:如图,过点A′作A′D⊥x轴于点D,
∵四边形ABCO为矩形,
∴∠AOC=∠OAB=∠OCB=90°,OA=BC,
∵OB,tan∠BOC,
∴OA=BC=1,OC=AB=2,
由折叠的性质得:A′O=AO=1,△ABO≌△EBO,
设A′D=x,OD=y;
由勾股定理得:x2+y2=1①,
由面积公式得:xy+22×1(x+2)(y+1)②;
联立①②并解得:x,y,
则点A′的坐标为(,).
故答案为:(,).
【点评】此题考查翻折变换,坐标与图形的性质;解决问题的关键是综合利用矩形的性质,勾股定理等几何知识点.
18.如图,已知正方形ABCD的边长为6,E为BC的中点,将△ABE沿直线AE折叠后,点B落在点F处,AF交对角线BD于点G,则FG的长是 .
【分析】延长AF,EF分别交CD于H,M,连接AM,根据折叠的性质得到AB=AF,∠ABE=∠AFE=90°,根据全等三角形的性质得到DM=FM,设DM=FM=x,则CM=6﹣x,EM=3+x,根据勾股定理得到DM=FM=2,根据相似三角形的判定和性质定理即可得到结论.
【解答】解:延长AF,EF分别交CD于H,M,连接AM,
∵四边形ABCD是正方形,
∴AB=AD,∠ABE=∠ADC=90°,
∵将△ABE沿直线AE折叠后,点B落在点F处,
∴AB=AF,∠ABE=∠AFE=90°,
∴∠ADM=∠AFM=90°,AF=AD,
∵AM=AM,
∴Rt△ADM≌Rt△AFM(HL),
∴DM=FM,
∵E为BC的中点,BC=CD=6,
∴CE=3,
设DM=FM=x,则CM=6﹣x,EM=3+x,
∵EM2=CM2+CE2,
∴(3+x)2=32+(6﹣x)2,
解得:x=2,
∴DM=FM=2,
∵∠MFH=∠ECM=90°,∠HMF=∠CME,
∴△MFH∽△MCE,
∴,
∴,
∴MH=2.5,FH=1.5,
∴AH=6+1.5=7.5,DH=4.5,
∵AB∥DH,
∴△AGB∽△HGD,
∴,
∴,
∴AG,
∴GF=AF﹣AG,
故答案为:.
【点评】本题考查了翻折变换(折叠问题),正方形的性质,全等三角形的判定和性质,勾股定理,相似三角形的判定和性质,正确的作出辅助线是解题的关键.
“12345”模型巩固练习
一.选择题(共7小题)
1.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,连接AB,BC,则∠ABC的度数为( )
A.30° B.45° C.60° D.75°
2.如图,矩形ABCD中,AB=3,BC=4,以点B为圆心,适当长为半径画弧,分别交BC,BD于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线BP,过点C作BP的垂线分别交BD,AD于点M,N,则CN的长为( )
A. B. C.4 D.5
3.如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是( )
A. B.1 C. D.
4.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图①),后人称之为“赵爽弦图”,流传至今,如图①是用四个全等的直角三角形拼成一个正方形,利用面积法可以证明勾股定理.如图2连接EG并延长交AD的延长线于点M,如,则的值为( )
A.2 B. C. D.1.4
5.如图,正方形ABCD中,E是AD中点,连接AC,作DF⊥CE交AB于F,交CE于P,交AC于H,延长DF交CB延长线于G,则的值为( )
A. B. C. D.
6.如图,正方形ABCD的面积为36,点E、F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF长为( )
A.2 B.3 C. D.
7.如图,A,B,C,D是边长为1的小正方形组成的6×5网格中的格点,连接BD交AC于点E,BC交网格线于点F,连接EF.给出4个结论:
①BF=EF;
②∠ABE=∠CEF;
③tan∠AED=2;
④CA CE=10.
其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
二.填空题(共11小题)
8.如图,正方形网格中,每一小格的边长为2.P、A、B均为格点.
(1)AP= ;
(2)点B到直线AP的距离是 ;
(3)∠APB= ;
(4)S△APB= .
9.如图,正方形纸片ABCD中,AB=6,G是BC的中点.将△ABG沿AG翻折至△AFG,延长GF交DC于点E,则DE的长等于 .
10.如图,正方形ABCD,AB=2,点E为AD上一动点,将三角形ABE沿BE折叠,点A落在点F处,连接DF并延长,与边AB交于点G,若点G为AB中点,则AE= .
11.如图,在平面直角坐标系中,已知点A(1,0),点B(0,﹣3),点C在x轴上,且点C在点A右方,连接AB,BC,若tan∠ABC,则点C的坐标为 .
12.如图,在边长为3的正方形ABCD中,点E是边AB上的点,且BE=2AE,过点E作DE的垂线交正方形外角∠CBG的平分线于点F,交边BC于点M,连接DF交边BC于点N,则MN的长为 .
13.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=1,将△ABC绕点A逆时针方向旋转90°,得到△AB′C′.连接BB′,交AC于点D,则的值为 .
14.如图,正方形ABCD的边长为,点E是CD的中点,BE与AC交于点M,F是AD上一点,连接BF分别交AC,AE于点G,H,且BF⊥AE,连接MH,则AH= ,MH= .
15.如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,BE=2,F是AB边上一点,将△CEF沿CF翻折,使点E的对应点G落在AD边上,连接EG交折痕CF于点H,则FH的长是 .
16.如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE,∠EAF=45°,则AF的长为 .
17.如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在点A′的位置,若OB,tan∠BOC,则点A′的坐标为 .
18.如图,已知正方形ABCD的边长为6,E为BC的中点,将△ABE沿直线AE折叠后,点B落在点F处,AF交对角线BD于点G,则FG的长是 .
“12345”模型巩固练习
一.选择题(共7小题)
题号 1 2 3 4 5 6 7
答案 B A C B C A B
一.选择题(共7小题)
1.如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,连接AB,BC,则∠ABC的度数为( )
A.30° B.45° C.60° D.75°
【分析】根据勾股定理即可得到AB,BC,AC的长度,进行判断即可.
【解答】解:根据勾股定理可以得到:AC=BC,AB=2.
∵())2+()2=(2)2.
∴AC2+BC2=AB2.
∴△ABC是等腰直角三角形.
∴∠ABC=45°.
故选:B.
【点评】本题考查了勾股定理,判断△ABC是等腰直角三角形是解决本题的关键.
2.如图,矩形ABCD中,AB=3,BC=4,以点B为圆心,适当长为半径画弧,分别交BC,BD于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线BP,过点C作BP的垂线分别交BD,AD于点M,N,则CN的长为( )
A. B. C.4 D.5
【分析】先证明三角形全等,再根据勾股定理求解.
【解答】解:设CN交BP于点Q,
在矩形ABCD中,∠BCD=∠ADC=90°,AD∥BC,
∵AB=3,BC=4,
∴BD=5,
由作图得:BP平分∠CBD,
∴∠DBP=∠CBP,
∵过点C作BP的垂线分别交BD,AD于点M,N,
∴∠MQB=∠CQB=90°,
∵BQ=BQ,
∴△BQM≌△BQC(ASA),
∴BM=BC=4,∠CMB=∠MCB,
∴DM=BD﹣BM=1,
∵AD∥BC,
∴∠DNC=∠NCB,
∵∠DMN=∠CMB,
∴∠DNC=∠NMD,
∴DN=DM=1,
∴NC,
故选:A.
【点评】本题考查了作图﹣基本作图,掌握三角形全等是性质及勾股定理是解题的关键.
3.如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是( )
A. B.1 C. D.
【分析】连接AF,由矩形的性质得出∠B=∠C=90°,CD=AB=2,BC=AD=3,证出AB=FC,BF=CE,由SAS证明△ABF≌△FCE,得出∠BAF=∠CFE,AF=FE,证△AEF是等腰直角三角形,得出∠AEF=45°,即可得出答案.
【解答】解:连接AF,如图所示:
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD=AB=2,BC=AD=3,
∵FC=2BF,
∴BF=1,FC=2,
∴AB=FC,
∵E是CD的中点,
∴CECD=1,
∴BF=CE,
在△ABF和△FCE中,
,
∴△ABF≌△FCE(SAS),
∴∠BAF=∠CFE,AF=FE,
∵∠BAF+∠AFB=90°,
∴∠CFE+∠AFB=90°,
∴∠AFE=180°﹣90°=90°,
∴△AEF是等腰直角三角形,
∴∠AEF=45°,
∴cos∠AEF;
故选:C.
【点评】本题考查了矩形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、三角函数等知识;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.
4.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图①),后人称之为“赵爽弦图”,流传至今,如图①是用四个全等的直角三角形拼成一个正方形,利用面积法可以证明勾股定理.如图2连接EG并延长交AD的延长线于点M,如,则的值为( )
A.2 B. C. D.1.4
【分析】在Rt△DGM中,根据,设DG=x,DM=2x,从而利用勾股定理求出GM,再设HD=y,根据题意可得AE=HD=y,AH=DG=x,从而求出AM,然后在Rt△AEM中,利用锐角三角函数的定义可得,从而求出y=3x,最后在Rt△HDG中,利用勾股定理求出HG,进行计算即可解答.
【解答】解:tanM,
∴,
∴设DG=x,DM=2x,
∴,
设HD=y,
由题意得:△AEH≌△DHG,
∴AE=HD=y,AH=DG=x,
,
∴,
∴3x+y=2y,
∴y=3x,
∴DH=y=3x,
∴,
∴,
故选:B.
【点评】本题考查了勾股定理的证明,解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.
5.如图,正方形ABCD中,E是AD中点,连接AC,作DF⊥CE交AB于F,交CE于P,交AC于H,延长DF交CB延长线于G,则的值为( )
A. B. C. D.
【分析】先证明△ADF≌△DCE,得AF=DEAB,根据AD∥BC证明△ADF∽△BGF,△ADH∽△CGH,△DEP∽△GCP,列比例式可求得:PH和GH的长,从而得结论.
【解答】解:∵四边形ABCD是正方形,
∴AD=CD,∠BAD=∠ADC=90°,
∴∠ADF+∠CDP=90°,
∵DF⊥CE,
∴∠CPD=90°,
∴∠DCE+∠CDP=90°,
∴∠ADF=∠DCE,
∴△ADF≌△DCE(ASA),
∴AF=DE,
∵点E是AD的中点,
∴DEAD,
∴AFAB,
∵四边形ABCD是正方形,
∴AD∥BC,
∴△ADF∽△BGF,△ADH∽△CGH,△DEP∽△GCP,
∴1,,,
设PD=a,则PG=4a,
∴DHa,GHa
∴PH=DH﹣PDa﹣aa
∴.
故选:C.
【点评】本题考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解决问题的关键是弄清比例之间的数量关系.
6.如图,正方形ABCD的面积为36,点E、F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF长为( )
A.2 B.3 C. D.
【分析】首先延长FD到G,使DG=BE,利用正方形的性质得∠B=∠CDF=∠CDG=90°,CB=CD;利用SAS定理得△BCE≌△DCG,利用全等三角形的性质易得△GCF≌△ECF,利用勾股定理可得AE=3,设AF=x,利用GF=EF,解得x,利用勾股定理可得CF.
【解答】解:∵正方形ABCD的面积为36,
∴BC=AB=6,
如图,延长FD到G,使DG=BE;
连接CG、EF;
∵四边形ABCD为正方形,
在△BCE与△DCG中,,
∴△BCE≌△DCG(SAS),
∴CG=CE,∠DCG=∠BCE,
∴∠GCF=45°,
在△GCF与△ECF中,,
∴△GCF≌△ECF(SAS),
∴GF=EF,
∵CE=3,CB=6,
∴BE=3,
∴AE=3,
设AF=x,则DF=6﹣x,GF=3+(6﹣x)=9﹣x,
∴EF,
∴(9﹣x)2=9+x2,
∴x=4,
即AF=4,
∴DF=6﹣4=2,
∴CF2,
故选:A.
【点评】本题主要考查了正方形的性质,全等三角形的判定及性质,勾股定理等,构建全等三角形,利用方程思想是解答此题的关键.
7.如图,A,B,C,D是边长为1的小正方形组成的6×5网格中的格点,连接BD交AC于点E,BC交网格线于点F,连接EF.给出4个结论:
①BF=EF;
②∠ABE=∠CEF;
③tan∠AED=2;
④CA CE=10.
其中正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
【分析】连接CD,利用全等三角形的判定与性质得到∠DCB=90°,则△CDB为等腰直角三角形;利用角平分线的性质定理和平行线分线段成比例定理得到2,则EF∥CD,利用平行线的性质得到∠FEB=∠CDB=45°,则△FEB为等腰直角三角形,则得①的结论正确;利用三角形的内角和定理得到∠ABE=∠DCE,利用两直线平行,内错角相等得到∠CEF=∠DCE,则②的结论正确;利用三角形的外交的性质得到∠AED=∠CBA,在Rt△CHB中,利用直角三角形的边角关系定理得到tan∠CBA3,则得③的结论不正确;利用相似三角形的判定与性质,列出比例式计算,则得④的结论正确.
【解答】解:连接CD,G,H为格点,如图,
由题意得:AD=2,AB=4,CD=CB,∠DAC=∠BAC=45°.
在△DCG和△CBH中,
,
∴△DCG≌△CBH(SAS),
∴∠DCG=∠CBH,
∵∠CBH+∠BCH=90°,
∴∠DCG+∠BCH=90°,
∴∠DCB=90°,
∴△DCB为等腰直角三角形,
∴∠CDB=∠CBD=45°.
∵∠DAC=∠BAC=45°,
∴2,
∵FG∥BH,
∴2,
∴,
∴EF∥CD,
∴∠FEB=∠CDB=45°,
∴∠FEB=∠CBD=45°,
∴BF=EF.
∴①的结论正确;
∵∠CAB=∠CDB=45°,∠AEB=∠DEC,
∴∠ABE=∠DCE.
∵EF∥CD,
∴∠CEF=∠DCE,
∴∠ABE=∠CEF.
∴②的结论正确;
∵∠AED=∠EAB+∠ABE=45°+∠ABE,∠CBA=∠CBD+∠ABE=45°+∠ABE,
∴∠AED=∠CBA,
在Rt△CHB中,
tan∠CBA3,
∴tan∠AED=tan∠CBA=3,
∴③的结论不正确;
∵∠CBD=∠CAB=45°,∠ECB=∠BCA,
∴△BCE∽△ACB,
∴,
∴CA CE=CB210,
∴④的结论正确.
综上,正确的结论有:①②④.
故选:B.
【点评】本题主要考查了解直角三角形,直角三角形的性质,勾股定理,相似三角形的判定与性质平行线的判定与性质,平行线分线段成比例定理,等腰直角三角形的判定与性质,本题是网格题,熟练掌握网格的特性是解题的关键.
二.填空题(共11小题)
8.如图,正方形网格中,每一小格的边长为2.P、A、B均为格点.
(1)AP= 2 ;
(2)点B到直线AP的距离是 2 ;
(3)∠APB= 135° ;
(4)S△APB= 10 .
【分析】(1)用勾股定理求解即可;
(2)延长AP得格点C,连接BC,PC,证∠BCP=90°,则点B到直线AP的距离是线段BC的长,再由勾股定理求出BC的长即可;
(3)由(2)问图可证△BPC是等腰直角三角形,从而得∠BPC=45°,即可由∠APB=180°﹣∠BPC求解;
(4)根据三角形面积公式计算即可求解.
【解答】解:(1)1×2=2,
2×2=4,
AP2.
故答案为:2;
(2)延长AP得格点C,连接BC,PC,如图,
由图可得:PE=CD,CE=BD,∠PEC=∠BDC=90°,
∴△PEC≌△CDB(SAS),
∴∠PCE=∠CBD,
∴∠DCB+∠CBD=90°,
∴∠DCB+∠PCE=90°,
∴∠PCB=90°,
∴BC⊥AP,
∴点B到直线AP的距离是线段BC的长,
∴BC2.
故答案为:2;
(3)由(2)知△PEC≌△CDB(SAS),∠PCB=90°,
∴BC=PC,
∴△BPC是等腰直角三角形,
∴∠BPC=45°,
∴∠APB=180°﹣∠BPC=135°.
故答案为:135°;
(4)5×2=10,
10×2÷2=10.
故S△APB=10.
故答案为:10.
【点评】本题考查勾股定理,点到直线的距离,全等三角形的判定与性质,等腰直角三角形,熟练掌握在网格图用勾股定理求线段长是解题的关键.
9.如图,正方形纸片ABCD中,AB=6,G是BC的中点.将△ABG沿AG翻折至△AFG,延长GF交DC于点E,则DE的长等于 2 .
【分析】根据翻折变换的性质和正方形的性质可证Rt△AFE≌Rt△ADE;在直角△ECG中,根据勾股定理即可求出DE的长.
【解答】解:如图,连接AE,
∵AB=AD=AF,∠D=∠AFE=90°,
在Rt△AFE和Rt△ADE中,
∴Rt△AFE≌Rt△ADE,
∴EF=DE,
设DE=FE=x,则EC=6﹣x.
∵G为BC中点,BC=6,
∴CG=3,
在Rt△ECG中,根据勾股定理,得:(6﹣x)2+32=(x+3)2,
解得x=2.
则DE=2.
故答案为2.
【点评】本题考查了翻折变换,解题的关键是掌握翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理.
10.如图,正方形ABCD,AB=2,点E为AD上一动点,将三角形ABE沿BE折叠,点A落在点F处,连接DF并延长,与边AB交于点G,若点G为AB中点,则AE= .
【分析】过点F作MN∥AB,分别交AD,BC于点M,N,根据点G为AB中点可得AG=1,不难推出四边形ABNM为矩形,△DMF∽△DAG,则,设MF=x,则DM=2x,AM=2﹣2x,NF=2﹣x,BN=AM=2﹣2x,根据折叠的性质可得AE=EF,AB=BF=2,根据勾股定理得BF2=BN2+NF2,以此得出,,设AE=y,则EF=y,EM=AD﹣DM﹣AE=2,再根据勾股定理得EF2=EM2+MF2,以此列出方程求解即可.
【解答】解:过点F作MN∥AB,分别交AD,BC于点M,N,如图,
,
∵四边形ABCD为正方形,
∴∠A=90°,AB=AD=2,四边形ABNM为矩形,
∴AM=BN,AB=MN=2,
∵点G为AB中点,
∴1,
∵MN∥AB,
∴△DMF∽△DAG,
∴,
即DM=2MF,
设MF=x,则DM=2x,AM=2﹣2x,NF=2﹣x,
∴BN=AM=2﹣2x,
根据折叠的性质得,AE=EF,AB=BF=2,
在Rt△BNF中,
根据勾股定理得,BF2=BN2+NF2,
∴22=(2﹣2x)2+(2﹣x)2,
整理得,5x2﹣12x+4=0,
解得:或2(舍去),
∴,,
设AE=y,则EF=y,EM=AD﹣DM﹣AE=2,
在Rt△EMF中,
由勾股定理得,EF2=EM2+MF2,
∴,
∴y,
∴AE.
故答案为:.
【点评】本题主要考查折叠的性质、相似三角形的判定与性质、勾股定理、正方形的性质,正确作出辅助线,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案是解题关键.
11.如图,在平面直角坐标系中,已知点A(1,0),点B(0,﹣3),点C在x轴上,且点C在点A右方,连接AB,BC,若tan∠ABC,则点C的坐标为 (,0) .
【分析】设C(a,0),结合A,B两点的坐标利用两点间的距离可得OA=1,AC=a﹣1,OB=3,BC,通过解直角三角形可得∠OBA=∠ABC,过C点作CD∥y轴交BA的延长线于点D,利用平行线的性质可得△OBA∽△CDA,∠ABC=∠D,列比例式再代入计算可求解a值,进而可求解.
【解答】解:设C(a,0),
∴OC=a,
∵点A(1,0),点B(0,﹣3),
∴OA=1,AC=a﹣1,OB=3,BC,
在Rt△OAB中,tan∠OBA,tan∠ABC,
∴∠OBA=∠ABC,
过C点作CD∥y轴交BA的延长线于点D,
∴∠OBA=∠D,∠AOB=∠ACD,
∴△OBA∽△CDA,∠ABC=∠D,
∴,CD=BC,
∴,
∴,
解得a=0(舍去)或a,
∴C(,0),
故答案为:(,0).
【点评】本题主要考查坐标与图形的性质,相似三角形的判定与性质,等腰三角形的性质,平行线的性质,两点间的距离等知识的综合运用,作适当的辅助线是解题的关键.
12.如图,在边长为3的正方形ABCD中,点E是边AB上的点,且BE=2AE,过点E作DE的垂线交正方形外角∠CBG的平分线于点F,交边BC于点M,连接DF交边BC于点N,则MN的长为 .
【分析】根据正方形的性质、相似三角形的判定和性质,可以求得CN和BM的长,然后根据BC=3,即可求得MN的长.
【解答】解:作FH⊥BG交于点H,作FK⊥BC于点K,
∵BF平分∠CBG,∠KBH=90°,
∴四边形BHFK是正方形,
∵DE⊥EF,∠EHF=90°,
∴∠DEA+∠FEH=90°,∠EFH+∠FEH=90°,
∴∠DEA=∠EFH,
∵∠A=∠EHF=90°,
∴△DAE∽△EHF,
∴,
∵正方形ABCD的边长为3,BE=2AE,
∴AE=1,BE=2,
设FH=a,则BH=a,
∴,
解得a=1;
∵FK⊥CB,DC⊥CB,
∴△DCN∽△FKN,
∴,
∵BC=3,BK=1,
∴CK=2,
设CN=b,则NK=2﹣b,
∴,
解得b,
即CN,
∵∠A=∠EBM,∠AED=∠BME,
∴△ADE∽△BEM,
∴,
∴,
解得BM,
∴MN=BC﹣CN﹣BM=3.
故答案为:.
【点评】本题考查正方形的性质、相似三角形的判定和性质,解答本题的关键是明确题意,利用数形结合的思想解答.
13.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=1,将△ABC绕点A逆时针方向旋转90°,得到△AB′C′.连接BB′,交AC于点D,则的值为 5 .
【分析】过点D作DF⊥AB于点F,利用勾股定理求得 AB,根据旋转的性质可证△ABB'、△DFB 是等腰直角三角形,可得DF=BF,再由S△ADBBCDF×AB,ADDF,证明△AFD∽△ACB,可得 ,即AF=3DF,再由 ,求得 ,从而求得 ,,即可求解.
【解答】解:过点D作DF⊥AB于点F,
,
∵∠ACB=90°,AC=3,BC=1,,
∵将△ABC绕点A逆时针方向旋转 90° 得到△AB'C',,∠BAB'=90°,
∴△ABB'是等腰直角三角形,
∴∠ABB'=45°
∵DF⊥AB,∠DFB=90°,
∴△DFB是等腰直角三角形,
∴DF=BF,
S△DBABC×ADDF×AB,即 ,
∵∠C=∠AFD=90°,∠CAB=∠FAD,
∴△AFD∽△ACB,
∴,
即AF=3DF,
又∵,
∴,
∴,
∴,
∴5,
故答案为:5.
【点评】本题考查旋转的性质、等腰三角形的判定与性质、相似三角形的判定与性质、三角形的面积,则 练掌握相关知识是解题的关键.
14.如图,正方形ABCD的边长为,点E是CD的中点,BE与AC交于点M,F是AD上一点,连接BF分别交AC,AE于点G,H,且BF⊥AE,连接MH,则AH= 2 ,MH= .
【分析】先求出AE=5,证△DAE和△ABF全等得DE=AF,AE=BF=5,再证△AFH∽△ADE,利用相似三角形的性质可得AH的长;过点M作MN⊥AE于点N,先求出AE=BE=5,EH=3,BH=4,证△MEC∽△MBA得ME:MB=CE:AB=1:2,进而得ME:EB=1:3,再证△MNE∽△BHE,利用相似三角形的性质得MN,EN=1,进而得HN=2,最后在Rt△MHN中,由勾股定理可求出MH.
【解答】解:∵四边形ABCD为正方形,且边长为,
∴AB=BC=CD=DA,∠BAD=∠D=90°,AB∥CD,
∵点E为CD的中点,
∴DE=CE,
在Rt△ADE中,AD,DE,
由勾股定理得:,
∵∠BAD=90°,BF⊥AE,
∴∠BAH+∠DAE=90°,∠ABF+∠BAH=90°,
∴∠DAE=∠ABF,
在△DAE和△ABF中,
,
∴△DAE≌△ABF(SAS),
∴DE=AF,AE=BF=5,
∵BF⊥AE,∠D=90°,
∴∠AHF=∠D=90°,
又∠HAF=∠DAE,
∴△AFH∽△ADE,
∴AH:AD=AF:AE,
即:AH::5,
∴AH=2.
过点M作MN⊥AE于点N,如图:
在△ADE和△BCE中,
,
∴△ADE≌△BCE(SAS),
∴AE=BE=5,
∴EH=AE﹣AH=5﹣2=3,
在Rt△AHB中,AB,AH=2,
由勾股定理得:,
∵AB∥CD,
∴△MEC∽△MBA,
∴ME:MB=CE:AB,
即:ME:MB:2,
∴ME:MB=1:2,
∴ME:EB=1:3,
∵BF⊥AE,MN⊥AE,
∴MN∥BH,
∴△MNE∽△BHE,
∴MN:BH=EN:EH=ME:EB
∴MN:4=EN:3=1:3,
∴MN,EN=1,
∴HN=EH﹣EN=3﹣1=2,
在Rt△MHN中,MN,HN=2,
由勾股定理得:.
故答案为:2,.
【点评】此题主要考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,熟练掌握全等三角形的判定和性质,灵活运用相似三角形的性质和勾股定理进行计算是解答此题的关键.
15.如图,已知正方形ABCD的边长为4,E是AB边延长线上一点,BE=2,F是AB边上一点,将△CEF沿CF翻折,使点E的对应点G落在AD边上,连接EG交折痕CF于点H,则FH的长是 .
【分析】由正方形的性质得AB=AD=CD=CB=4,∠A=∠D=∠ABC=90°,则∠CBE=90°,由翻折得CG=CE,则DGBE=2,所以AG=2,AE=6,则EG2,因为CF垂直平分EG,所以GF=EF,由勾股定理得22+(6﹣EF)2=EF2,求得EF,即可根据2FH2=S△EFG,求得FH,于是得到问题的答案.
【解答】解:∵四边形ABCD是边长为4的正方形,
∴AB=AD=CD=CB=4,∠A=∠D=∠ABC=90°,
∴∠CBE=90°,
由翻折得CG=CE,
∴DGBE=2,
∴AG=AD﹣DG=4﹣2=2,AE=AB+BE=4+2=6,
∴EG2,
∵点G与点E关于直线CF对称,
∴CF垂直平分EG,
∴GF=EF,
∵AG2+AF2=GF2,且AF=6﹣EF,
∴22+(6﹣EF)2=EF2,
解得EF,
∵EG FHEF AG=S△EFG,
∴2FH2,
解得FH,
故答案为:.
【点评】此题重点考查正方形的性质、轴对称的性质、勾股定理、根据面积等式求线段的长度等知识与方法,求得DG=2是解题的关键.
16.如图,在矩形ABCD中,AB=2,BC=4,点E、F分别在BC、CD上,若AE,∠EAF=45°,则AF的长为 .
【分析】取AB的中点M,连接ME,在AD上截取ND=DF,设DF=DN=x,则NFx,再利用矩形的性质和已知条件证明△AME∽△FNA,利用相似三角形的性质:对应边的比值相等可求出x的值,在直角三角形ADF中利用勾股定理即可求出AF的长.
【解答】解:取AB的中点M,连接ME,在AD上截取ND=DF,设DF=DN=x,
∵四边形ABCD是矩形,
∴∠D=∠BAD=∠B=90°,AD=BC=4,
∴NFx,AN=4﹣x,
∵AB=2,
∴AM=BM=1,
∵AE,AB=2,
∴BE=1,
∴ME,
∵∠EAF=45°,
∴∠MAE+∠NAF=45°,
∵∠MAE+∠AEM=45°,
∴∠MEA=∠NAF,
∴△AME∽△FNA,
∴,
∴,
解得:x,
经检验,x是分式方程的解,
∴AF.
故答案为:.
【点评】本题考查了矩形的性质、相似三角形的判断和性质以及勾股定理的运用,正确添加辅助线构造相似三角形是解题的关键,
17.如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在点A′的位置,若OB,tan∠BOC,则点A′的坐标为 (,) .
【分析】过点A′作A′D⊥x轴于点D,根据题意首先求出AB、BC的长度;借助面积公式求出A′D、OD的长度,即可解决问题.
【解答】解:如图,过点A′作A′D⊥x轴于点D,
∵四边形ABCO为矩形,
∴∠AOC=∠OAB=∠OCB=90°,OA=BC,
∵OB,tan∠BOC,
∴OA=BC=1,OC=AB=2,
由折叠的性质得:A′O=AO=1,△ABO≌△EBO,
设A′D=x,OD=y;
由勾股定理得:x2+y2=1①,
由面积公式得:xy+22×1(x+2)(y+1)②;
联立①②并解得:x,y,
则点A′的坐标为(,).
故答案为:(,).
【点评】此题考查翻折变换,坐标与图形的性质;解决问题的关键是综合利用矩形的性质,勾股定理等几何知识点.
18.如图,已知正方形ABCD的边长为6,E为BC的中点,将△ABE沿直线AE折叠后,点B落在点F处,AF交对角线BD于点G,则FG的长是 .
【分析】延长AF,EF分别交CD于H,M,连接AM,根据折叠的性质得到AB=AF,∠ABE=∠AFE=90°,根据全等三角形的性质得到DM=FM,设DM=FM=x,则CM=6﹣x,EM=3+x,根据勾股定理得到DM=FM=2,根据相似三角形的判定和性质定理即可得到结论.
【解答】解:延长AF,EF分别交CD于H,M,连接AM,
∵四边形ABCD是正方形,
∴AB=AD,∠ABE=∠ADC=90°,
∵将△ABE沿直线AE折叠后,点B落在点F处,
∴AB=AF,∠ABE=∠AFE=90°,
∴∠ADM=∠AFM=90°,AF=AD,
∵AM=AM,
∴Rt△ADM≌Rt△AFM(HL),
∴DM=FM,
∵E为BC的中点,BC=CD=6,
∴CE=3,
设DM=FM=x,则CM=6﹣x,EM=3+x,
∵EM2=CM2+CE2,
∴(3+x)2=32+(6﹣x)2,
解得:x=2,
∴DM=FM=2,
∵∠MFH=∠ECM=90°,∠HMF=∠CME,
∴△MFH∽△MCE,
∴,
∴,
∴MH=2.5,FH=1.5,
∴AH=6+1.5=7.5,DH=4.5,
∵AB∥DH,
∴△AGB∽△HGD,
∴,
∴,
∴AG,
∴GF=AF﹣AG,
故答案为:.
【点评】本题考查了翻折变换(折叠问题),正方形的性质,全等三角形的判定和性质,勾股定理,相似三角形的判定和性质,正确的作出辅助线是解题的关键.
同课章节目录
