九年级数学上册沪科版 21.1 《二次函数》小节复习题(含答案)
文档属性
| 名称 | 九年级数学上册沪科版 21.1 《二次函数》小节复习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 100.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-11 20:53:35 | ||
图片预览




文档简介
21.1 《二次函数》小节复习题
【题型1 二次函数的识别】
1.下列函数中,属于二次函数的是( )
A. B.
C. D.
2.在圆的面积公式中,与的关系是( )
A.一次函数关系 B.正比例函数关系
C.反比例函数关系 D.二次函数关系
3.下列函数是二次函数的是( )
A. B.
C. D.
4.观察:①;②;③;④;⑤;⑥.这六个式子中,二次函数有 .(只填序号)
【题型2 根据二次函数的定义求参数】
1.若函数 是二次函数,那么m的值是( )
A.2 B.或3 C.3 D.
2.当 时,是二次函数.
3.若函数是关于x的二次函数,则m的取值范围是( )
A. B. C. D.
4.已知关于x的函数y=(m﹣1)xm+(3m+2)x+1是二次函数,则此解析式的一次项系数是( )
A.﹣1 B.8 C.﹣2 D.1
【题型3 二次函数的一般形式】
1.将二次函数化为一般形式后,正确的是( )
A. B.
C. D.
2.二次函数的一般式为 .
3.把函数化成的形式为 .
4.二次函数的一般形式是 .
【题型4 二次函数的各项系数】
1.把y=(3x-2)(x+3)化成一般形式后,一次项系数与常数项的和为 .
2.在二次函数中,二次项系数与一次项系数的和是 .
3.设a,b,c分别是二次函数y=﹣x2+3的二次项系数、一次项系数、常数项,则( )
A.a=﹣1,b=3,c=0 B.a=﹣1,b=0,c=3
C.a=﹣1,b=3,c=3 D.a=1,b=0,c=3
4.已知二次函数.
(1)将该函数表达式化为二次函数的一般形式;
(2)写出该二次函数的二次项系数、一次项系数和常数项.
【题型5 二次函数图象上点的坐标特征】
1.某车的刹车距离(m)与开始刹车时的速度(m/s)之间满足二次函数,若该车某次的刹车距离为m,则开始刹车时的速度为( )
A.4m/s B.5m/s C.8m/s D.10m/s
2.下列各点中,在二次函数图象上的点是( )
A. B. C. D.
3.关于的二次函数的图象过原点,则的值为( ).
A.1 B. C. D.0
4.如图,在期末体育测试中,小朱掷出的实心球的飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数,则小朱本次投掷实心球的成绩为( )
A.7m B.7.5m C.8m D.8.5m
【题型6 建立二次函数模型,列函数表达式(实际应用)】
1.某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个元.经市场调查发现,这种双肩包每天的销售量(个)与销售单价(元个)有如下关系:(,且为整数).设这种双肩包每天的销售利润为元.则与之间的函数关系式为 .
2.一部售价为5000元的手机,一年内连续两次降价,如果每次降价的百分率都是x,则两次降价后的价格y(元)与每次降价的百分率x之间的函数关系式是 .
3.已知有n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数为m,则m关于n的函数解析式为 .
4.某果园有棵枇杷树.每棵平均产量为千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵树接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量千克,若设增种棵枇杷树,投产后果园枇杷的总产量为千克,则与之间的函数关系式为 .
【题型7 建立二次函数模型,列函数表达式(几何图形)】
1.深高小学部饲养了两只萌萌的羊驼,建筑队在学校一边靠墙处,计划用15米长的铁栅栏围成三个相连的长方形羊驼草料仓库,仓库总面积为y平方米,为方便取物,在各个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门,若设米,则y关于x的函数关系式为( )
A. B.
C. D.
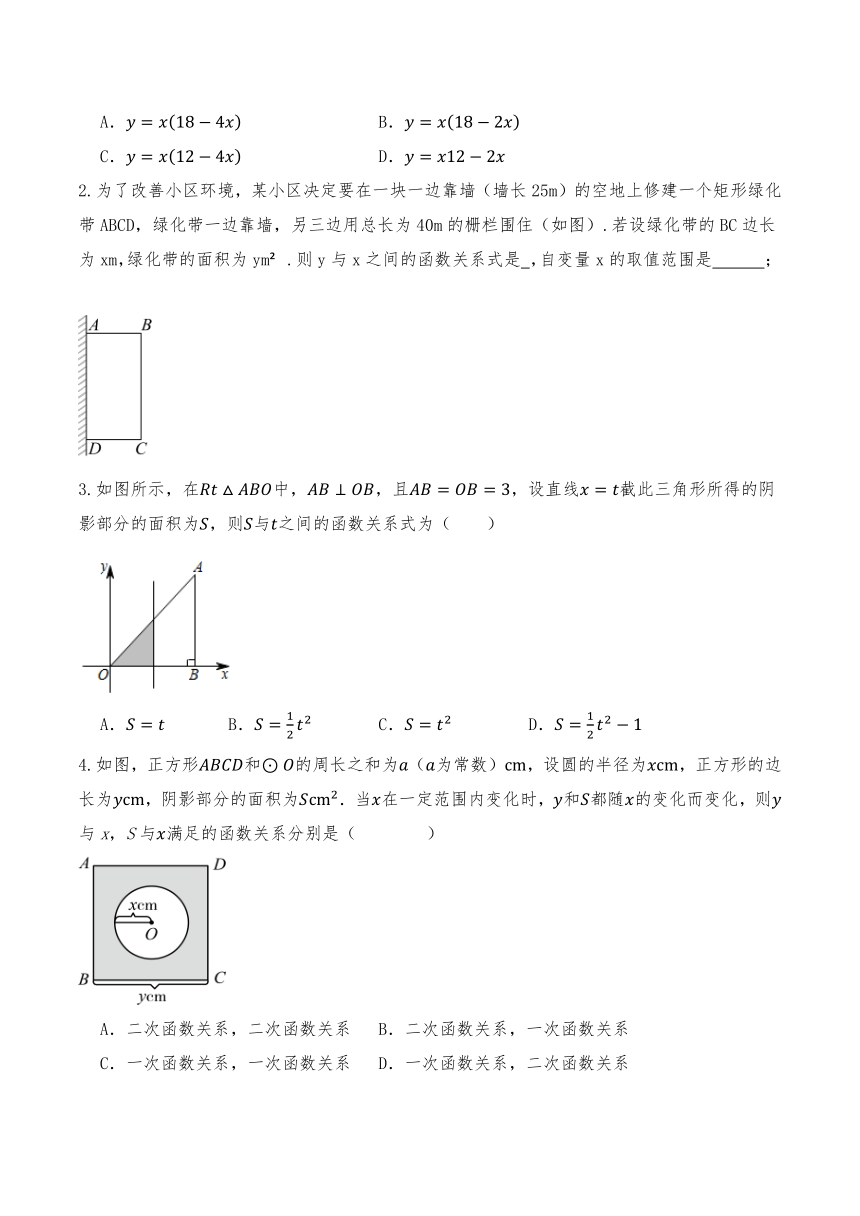
2.为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带的BC边长为xm,绿化带的面积为ym .则y与x之间的函数关系式是 ,自变量x的取值范围是 ;
3.如图所示,在中,,且,设直线截此三角形所得的阴影部分的面积为,则与之间的函数关系式为( )
A. B. C. D.
4.如图,正方形和的周长之和为(为常数),设圆的半径为,正方形的边长为,阴影部分的面积为.当在一定范围内变化时,和都随的变化而变化,则与x,S与满足的函数关系分别是( )
A.二次函数关系,二次函数关系 B.二次函数关系,一次函数关系
C.一次函数关系,一次函数关系 D.一次函数关系,二次函数关系
参考答案
【题型1 二次函数的识别】
1.C
【分析】判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成,,为常数,的形式,那么这个函数就是二次函数,否则就不是.
【详解】解:A.是一次函数,故不符合题意;
B.当时是一次函数,故不符合题意;
C.是二次函数,故符合题意;
D.是一次函数,故不符合题意
故选:C.
2.D
【分析】本题考查了二次函数的定义,根据二次函数的定义即可判断,解题的关键是正确理解:一般地形如(是常数,)的函数叫做二次函数.
【详解】解:圆的面积公式中,与的关系是二次函数关系,
故选:..
3.C
【分析】根据二次函数的定义判断即可.
此题主要考查了二次函数定义,解题的关键是掌握形如、、是常数,的函数,叫做二次函数.
【详解】解:、当时,该函数不是二次函数,故本选项不符合题意;
B、该函数分母含有字母,不是二次函数,故本选项不符合题意;
C、该函数是二次函数,故本选项符合题意;
D、该函数化简后没有二次项,是一次函数,故本选项不符合题意.
故选:.
4.①②③
【分析】本题主要考查的是二次函数的定义.熟练掌握二次函数的概念是解题的关键.形如 (a、b、c是常数,)的函数叫做二次函数.
根据二次函数的定义可得答案.
【详解】①,是二次函数;
②,是二次函数;
③,是二次函数;
④,不是二次函数;
⑤∵中不是整 式,∴不是二次函数;
⑥,不是二次函数.
∴①②③是二次函数.
故答案为:①②③.
【题型2 根据二次函数的定义求参数】
1.C
【分析】根据二次函数的定义:,进行计算即可.
【详解】解:由题意得:,解得:或;
又∵,解得:且,
∴.
故选C.
2.
【分析】本题考查二次函数的定义,根据二次函数的定义可得,,再求解即可.
【详解】解:由题意,得,,
解得,
即当时,是二次函数,
故答案为:.
3.B
【分析】本题考查了二次函数的定义,熟练掌握二次函数的一般式为是解本题的关键是解题的关键.根据二次函数的定义求解即可.
【详解】解:∵是关于x的二次函数,
∴,
解得:,
故选B.
4.B
【分析】根据二次函数的一般形式为,其中二次项系数a≠0,且二次项指数为2求解即可.
【详解】∵是二次函数,∴,即,∴此解析式的一次项系数是,故本题正确答案为B选项.
【题型3 二次函数的一般形式】
1.D
【分析】本题考查二次函数的一般式,根据整式乘法展开后合并同类项即可.
【详解】,
故选:D.
2.
【分析】二次函数的一般形式为,据此即可获得答案.
【详解】解:二次函数的一般式为.
故答案为:.
3.
【分析】把函数右边相乘展开合并成形式即可.
【详解】,则.
4.
【分析】直接利用乘法运算法则化成一般式.
【详解】y= 4(1+2x)(x 3)= 8x2+20x+12,
故答案为y= 8x2+20x+12.
【题型4 二次函数的各项系数】
1.1
【分析】先将其化为一般式,即可求出一次项系数和常数项,从而求出结论.
【详解】解:y=(3x-2)(x+3)=3x2+7x-6
∴一次项系数为7,常数项为-6
∴一次项系数与常数项的和为7+(-6)=1
故答案为:1.
2.
【分析】本题主要考查了二次函数的定义,根据二次函数的定义:一般地,形如(a、b、c是常数,)的函数,叫作二次函数.其中x、y是变量,a、b、c是常量,a是二次项系数,b是一次项系数,c是常数项;
由题意可得二次项系数是2,常数项是,再求和即可.
【详解】解:在二次函数中,
二次项系数为2, 一次项次数为,
∴二次项系数与一次项系数的和是:,
故答案为:.
3.B
【分析】根据二次函数的一般形式可得答案.
【详解】解:二次函数y=﹣x2+3的二次项系数是a=﹣1,一次项系数是b=0,常数项是c=3;
故选:B.
4.(1)解:
该二次函数的一般形式是;
(2)解:由(1)可得,该函数的二次项系数是,一次项系数是,常数项是4.
【题型5 二次函数图象上点的坐标特征】
1.D
【分析】本题实际是告知函数值求自变量的值,代入求解即可,另外实际问题中,负值舍去.
【详解】解:当刹车距离为m时,即可得,
代入二次函数解析式得:,
解得,(舍),
故开始刹车时的速度为m/s,
故选:D.
2.B
【分析】把选项坐标代入二次函数验证即可.
【详解】A. ,选项错误,不符合题意;
B. ,选项正确,符合题意;
C. ,选项错误,不符合题意;
D. ,选项错误,不符合题意.
故选:B.
3.A
【分析】本题考查二次函数的图象和性质,将代入二次函数解析式,得到关于a的方程,解方程即可,注意二次项系数不能为0.
【详解】解:∵二次函数的图象过原点,
∴,,
∴,
故选:A.
4.C
【分析】根据实心球落地时,高度y=0,把实际问题可理解为当y=0时,求x的值即可.
【详解】解:在中,令y=0得:
,
解得x=-2(舍去)或x=8,
∴小朱本次投掷实心球的成绩为8米,
故选:C.
【题型6 建立二次函数模型,列函数表达式(实际应用)】
1.
【分析】此题考查求二次函数解析式,根据销售总利润等于单件利润乘销售量计算解答.
【详解】解:,
故答案为:.
2.
【分析】本题主要考查了二次函数的实际应用,根据两次降价后的价格等于原价乘以(每次降价的百分率),列出函数关系式,即可求解.
【详解】解:依题意,每次降价的百分率都是x,两次降价后的价格y(元)与每次降价的百分率x之间的函数关系式是.
故答案为:.
3.
【分析】根据n个球队都要与除自己之外的球队个打一场,因此要打场,然而有重复一半的场次,即可求出函数关系式.
【详解】解:根据题意,得,
故答案为: .
4.
【分析】投产后果园枇杷的总产量=每棵树的产量×树的棵树=(40-减少的产量)×(100+增加的棵树),把相关数值代入即可求解.
【详解】∵每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量0.25千克,
∴每多种x棵树,投产后果园中所有的枇杷树平均每棵就会减少产量0.25x千克,
∴每棵树的产量为(40-0.25x)千克,
∵原来有100棵树,现在增加了x棵,
∴现在有(100+x)棵,
∴y=(100+x)(40-0.25x).
【题型7 建立二次函数模型,列函数表达式(几何图形)】
1.A
【分析】本题考查了根据实际问题列二次函数关系式,由铁栅栏的全长及的长,可得出平行于墙的一边长为米,再利用长方形的面积公式,即可找出y关于x的函数关系式.
【详解】解:铁栅栏的全长为15米,米,
平行于墙的一边长为米.
根据题意得:.
故选:A.
2.,
【分析】根据矩形的面积公式列出关于二次函数解析式;根据墙长、x、y所表示的实际意义来确定x的取值范围.
【详解】由题意得:
y=x = x2+20x,自变量x的取值范围是0<x≤25.
故答案是:y= x2+20x, 0<x≤25
3.B
【分析】中,,且,可得;再由平行线的性质得出,即,进而证明,最后根据三角形的面积公式,求出与之间的函数关系式.
【详解】解:如图所示,
∵中,,且,
∴,
∵,
∴,
∴,
∴,
∴,
∴
,
即:.
故选:B.
4.D
【分析】根据圆的周长公式和正方形的周长公式先得到,再根据得到,由此即可得到答案.
【详解】解:∵正方形和的周长之和为,圆的半径为,正方形的边长为,
∴,
∴,
∵,
∴,
∴y与x,S与x满足的函数关系分别是一次函数关系,二次函数关系,
故选:D.
【题型1 二次函数的识别】
1.下列函数中,属于二次函数的是( )
A. B.
C. D.
2.在圆的面积公式中,与的关系是( )
A.一次函数关系 B.正比例函数关系
C.反比例函数关系 D.二次函数关系
3.下列函数是二次函数的是( )
A. B.
C. D.
4.观察:①;②;③;④;⑤;⑥.这六个式子中,二次函数有 .(只填序号)
【题型2 根据二次函数的定义求参数】
1.若函数 是二次函数,那么m的值是( )
A.2 B.或3 C.3 D.
2.当 时,是二次函数.
3.若函数是关于x的二次函数,则m的取值范围是( )
A. B. C. D.
4.已知关于x的函数y=(m﹣1)xm+(3m+2)x+1是二次函数,则此解析式的一次项系数是( )
A.﹣1 B.8 C.﹣2 D.1
【题型3 二次函数的一般形式】
1.将二次函数化为一般形式后,正确的是( )
A. B.
C. D.
2.二次函数的一般式为 .
3.把函数化成的形式为 .
4.二次函数的一般形式是 .
【题型4 二次函数的各项系数】
1.把y=(3x-2)(x+3)化成一般形式后,一次项系数与常数项的和为 .
2.在二次函数中,二次项系数与一次项系数的和是 .
3.设a,b,c分别是二次函数y=﹣x2+3的二次项系数、一次项系数、常数项,则( )
A.a=﹣1,b=3,c=0 B.a=﹣1,b=0,c=3
C.a=﹣1,b=3,c=3 D.a=1,b=0,c=3
4.已知二次函数.
(1)将该函数表达式化为二次函数的一般形式;
(2)写出该二次函数的二次项系数、一次项系数和常数项.
【题型5 二次函数图象上点的坐标特征】
1.某车的刹车距离(m)与开始刹车时的速度(m/s)之间满足二次函数,若该车某次的刹车距离为m,则开始刹车时的速度为( )
A.4m/s B.5m/s C.8m/s D.10m/s
2.下列各点中,在二次函数图象上的点是( )
A. B. C. D.
3.关于的二次函数的图象过原点,则的值为( ).
A.1 B. C. D.0
4.如图,在期末体育测试中,小朱掷出的实心球的飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数,则小朱本次投掷实心球的成绩为( )
A.7m B.7.5m C.8m D.8.5m
【题型6 建立二次函数模型,列函数表达式(实际应用)】
1.某商店经销一种学生用双肩包,已知这种双肩包的成本价为每个元.经市场调查发现,这种双肩包每天的销售量(个)与销售单价(元个)有如下关系:(,且为整数).设这种双肩包每天的销售利润为元.则与之间的函数关系式为 .
2.一部售价为5000元的手机,一年内连续两次降价,如果每次降价的百分率都是x,则两次降价后的价格y(元)与每次降价的百分率x之间的函数关系式是 .
3.已知有n个球队参加比赛,每两队之间进行一场比赛,比赛的场次数为m,则m关于n的函数解析式为 .
4.某果园有棵枇杷树.每棵平均产量为千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵树接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量千克,若设增种棵枇杷树,投产后果园枇杷的总产量为千克,则与之间的函数关系式为 .
【题型7 建立二次函数模型,列函数表达式(几何图形)】
1.深高小学部饲养了两只萌萌的羊驼,建筑队在学校一边靠墙处,计划用15米长的铁栅栏围成三个相连的长方形羊驼草料仓库,仓库总面积为y平方米,为方便取物,在各个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门,若设米,则y关于x的函数关系式为( )
A. B.
C. D.
2.为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带的BC边长为xm,绿化带的面积为ym .则y与x之间的函数关系式是 ,自变量x的取值范围是 ;
3.如图所示,在中,,且,设直线截此三角形所得的阴影部分的面积为,则与之间的函数关系式为( )
A. B. C. D.
4.如图,正方形和的周长之和为(为常数),设圆的半径为,正方形的边长为,阴影部分的面积为.当在一定范围内变化时,和都随的变化而变化,则与x,S与满足的函数关系分别是( )
A.二次函数关系,二次函数关系 B.二次函数关系,一次函数关系
C.一次函数关系,一次函数关系 D.一次函数关系,二次函数关系
参考答案
【题型1 二次函数的识别】
1.C
【分析】判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成,,为常数,的形式,那么这个函数就是二次函数,否则就不是.
【详解】解:A.是一次函数,故不符合题意;
B.当时是一次函数,故不符合题意;
C.是二次函数,故符合题意;
D.是一次函数,故不符合题意
故选:C.
2.D
【分析】本题考查了二次函数的定义,根据二次函数的定义即可判断,解题的关键是正确理解:一般地形如(是常数,)的函数叫做二次函数.
【详解】解:圆的面积公式中,与的关系是二次函数关系,
故选:..
3.C
【分析】根据二次函数的定义判断即可.
此题主要考查了二次函数定义,解题的关键是掌握形如、、是常数,的函数,叫做二次函数.
【详解】解:、当时,该函数不是二次函数,故本选项不符合题意;
B、该函数分母含有字母,不是二次函数,故本选项不符合题意;
C、该函数是二次函数,故本选项符合题意;
D、该函数化简后没有二次项,是一次函数,故本选项不符合题意.
故选:.
4.①②③
【分析】本题主要考查的是二次函数的定义.熟练掌握二次函数的概念是解题的关键.形如 (a、b、c是常数,)的函数叫做二次函数.
根据二次函数的定义可得答案.
【详解】①,是二次函数;
②,是二次函数;
③,是二次函数;
④,不是二次函数;
⑤∵中不是整 式,∴不是二次函数;
⑥,不是二次函数.
∴①②③是二次函数.
故答案为:①②③.
【题型2 根据二次函数的定义求参数】
1.C
【分析】根据二次函数的定义:,进行计算即可.
【详解】解:由题意得:,解得:或;
又∵,解得:且,
∴.
故选C.
2.
【分析】本题考查二次函数的定义,根据二次函数的定义可得,,再求解即可.
【详解】解:由题意,得,,
解得,
即当时,是二次函数,
故答案为:.
3.B
【分析】本题考查了二次函数的定义,熟练掌握二次函数的一般式为是解本题的关键是解题的关键.根据二次函数的定义求解即可.
【详解】解:∵是关于x的二次函数,
∴,
解得:,
故选B.
4.B
【分析】根据二次函数的一般形式为,其中二次项系数a≠0,且二次项指数为2求解即可.
【详解】∵是二次函数,∴,即,∴此解析式的一次项系数是,故本题正确答案为B选项.
【题型3 二次函数的一般形式】
1.D
【分析】本题考查二次函数的一般式,根据整式乘法展开后合并同类项即可.
【详解】,
故选:D.
2.
【分析】二次函数的一般形式为,据此即可获得答案.
【详解】解:二次函数的一般式为.
故答案为:.
3.
【分析】把函数右边相乘展开合并成形式即可.
【详解】,则.
4.
【分析】直接利用乘法运算法则化成一般式.
【详解】y= 4(1+2x)(x 3)= 8x2+20x+12,
故答案为y= 8x2+20x+12.
【题型4 二次函数的各项系数】
1.1
【分析】先将其化为一般式,即可求出一次项系数和常数项,从而求出结论.
【详解】解:y=(3x-2)(x+3)=3x2+7x-6
∴一次项系数为7,常数项为-6
∴一次项系数与常数项的和为7+(-6)=1
故答案为:1.
2.
【分析】本题主要考查了二次函数的定义,根据二次函数的定义:一般地,形如(a、b、c是常数,)的函数,叫作二次函数.其中x、y是变量,a、b、c是常量,a是二次项系数,b是一次项系数,c是常数项;
由题意可得二次项系数是2,常数项是,再求和即可.
【详解】解:在二次函数中,
二次项系数为2, 一次项次数为,
∴二次项系数与一次项系数的和是:,
故答案为:.
3.B
【分析】根据二次函数的一般形式可得答案.
【详解】解:二次函数y=﹣x2+3的二次项系数是a=﹣1,一次项系数是b=0,常数项是c=3;
故选:B.
4.(1)解:
该二次函数的一般形式是;
(2)解:由(1)可得,该函数的二次项系数是,一次项系数是,常数项是4.
【题型5 二次函数图象上点的坐标特征】
1.D
【分析】本题实际是告知函数值求自变量的值,代入求解即可,另外实际问题中,负值舍去.
【详解】解:当刹车距离为m时,即可得,
代入二次函数解析式得:,
解得,(舍),
故开始刹车时的速度为m/s,
故选:D.
2.B
【分析】把选项坐标代入二次函数验证即可.
【详解】A. ,选项错误,不符合题意;
B. ,选项正确,符合题意;
C. ,选项错误,不符合题意;
D. ,选项错误,不符合题意.
故选:B.
3.A
【分析】本题考查二次函数的图象和性质,将代入二次函数解析式,得到关于a的方程,解方程即可,注意二次项系数不能为0.
【详解】解:∵二次函数的图象过原点,
∴,,
∴,
故选:A.
4.C
【分析】根据实心球落地时,高度y=0,把实际问题可理解为当y=0时,求x的值即可.
【详解】解:在中,令y=0得:
,
解得x=-2(舍去)或x=8,
∴小朱本次投掷实心球的成绩为8米,
故选:C.
【题型6 建立二次函数模型,列函数表达式(实际应用)】
1.
【分析】此题考查求二次函数解析式,根据销售总利润等于单件利润乘销售量计算解答.
【详解】解:,
故答案为:.
2.
【分析】本题主要考查了二次函数的实际应用,根据两次降价后的价格等于原价乘以(每次降价的百分率),列出函数关系式,即可求解.
【详解】解:依题意,每次降价的百分率都是x,两次降价后的价格y(元)与每次降价的百分率x之间的函数关系式是.
故答案为:.
3.
【分析】根据n个球队都要与除自己之外的球队个打一场,因此要打场,然而有重复一半的场次,即可求出函数关系式.
【详解】解:根据题意,得,
故答案为: .
4.
【分析】投产后果园枇杷的总产量=每棵树的产量×树的棵树=(40-减少的产量)×(100+增加的棵树),把相关数值代入即可求解.
【详解】∵每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量0.25千克,
∴每多种x棵树,投产后果园中所有的枇杷树平均每棵就会减少产量0.25x千克,
∴每棵树的产量为(40-0.25x)千克,
∵原来有100棵树,现在增加了x棵,
∴现在有(100+x)棵,
∴y=(100+x)(40-0.25x).
【题型7 建立二次函数模型,列函数表达式(几何图形)】
1.A
【分析】本题考查了根据实际问题列二次函数关系式,由铁栅栏的全长及的长,可得出平行于墙的一边长为米,再利用长方形的面积公式,即可找出y关于x的函数关系式.
【详解】解:铁栅栏的全长为15米,米,
平行于墙的一边长为米.
根据题意得:.
故选:A.
2.,
【分析】根据矩形的面积公式列出关于二次函数解析式;根据墙长、x、y所表示的实际意义来确定x的取值范围.
【详解】由题意得:
y=x = x2+20x,自变量x的取值范围是0<x≤25.
故答案是:y= x2+20x, 0<x≤25
3.B
【分析】中,,且,可得;再由平行线的性质得出,即,进而证明,最后根据三角形的面积公式,求出与之间的函数关系式.
【详解】解:如图所示,
∵中,,且,
∴,
∵,
∴,
∴,
∴,
∴,
∴
,
即:.
故选:B.
4.D
【分析】根据圆的周长公式和正方形的周长公式先得到,再根据得到,由此即可得到答案.
【详解】解:∵正方形和的周长之和为,圆的半径为,正方形的边长为,
∴,
∴,
∵,
∴,
∴y与x,S与x满足的函数关系分别是一次函数关系,二次函数关系,
故选:D.
