28.2解直角三角形(1)
文档属性
| 名称 | 28.2解直角三角形(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 41.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-01 00:00:00 | ||
图片预览

文档简介
第四课时 28.2解直角三角形(1)
一、学习目标
使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形
二、自学提纲:
1.在三角形中共有几个元素?
2.直角三角形ABC中,∠C=90°,那么剩下的
a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
以上三点正是解直角三角形的依据.
思考:在直角三角形的五个元素中,至少知道多少元素才能求出其余的元素
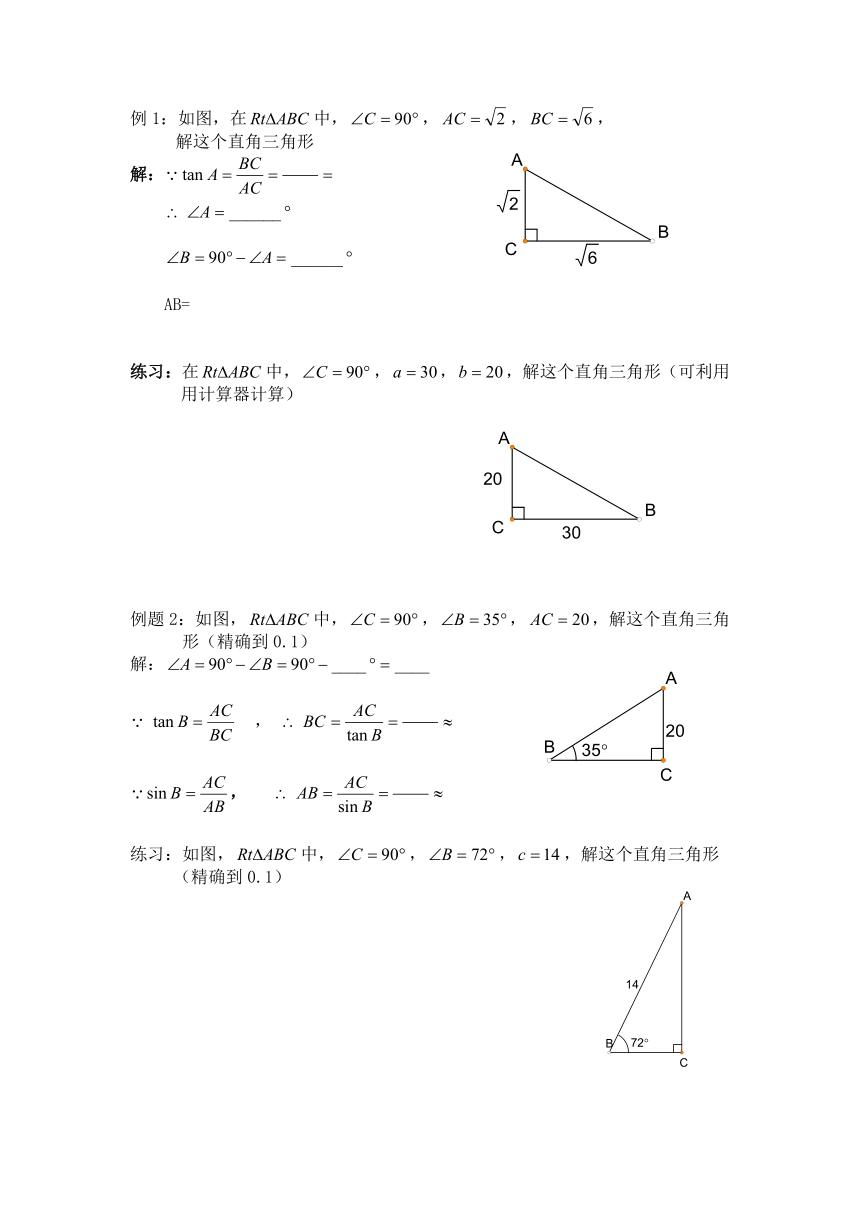
例1:如图,在中,,,,
解这个直角三角形
解:
AB=
练习:在中,,,,解这个直角三角形(可利用用计算器计算)
例题2:如图,中,,,,解这个直角三角形(精确到0.1)
解:
,
,
练习:如图,中,,,,解这个直角三角形
(精确到0.1)
A组:
1、如图中,, c= 8,∠A=60°,请你解这个直角三角形。
解:
BC=
2、如图中,,a=3, ∠A=30°,请你解这个直角三角形。
3、如图中,,a=6,b=2,请你解这个直角三角形
4、如图中,,c=,b=3,求a、A
B组 :
1、已知α为锐角,tanα=,则cosα等于( )
A. B. C. D.
2、如果等腰三角形的底角为30°,腰长为6cm,那么这个三角形的面积为( )
A.4.5cm2 B.9cm2 C.18cm2 D.36cm2
3、如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B,取∠ABD=145°,BD=500m,∠D=55°,要使A,C,E成一直线,那么开挖点E离点D的距离是( )
A.500sin55°m B.500cos55°m
C.500tan55°m D.500cot55°m
4、ΔABC中,∠A,∠B都是锐角,且sinA=,tanB=,AB=10,求ΔABC的面积。
5、某型号飞机的翼形状如图所示,根据图中数据计算AC、BD和 CD的长度(精确到0.1米).
(1)边角之间关系:
如果用表示直角三角形的一个锐角,那么
①正弦:
②余弦:
③正切:
(2)三边之间关系:a2 +b2 =c2 (勾股定理)
(3)锐角之间关系:∠A+∠B=90°.
至少知道2个元素(至少有一个是边),就可以求出其余的3个元素
3.40米
5.00米
A
B
C
D
45
30
一、学习目标
使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形
二、自学提纲:
1.在三角形中共有几个元素?
2.直角三角形ABC中,∠C=90°,那么剩下的
a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?
以上三点正是解直角三角形的依据.
思考:在直角三角形的五个元素中,至少知道多少元素才能求出其余的元素
例1:如图,在中,,,,
解这个直角三角形
解:
AB=
练习:在中,,,,解这个直角三角形(可利用用计算器计算)
例题2:如图,中,,,,解这个直角三角形(精确到0.1)
解:
,
,
练习:如图,中,,,,解这个直角三角形
(精确到0.1)
A组:
1、如图中,, c= 8,∠A=60°,请你解这个直角三角形。
解:
BC=
2、如图中,,a=3, ∠A=30°,请你解这个直角三角形。
3、如图中,,a=6,b=2,请你解这个直角三角形
4、如图中,,c=,b=3,求a、A
B组 :
1、已知α为锐角,tanα=,则cosα等于( )
A. B. C. D.
2、如果等腰三角形的底角为30°,腰长为6cm,那么这个三角形的面积为( )
A.4.5cm2 B.9cm2 C.18cm2 D.36cm2
3、如图,沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B,取∠ABD=145°,BD=500m,∠D=55°,要使A,C,E成一直线,那么开挖点E离点D的距离是( )
A.500sin55°m B.500cos55°m
C.500tan55°m D.500cot55°m
4、ΔABC中,∠A,∠B都是锐角,且sinA=,tanB=,AB=10,求ΔABC的面积。
5、某型号飞机的翼形状如图所示,根据图中数据计算AC、BD和 CD的长度(精确到0.1米).
(1)边角之间关系:
如果用表示直角三角形的一个锐角,那么
①正弦:
②余弦:
③正切:
(2)三边之间关系:a2 +b2 =c2 (勾股定理)
(3)锐角之间关系:∠A+∠B=90°.
至少知道2个元素(至少有一个是边),就可以求出其余的3个元素
3.40米
5.00米
A
B
C
D
45
30
