第八单元 立体几何与空间向量(三)(含解析)-《巅峰突破》2026版高中数学高三一轮复习
文档属性
| 名称 | 第八单元 立体几何与空间向量(三)(含解析)-《巅峰突破》2026版高中数学高三一轮复习 |  | |
| 格式 | docx | ||
| 文件大小 | 424.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 11:23:59 | ||
图片预览



文档简介
(
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
(
姓名 班级 考号
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
第八单元 立体几何与空间向量(三)
满分150分,限时120分钟
考点3 空间向量与立体几何
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2025湖南衡阳第四中学期中)已知直线l的方向向量是a=(3,2,1),平面α的一个法向量是n=(1,-1,-1),则l与α的位置关系是( )
A.l⊥α B.l∥α
C.l与α相交但不垂直 D.l∥α或l α
2.(2025四川成都石室成飞中学月考)如图,四面体OABC中,=a,=b,=c,点M在OA上,且=,点N为BC的中点,则等于( )
A.a+b-c B.-a+b+c
C.a+b-c D.a-b-c
3.(2025云南昆明第一中学联考)如图,平行六面体ABCD-A1B1C1D1的所有棱长均为2,四边形ABCD是正方形,∠A1AD=∠A1AB=,点O是B1C与BC1的交点,则直线AO与CD所成角的余弦值为( )
A.1 B. C. D.
4.(2024青海西宁四模)在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=AA1,D为BC的中点,点E在B1C1上,且B1E=B1C1,则直线DE与平面ACC1A1所成角的正弦值为( )
A. B. C. D.
5.(2024陕西渭南期末)在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,∠ABC=,AB=PA=CD=1,BC=2,M为PD的中点,则二面角M-BC-A的余弦值为( )
A. B. C. D.
6.(2024安徽A10联盟联考)《九章算术》是我国古代的数学名著,书中将底面为矩形,且有一条侧棱垂直于底面的四棱锥称为阳马.如图,在阳马P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,AC与BD交于点O,E,F分别为PD,PB的中点,点G满足=λ(0<λ<1),PA=4,AB=2,若OG∥平面CEF,则λ=( )
A. B. C. D.
7.(2025山东聊城颐中外国语学校月考)已知菱形ABCD中,∠DAB=,将△DAC沿对角线AC折起,使以A,B,C,D为顶点的三棱锥的体积最大,此时异面直线AB与CD所成角的余弦值为( )
A.- B. C. D.
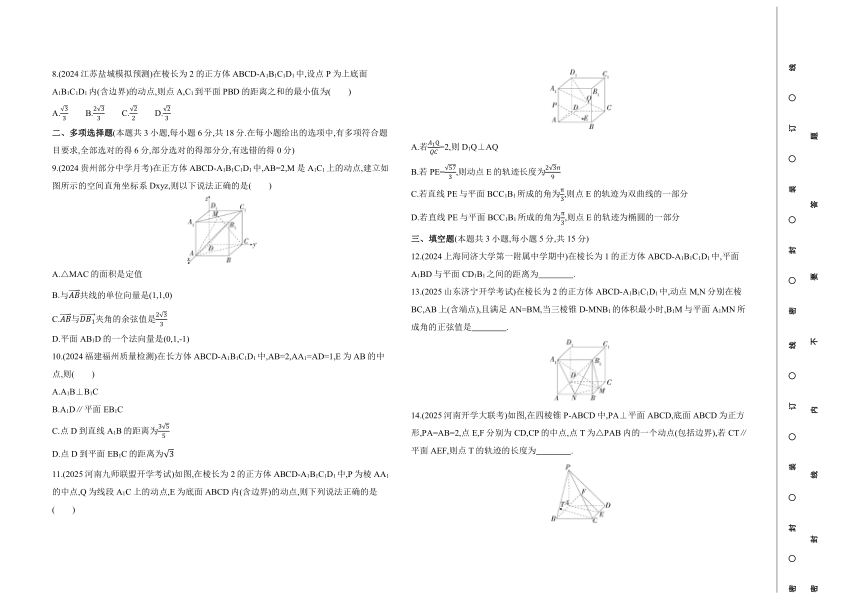
8.(2024江苏盐城模拟预测)在棱长为2的正方体ABCD-A1B1C1D1中,设点P为上底面A1B1C1D1内(含边界)的动点,则点A,C1到平面PBD的距离之和的最小值为( )
A. B. C. D.
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.(2024贵州部分中学月考)在正方体ABCD-A1B1C1D1中,AB=2,M是A1C1上的动点,建立如图所示的空间直角坐标系Dxyz,则以下说法正确的是( )
A.△MAC的面积是定值
B.与共线的单位向量是(1,1,0)
C.与夹角的余弦值是
D.平面AB1D的一个法向量是(0,1,-1)
10.(2024福建福州质量检测)在长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=1,E为AB的中点,则( )
A.A1B⊥B1C
B.A1D∥平面EB1C
C.点D到直线A1B的距离为
D.点D到平面EB1C的距离为
11.(2025河南九师联盟开学考试)如图,在棱长为2的正方体ABCD-A1B1C1D1中,P为棱AA1的中点,Q为线段A1C上的动点,E为底面ABCD内(含边界)的动点,则下列说法正确的是( )
A.若=2,则D1Q⊥AQ
B.若PE=,则动点E的轨迹长度为
C.若直线PE与平面BCC1B1所成的角为,则点E的轨迹为双曲线的一部分
D.若直线PE与平面BCC1B1所成的角为,则点E的轨迹为椭圆的一部分
三、填空题(本题共3小题,每小题5分,共15分)
12.(2024上海同济大学第一附属中学期中)在棱长为1的正方体ABCD-A1B1C1D1中,平面A1BD与平面CD1B1之间的距离为 .
13.(2025山东济宁开学考试)在棱长为2的正方体ABCD-A1B1C1D1中,动点M,N分别在棱BC,AB上(含端点),且满足AN=BM,当三棱锥D-MNB1的体积最小时,B1M与平面A1MN所成角的正弦值是 .
14.(2025河南开学大联考)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,PA=AB=2,点E,F分别为CD,CP的中点,点T为△PAB内的一个动点(包括边界),若CT∥平面AEF,则点T的轨迹的长度为 .
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
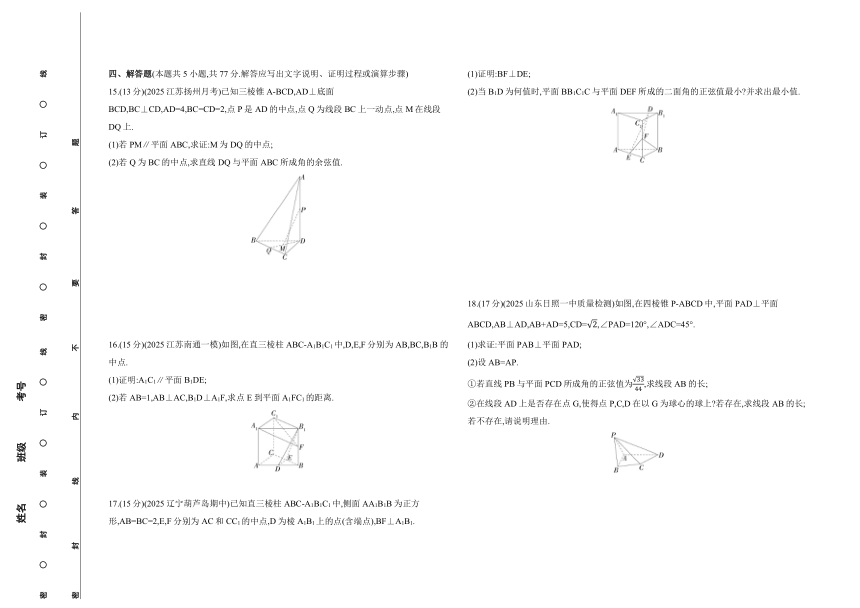
15.(13分)(2025江苏扬州月考)已知三棱锥A-BCD,AD⊥底面BCD,BC⊥CD,AD=4,BC=CD=2,点P是AD的中点,点Q为线段BC上一动点,点M在线段DQ上.
(1)若PM∥平面ABC,求证:M为DQ的中点;
(2)若Q为BC的中点,求直线DQ与平面ABC所成角的余弦值.
16.(15分)(2025江苏南通一模)如图,在直三棱柱ABC-A1B1C1中,D,E,F分别为AB,BC,B1B的中点.
(1)证明:A1C1∥平面B1DE;
(2)若AB=1,AB⊥AC,B1D⊥A1F,求点E到平面A1FC1的距离.
17.(15分)(2025辽宁葫芦岛期中)已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点(含端点),BF⊥A1B1.
(1)证明:BF⊥DE;
(2)当B1D为何值时,平面BB1C1C与平面DEF所成的二面角的正弦值最小 并求出最小值.
18.(17分)(2025山东日照一中质量检测)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB⊥AD,AB+AD=5,CD=,∠PAD=120°,∠ADC=45°.
(1)求证:平面PAB⊥平面PAD;
(2)设AB=AP.
①若直线PB与平面PCD所成角的正弦值为,求线段AB的长;
②在线段AD上是否存在点G,使得点P,C,D在以G为球心的球上 若存在,求线段AB的长;若不存在,请说明理由.
19.(17分)(2024重庆八中检测)如图①,在直角梯形ABCD中,AB∥CD,AD⊥CD,AC⊥BC,将△ACD沿AC折起,使平面ACD⊥平面ABC,连接BD,得到如图②所示的几何体.
(1)证明:平面ACD⊥平面BCD;
(2)若DC=1,二面角C-AD-B的正切值为2,在棱AB上是否存在点M(含端点),使得二面角B-CD-M的余弦值为 若存在,求出的值;若不存在,请说明理由.
答案全解全析
1.D 因为a=(3,2,1),n=(1,-1,-1),所以a·n=3×1+2×(-1)+1×(-1)=0,所以a⊥n,所以l∥α或l α.
2.B 连接AN,则=+=+(+)=+(-)+(-)=-++=-a+b+c.
3.B 取BC的中点F,连接AF,FO,
因为AB∥CD,所以直线AO与CD所成的角即为AO与AB所成的角,
易得=+=++,
所以=++2=22+×22×2+2×2×cos +×2×2×cos =9,即||=3,
又因为·=+·+·=5,
所以cos<,>===,所以直线AO与CD所成角的余弦值为.
4.B 如图,以A为原点,AB,AC,AA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,不妨设AA1=4,则AB=AC=6,
故D(3,3,0),E(4,2,4),故=(1,-1,4),
因为x轴⊥平面ACC1A1,所以可取平面ACC1A1的一个法向量为n=(1,0,0),
则|cos<,n>|===,
即直线DE与平面ACC1A1所成角的正弦值为.
5.A 解法一 取CD的中点E,连接AE,则CE=CD,又AB∥CD,AB=CD,所以AB CE,故四边形ABCE为平行四边形,又∠ABC=,所以平行四边形ABCE为矩形,则AB⊥AE,因为PA⊥平面ABCD,AE,AB 平面ABCD,所以PA⊥AE,PA⊥AB,
以A为原点,AE,AB,AP所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则B(0,1,0),C(2,1,0),P(0,0,1),D(2,-1,0),M,
所以=(2,0,0),=,
设平面BCM的法向量为n=(x,y,z),则即令y=1,则x=0,z=3,
即可取n=(0,1,3),显然可取平面ABC的法向量为m=(0,0,1),易知二面角M-BC-A为锐角,
所以二面角M-BC-A的余弦值为|cos|===.
解法二 延长CB,DA交于点F,连接MF交PA于点G,易知M,G,B,C四点共面,连接GB.
所以只需求平面MGBC和平面ABCD所成的角即可,
因为2AB=CD,AB∥CD,所以AB是△CDF的中位线,故A为DF的中点,连接PF,因为M为DP的中点,所以G是△DPF的重心,即
因为PA⊥平面ABCD,BC 平面ABCD,所以PA⊥BC.又因为BC⊥AB,AB∩AP=A,AB,AP 平面PAB,所以BC⊥平面PAB,又GB 平面PAB,所以GB⊥BC.
又平面MGBC∩平面ABCD=BC,所以∠GBA即为平面MGBC和平面ABCD所成的角.
在Rt△GAB中,GB===,故cos∠GBA==.
6.B 解法一 因为PA⊥平面ABCD,AB,AD 平面ABCD,所以PA⊥AB,PA⊥AD.因为底面ABCD是正方形,所以AB⊥AD,所以AP,AB,AD两两垂直.
以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图.
则O(1,1,0),C(2,2,0),E(0,1,2),F(1,0,2),
所以=(1,-1,0),=(2,1,-2).
设平面CEF的法向量为m=(x,y,z),
则
令x=2,则y=2,z=3,所以m=(2,2,3).
设G(0,0,a),0即-1×2-1×2+3a=0,解得a=,所以AG=,
所以λ==.
解法二 过点C作CM∥DB,交AD的延长线于点M,连接ME并延长交AP于点N,
因为E,F分别为PD,PB的中点,所以EF∥BD,又BD∥CM,所以EF∥CM.
又EM交AP于点N,所以F,C,M,E,N五点共面.
连接CN,则平面CEF∩平面PAC=CN,又OG∥平面CEF,OG 平面PAC,所以OG∥CN,
过点D作DQ∥AP,交MN于点Q.
因为E是PD的中点,所以NP=QD,易知四边形BCMD为平行四边形,故DM=BC,即D为AM的中点,所以AN=2DQ,故AN=2NP,又O是AC的中点,OG∥CN,所以AG=GN,即AG=NG=NP,所以=,所以λ=.
7.C 取AC的中点E,连接DE,BE,因为AD=CD,所以DE⊥AC,同理,BE⊥AC,
又BE∩DE=E,BE,DE 平面BDE,所以AC⊥平面BDE,VD-ABC=VA-BDE+VC-BDE=S△BED(AE+EC)=S△BED·AC,故要使三棱锥D-ABC的体积最大,只需使S△BED最大,而DE,BE均为定值,所以此时∠BED=.
记AB=2a,在菱形ABCD中,∠DAB=,所以∠DAC=∠BAC=,所以BE=DE=a,AE=CE=a,
因为DE⊥BE,DE⊥AC,BE∩AC=E,BE,AC 平面ABC,所以DE⊥平面ABC.
故以E为原点,,,的方向分别为x,y,z轴的正方向建立空间直角坐标系,
则A(0,-a,0),B(a,0,0),C(0,a,0),D(0,0,a),所以=(a,a,0),=(0,-a,a),
所以|cos<,>|===,所以异面直线AB与CD所成角的余弦值为.
8.B 建立空间直角坐标系,如图所示,
则D(0,0,0),A(2,0,0),B(2,2,0),C1(0,2,2),设P(a,b,2),0≤a≤2,0≤b≤2,
所以=(2,0,0),=(0,2,2),=(2,2,0),=(a,b,2),设平面PBD的法向量为m=(x,y,z),
则令x=2,则y=-2,z=b-a.所以m=(2,-2,b-a),设点A,C1到平面PBD的距离分别为d1,d2.
则点A,C1到平面PBD的距离之和为d1+d2=+=+,
设b-a=t,,
故d1+d2=+==2
=2=2,
因为t∈[-2,2],
所以4-t∈[2,6],
所以∈,
易得函数y=1-8x+24x2的图象开口向上,对称轴方程为x=,故该函数在上单调递增,
所以当=时,d1+d2取到最小值,为.
9.AD A选项,∵M在A1C1上且A1C1∥AC,∴M到AC的距离等于A1C1到AC的距离,为定值2,又AC=2,∴S△MAC=×2×2=2,为定值,故A正确;
B选项,向量(1,1,0)的模为,不是单位向量,故B错误;
C选项,易知A(2,0,0),B(2,2,0),D(0,0,0),B1(2,2,2),
则=(0,2,0),=(2,2,2),=(-2,0,0),
cos<,>===,故C错误;
D选项,令n=(0,1,-1),则·n=2×0+2×1+2×(-1)=0,·n=-2×0+0×1+0×(-1)=0,即⊥n,⊥n,又B1D∩AD=D,B1D,AD 平面AB1D,
∴(0,1,-1)为平面AB1D的一个法向量,故D正确.
选项速解
D选项,连接A1B,因为A1B⊥AB1,A1B⊥AD,AB1∩AD=A,AB1,AD 平面AB1D,所以A1B⊥平面AB1D,所以为平面AB1D的一个法向量,易知=(0,2,-2)=2(0,1,-1),故D正确.
10.BC 如图,建立空间直角坐标系Dxyz,易知D(0,0,0),A1(1,0,1),B(1,2,0),B1(1,2,1),C(0,2,0),E(1,1,0).
对于A,=(0,2,-1),=(-1,0,-1),则·=1≠0,故A错误;
对于B,易知A1D∥B1C,由A1D 平面EB1C,B1C 平面EB1C,得A1D∥平面EB1C,故B正确;
对于C,解法一 记直线A1B的单位向量为u,则u==,过D作DQ⊥A1B,交A1B于Q,易得=(-1,0,-1),
所以向量在直线A1B上的投影向量为=·u=,
则D到直线A1B的距离为DQ==,故C正确;
解法二 在△DBA1中,因为A1B=DB=,A1D=,
所以=A1D·=,设点D到直线A1B的距离为h,则=A1B·h,
所以h==,故C正确;
对于D,解法一 设平面EB1C的法向量为m=(x,y,z),易求得=(0,-1,-1),
则令x=1,可得m=(1,1,-1),
又=(0,2,0),所以点D到平面EB1C的距离d==,故D错误.
解法二 设点D到平面EB1C的距离为d,
因为=·d,==S△DEC·BB1=××2×1×1=,所以d===,故D错误.
知识总结 利用空间向量求距离
(1)点A到直线l的距离d=,其中A l,B∈l,a是直线l的一个方向向量.
(2)点A到平面α的距离d=,其中A α,B∈α,n是平面α的一个法向量.
(3)两平行直线之间的距离可转化为点到直线的距离.
(4)平行的线面、面面之间的距离可转化为点到平面的距离.
11.ABC 对于A,连接AC,AD1,
则AC=AD1=2,
作QF⊥AC,交AC于点F,易证QF∥AA1,
由=2,得=,=,
所以QF=,AF=,
所以AQ==2,
同理D1Q=2,所以AQ2+D1Q2=A,故D1Q⊥AQ,故A正确;
对于B,连接AE,易知AP⊥AE,
故PE==,
又PA=AA1=1,所以AE=,
易知2<<2,则点E的轨迹是以A为圆心,为半径的圆在正方形ABCD内(含边界)的部分,设该圆交CD于S点,交CB于R点,则cos∠DAS=cos∠BAR=,
又∠DAS,∠BAR为锐角,所以∠DAS=∠BAR=,所以∠RAS=,故所求的,故B正确;
对于C,D,以A为坐标原点建立如图所示的空间直角坐标系,则P(0,0,1),设E(x,y,0),-2≤x≤0,0≤y≤2,则=(x,y,-1),取平面BCC1B1的一个法向量为n=(0,1,0),
因为直线PE与平面BCC1B1所成的角为,
所以sin =|cos<,n>|=
==,化简得-x2=1,故C正确,D错误.
12.
解析 建立空间直角坐标系,如图所示,
则A1(1,0,1),B(1,1,0),D(0,0,0),C(0,1,0),
所以=(1,0,1),=(1,1,0),=(0,1,0).
易知平面A1BD∥平面CD1B1.
设平面A1BD的法向量为n=(x,y,z),
则
令x=1,得y=-1,z=-1,
所以n=(1,-1,-1).
所以平面A1BD与平面CD1B1之间的距离
13.
解析 设AN=x(0≤x≤2),则S△DMN=2×2-×2x-(2-x)x-×2(2-x)=2-(2-x)x.
由等体积法得==×2×S△DMN=-(2-x)·x=(x-1)2+1,0≤x≤2,
故当x=1时,三棱锥D-MNB1的体积最小,此时M,N分别是所在棱的中点.
解法一 以D为原点,,,的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系,
则N(2,1,0),M(1,2,0),A1(2,0,2),B1(2,2,2).
所以=(1,-1,0),=(-1,2,-2),=(1,0,2).
设平面A1MN的法向量为n=(x,y,z),
则即令x=1,得y=1,z=,
则n=.设B1M与平面A1MN所成的角为θ,
则sin θ=|cos|=
==.
解法二 易知A1N=B1M=,A1M=3,MN=.
在△A1MN中,由余弦定理的推论得cos∠A1MN==,所以sin∠A1MN=,
所以=××3×=.
设点B1到平面A1MN的距离为h.根据=,
得××2×2×1=××h,解得h=.
所以B1M与平面A1MN所成角的正弦值为==.
14.
解析 取AB的中点G,连接CG,
因为四边形ABCD为正方形,E为CD的中点,所以AG∥CE,且AG=CE,所以四边形AGCE为平行四边形,故CG∥AE,
又CG 平面AEF,AE 平面AEF,所以CG∥平面AEF,
记点T的轨迹与PB交于点H,连接GH,由题知CH∥平面AEF,
因为CH∩CG=C,CH,CG 平面CHG,所以平面CHG∥平面AEF,又GH 平面CHG,所以GH∥平面AEF,因为平面CHG∩平面PAB=GH,所以GH即为点T的运动轨迹,
由题知,AB,AD,AP两两垂直,以A为原点,AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系,则A(0,0,0),E(1,2,0),F(1,1,1),C(2,2,0),P(0,0,2),B(2,0,0),
所以=(2,0,-2),=(-2,-2,2),=(1,2,0),=(1,1,1),
设=λ(0≤λ≤1),则=+=+λ=(-2,-2,2)+λ(2,0,-2)=(2λ-2,-2,2-2λ),
设n=(x,y,z)为平面AEF的法向量,
则
令y=1,得n=(-2,1,1),
因为⊥n,所以-2(2λ-2)-2+2-2λ=0,解得λ=,则=,又==(1,2,0),所以=+=(1,2,0)+=,
所以||==.
15.解析 (1)证明:连接AQ,因为PM∥平面ABC,PM 平面ADQ,平面ADQ∩平面ABC=AQ,所以PM∥AQ,(3分)
又因为P是AD的中点,所以M是DQ的中点.(5分)
(2)解法一 因为AD⊥底面BCD,BC⊥CD,所以可以建立如图所示的空间直角坐标系,(6分)
则C(0,0,0),D(2,0,0),B(0,2,0),A(2,0,4),Q(0,1,0),得=(-2,1,0),=(2,0,4),=(0,2,0),(8分)
设平面ABC的法向量为n=(x,y,z),则
令z=1,则y=0,x=-2,可得n=(-2,0,1),(10分)
则cos<,n>===,
设直线DQ与平面ABC所成的角为θ,则sin θ=|cos<,n>|=,(12分)
又θ∈,所以cos θ=,因此直线DQ与平面ABC所成角的余弦值为.(13分)
解法二 过点D作DN⊥AC交AC于N,连接QN,
因为AD⊥底面BCD,BC 底面BCD,所以AD⊥BC,
又BC⊥CD,AD∩CD=D,AD,CD 平面ACD,所以BC⊥平面ACD,(6分)
由DN 平面ACD,可得BC⊥DN,
又AC∩BC=C,AC,BC 平面ABC,
所以DN⊥平面ABC,(8分)
可知∠DQN即为直线DQ与平面ABC所成的角,(9分)
在Rt△ACD中,CD=2,AD=4,则AC=2,
∴DN=,又DQ=,∴QN==,(11分)
则cos∠DQN==,∴直线DQ与平面ABC所成角的余弦值为.(13分)
解法三 设点D到平面ABC的距离为d,直线DQ与平面ABC所成的角为θ,由线面角的定义可知sin θ=.
因为AD⊥平面BCD,BC 平面BCD,所以AD⊥BC.(7分)
又BC⊥CD,CD∩AD=D,CD,AD 平面ACD,
所以BC⊥平面ACD,
又AC 平面ACD,所以BC⊥AC.
故S△ABC=BC·AC=×2×2=2.(9分)
由VD-ABC=VA-BCD得S△ABC×d=××2×2×4,故d==,(11分)
易得DQ==,所以sin θ==,(12分)
易知θ为锐角,故cos θ==,所以直线DQ与平面ABC所成角的余弦值为.(13分)
方法总结 求线面角的三种常见方法
如图,求直线AB和平面α所成的角:
(1)利用定义构造射影BC,转为斜线AB和射影BC所成的角;
(2)利用等体积法求出点A到平面α的距离AC的长,则sin θ=;
(3)利用向量法,sin θ=.
16.解析 (1)证明:在直三棱柱ABC-A1B1C1中,易知A1C1∥AC,(1分)
又D,E分别为AB,BC的中点,所以DE∥AC,(2分)
所以DE∥A1C1,(4分)
又A1C1 平面B1DE,DE 平面B1DE,所以A1C1∥平面B1DE.(6分)
(2)解法一 以A为坐标原点,AB,AC,AA1所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,(7分)
设AA1=a(a>0),则B1(1,0,a),D,A1(0,0,a),F,
则=,=,(9分)
由B1D⊥A1F可得·=0,即-+=0,所以a=1,则=,(11分)
设AC=b(b>0),则C1(0,b,1),故=(0,b,0),
设平面A1FC1的法向量为n=(x,y,z),
则解得
取x=1,则z=2,所以平面A1FC1的一个法向量为n=(1,0,2),(13分)
又E,
所以=,
所以点E到平面A1FC1的距离d===.(15分)
解法二 在矩形AA1B1B中,因为B1D⊥A1F,所以△DBB1∽△FB1A1,
故=,即=,解得BB1=1.(8分)
过点A1作A1G⊥B1C1(图略),因为BB1⊥平面A1B1C1,A1G 平面A1B1C1,所以BB1⊥A1G,又B1C1∩BB1=B1,B1C1,BB1 平面BB1C1C,所以A1G⊥平面BB1C1C,
故=·A1G,设点E到平面A1FC1的距离为d,则=·d,
又=,所以d=,(10分)
设AC=a,则=--S△BEF-=,A1G==,(12分)
因为AB⊥AC,所以A1B1⊥A1C1,
又A1C1⊥BB1,A1B1∩BB1=B1,A1B1,BB1 平面A1ABB1,
所以A1C1⊥平面A1ABB1,
又A1F 平面A1ABB1,所以A1C1⊥A1F,故=A1C1×A1F=a,(13分)
所以d===.(15分)
17.解析 (1)证明:在正方形AA1B1B中,易知BB1⊥AB,
因为A1B1∥AB,BF⊥A1B1,所以BF⊥AB,(1分)
又BB1∩BF=B,BB1,BF 平面BCC1B1,
所以AB⊥平面BCC1B1.(2分)
又BC 平面BCC1B1,所以AB⊥BC,易知BB1⊥BC,所以BA,BC,BB1两两垂直.
以B为坐标原点,BA,BC,BB1所在直线分别为x,y,z轴建立空间直角坐标系,
则B(0,0,0),E(1,1,0),F(0,2,1).(4分)
设D(a,0,2)(0≤a≤2),
易得=(0,2,1),=(1-a,1,-2),
所以·=0×(1-a)+2×1+1×(-2)=0,所以BF⊥DE.(6分)
(2)解法一 设平面DEF的法向量为m=(x,y,z),
由(1)得=(-1,1,1),=(1-a,1,-2),
所以即令z=2-a,则m=(3,1+a,2-a),(8分)
因为AB⊥平面BCC1B1,所以平面BCC1B1的一个法向量为=(2,0,0),(10分)
设平面BCC1B1与平面DEF的二面角的大小为θ,
则|cos θ|===.(12分)
当a=时,2a2-2a+14取最小值,为,此时cos θ取最大值,为=.(14分)
所以(sin θ)min==,此时B1D=.(15分)
解法二 如图,取BC的中点N,连接FB1,FN,EN,B1N,EB,则EN∥AB,EN⊥平面BB1C1C,EN=AB=1,
易知△DEF在平面BB1C1C内的射影为△B1NF,(7分)
记平面BB1C1C与平面DEF所成的二面角的大小为θ,,(8分)
设B1D=t(0≤t≤2),
在Rt△DB1F中,DF==.
在Rt△ECF中,EF==,
过D作B1N的平行线交EN于点Q,又EN∥A1B1,所以四边形DQNB1为平行四边形,
在Rt△DEQ中,DE==.
在△DEF中,由余弦定理的推论得cos∠DFE==,(10分)
则sin∠DFE=,
故S△DEF=DF·EFsin∠DFE=,(12分)
易得+S△CNF+=1++1=,=4-=,
所以cos θ==,则sin θ=,(14分)
当t=,即B1D=时,平面BB1C1C与平面DEF所成的二面角的正弦值最小,为.(15分)
方法拓展 射影法求二面角
已知平面β内一个多边形的面积为S1,它在平面α内的射影图形的面积为S2,平面α和平面β所成的二面角的大小为θ,则cos θ=.此方法经常用于求无棱二面角的大小.
18.解析 (1)证明:因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,AB⊥AD,AB 平面ABCD,所以AB⊥平面PAD,(3分)
又AB 平面PAB,所以平面PAB⊥平面PAD.(4分)
(2)以A为原点,AB,AD所在直线分别为x,y轴,与平面ABCD垂直的直线为z轴建立如图所示的空间直角坐标系Axyz,
设AB=t,0故B(t,0,0),P,D(0,5-t,0),C(1,4-t,0),所以=,=(-1,1,0),(6分)
①设平面PCD的法向量为n=(x,y,z),
则即
可取n=,(7分)
设直线PB与平面PCD所成的角为θ,
则sin θ=|cos|,
又=,
所以=,(9分)
化简得23t2-116t+140=0,解得t=2或t=,即AB=2或AB=.(11分)
②不存在,理由如下:假设在线段AD上存在点G,使得点P,C,D在以G为球心的球上,
=45°,所以∠CGD=90°,所以GD=CDcos 45°=1,(12分)
由AB=t,AD=5-t,得AG=4-t,所以G(0,4-t,0),P,(13分)
由GP=GD,得+=1,
即t2-4t+15=0(*),(15分)
因为Δ=(-4)2-4×15<0,
所以方程(*)无实数解,
所以线段AD上不存在点G,使得点P,C,D在以G为球心的球上.(17分)
19.解析 (1)证明:因为平面ACD⊥平面ABC,平面ACD∩平面ABC=AC,AC⊥BC,BC 平面ABC,所以BC⊥平面ACD.又AD 平面ACD,所以BC⊥AD.(3分)
因为AD⊥CD,CD∩BC=C,CD,BC 平面BCD,
所以AD⊥平面BCD.
又AD 平面ACD,所以平面ACD⊥平面BCD.(5分)
(2)由(1)知AD⊥平面BCD,又BD 平面BCD,所以AD⊥BD.又AD⊥CD,所以∠CDB为二面角C-AD-B的平面角,所以tan∠CDB=2.(6分)
因为BC⊥平面ACD,CD 平面ACD,
所以BC⊥CD,所以∠DCB=90°,
故tan∠CDB==2,
所以BC=2,BD=.(7分)
在题图①中,易知Rt△ACD∽Rt△BAC,所以=.
令AD=x,则=,所以x=2,
所以AD=2,故AC=.
以C为坐标原点,CA,CB所在直线分别为x轴,y轴,与平面ACB垂直的直线为z轴建立如图所示的空间直角坐标系,
过点D作DH⊥AC,垂足为H,则DH=,CH=.(9分)
则C(0,0,0),A(,0,0),B(0,2,0),D,所以=(0,2,0),=,=(-,2,0),=(,0,0),
设=λ=(-λ,2λ,0),0≤λ≤1.
则=+=((1-λ),2λ,0).(11分)
设平面CBD的法向量为n1=(x1,y1,z1),
则
取x1=2,则z1=-1,所以n1=(2,0,-1),(13分)
设平面CMD的法向量为n2=(x2,y2,z2),
则
取x2=2λ,则y2=λ-1,z2=-λ,所以n2=(2λ,λ-1,-λ),(15分)
若二面角B-CD-M的余弦值为,
则|cos|===,
解得λ=3(舍去)或λ=,所以存在点M,使得二面角B-CD-M的余弦值为,此时=.(17分)
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
(
姓名 班级 考号
密 ○ 封 ○ 装 ○ 订 ○ 线 密 ○ 封 ○ 装 ○ 订 ○ 线
密 封 线 内 不 要 答 题
)
第八单元 立体几何与空间向量(三)
满分150分,限时120分钟
考点3 空间向量与立体几何
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2025湖南衡阳第四中学期中)已知直线l的方向向量是a=(3,2,1),平面α的一个法向量是n=(1,-1,-1),则l与α的位置关系是( )
A.l⊥α B.l∥α
C.l与α相交但不垂直 D.l∥α或l α
2.(2025四川成都石室成飞中学月考)如图,四面体OABC中,=a,=b,=c,点M在OA上,且=,点N为BC的中点,则等于( )
A.a+b-c B.-a+b+c
C.a+b-c D.a-b-c
3.(2025云南昆明第一中学联考)如图,平行六面体ABCD-A1B1C1D1的所有棱长均为2,四边形ABCD是正方形,∠A1AD=∠A1AB=,点O是B1C与BC1的交点,则直线AO与CD所成角的余弦值为( )
A.1 B. C. D.
4.(2024青海西宁四模)在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=AA1,D为BC的中点,点E在B1C1上,且B1E=B1C1,则直线DE与平面ACC1A1所成角的正弦值为( )
A. B. C. D.
5.(2024陕西渭南期末)在四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,∠ABC=,AB=PA=CD=1,BC=2,M为PD的中点,则二面角M-BC-A的余弦值为( )
A. B. C. D.
6.(2024安徽A10联盟联考)《九章算术》是我国古代的数学名著,书中将底面为矩形,且有一条侧棱垂直于底面的四棱锥称为阳马.如图,在阳马P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,AC与BD交于点O,E,F分别为PD,PB的中点,点G满足=λ(0<λ<1),PA=4,AB=2,若OG∥平面CEF,则λ=( )
A. B. C. D.
7.(2025山东聊城颐中外国语学校月考)已知菱形ABCD中,∠DAB=,将△DAC沿对角线AC折起,使以A,B,C,D为顶点的三棱锥的体积最大,此时异面直线AB与CD所成角的余弦值为( )
A.- B. C. D.
8.(2024江苏盐城模拟预测)在棱长为2的正方体ABCD-A1B1C1D1中,设点P为上底面A1B1C1D1内(含边界)的动点,则点A,C1到平面PBD的距离之和的最小值为( )
A. B. C. D.
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.(2024贵州部分中学月考)在正方体ABCD-A1B1C1D1中,AB=2,M是A1C1上的动点,建立如图所示的空间直角坐标系Dxyz,则以下说法正确的是( )
A.△MAC的面积是定值
B.与共线的单位向量是(1,1,0)
C.与夹角的余弦值是
D.平面AB1D的一个法向量是(0,1,-1)
10.(2024福建福州质量检测)在长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=1,E为AB的中点,则( )
A.A1B⊥B1C
B.A1D∥平面EB1C
C.点D到直线A1B的距离为
D.点D到平面EB1C的距离为
11.(2025河南九师联盟开学考试)如图,在棱长为2的正方体ABCD-A1B1C1D1中,P为棱AA1的中点,Q为线段A1C上的动点,E为底面ABCD内(含边界)的动点,则下列说法正确的是( )
A.若=2,则D1Q⊥AQ
B.若PE=,则动点E的轨迹长度为
C.若直线PE与平面BCC1B1所成的角为,则点E的轨迹为双曲线的一部分
D.若直线PE与平面BCC1B1所成的角为,则点E的轨迹为椭圆的一部分
三、填空题(本题共3小题,每小题5分,共15分)
12.(2024上海同济大学第一附属中学期中)在棱长为1的正方体ABCD-A1B1C1D1中,平面A1BD与平面CD1B1之间的距离为 .
13.(2025山东济宁开学考试)在棱长为2的正方体ABCD-A1B1C1D1中,动点M,N分别在棱BC,AB上(含端点),且满足AN=BM,当三棱锥D-MNB1的体积最小时,B1M与平面A1MN所成角的正弦值是 .
14.(2025河南开学大联考)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,PA=AB=2,点E,F分别为CD,CP的中点,点T为△PAB内的一个动点(包括边界),若CT∥平面AEF,则点T的轨迹的长度为 .
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)(2025江苏扬州月考)已知三棱锥A-BCD,AD⊥底面BCD,BC⊥CD,AD=4,BC=CD=2,点P是AD的中点,点Q为线段BC上一动点,点M在线段DQ上.
(1)若PM∥平面ABC,求证:M为DQ的中点;
(2)若Q为BC的中点,求直线DQ与平面ABC所成角的余弦值.
16.(15分)(2025江苏南通一模)如图,在直三棱柱ABC-A1B1C1中,D,E,F分别为AB,BC,B1B的中点.
(1)证明:A1C1∥平面B1DE;
(2)若AB=1,AB⊥AC,B1D⊥A1F,求点E到平面A1FC1的距离.
17.(15分)(2025辽宁葫芦岛期中)已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点(含端点),BF⊥A1B1.
(1)证明:BF⊥DE;
(2)当B1D为何值时,平面BB1C1C与平面DEF所成的二面角的正弦值最小 并求出最小值.
18.(17分)(2025山东日照一中质量检测)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB⊥AD,AB+AD=5,CD=,∠PAD=120°,∠ADC=45°.
(1)求证:平面PAB⊥平面PAD;
(2)设AB=AP.
①若直线PB与平面PCD所成角的正弦值为,求线段AB的长;
②在线段AD上是否存在点G,使得点P,C,D在以G为球心的球上 若存在,求线段AB的长;若不存在,请说明理由.
19.(17分)(2024重庆八中检测)如图①,在直角梯形ABCD中,AB∥CD,AD⊥CD,AC⊥BC,将△ACD沿AC折起,使平面ACD⊥平面ABC,连接BD,得到如图②所示的几何体.
(1)证明:平面ACD⊥平面BCD;
(2)若DC=1,二面角C-AD-B的正切值为2,在棱AB上是否存在点M(含端点),使得二面角B-CD-M的余弦值为 若存在,求出的值;若不存在,请说明理由.
答案全解全析
1.D 因为a=(3,2,1),n=(1,-1,-1),所以a·n=3×1+2×(-1)+1×(-1)=0,所以a⊥n,所以l∥α或l α.
2.B 连接AN,则=+=+(+)=+(-)+(-)=-++=-a+b+c.
3.B 取BC的中点F,连接AF,FO,
因为AB∥CD,所以直线AO与CD所成的角即为AO与AB所成的角,
易得=+=++,
所以=++2=22+×22×2+2×2×cos +×2×2×cos =9,即||=3,
又因为·=+·+·=5,
所以cos<,>===,所以直线AO与CD所成角的余弦值为.
4.B 如图,以A为原点,AB,AC,AA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,不妨设AA1=4,则AB=AC=6,
故D(3,3,0),E(4,2,4),故=(1,-1,4),
因为x轴⊥平面ACC1A1,所以可取平面ACC1A1的一个法向量为n=(1,0,0),
则|cos<,n>|===,
即直线DE与平面ACC1A1所成角的正弦值为.
5.A 解法一 取CD的中点E,连接AE,则CE=CD,又AB∥CD,AB=CD,所以AB CE,故四边形ABCE为平行四边形,又∠ABC=,所以平行四边形ABCE为矩形,则AB⊥AE,因为PA⊥平面ABCD,AE,AB 平面ABCD,所以PA⊥AE,PA⊥AB,
以A为原点,AE,AB,AP所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则B(0,1,0),C(2,1,0),P(0,0,1),D(2,-1,0),M,
所以=(2,0,0),=,
设平面BCM的法向量为n=(x,y,z),则即令y=1,则x=0,z=3,
即可取n=(0,1,3),显然可取平面ABC的法向量为m=(0,0,1),易知二面角M-BC-A为锐角,
所以二面角M-BC-A的余弦值为|cos
解法二 延长CB,DA交于点F,连接MF交PA于点G,易知M,G,B,C四点共面,连接GB.
所以只需求平面MGBC和平面ABCD所成的角即可,
因为2AB=CD,AB∥CD,所以AB是△CDF的中位线,故A为DF的中点,连接PF,因为M为DP的中点,所以G是△DPF的重心,即
因为PA⊥平面ABCD,BC 平面ABCD,所以PA⊥BC.又因为BC⊥AB,AB∩AP=A,AB,AP 平面PAB,所以BC⊥平面PAB,又GB 平面PAB,所以GB⊥BC.
又平面MGBC∩平面ABCD=BC,所以∠GBA即为平面MGBC和平面ABCD所成的角.
在Rt△GAB中,GB===,故cos∠GBA==.
6.B 解法一 因为PA⊥平面ABCD,AB,AD 平面ABCD,所以PA⊥AB,PA⊥AD.因为底面ABCD是正方形,所以AB⊥AD,所以AP,AB,AD两两垂直.
以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图.
则O(1,1,0),C(2,2,0),E(0,1,2),F(1,0,2),
所以=(1,-1,0),=(2,1,-2).
设平面CEF的法向量为m=(x,y,z),
则
令x=2,则y=2,z=3,所以m=(2,2,3).
设G(0,0,a),0
所以λ==.
解法二 过点C作CM∥DB,交AD的延长线于点M,连接ME并延长交AP于点N,
因为E,F分别为PD,PB的中点,所以EF∥BD,又BD∥CM,所以EF∥CM.
又EM交AP于点N,所以F,C,M,E,N五点共面.
连接CN,则平面CEF∩平面PAC=CN,又OG∥平面CEF,OG 平面PAC,所以OG∥CN,
过点D作DQ∥AP,交MN于点Q.
因为E是PD的中点,所以NP=QD,易知四边形BCMD为平行四边形,故DM=BC,即D为AM的中点,所以AN=2DQ,故AN=2NP,又O是AC的中点,OG∥CN,所以AG=GN,即AG=NG=NP,所以=,所以λ=.
7.C 取AC的中点E,连接DE,BE,因为AD=CD,所以DE⊥AC,同理,BE⊥AC,
又BE∩DE=E,BE,DE 平面BDE,所以AC⊥平面BDE,VD-ABC=VA-BDE+VC-BDE=S△BED(AE+EC)=S△BED·AC,故要使三棱锥D-ABC的体积最大,只需使S△BED最大,而DE,BE均为定值,所以此时∠BED=.
记AB=2a,在菱形ABCD中,∠DAB=,所以∠DAC=∠BAC=,所以BE=DE=a,AE=CE=a,
因为DE⊥BE,DE⊥AC,BE∩AC=E,BE,AC 平面ABC,所以DE⊥平面ABC.
故以E为原点,,,的方向分别为x,y,z轴的正方向建立空间直角坐标系,
则A(0,-a,0),B(a,0,0),C(0,a,0),D(0,0,a),所以=(a,a,0),=(0,-a,a),
所以|cos<,>|===,所以异面直线AB与CD所成角的余弦值为.
8.B 建立空间直角坐标系,如图所示,
则D(0,0,0),A(2,0,0),B(2,2,0),C1(0,2,2),设P(a,b,2),0≤a≤2,0≤b≤2,
所以=(2,0,0),=(0,2,2),=(2,2,0),=(a,b,2),设平面PBD的法向量为m=(x,y,z),
则令x=2,则y=-2,z=b-a.所以m=(2,-2,b-a),设点A,C1到平面PBD的距离分别为d1,d2.
则点A,C1到平面PBD的距离之和为d1+d2=+=+,
设b-a=t,,
故d1+d2=+==2
=2=2,
因为t∈[-2,2],
所以4-t∈[2,6],
所以∈,
易得函数y=1-8x+24x2的图象开口向上,对称轴方程为x=,故该函数在上单调递增,
所以当=时,d1+d2取到最小值,为.
9.AD A选项,∵M在A1C1上且A1C1∥AC,∴M到AC的距离等于A1C1到AC的距离,为定值2,又AC=2,∴S△MAC=×2×2=2,为定值,故A正确;
B选项,向量(1,1,0)的模为,不是单位向量,故B错误;
C选项,易知A(2,0,0),B(2,2,0),D(0,0,0),B1(2,2,2),
则=(0,2,0),=(2,2,2),=(-2,0,0),
cos<,>===,故C错误;
D选项,令n=(0,1,-1),则·n=2×0+2×1+2×(-1)=0,·n=-2×0+0×1+0×(-1)=0,即⊥n,⊥n,又B1D∩AD=D,B1D,AD 平面AB1D,
∴(0,1,-1)为平面AB1D的一个法向量,故D正确.
选项速解
D选项,连接A1B,因为A1B⊥AB1,A1B⊥AD,AB1∩AD=A,AB1,AD 平面AB1D,所以A1B⊥平面AB1D,所以为平面AB1D的一个法向量,易知=(0,2,-2)=2(0,1,-1),故D正确.
10.BC 如图,建立空间直角坐标系Dxyz,易知D(0,0,0),A1(1,0,1),B(1,2,0),B1(1,2,1),C(0,2,0),E(1,1,0).
对于A,=(0,2,-1),=(-1,0,-1),则·=1≠0,故A错误;
对于B,易知A1D∥B1C,由A1D 平面EB1C,B1C 平面EB1C,得A1D∥平面EB1C,故B正确;
对于C,解法一 记直线A1B的单位向量为u,则u==,过D作DQ⊥A1B,交A1B于Q,易得=(-1,0,-1),
所以向量在直线A1B上的投影向量为=·u=,
则D到直线A1B的距离为DQ==,故C正确;
解法二 在△DBA1中,因为A1B=DB=,A1D=,
所以=A1D·=,设点D到直线A1B的距离为h,则=A1B·h,
所以h==,故C正确;
对于D,解法一 设平面EB1C的法向量为m=(x,y,z),易求得=(0,-1,-1),
则令x=1,可得m=(1,1,-1),
又=(0,2,0),所以点D到平面EB1C的距离d==,故D错误.
解法二 设点D到平面EB1C的距离为d,
因为=·d,==S△DEC·BB1=××2×1×1=,所以d===,故D错误.
知识总结 利用空间向量求距离
(1)点A到直线l的距离d=,其中A l,B∈l,a是直线l的一个方向向量.
(2)点A到平面α的距离d=,其中A α,B∈α,n是平面α的一个法向量.
(3)两平行直线之间的距离可转化为点到直线的距离.
(4)平行的线面、面面之间的距离可转化为点到平面的距离.
11.ABC 对于A,连接AC,AD1,
则AC=AD1=2,
作QF⊥AC,交AC于点F,易证QF∥AA1,
由=2,得=,=,
所以QF=,AF=,
所以AQ==2,
同理D1Q=2,所以AQ2+D1Q2=A,故D1Q⊥AQ,故A正确;
对于B,连接AE,易知AP⊥AE,
故PE==,
又PA=AA1=1,所以AE=,
易知2<<2,则点E的轨迹是以A为圆心,为半径的圆在正方形ABCD内(含边界)的部分,设该圆交CD于S点,交CB于R点,则cos∠DAS=cos∠BAR=,
又∠DAS,∠BAR为锐角,所以∠DAS=∠BAR=,所以∠RAS=,故所求的,故B正确;
对于C,D,以A为坐标原点建立如图所示的空间直角坐标系,则P(0,0,1),设E(x,y,0),-2≤x≤0,0≤y≤2,则=(x,y,-1),取平面BCC1B1的一个法向量为n=(0,1,0),
因为直线PE与平面BCC1B1所成的角为,
所以sin =|cos<,n>|=
==,化简得-x2=1,故C正确,D错误.
12.
解析 建立空间直角坐标系,如图所示,
则A1(1,0,1),B(1,1,0),D(0,0,0),C(0,1,0),
所以=(1,0,1),=(1,1,0),=(0,1,0).
易知平面A1BD∥平面CD1B1.
设平面A1BD的法向量为n=(x,y,z),
则
令x=1,得y=-1,z=-1,
所以n=(1,-1,-1).
所以平面A1BD与平面CD1B1之间的距离
13.
解析 设AN=x(0≤x≤2),则S△DMN=2×2-×2x-(2-x)x-×2(2-x)=2-(2-x)x.
由等体积法得==×2×S△DMN=-(2-x)·x=(x-1)2+1,0≤x≤2,
故当x=1时,三棱锥D-MNB1的体积最小,此时M,N分别是所在棱的中点.
解法一 以D为原点,,,的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系,
则N(2,1,0),M(1,2,0),A1(2,0,2),B1(2,2,2).
所以=(1,-1,0),=(-1,2,-2),=(1,0,2).
设平面A1MN的法向量为n=(x,y,z),
则即令x=1,得y=1,z=,
则n=.设B1M与平面A1MN所成的角为θ,
则sin θ=|cos
==.
解法二 易知A1N=B1M=,A1M=3,MN=.
在△A1MN中,由余弦定理的推论得cos∠A1MN==,所以sin∠A1MN=,
所以=××3×=.
设点B1到平面A1MN的距离为h.根据=,
得××2×2×1=××h,解得h=.
所以B1M与平面A1MN所成角的正弦值为==.
14.
解析 取AB的中点G,连接CG,
因为四边形ABCD为正方形,E为CD的中点,所以AG∥CE,且AG=CE,所以四边形AGCE为平行四边形,故CG∥AE,
又CG 平面AEF,AE 平面AEF,所以CG∥平面AEF,
记点T的轨迹与PB交于点H,连接GH,由题知CH∥平面AEF,
因为CH∩CG=C,CH,CG 平面CHG,所以平面CHG∥平面AEF,又GH 平面CHG,所以GH∥平面AEF,因为平面CHG∩平面PAB=GH,所以GH即为点T的运动轨迹,
由题知,AB,AD,AP两两垂直,以A为原点,AB,AD,AP所在直线分别为x,y,z轴建立空间直角坐标系,则A(0,0,0),E(1,2,0),F(1,1,1),C(2,2,0),P(0,0,2),B(2,0,0),
所以=(2,0,-2),=(-2,-2,2),=(1,2,0),=(1,1,1),
设=λ(0≤λ≤1),则=+=+λ=(-2,-2,2)+λ(2,0,-2)=(2λ-2,-2,2-2λ),
设n=(x,y,z)为平面AEF的法向量,
则
令y=1,得n=(-2,1,1),
因为⊥n,所以-2(2λ-2)-2+2-2λ=0,解得λ=,则=,又==(1,2,0),所以=+=(1,2,0)+=,
所以||==.
15.解析 (1)证明:连接AQ,因为PM∥平面ABC,PM 平面ADQ,平面ADQ∩平面ABC=AQ,所以PM∥AQ,(3分)
又因为P是AD的中点,所以M是DQ的中点.(5分)
(2)解法一 因为AD⊥底面BCD,BC⊥CD,所以可以建立如图所示的空间直角坐标系,(6分)
则C(0,0,0),D(2,0,0),B(0,2,0),A(2,0,4),Q(0,1,0),得=(-2,1,0),=(2,0,4),=(0,2,0),(8分)
设平面ABC的法向量为n=(x,y,z),则
令z=1,则y=0,x=-2,可得n=(-2,0,1),(10分)
则cos<,n>===,
设直线DQ与平面ABC所成的角为θ,则sin θ=|cos<,n>|=,(12分)
又θ∈,所以cos θ=,因此直线DQ与平面ABC所成角的余弦值为.(13分)
解法二 过点D作DN⊥AC交AC于N,连接QN,
因为AD⊥底面BCD,BC 底面BCD,所以AD⊥BC,
又BC⊥CD,AD∩CD=D,AD,CD 平面ACD,所以BC⊥平面ACD,(6分)
由DN 平面ACD,可得BC⊥DN,
又AC∩BC=C,AC,BC 平面ABC,
所以DN⊥平面ABC,(8分)
可知∠DQN即为直线DQ与平面ABC所成的角,(9分)
在Rt△ACD中,CD=2,AD=4,则AC=2,
∴DN=,又DQ=,∴QN==,(11分)
则cos∠DQN==,∴直线DQ与平面ABC所成角的余弦值为.(13分)
解法三 设点D到平面ABC的距离为d,直线DQ与平面ABC所成的角为θ,由线面角的定义可知sin θ=.
因为AD⊥平面BCD,BC 平面BCD,所以AD⊥BC.(7分)
又BC⊥CD,CD∩AD=D,CD,AD 平面ACD,
所以BC⊥平面ACD,
又AC 平面ACD,所以BC⊥AC.
故S△ABC=BC·AC=×2×2=2.(9分)
由VD-ABC=VA-BCD得S△ABC×d=××2×2×4,故d==,(11分)
易得DQ==,所以sin θ==,(12分)
易知θ为锐角,故cos θ==,所以直线DQ与平面ABC所成角的余弦值为.(13分)
方法总结 求线面角的三种常见方法
如图,求直线AB和平面α所成的角:
(1)利用定义构造射影BC,转为斜线AB和射影BC所成的角;
(2)利用等体积法求出点A到平面α的距离AC的长,则sin θ=;
(3)利用向量法,sin θ=.
16.解析 (1)证明:在直三棱柱ABC-A1B1C1中,易知A1C1∥AC,(1分)
又D,E分别为AB,BC的中点,所以DE∥AC,(2分)
所以DE∥A1C1,(4分)
又A1C1 平面B1DE,DE 平面B1DE,所以A1C1∥平面B1DE.(6分)
(2)解法一 以A为坐标原点,AB,AC,AA1所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,(7分)
设AA1=a(a>0),则B1(1,0,a),D,A1(0,0,a),F,
则=,=,(9分)
由B1D⊥A1F可得·=0,即-+=0,所以a=1,则=,(11分)
设AC=b(b>0),则C1(0,b,1),故=(0,b,0),
设平面A1FC1的法向量为n=(x,y,z),
则解得
取x=1,则z=2,所以平面A1FC1的一个法向量为n=(1,0,2),(13分)
又E,
所以=,
所以点E到平面A1FC1的距离d===.(15分)
解法二 在矩形AA1B1B中,因为B1D⊥A1F,所以△DBB1∽△FB1A1,
故=,即=,解得BB1=1.(8分)
过点A1作A1G⊥B1C1(图略),因为BB1⊥平面A1B1C1,A1G 平面A1B1C1,所以BB1⊥A1G,又B1C1∩BB1=B1,B1C1,BB1 平面BB1C1C,所以A1G⊥平面BB1C1C,
故=·A1G,设点E到平面A1FC1的距离为d,则=·d,
又=,所以d=,(10分)
设AC=a,则=--S△BEF-=,A1G==,(12分)
因为AB⊥AC,所以A1B1⊥A1C1,
又A1C1⊥BB1,A1B1∩BB1=B1,A1B1,BB1 平面A1ABB1,
所以A1C1⊥平面A1ABB1,
又A1F 平面A1ABB1,所以A1C1⊥A1F,故=A1C1×A1F=a,(13分)
所以d===.(15分)
17.解析 (1)证明:在正方形AA1B1B中,易知BB1⊥AB,
因为A1B1∥AB,BF⊥A1B1,所以BF⊥AB,(1分)
又BB1∩BF=B,BB1,BF 平面BCC1B1,
所以AB⊥平面BCC1B1.(2分)
又BC 平面BCC1B1,所以AB⊥BC,易知BB1⊥BC,所以BA,BC,BB1两两垂直.
以B为坐标原点,BA,BC,BB1所在直线分别为x,y,z轴建立空间直角坐标系,
则B(0,0,0),E(1,1,0),F(0,2,1).(4分)
设D(a,0,2)(0≤a≤2),
易得=(0,2,1),=(1-a,1,-2),
所以·=0×(1-a)+2×1+1×(-2)=0,所以BF⊥DE.(6分)
(2)解法一 设平面DEF的法向量为m=(x,y,z),
由(1)得=(-1,1,1),=(1-a,1,-2),
所以即令z=2-a,则m=(3,1+a,2-a),(8分)
因为AB⊥平面BCC1B1,所以平面BCC1B1的一个法向量为=(2,0,0),(10分)
设平面BCC1B1与平面DEF的二面角的大小为θ,
则|cos θ|===.(12分)
当a=时,2a2-2a+14取最小值,为,此时cos θ取最大值,为=.(14分)
所以(sin θ)min==,此时B1D=.(15分)
解法二 如图,取BC的中点N,连接FB1,FN,EN,B1N,EB,则EN∥AB,EN⊥平面BB1C1C,EN=AB=1,
易知△DEF在平面BB1C1C内的射影为△B1NF,(7分)
记平面BB1C1C与平面DEF所成的二面角的大小为θ,,(8分)
设B1D=t(0≤t≤2),
在Rt△DB1F中,DF==.
在Rt△ECF中,EF==,
过D作B1N的平行线交EN于点Q,又EN∥A1B1,所以四边形DQNB1为平行四边形,
在Rt△DEQ中,DE==.
在△DEF中,由余弦定理的推论得cos∠DFE==,(10分)
则sin∠DFE=,
故S△DEF=DF·EFsin∠DFE=,(12分)
易得+S△CNF+=1++1=,=4-=,
所以cos θ==,则sin θ=,(14分)
当t=,即B1D=时,平面BB1C1C与平面DEF所成的二面角的正弦值最小,为.(15分)
方法拓展 射影法求二面角
已知平面β内一个多边形的面积为S1,它在平面α内的射影图形的面积为S2,平面α和平面β所成的二面角的大小为θ,则cos θ=.此方法经常用于求无棱二面角的大小.
18.解析 (1)证明:因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,AB⊥AD,AB 平面ABCD,所以AB⊥平面PAD,(3分)
又AB 平面PAB,所以平面PAB⊥平面PAD.(4分)
(2)以A为原点,AB,AD所在直线分别为x,y轴,与平面ABCD垂直的直线为z轴建立如图所示的空间直角坐标系Axyz,
设AB=t,0
①设平面PCD的法向量为n=(x,y,z),
则即
可取n=,(7分)
设直线PB与平面PCD所成的角为θ,
则sin θ=|cos
又=,
所以=,(9分)
化简得23t2-116t+140=0,解得t=2或t=,即AB=2或AB=.(11分)
②不存在,理由如下:假设在线段AD上存在点G,使得点P,C,D在以G为球心的球上,
=45°,所以∠CGD=90°,所以GD=CDcos 45°=1,(12分)
由AB=t,AD=5-t,得AG=4-t,所以G(0,4-t,0),P,(13分)
由GP=GD,得+=1,
即t2-4t+15=0(*),(15分)
因为Δ=(-4)2-4×15<0,
所以方程(*)无实数解,
所以线段AD上不存在点G,使得点P,C,D在以G为球心的球上.(17分)
19.解析 (1)证明:因为平面ACD⊥平面ABC,平面ACD∩平面ABC=AC,AC⊥BC,BC 平面ABC,所以BC⊥平面ACD.又AD 平面ACD,所以BC⊥AD.(3分)
因为AD⊥CD,CD∩BC=C,CD,BC 平面BCD,
所以AD⊥平面BCD.
又AD 平面ACD,所以平面ACD⊥平面BCD.(5分)
(2)由(1)知AD⊥平面BCD,又BD 平面BCD,所以AD⊥BD.又AD⊥CD,所以∠CDB为二面角C-AD-B的平面角,所以tan∠CDB=2.(6分)
因为BC⊥平面ACD,CD 平面ACD,
所以BC⊥CD,所以∠DCB=90°,
故tan∠CDB==2,
所以BC=2,BD=.(7分)
在题图①中,易知Rt△ACD∽Rt△BAC,所以=.
令AD=x,则=,所以x=2,
所以AD=2,故AC=.
以C为坐标原点,CA,CB所在直线分别为x轴,y轴,与平面ACB垂直的直线为z轴建立如图所示的空间直角坐标系,
过点D作DH⊥AC,垂足为H,则DH=,CH=.(9分)
则C(0,0,0),A(,0,0),B(0,2,0),D,所以=(0,2,0),=,=(-,2,0),=(,0,0),
设=λ=(-λ,2λ,0),0≤λ≤1.
则=+=((1-λ),2λ,0).(11分)
设平面CBD的法向量为n1=(x1,y1,z1),
则
取x1=2,则z1=-1,所以n1=(2,0,-1),(13分)
设平面CMD的法向量为n2=(x2,y2,z2),
则
取x2=2λ,则y2=λ-1,z2=-λ,所以n2=(2λ,λ-1,-λ),(15分)
若二面角B-CD-M的余弦值为,
则|cos
解得λ=3(舍去)或λ=,所以存在点M,使得二面角B-CD-M的余弦值为,此时=.(17分)
同课章节目录
