北师大版高中数学选择性必修第一册 6.1.3 全概率公式 课件(共30张PPT)
文档属性
| 名称 | 北师大版高中数学选择性必修第一册 6.1.3 全概率公式 课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
6.1.3全概率公式
温故知新
1. 条件概率:
在事件A发生的条件下,事件B发生的概率称为条件概率,即
由条件概率公式可得
2. 概率的乘法公式:
3. 条件概率的性质:
条设P(A)>0, 则
(1)P(Ω|A)=1;
(2)如果B和C是两个互斥事件, 则P(B∪C|A)=P(B|A)+P(C|A);
设A和B是两个独立事件, 则P(B|A)=P(B)或P(A|B)=P(A).
求复杂事件的概率常分成两个(或多个)互斥的较简单的事件之和的概率。
注意顺序!先发生的事件,写在前面
新课导入
在上节计算按对银行储蓄卡密码的概率时,我们首先把一个复杂事件表示为一些简单事件运算的结果,然后利用概率的加法和乘法公式求其概率。
本节,我们再根据一个求复杂事件概率问题出发学习。
解
引例
因为 B=AB +
,且AB与
互不相容,所以
= 0.6
一个盒子中有6只白球、4只黑球,从中不放回地每次任取1只,连取2次,求第二次取到白球的概率
例
A=“第一次取到白球” B=“第二次取到白球”
实例分析
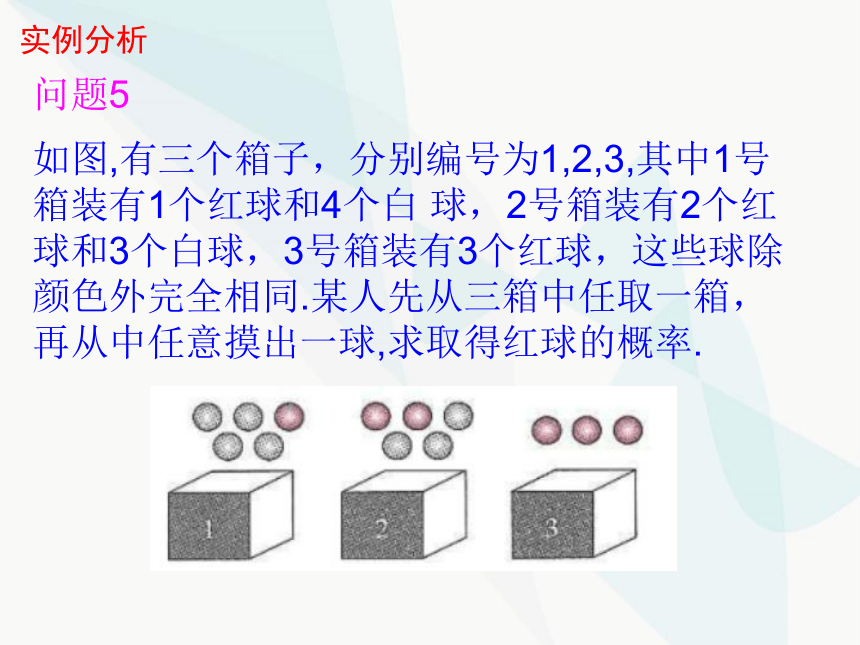
如图,有三个箱子,分别编号为1,2,3,其中1号箱装有1个红球和4个白 球,2号箱装有2个红球和3个白球,3号箱装有3个红球,这些球除颜色外完全相同.某人先从三箱中任取一箱,再从中任意摸出一球,求取得红球的概率.
问题5
按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂事件的概率.
【规律方法】
某电子设备制造厂所用的元件是由三家元件制造厂提供的,根据以往的记录 有如表的数据:
设这三家元件制造厂的元件在仓库中是均匀混合的,且无区别的标志.在仓库中随机地取一只元件,求它是次品的概率.
元件制造厂 次品率 提供元件的份额
1 0.02 0.15
2 0.01 0.80
3 0.03 0.05
问题6
分析 设事件Bi表示“所取到的产品是由第i家元件制造厂提供的”(i=1,2,3),事件A 表示“取到的是一件次品”.其中B1,B2,B3两两互斥,A发生总是伴随着 B1,B2,B3 之一同时发生.即A=B1A∪B2A ∪ B3A,且B1A,B2A,B3A两两互斥.运用互斥事件概率的加法公式和乘法公式,得 P(A) =P(B1A) +P(B2A) +P(B3A)
=F(B1)P(A|B1)+P(B2)P(A|B2)-P(B3)F(A|B3)
=0.15×0.02+ 0.80×0.01+0.05×0.03
=0.0125.
因此,在仓库中随机地取一只元件,它是次品的概率为0.0125.
从上述两个问题可以看出,某一事件A的发生有各种可能的原因,如问题1中摸得的红球有三种来源:可能取自1号箱,也可能取自2号箱或3号箱;问题2中取到的次品可能产自第1家元件制造厂,也可能产自第2家元件制造厂或第3家元件制造厂.若A是由原因 Bi(Bi=1,2,…n)所引起,则A发生的概率是
P(ABi)=P(Bi)P(A|Bi)
由于每一个原因都 可能导致A发生,且各原因涵盖所有可能的情形并彼此互斥,故事件A发生的概率是各原 因引起A发生概率的总和,即
设Ω是试验E的样本空间,B1,B2,…,Bn为样本空间的一组事件,若
(1)BiBj= ,其中i≠j(i,j=1,2,…,n),
(2)B1∪B2∪…∪Bn=Ω
则称B1,B2,…Bn为样本空间的一个划分.
条件(1)表示每次试验B1,B2,…Bn中只能发生一个;
条件(2)表示每次试验B1,B2,…Bn必有发生一个.
全概率公式
例1 釆购员要购买某种电器元件一包(10个).他的采购方法是:从一包中随机抽查 3个,如这3个元件都是好的,他才买下这一包.假定含有4个次品的包数占30%,而其余包中各含1个次品,求采购员随机挑选一包拒绝购买的概率.
从而由全概率公式,可知
因此,釆购员随机挑选一包
拒绝购买的概率为 .
变式: 某学校有 A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐. 如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8. 计算王同学第2天去A餐厅用餐的概率.
设A1=“第1天去A餐厅”, B1=“第1天取B餐厅”, A2=“第2天去A餐厅”, 则
解:
例2 甲、乙、丙三人同时对飞机进行射击,三人击中的概率分别为0.4,0.5,0.7.飞机被一人击中且击落的概率为0.2,被两人击中且击落的概率为0.6,若三人都击中,飞机必定被击落,求飞机被击落的概率.
解 设事件A表示“飞机被击落”,事件Bi表示“飞机被i人击中”(i=0,1,2,3),则B0,构成样本空间的一个划分,且依题意,P(A|B0)=0,P(A|B1)=0.2,P(A|B2)=0.6, P(A|B3) = 1.
再设事件Hi表示“飞机被第i人击中”i=1,2,3).
则
同理
由全概率公式,可知
因此,飞机被击落的概率为0.458.
运用全概率公式的一般步骤如下:
(1)求出样本空间Ω的一个划分B1,B2,…,Bn;
(2)求P(Bi)(i=l,2,…,n);
(3)求P(A|Bi) (i=l,2,…,n);
(4)求目标事件的概率P(A).
可以形象地把全概率公式看成“由原因推结果”,每个原因对结果的发生有一定的“作用”,即结果发生的可能性与各种原因的“作用”大小有关.全概率公式表达了它们之间的关系.
总结
在实际中,还有一类问题是“已知结果求原因".这类问题更为常见,它所求的是条件概率,是已知某结果发生条件下,探求各原因发生的可能性大小.
例3 如图,有三个箱子,分别编号为1,2,3,其中 1号箱装有1个红球和4个白球,2号箱装有2个红球和3个白球,3号箱装有3个红球,这些球除颜色外完全相同.某人先从三箱中任取一箱,再从中任意摸出一球,发现是红球,求该球是取自1号箱的概率以及该球取自几号箱的可能性最大.
解设事件Bi表示“球取自i号箱”(i=1,2,3),
事件A表示“取得红球”.
由全概率公式,可得
P(A) = P(B1)F(A|B1)+F(B2)F(A|B2)+F(B3)P(A|B3)
再由条件概率知,
因此,该球是取自1号箱的概率为 ,该球取自3号箱的可能性最大.
解
= 0.6
变式1:一个盒子中有6只白球、4只黑球,从中不放回地每次任取1只,连取2次,求第二次取到白球的概率
A={第一次取到白球} B={第二次取到白球}
变式2: 商店销售一批收音机10台,其中3台次品,但是已经售出2台,问从剩下的收音机中,任取一台为正品的概率是多少
解: 设A1表示售出的两台均为正品,A2表示售出的两台为一件正品和一件次品,A3表示售出的两台均为次品,则A1,A2,A3是完备事件组.
设B表示从剩下的收音机中任取一台为正品,
变式3: 设播种用麦种中混有一等,二等,三等,四等四个等级的种子,分别各占95.5%,2%,1.5%,1%,用一等,二等,三等,四等种子长出的穗含50颗以上麦粒的概率分别为0.5,0.15,0.1,0.05,求这批种子所结的穗含有50颗以上麦粒的概率.
解
设从这批种子中任选一颗是一等,二等,三等,四等种子的事件分别是A1,A2,A3,A4,则它们构成完备事件组,又设B表示任选一颗种子所结的穗含有50粒以上麦粒这一事件,则由全概率公式:
=95.5%×0.5+2%×0.15+1.5%×0.1+1%×0.05
=0.4825
【抽象概括】
设B1,B2,…,Bn为样本空间Ω的一个划分,若P(A)>0,P(Bi)>0(i=l,2,…,n),则
称上式为贝叶斯(Bayes)公式.
该公式于1763年由贝叶斯给出.它是在观察到事件人已发生的条件下,寻找导致人发生的每个原因的概率,贝叶斯公式的思想就是“执果溯因" .
例4 设验血诊断某种疾病的误诊率仅为5%,即若用A表示验血阳性,B表示受验者患病,则
若有10000人受检,患病者仅50人,其中验血阳性约47.5人
而9950健康人中,验血阳性者为9950×0.05=497.5人
变式1 设某工厂有甲、乙、丙三个车间生产同一种产品,已知各车间的产量分别占全厂产量的25 %, 35%, 40%,而且各车间的次品率依次为 5% ,4%, 2%.现从待出厂的产品中检查出一个次品,试判断它是由甲车间生产的概率.
解
设A1 ,A2 ,A3 分别表示产品由甲、乙、丙车间生产,B表示产品为次品. 显然,A1 ,A2 ,A3 构成完备事件组.依题意,有
P(A1)= 25% , P(A2)= 35% , P(A3)= 40%,
P(B|A1)= 5% , P(B|A2)=4% , P(B|A3)= 2%
P(A1|B)=
变式2 已知在所有男子中有5%,在所有女子中有0.25%患有色盲症。随机抽一人发现患色盲症,问其为男子的概率是多少?(设男子和女子的人数相等)。
解
设 A表示抽到的为男子,B表示抽到的是女子。
则
C表示抽到的人有色盲症。
由Bayes公式有
解:
1. 两批同种规格的产品,第一批占 40%,次品率为5%;第二批占60%,次品率为4%. 将两批产品混合,从混合产品中任取1件.
(1) 求这件产品是合格品的概率;
(2) 已知取到的是合格品,求它取自第一批产品的概率.
设A=“取到合格品”, Bi=“取到的产品来自第i批”(i=1, 2), 则
巩固练习
解:
2. 现有12道四选一 的单选题,学生张君对其中9道题有思路,3道题完全没有思路. 有思路的题做对的概率为0.9,没有思路的题只好任意猜一个答案,猜对答案的概率为0.25. 张君从这12道题中随机选择1题,求他做对该题的概率.
追问:若他做对了该题, 求他选择的是完全没有思路的题的概率.
*
4.在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干扰,发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.95和0.05. 假设发送信号0和1是等可能的.
(1) 分别求接收的信号为0和1的概率;
(2) 已知接收的信号为0,求发送的信号是1的概率.
发送0(A)
接收0(B)
4.在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干扰,发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.95和0.05. 假设发送信号0和1是等可能的.
(1) 分别求接收的信号为0和1的概率;
(2) 已知接收的信号为0,求发送的信号是1的概率.
解:
4.在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干扰,发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.95和0.05. 假设发送信号0和1是等可能的.
(1) 分别求接收的信号为0和1的概率;
(2) 已知接收的信号为0,求发送的信号是1的概率.
解:
P( A|B)
=
P( A)P(B| A)
P(B)
0.475
=
0.5×0.05
=
1
19
*
由因求果
执果寻因
1.设事件
2.写概率
3.代公式
全概率公式
P(B)=P(BA1)+P(BA2)+…+P(BAn)
=P(A1)P(B|A1)+P(A2)P(B|A2)+…+P(An)P(B|An)
条件概率P(B|A)= →
*贝叶斯公式
课堂小结
乘法公式P(AB)=P(A)P(B|A)
6.1.3全概率公式
温故知新
1. 条件概率:
在事件A发生的条件下,事件B发生的概率称为条件概率,即
由条件概率公式可得
2. 概率的乘法公式:
3. 条件概率的性质:
条设P(A)>0, 则
(1)P(Ω|A)=1;
(2)如果B和C是两个互斥事件, 则P(B∪C|A)=P(B|A)+P(C|A);
设A和B是两个独立事件, 则P(B|A)=P(B)或P(A|B)=P(A).
求复杂事件的概率常分成两个(或多个)互斥的较简单的事件之和的概率。
注意顺序!先发生的事件,写在前面
新课导入
在上节计算按对银行储蓄卡密码的概率时,我们首先把一个复杂事件表示为一些简单事件运算的结果,然后利用概率的加法和乘法公式求其概率。
本节,我们再根据一个求复杂事件概率问题出发学习。
解
引例
因为 B=AB +
,且AB与
互不相容,所以
= 0.6
一个盒子中有6只白球、4只黑球,从中不放回地每次任取1只,连取2次,求第二次取到白球的概率
例
A=“第一次取到白球” B=“第二次取到白球”
实例分析
如图,有三个箱子,分别编号为1,2,3,其中1号箱装有1个红球和4个白 球,2号箱装有2个红球和3个白球,3号箱装有3个红球,这些球除颜色外完全相同.某人先从三箱中任取一箱,再从中任意摸出一球,求取得红球的概率.
问题5
按照某种标准,将一个复杂事件表示为两个互斥事件的并,再由概率的加法公式和乘法公式求得这个复杂事件的概率.
【规律方法】
某电子设备制造厂所用的元件是由三家元件制造厂提供的,根据以往的记录 有如表的数据:
设这三家元件制造厂的元件在仓库中是均匀混合的,且无区别的标志.在仓库中随机地取一只元件,求它是次品的概率.
元件制造厂 次品率 提供元件的份额
1 0.02 0.15
2 0.01 0.80
3 0.03 0.05
问题6
分析 设事件Bi表示“所取到的产品是由第i家元件制造厂提供的”(i=1,2,3),事件A 表示“取到的是一件次品”.其中B1,B2,B3两两互斥,A发生总是伴随着 B1,B2,B3 之一同时发生.即A=B1A∪B2A ∪ B3A,且B1A,B2A,B3A两两互斥.运用互斥事件概率的加法公式和乘法公式,得 P(A) =P(B1A) +P(B2A) +P(B3A)
=F(B1)P(A|B1)+P(B2)P(A|B2)-P(B3)F(A|B3)
=0.15×0.02+ 0.80×0.01+0.05×0.03
=0.0125.
因此,在仓库中随机地取一只元件,它是次品的概率为0.0125.
从上述两个问题可以看出,某一事件A的发生有各种可能的原因,如问题1中摸得的红球有三种来源:可能取自1号箱,也可能取自2号箱或3号箱;问题2中取到的次品可能产自第1家元件制造厂,也可能产自第2家元件制造厂或第3家元件制造厂.若A是由原因 Bi(Bi=1,2,…n)所引起,则A发生的概率是
P(ABi)=P(Bi)P(A|Bi)
由于每一个原因都 可能导致A发生,且各原因涵盖所有可能的情形并彼此互斥,故事件A发生的概率是各原 因引起A发生概率的总和,即
设Ω是试验E的样本空间,B1,B2,…,Bn为样本空间的一组事件,若
(1)BiBj= ,其中i≠j(i,j=1,2,…,n),
(2)B1∪B2∪…∪Bn=Ω
则称B1,B2,…Bn为样本空间的一个划分.
条件(1)表示每次试验B1,B2,…Bn中只能发生一个;
条件(2)表示每次试验B1,B2,…Bn必有发生一个.
全概率公式
例1 釆购员要购买某种电器元件一包(10个).他的采购方法是:从一包中随机抽查 3个,如这3个元件都是好的,他才买下这一包.假定含有4个次品的包数占30%,而其余包中各含1个次品,求采购员随机挑选一包拒绝购买的概率.
从而由全概率公式,可知
因此,釆购员随机挑选一包
拒绝购买的概率为 .
变式: 某学校有 A,B两家餐厅,王同学第1天午餐时随机地选择一家餐厅用餐. 如果第1天去A餐厅,那么第2天去A餐厅的概率为0.6;如果第1天去B餐厅,那么第2天去A餐厅的概率为0.8. 计算王同学第2天去A餐厅用餐的概率.
设A1=“第1天去A餐厅”, B1=“第1天取B餐厅”, A2=“第2天去A餐厅”, 则
解:
例2 甲、乙、丙三人同时对飞机进行射击,三人击中的概率分别为0.4,0.5,0.7.飞机被一人击中且击落的概率为0.2,被两人击中且击落的概率为0.6,若三人都击中,飞机必定被击落,求飞机被击落的概率.
解 设事件A表示“飞机被击落”,事件Bi表示“飞机被i人击中”(i=0,1,2,3),则B0,构成样本空间的一个划分,且依题意,P(A|B0)=0,P(A|B1)=0.2,P(A|B2)=0.6, P(A|B3) = 1.
再设事件Hi表示“飞机被第i人击中”i=1,2,3).
则
同理
由全概率公式,可知
因此,飞机被击落的概率为0.458.
运用全概率公式的一般步骤如下:
(1)求出样本空间Ω的一个划分B1,B2,…,Bn;
(2)求P(Bi)(i=l,2,…,n);
(3)求P(A|Bi) (i=l,2,…,n);
(4)求目标事件的概率P(A).
可以形象地把全概率公式看成“由原因推结果”,每个原因对结果的发生有一定的“作用”,即结果发生的可能性与各种原因的“作用”大小有关.全概率公式表达了它们之间的关系.
总结
在实际中,还有一类问题是“已知结果求原因".这类问题更为常见,它所求的是条件概率,是已知某结果发生条件下,探求各原因发生的可能性大小.
例3 如图,有三个箱子,分别编号为1,2,3,其中 1号箱装有1个红球和4个白球,2号箱装有2个红球和3个白球,3号箱装有3个红球,这些球除颜色外完全相同.某人先从三箱中任取一箱,再从中任意摸出一球,发现是红球,求该球是取自1号箱的概率以及该球取自几号箱的可能性最大.
解设事件Bi表示“球取自i号箱”(i=1,2,3),
事件A表示“取得红球”.
由全概率公式,可得
P(A) = P(B1)F(A|B1)+F(B2)F(A|B2)+F(B3)P(A|B3)
再由条件概率知,
因此,该球是取自1号箱的概率为 ,该球取自3号箱的可能性最大.
解
= 0.6
变式1:一个盒子中有6只白球、4只黑球,从中不放回地每次任取1只,连取2次,求第二次取到白球的概率
A={第一次取到白球} B={第二次取到白球}
变式2: 商店销售一批收音机10台,其中3台次品,但是已经售出2台,问从剩下的收音机中,任取一台为正品的概率是多少
解: 设A1表示售出的两台均为正品,A2表示售出的两台为一件正品和一件次品,A3表示售出的两台均为次品,则A1,A2,A3是完备事件组.
设B表示从剩下的收音机中任取一台为正品,
变式3: 设播种用麦种中混有一等,二等,三等,四等四个等级的种子,分别各占95.5%,2%,1.5%,1%,用一等,二等,三等,四等种子长出的穗含50颗以上麦粒的概率分别为0.5,0.15,0.1,0.05,求这批种子所结的穗含有50颗以上麦粒的概率.
解
设从这批种子中任选一颗是一等,二等,三等,四等种子的事件分别是A1,A2,A3,A4,则它们构成完备事件组,又设B表示任选一颗种子所结的穗含有50粒以上麦粒这一事件,则由全概率公式:
=95.5%×0.5+2%×0.15+1.5%×0.1+1%×0.05
=0.4825
【抽象概括】
设B1,B2,…,Bn为样本空间Ω的一个划分,若P(A)>0,P(Bi)>0(i=l,2,…,n),则
称上式为贝叶斯(Bayes)公式.
该公式于1763年由贝叶斯给出.它是在观察到事件人已发生的条件下,寻找导致人发生的每个原因的概率,贝叶斯公式的思想就是“执果溯因" .
例4 设验血诊断某种疾病的误诊率仅为5%,即若用A表示验血阳性,B表示受验者患病,则
若有10000人受检,患病者仅50人,其中验血阳性约47.5人
而9950健康人中,验血阳性者为9950×0.05=497.5人
变式1 设某工厂有甲、乙、丙三个车间生产同一种产品,已知各车间的产量分别占全厂产量的25 %, 35%, 40%,而且各车间的次品率依次为 5% ,4%, 2%.现从待出厂的产品中检查出一个次品,试判断它是由甲车间生产的概率.
解
设A1 ,A2 ,A3 分别表示产品由甲、乙、丙车间生产,B表示产品为次品. 显然,A1 ,A2 ,A3 构成完备事件组.依题意,有
P(A1)= 25% , P(A2)= 35% , P(A3)= 40%,
P(B|A1)= 5% , P(B|A2)=4% , P(B|A3)= 2%
P(A1|B)=
变式2 已知在所有男子中有5%,在所有女子中有0.25%患有色盲症。随机抽一人发现患色盲症,问其为男子的概率是多少?(设男子和女子的人数相等)。
解
设 A表示抽到的为男子,B表示抽到的是女子。
则
C表示抽到的人有色盲症。
由Bayes公式有
解:
1. 两批同种规格的产品,第一批占 40%,次品率为5%;第二批占60%,次品率为4%. 将两批产品混合,从混合产品中任取1件.
(1) 求这件产品是合格品的概率;
(2) 已知取到的是合格品,求它取自第一批产品的概率.
设A=“取到合格品”, Bi=“取到的产品来自第i批”(i=1, 2), 则
巩固练习
解:
2. 现有12道四选一 的单选题,学生张君对其中9道题有思路,3道题完全没有思路. 有思路的题做对的概率为0.9,没有思路的题只好任意猜一个答案,猜对答案的概率为0.25. 张君从这12道题中随机选择1题,求他做对该题的概率.
追问:若他做对了该题, 求他选择的是完全没有思路的题的概率.
*
4.在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干扰,发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.95和0.05. 假设发送信号0和1是等可能的.
(1) 分别求接收的信号为0和1的概率;
(2) 已知接收的信号为0,求发送的信号是1的概率.
发送0(A)
接收0(B)
4.在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干扰,发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.95和0.05. 假设发送信号0和1是等可能的.
(1) 分别求接收的信号为0和1的概率;
(2) 已知接收的信号为0,求发送的信号是1的概率.
解:
4.在数字通信中,信号是由数字0和1组成的序列.由于随机因素的干扰,发送的信号0或1有可能被错误地接收为1或0.已知发送信号0时,接收为0和1的概率分别为0.9和0.1;发送信号1时,接收为1和0的概率分别为0.95和0.05. 假设发送信号0和1是等可能的.
(1) 分别求接收的信号为0和1的概率;
(2) 已知接收的信号为0,求发送的信号是1的概率.
解:
P( A|B)
=
P( A)P(B| A)
P(B)
0.475
=
0.5×0.05
=
1
19
*
由因求果
执果寻因
1.设事件
2.写概率
3.代公式
全概率公式
P(B)=P(BA1)+P(BA2)+…+P(BAn)
=P(A1)P(B|A1)+P(A2)P(B|A2)+…+P(An)P(B|An)
条件概率P(B|A)= →
*贝叶斯公式
课堂小结
乘法公式P(AB)=P(A)P(B|A)
同课章节目录
