北师大版高中数学选择性必修第一册 6.3.2离散型随机变量的方差 课件(共15张PPT)
文档属性
| 名称 | 北师大版高中数学选择性必修第一册 6.3.2离散型随机变量的方差 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 508.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 10:41:28 | ||
图片预览






文档简介
(共15张PPT)
6.3 第2课时
新授课
离散型随机变量的方差
均值能够反映随机变量取值的“平均水平”,但有时两个随机变量的均值相同,其取值却存在较大的差异,如何来研究这种差异呢?
1.通过实例理解离散型随机变量方差和标准差的含义,了解随机变量的方差与样本方差的区别与联系.
2.能计算简单离散型随机变量的方差.
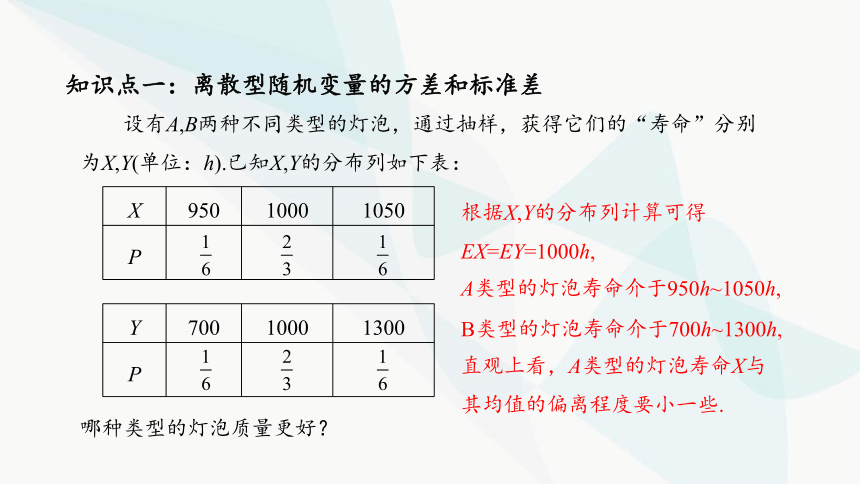
知识点一:离散型随机变量的方差和标准差
设有A,B两种不同类型的灯泡,通过抽样,获得它们的“寿命”分别为X,Y(单位:h).已知X,Y的分布列如下表:
X 950 1000 1050
P
Y 700 1000 1300
P
哪种类型的灯泡质量更好?
直观上看,A类型的灯泡寿命X与其均值的偏离程度要小一些.
根据X,Y的分布列计算可得EX=EY=1000h,
A类型的灯泡寿命介于950h~1050h,
B类型的灯泡寿命介于700h~1300h,
则 描述了xi(i=1,2,...,n)相对于均值EX的偏离程度,而
为这些偏离程度的加权平均,刻画了随机变量X与其均值EX的平均偏离程度.
称为DX为随机变量X的方差,其算术平方根 为随机变量X的标准差,记为 .
X x1 x2 … xi … xn
P p1 p2 … pi … pn
概念生成
若离散型随机变量X的分布列如表:
随机变量的方差DX和标准差 都反映了随机变量的取值偏离于均值的平均水平.
方差(标准差)越小,则随机变量偏离于均值的平均程度越小;
方差(标准差)越大,则随机变量的取值越分散.
注意点:
思考:根据以前所学知识,样本数据的离散程度是如何表示的?该如何定量刻画随机变量取值的离散程度?
随机变量的离散程度
样本数据的离散程度
(样本方差)
所有数据与样本均值的
“偏差平方的平均值”
可能取值与均值的
“偏差平方的平均值”
(随机变量的方差)
通过计算方差,标准差比较上面例子中哪种类型的灯泡质量更好.
X 950 1000 1050
P
Y 700 1000 1300
P
因为DX例1 随机抛掷一枚均匀的骰子,求掷出的点数X的方差和标准差(结果精确到0.01).
解:掷出点数X的分布列如表:
X 1 2 3 4 5 6
P
;
;
求离散型随机变量X的方差的基本步骤:
归纳总结
(1)理解X的意义,写出X可能取的全部值;
(2)求X取各个值的概率,写出分布列;
(3)根据分布列,由均值的定义求出EX;
(4)根据方差的定义求出DX.
A、B两台机床同时加工零件,每生产一批数量较大的产品时,产出次品的概率如下表所示:
问哪一台机床加工质量较好?
次品数ξ1 0 1 2 3
概率P 0.7 0.2 0.06 0.04
次品数ξ2 0 1 2 3
概率P 0.8 0.06 0.04 0.10
练一练
Eξ1=0×0.7+1×0.2+2×0.06+3×0.04=0.44,
Eξ2=0×0.8+1×0.06+2×0.04+3×0.10=0.44.
它们的期望相同,再比较它们的方差.
Dξ1=(0-0.44)2×0.7+(1-0.44)2×0.2+(2-0.44)2
×0.06+(3-0.44)2×0.04=0.6064,
Dξ2=(0-0.44)2×0.8+(1-0.44)2×0.06+(2-0.44)2
×0.04+(3-0.44)2×0.10=0.9264.
∴Dξ1< Dξ2 故A机床加工较稳定、质量较好.
解:
例2 甲、乙两名工人加工同一种零件,两人每天加工的零件数相等,设ξ,η分别表示甲、乙两人所加工出的次品件数,且ξ和η的分布列分别如表1和表2:
ξ 0 1 2
P
表1
表2
η 0 1 2
P
试比较这两名工人谁的技术水平更高.
解:因为
即Eξ=Eη,说明甲、乙两名工人所加工出的平均次品件数相同,可以认为他们的技术水平相当.
又因为
所以Dξ>Dη,说明工人乙的技术比较稳定.
根据今天所学,回答下列问题:
1.如何求离散型随机变量的方差?
2.随机变量的方差与样本方差的区别与联系?
3.求离散型随机变量X的方差的基本步骤是什么?
6.3 第2课时
新授课
离散型随机变量的方差
均值能够反映随机变量取值的“平均水平”,但有时两个随机变量的均值相同,其取值却存在较大的差异,如何来研究这种差异呢?
1.通过实例理解离散型随机变量方差和标准差的含义,了解随机变量的方差与样本方差的区别与联系.
2.能计算简单离散型随机变量的方差.
知识点一:离散型随机变量的方差和标准差
设有A,B两种不同类型的灯泡,通过抽样,获得它们的“寿命”分别为X,Y(单位:h).已知X,Y的分布列如下表:
X 950 1000 1050
P
Y 700 1000 1300
P
哪种类型的灯泡质量更好?
直观上看,A类型的灯泡寿命X与其均值的偏离程度要小一些.
根据X,Y的分布列计算可得EX=EY=1000h,
A类型的灯泡寿命介于950h~1050h,
B类型的灯泡寿命介于700h~1300h,
则 描述了xi(i=1,2,...,n)相对于均值EX的偏离程度,而
为这些偏离程度的加权平均,刻画了随机变量X与其均值EX的平均偏离程度.
称为DX为随机变量X的方差,其算术平方根 为随机变量X的标准差,记为 .
X x1 x2 … xi … xn
P p1 p2 … pi … pn
概念生成
若离散型随机变量X的分布列如表:
随机变量的方差DX和标准差 都反映了随机变量的取值偏离于均值的平均水平.
方差(标准差)越小,则随机变量偏离于均值的平均程度越小;
方差(标准差)越大,则随机变量的取值越分散.
注意点:
思考:根据以前所学知识,样本数据的离散程度是如何表示的?该如何定量刻画随机变量取值的离散程度?
随机变量的离散程度
样本数据的离散程度
(样本方差)
所有数据与样本均值的
“偏差平方的平均值”
可能取值与均值的
“偏差平方的平均值”
(随机变量的方差)
通过计算方差,标准差比较上面例子中哪种类型的灯泡质量更好.
X 950 1000 1050
P
Y 700 1000 1300
P
因为DX
解:掷出点数X的分布列如表:
X 1 2 3 4 5 6
P
;
;
求离散型随机变量X的方差的基本步骤:
归纳总结
(1)理解X的意义,写出X可能取的全部值;
(2)求X取各个值的概率,写出分布列;
(3)根据分布列,由均值的定义求出EX;
(4)根据方差的定义求出DX.
A、B两台机床同时加工零件,每生产一批数量较大的产品时,产出次品的概率如下表所示:
问哪一台机床加工质量较好?
次品数ξ1 0 1 2 3
概率P 0.7 0.2 0.06 0.04
次品数ξ2 0 1 2 3
概率P 0.8 0.06 0.04 0.10
练一练
Eξ1=0×0.7+1×0.2+2×0.06+3×0.04=0.44,
Eξ2=0×0.8+1×0.06+2×0.04+3×0.10=0.44.
它们的期望相同,再比较它们的方差.
Dξ1=(0-0.44)2×0.7+(1-0.44)2×0.2+(2-0.44)2
×0.06+(3-0.44)2×0.04=0.6064,
Dξ2=(0-0.44)2×0.8+(1-0.44)2×0.06+(2-0.44)2
×0.04+(3-0.44)2×0.10=0.9264.
∴Dξ1< Dξ2 故A机床加工较稳定、质量较好.
解:
例2 甲、乙两名工人加工同一种零件,两人每天加工的零件数相等,设ξ,η分别表示甲、乙两人所加工出的次品件数,且ξ和η的分布列分别如表1和表2:
ξ 0 1 2
P
表1
表2
η 0 1 2
P
试比较这两名工人谁的技术水平更高.
解:因为
即Eξ=Eη,说明甲、乙两名工人所加工出的平均次品件数相同,可以认为他们的技术水平相当.
又因为
所以Dξ>Dη,说明工人乙的技术比较稳定.
根据今天所学,回答下列问题:
1.如何求离散型随机变量的方差?
2.随机变量的方差与样本方差的区别与联系?
3.求离散型随机变量X的方差的基本步骤是什么?
同课章节目录
