北师大版高中数学选择性必修第一册 7.1一元线性回归 课件(共58张PPT)
文档属性
| 名称 | 北师大版高中数学选择性必修第一册 7.1一元线性回归 课件(共58张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 11:02:56 | ||
图片预览





文档简介
(共58张PPT)
7.1一元线性回归
在现实生活中,反映量与量之间的函数关系非常普遍,但也存在一些量与量之间不满足函数关系,如人的身高与体重.一般说来,人的身高越高,体重就越重,二者确实有关系.但是身高相同的人,体重却不一定相同,也就是说,给定身高h没有唯一的体重m与之对应.在现实生活中,这样的例子还有很多,如人的年龄与血压、农作物的施肥量与产量等.
实例分析
1.1直线拟合
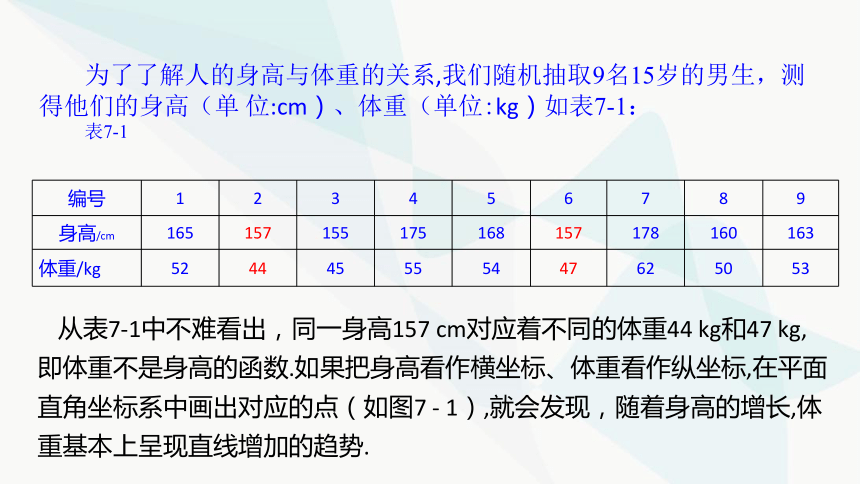
为了了解人的身高与体重的关系,我们随机抽取9名15岁的男生,测得他们的身高(单 位:cm)、体重(单位:kg)如表7-1:
表7-1
编号 1 2 3 4 5 6 7 8 9
身高/cm 165 157 155 175 168 157 178 160 163
体重/kg 52 44 45 55 54 47 62 50 53
从表7-1中不难看出,同一身高157 cm对应着不同的体重44 kg和47 kg,即体重不是身高的函数.如果把身高看作横坐标、体重看作纵坐标,在平面直角坐标系中画出对应的点(如图7 - 1),就会发现,随着身高的增长,体重基本上呈现直线增加的趋势.
1.在图7-1中,每个点对应的一对数据(xi, yi ),称为
成对数据.这些点构成的图称为散点图.
2.从散点图上可以看出,如果变量之间存在着某种
关系,这些点会有一个大致趋势,这种趋势通常可以用
一条光滑的曲线来近似地描述.这样近似描述的过程称为曲线拟合。
3.若在两个变量x和y的散点图中,所有点看上去都在一条直线附近波动,此时就可以用一条直线 来近似地描述这两个量之间的关系,称之为直线拟合.
那么,应当如何求出这条直线呢?
方法1 选取散点图中的两个点,使得其余的点在这两个点所连直线两侧分布得尽可能一样多,如有人选取了(165,52)和(168,54)这两个成对数据,得到直线方程为2x-3y-174 = 0.因此,一个身高166 cm的15岁男生,他的体重大致为52.667kg.
方法2 将所有的点分成两部分,一部分是身高在165 cm以下的,一部分是身高在 165 cm以上(含165 cm)的;然后每部分的点求一个平均点:165cm以下的身高、体重的平均数(取整近似)作为一个平均点,即(158,48),165 cm以上(含165 cm)的身高、体重的平均数(取整近似)作为另一个平均点,即(172,56);最后将这两点连接成一条直线,得到直线方程为4x-7y-296 = 0,因此,一个身高166 cm的15岁男生,他的体重大致为52.571 kg.
上面两种方法都有一定的道理.用方法1,若x=175 cm,则可计算 y≈58.667 kg;用方法2,若x=175 cm,则可计算y≈714 kg.每一种方法均与实际观测值有偏差.在实际应 用时,我们通常选择本章第1.2节中介绍的方法进行处理.
散点图说明
1.定义:
将两个变量所对应的点在平面直角坐标系中描出来, 这些点就组成了变量之间的一个图, 这种图叫散点图.
2.散点图的画法:
把成对的两个变量分别作为横坐标和纵坐标, 把每对数值对应的点在平面直角坐标系中画出来.
3.散点图的作用:
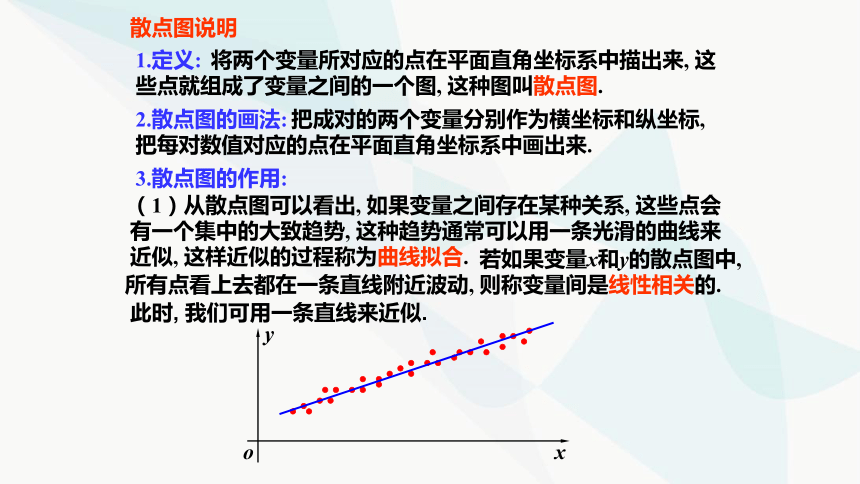
(1)从散点图可以看出, 如果变量之间存在某种关系, 这些点会有一个集中的大致趋势, 这种趋势通常可以用一条光滑的曲线来近似, 这样近似的过程称为曲线拟合.
若如果变量x和y的散点图中, 所有点看上去都在一条直线附近波动, 则称变量间是线性相关的.
此时, 我们可用一条直线来近似.
x
y
o
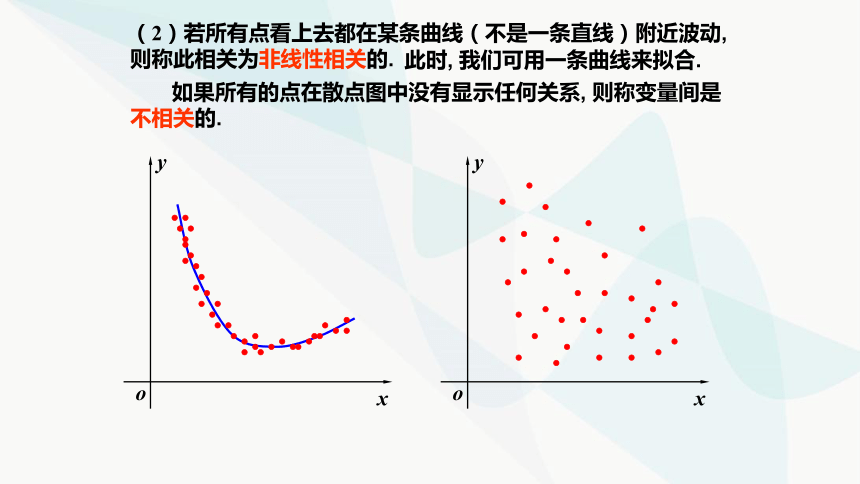
(2)若所有点看上去都在某条曲线(不是一条直线)附近波动, 则称此相关为非线性相关的.
此时, 我们可用一条曲线来拟合.
如果所有的点在散点图中没有显示任何关系, 则称变量间是不相关的.
x
y
o
x
y
o
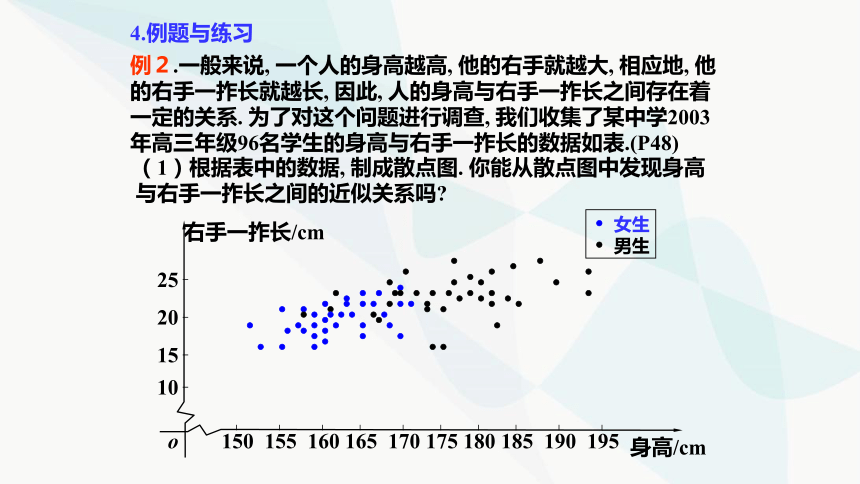
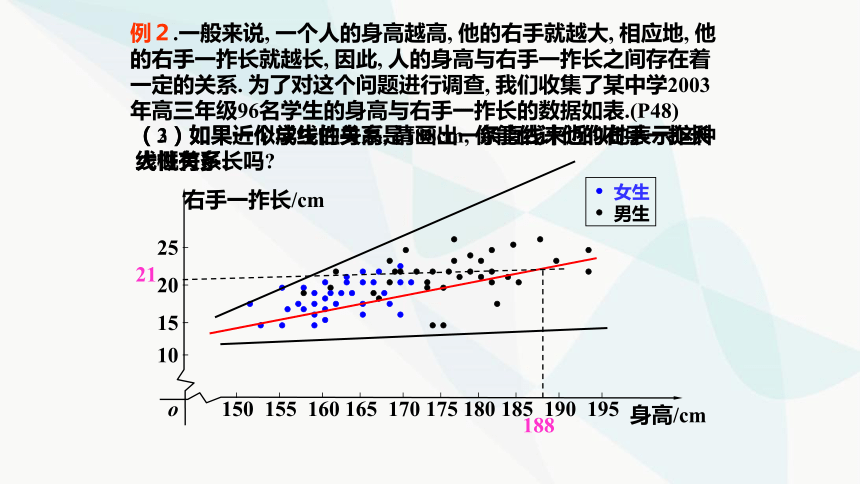
例2.一般来说, 一个人的身高越高, 他的右手就越大, 相应地, 他的右手一拃长就越长, 因此, 人的身高与右手一拃长之间存在着一定的关系. 为了对这个问题进行调查, 我们收集了某中学2003年高三年级96名学生的身高与右手一拃长的数据如表.(P48)
(1)根据表中的数据, 制成散点图. 你能从散点图中发现身高与右手一拃长之间的近似关系吗
o
身高/cm
右手一拃长/cm
150
155
160
165
170
175
180
185
190
195
10
15
20
25
女生
男生
4.例题与练习
例2.一般来说, 一个人的身高越高, 他的右手就越大, 相应地, 他的右手一拃长就越长, 因此, 人的身高与右手一拃长之间存在着一定的关系. 为了对这个问题进行调查, 我们收集了某中学2003年高三年级96名学生的身高与右手一拃长的数据如表.(P48)
(2)如果近似成线性关系, 请画出一条直线来近似地表示这种线性关系.
女生
男生
o
身高/cm
右手一拃长/cm
150
155
160
165
170
175
180
185
190
195
10
15
20
25
(3)如果一个学生的身高是188cm, 你能估计他的右手一拃长大概有多长吗
188
21
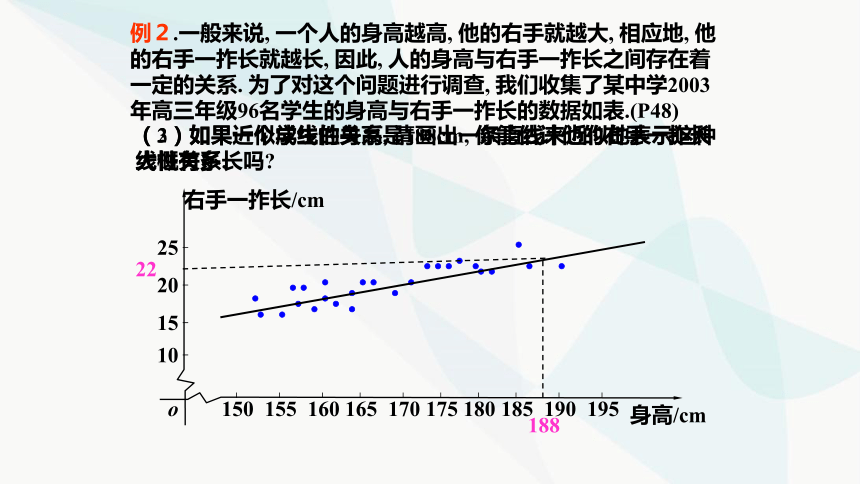
例2.一般来说, 一个人的身高越高, 他的右手就越大, 相应地, 他的右手一拃长就越长, 因此, 人的身高与右手一拃长之间存在着一定的关系. 为了对这个问题进行调查, 我们收集了某中学2003年高三年级96名学生的身高与右手一拃长的数据如表.(P48)
(2)如果近似成线性关系, 请画出一条直线来近似地表示这种线性关系.
o
身高/cm
右手一拃长/cm
150
155
160
165
170
175
180
185
190
195
10
15
20
25
(3)如果一个学生的身高是188cm, 你能估计他的右手一拃长大概有多长吗
188
22
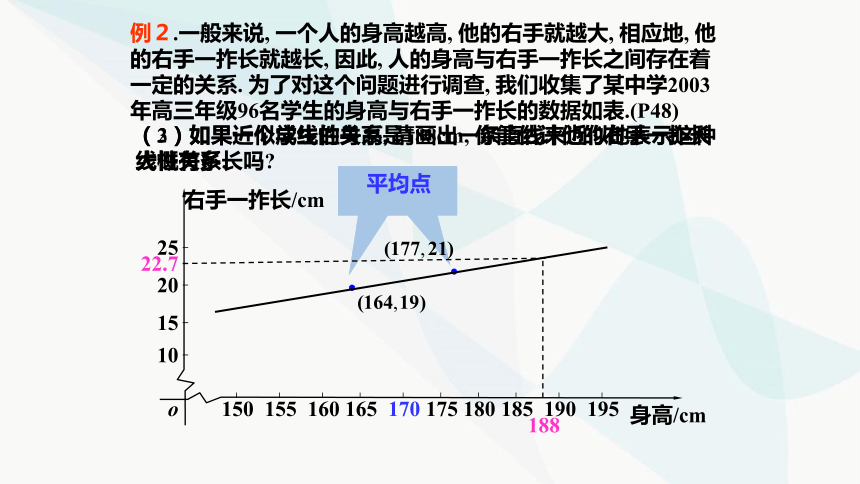
平均点
例2.一般来说, 一个人的身高越高, 他的右手就越大, 相应地, 他的右手一拃长就越长, 因此, 人的身高与右手一拃长之间存在着一定的关系. 为了对这个问题进行调查, 我们收集了某中学2003年高三年级96名学生的身高与右手一拃长的数据如表.(P48)
(2)如果近似成线性关系, 请画出一条直线来近似地表示这种线性关系.
o
身高/cm
右手一拃长/cm
150
155
160
165
170
175
180
185
190
195
10
15
20
25
(3)如果一个学生的身高是188cm, 你能估计他的右手一拃长大概有多长吗
188
22.7
例.一般来说, 一个人的身高越高, 他的右手就越大, 相应地, 他的右手一拃长就越长, 因此, 人的身高与右手一拃长之间存在着一定的关系. 为了对这个问题进行调查, 我们收集了某中学2003年高三年级96名学生的身高与右手一拃长的数据如表.(P48)
(3)如果一个学生的身高是188cm, 你能估计他的右手一拃长大概有多长吗
o
身高/cm
右手一拃长/cm
160
18.0
162
180
166
168
170
172
174
176
178
164
182
18.5
19.0
19.5
20.0
20.5
21.0
21.5
(2)如果近似成线性关系, 请画出一条直线来近似地表示这种线性关系.
例1 某种木材体积与树木的树龄之间有如下的对应关系:
(1)请作出这些数据的散点图;
树龄 2 3 4 5 6 7 8
体积 30 34 40 60 55 62 70
解 以x轴表示树木的树龄,y轴表示树木的体积,可得相应的散点图如图所示:
(2)你能由散点图发现木材体积与树木的树龄近似成什么关系吗?
解 由散点图发现木材体积随着树龄的增加而呈增加的趋势,且散点落在一条直线附近,所以木材的体积与树龄成线性关系.
练习: 以下四个散点图中,两个变量的关系适合用直线拟合描述的是( )
A.①② B.①③ C.②③ D.③④
解析 ①③中的点分布在一条直线附近,适合直线拟合描述.
B
例2 某品牌服装的广告费支出x(单位:万元)与销售额y(单位:万元)之间有如下的对应数据:
广告费支出x 2 4 6 8 10
销售额y 64 138 205 285 360
(1)试画出散点图,并判断广告费支出x与销售额y是否具有线性相关关系;
(2)若取过点(2,64)和点(8,285)的直线作为拟合直线,试预测当x=10和15时销售额y的值是多少?(结果保留一位小数)
解 (1)根据题中数据画出散点图如图
观察散点图,可以发现5个样本点从整体上看大致在一条直线附近,所以变量x,y之间具有线性相关关系.
(2)过点(2,64)和点(8,285)的直线方程是221x-6y-58=0.
令x=10,则221×10-6y-58=0,∴ y≈358.7;
令x=15,则221×15-6y-58=0,∴ y≈542.8,
即当x=10时,销售额y的值大约是358.7万元;当x=15时,销售额y的值大约是542.8万元.
反思 利用拟合直线进行预测时应注意的问题
(1)首先要理解线性相关和拟合直线方程的意义.
(2)利用拟合直线方程求得的预测值只是实际问题的一个估计值,因此在回答结论时不能说成是准确值,而只能用“大约”等词来回答.
1.2 一元线性回归方程
对于给定的两个变量x和y(如身高和体重),可以把其成对的观测值(x1,y1),(x2,y2),…,(xn,yn)表示为平面直角坐标系中的n个点.
现在希望找到一条直线Y = a +bX,使得对每一个xi(i=1,2, …,n),由这个直线方程计算出来的值a+bi与实际观测值yi的差异尽可能小.为此,希望
[y1-(a+b1)]2+[y2-(a+b2)]2+…+[yn-(a+bn)]2达到最小.换句话说,我们希望a,b的取值能使上式达到最小.这个方法称为最小二乘法.
为了直观起见,先考虑3对数据(x1,y1),(x2,y2),(x3,y3),即:求a,b的值,使得偏差yi-(a+bi)(i= 1,2,3)的平方和最小,即[y1-(a+b1)]2+[y2-(a+b2)]2+[y3-(a+b3)]2达到最小.下面我们用向量的方法解决这个问题.首先,用向量的语言描述问题.
要用向量的语言描述偏差yi-(a+bi)(i= 1,2,3),容易想到将偏差作为向量的分量, 即向量的坐标(y1-(a+b1),y2-(a+b2),y3-(a+b3)).这样,问题就等价于:求的a,b值,使得向量
(y1-(a+b1),y2-(a+b2),y3-(a+b3))的长度最小.
在这里需要强调的是:身高和体重之间并没有函数关系,我们得到的线性回归方程只是对其变化趋势的一种近似描述.对一个给定身高的人,人们可以用这个方程来估计这个人的体重,这是十分有意义的.
…………………①
先来讨论3个样本点的情况
补充:怎样使
达到最小值?
函数法求线性回归方程:
利用配方法可得
同样使用配方法可以得到,当
假设我们已经得到两个具有相关关系的变量的一组数据
且回归方程是:y=bx+a,
^
其中,a,b是待定参数。当变量x取 时
它与实际收集到的 之间的偏差是
o
x
y
www.
*
易知,截距 和斜率 分别是使
取最小值时 的值。由于
这正是我们所要推导的公式。
在上式中,后两项和 无关,而前两项为非负数,因此要使Q取得最小值,当且仅当前两项的值均为0,即有
*
*
用同样的方法我们可以推导出n个点的线性回归方程的系数:
牢记公式
1、所求直线方程叫做回归直线方程;
相应的直线叫做回归直线。
2、对两个变量进行的线性分析叫做线性回归分析。
回归直线方程
最小二乘法:
称为样本点的中心。
www.
2、求回归直线方程的步骤:
(3)代入公式
(4)写出直线方程为y=bx+a,即为所求的回归直线方程。
^
例1 在本章1.1节的练习中,从散点图可以看出,某小卖部6天卖出热茶的杯数Y(单位:杯)与当天气温X(单位:°C)之间存在近似的线性关系.数据如表7-2.
(1)试用最小二乘法求岀Y关于X的线性回归方程;
(2)如果某天的气温是-3℃,请预测这天可能会
卖出热茶多少杯.
1.思考辨析(正确的画“√”,错误的画“×”)
(1)利用散点图可以直观判断两个变量的关系是否可以用线性表示.( )
(2)线性回归方程适用于一切样本和总体.( )
(3)线性回归方程一般都有局限性.( )
(4)线性回归方程一定过样本中的某一点.( )
√
×
√
×
巩固提升
2.如果记录了x,y的几组数据分别为(0,1),(1,3),(2,5),(3,7),那么y关于x的线性回归直线必过点( )
A.(2,2) B.(1.5,2) C.(1,2) D.(1.5,4)
答案:D
3.随机抽样中测得四个样本点为(1,2),(2,3),(3,4),(4,5),则y与x之间的线性回归方程为( )
A.y=x+1 B.y=x+2
C.y=2x+1 D.y=x-1
答案:A
例3 在本章1.1节的练习中,从散点图可以看出,某小卖部6天卖出热茶的杯数Y(单位:杯)与当天气温X(单位:°C)之间存在近似的线性关系.数据如表7-2.
(1) 试用最小二乘法求岀Y关于X的线性回归方程;
(2) 如果某天的气温是-3℃,请预测这天可能会
卖出热茶多少杯.
解(1)从散点图7-6中可以看岀,表7-2中的两
个变量有近似的线性关系.
例4 某项研究发现某地的PM10浓度与车流量之间有线性相关关系.现采集到该地一周内车流量x与PM10浓度y的数据如下表:
时间 车流量x(单位:万辆) PM10浓度y(单位:μg/m3)
星期一 25.4 35.7
星期二 24.6 34.5
星期三 23.5 35.2
星期四 24.4 33.6
星期五 25.8 36.1
星期六 19.7 30.9
星期日 20.3 29.4
解析:(1)如图所示.
月份代码t 1 2 3 4 5 6 7
销售量y(万件) y1 y2 y3 y4 y5 y6 y7
例5 某地区2013年至2019年农村居民家庭人均纯收入Y(单位:千元)的数据如下表:
(1)求Y关于T的线性回归方程;
年份 2013 2014 2015 2016 2017 2018 2019
年份代号T 1 2 3 4 5 6 7
人均纯收入Y 2.9 3.3 3.6 4.4 4.8 5.2 5.9
解 由所给数据计算得
=(-3)×(-1.4)+(-2)×(-1)+(-1)×(-0.7)+0×0.1+1×0.5+2×0.9+3×1.6=14,
所求线性回归方程为Y=0.5T+2.3.
(2)利用(1)中的线性回归方程,分析2013年至2019年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2022年农村居民家庭人均纯收入.
解 由(1)知, =0.5>0,故2013年至2019年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.
将2022年的年份代号代入(1)中的线性回归方程,得0.5×10+2.3=7.3,
故预测该地区2022年农村居民家庭人均纯收入为7.3千元.
反思感悟 (1)解决问题时应首先对X,Y进行相关性检验,如果两个变量之间本身不具有相关关系或者它们之间的相关关系不显著,即使求出线性回归方程进行估计和预测的量也是不可信的.
x 0 1 2 3
y 1 3 5 7
D
1.已知x,y之间的一组数据如下表,则y与x的线性回归方程y=a+bx必经过点 ( )
A.(2,2) B.(1.5,0) C.(1,2) D.(1.5,4)
A
A
4.某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
(1)画出销售额和利润额的散点图.
(2)若销售额和利润额具有相关关系,计算利润额y对销售额x的线性回归方程.
商店名称 A B C D E
销售额(x)/千万元 3 5 6 7 9
利润额(y)/百万元 2 3 3 4 5
i xi yi xi2 xiyi
1 3 2 9 6
2 5 3 25 15
3 6 3 36 18
4 7 4 49 28
5 9 5 81 45
合计 30 17 200 112
(2)数据如下表:可以求得b=0.5,a=0.4
线性回归方程为:
/千万元
解:(1)
/百万元
(1)散点图如图所示:
2.线性回归方程的系数:
1.最小二乘法的思想.
7.1一元线性回归
在现实生活中,反映量与量之间的函数关系非常普遍,但也存在一些量与量之间不满足函数关系,如人的身高与体重.一般说来,人的身高越高,体重就越重,二者确实有关系.但是身高相同的人,体重却不一定相同,也就是说,给定身高h没有唯一的体重m与之对应.在现实生活中,这样的例子还有很多,如人的年龄与血压、农作物的施肥量与产量等.
实例分析
1.1直线拟合
为了了解人的身高与体重的关系,我们随机抽取9名15岁的男生,测得他们的身高(单 位:cm)、体重(单位:kg)如表7-1:
表7-1
编号 1 2 3 4 5 6 7 8 9
身高/cm 165 157 155 175 168 157 178 160 163
体重/kg 52 44 45 55 54 47 62 50 53
从表7-1中不难看出,同一身高157 cm对应着不同的体重44 kg和47 kg,即体重不是身高的函数.如果把身高看作横坐标、体重看作纵坐标,在平面直角坐标系中画出对应的点(如图7 - 1),就会发现,随着身高的增长,体重基本上呈现直线增加的趋势.
1.在图7-1中,每个点对应的一对数据(xi, yi ),称为
成对数据.这些点构成的图称为散点图.
2.从散点图上可以看出,如果变量之间存在着某种
关系,这些点会有一个大致趋势,这种趋势通常可以用
一条光滑的曲线来近似地描述.这样近似描述的过程称为曲线拟合。
3.若在两个变量x和y的散点图中,所有点看上去都在一条直线附近波动,此时就可以用一条直线 来近似地描述这两个量之间的关系,称之为直线拟合.
那么,应当如何求出这条直线呢?
方法1 选取散点图中的两个点,使得其余的点在这两个点所连直线两侧分布得尽可能一样多,如有人选取了(165,52)和(168,54)这两个成对数据,得到直线方程为2x-3y-174 = 0.因此,一个身高166 cm的15岁男生,他的体重大致为52.667kg.
方法2 将所有的点分成两部分,一部分是身高在165 cm以下的,一部分是身高在 165 cm以上(含165 cm)的;然后每部分的点求一个平均点:165cm以下的身高、体重的平均数(取整近似)作为一个平均点,即(158,48),165 cm以上(含165 cm)的身高、体重的平均数(取整近似)作为另一个平均点,即(172,56);最后将这两点连接成一条直线,得到直线方程为4x-7y-296 = 0,因此,一个身高166 cm的15岁男生,他的体重大致为52.571 kg.
上面两种方法都有一定的道理.用方法1,若x=175 cm,则可计算 y≈58.667 kg;用方法2,若x=175 cm,则可计算y≈714 kg.每一种方法均与实际观测值有偏差.在实际应 用时,我们通常选择本章第1.2节中介绍的方法进行处理.
散点图说明
1.定义:
将两个变量所对应的点在平面直角坐标系中描出来, 这些点就组成了变量之间的一个图, 这种图叫散点图.
2.散点图的画法:
把成对的两个变量分别作为横坐标和纵坐标, 把每对数值对应的点在平面直角坐标系中画出来.
3.散点图的作用:
(1)从散点图可以看出, 如果变量之间存在某种关系, 这些点会有一个集中的大致趋势, 这种趋势通常可以用一条光滑的曲线来近似, 这样近似的过程称为曲线拟合.
若如果变量x和y的散点图中, 所有点看上去都在一条直线附近波动, 则称变量间是线性相关的.
此时, 我们可用一条直线来近似.
x
y
o
(2)若所有点看上去都在某条曲线(不是一条直线)附近波动, 则称此相关为非线性相关的.
此时, 我们可用一条曲线来拟合.
如果所有的点在散点图中没有显示任何关系, 则称变量间是不相关的.
x
y
o
x
y
o
例2.一般来说, 一个人的身高越高, 他的右手就越大, 相应地, 他的右手一拃长就越长, 因此, 人的身高与右手一拃长之间存在着一定的关系. 为了对这个问题进行调查, 我们收集了某中学2003年高三年级96名学生的身高与右手一拃长的数据如表.(P48)
(1)根据表中的数据, 制成散点图. 你能从散点图中发现身高与右手一拃长之间的近似关系吗
o
身高/cm
右手一拃长/cm
150
155
160
165
170
175
180
185
190
195
10
15
20
25
女生
男生
4.例题与练习
例2.一般来说, 一个人的身高越高, 他的右手就越大, 相应地, 他的右手一拃长就越长, 因此, 人的身高与右手一拃长之间存在着一定的关系. 为了对这个问题进行调查, 我们收集了某中学2003年高三年级96名学生的身高与右手一拃长的数据如表.(P48)
(2)如果近似成线性关系, 请画出一条直线来近似地表示这种线性关系.
女生
男生
o
身高/cm
右手一拃长/cm
150
155
160
165
170
175
180
185
190
195
10
15
20
25
(3)如果一个学生的身高是188cm, 你能估计他的右手一拃长大概有多长吗
188
21
例2.一般来说, 一个人的身高越高, 他的右手就越大, 相应地, 他的右手一拃长就越长, 因此, 人的身高与右手一拃长之间存在着一定的关系. 为了对这个问题进行调查, 我们收集了某中学2003年高三年级96名学生的身高与右手一拃长的数据如表.(P48)
(2)如果近似成线性关系, 请画出一条直线来近似地表示这种线性关系.
o
身高/cm
右手一拃长/cm
150
155
160
165
170
175
180
185
190
195
10
15
20
25
(3)如果一个学生的身高是188cm, 你能估计他的右手一拃长大概有多长吗
188
22
平均点
例2.一般来说, 一个人的身高越高, 他的右手就越大, 相应地, 他的右手一拃长就越长, 因此, 人的身高与右手一拃长之间存在着一定的关系. 为了对这个问题进行调查, 我们收集了某中学2003年高三年级96名学生的身高与右手一拃长的数据如表.(P48)
(2)如果近似成线性关系, 请画出一条直线来近似地表示这种线性关系.
o
身高/cm
右手一拃长/cm
150
155
160
165
170
175
180
185
190
195
10
15
20
25
(3)如果一个学生的身高是188cm, 你能估计他的右手一拃长大概有多长吗
188
22.7
例.一般来说, 一个人的身高越高, 他的右手就越大, 相应地, 他的右手一拃长就越长, 因此, 人的身高与右手一拃长之间存在着一定的关系. 为了对这个问题进行调查, 我们收集了某中学2003年高三年级96名学生的身高与右手一拃长的数据如表.(P48)
(3)如果一个学生的身高是188cm, 你能估计他的右手一拃长大概有多长吗
o
身高/cm
右手一拃长/cm
160
18.0
162
180
166
168
170
172
174
176
178
164
182
18.5
19.0
19.5
20.0
20.5
21.0
21.5
(2)如果近似成线性关系, 请画出一条直线来近似地表示这种线性关系.
例1 某种木材体积与树木的树龄之间有如下的对应关系:
(1)请作出这些数据的散点图;
树龄 2 3 4 5 6 7 8
体积 30 34 40 60 55 62 70
解 以x轴表示树木的树龄,y轴表示树木的体积,可得相应的散点图如图所示:
(2)你能由散点图发现木材体积与树木的树龄近似成什么关系吗?
解 由散点图发现木材体积随着树龄的增加而呈增加的趋势,且散点落在一条直线附近,所以木材的体积与树龄成线性关系.
练习: 以下四个散点图中,两个变量的关系适合用直线拟合描述的是( )
A.①② B.①③ C.②③ D.③④
解析 ①③中的点分布在一条直线附近,适合直线拟合描述.
B
例2 某品牌服装的广告费支出x(单位:万元)与销售额y(单位:万元)之间有如下的对应数据:
广告费支出x 2 4 6 8 10
销售额y 64 138 205 285 360
(1)试画出散点图,并判断广告费支出x与销售额y是否具有线性相关关系;
(2)若取过点(2,64)和点(8,285)的直线作为拟合直线,试预测当x=10和15时销售额y的值是多少?(结果保留一位小数)
解 (1)根据题中数据画出散点图如图
观察散点图,可以发现5个样本点从整体上看大致在一条直线附近,所以变量x,y之间具有线性相关关系.
(2)过点(2,64)和点(8,285)的直线方程是221x-6y-58=0.
令x=10,则221×10-6y-58=0,∴ y≈358.7;
令x=15,则221×15-6y-58=0,∴ y≈542.8,
即当x=10时,销售额y的值大约是358.7万元;当x=15时,销售额y的值大约是542.8万元.
反思 利用拟合直线进行预测时应注意的问题
(1)首先要理解线性相关和拟合直线方程的意义.
(2)利用拟合直线方程求得的预测值只是实际问题的一个估计值,因此在回答结论时不能说成是准确值,而只能用“大约”等词来回答.
1.2 一元线性回归方程
对于给定的两个变量x和y(如身高和体重),可以把其成对的观测值(x1,y1),(x2,y2),…,(xn,yn)表示为平面直角坐标系中的n个点.
现在希望找到一条直线Y = a +bX,使得对每一个xi(i=1,2, …,n),由这个直线方程计算出来的值a+bi与实际观测值yi的差异尽可能小.为此,希望
[y1-(a+b1)]2+[y2-(a+b2)]2+…+[yn-(a+bn)]2达到最小.换句话说,我们希望a,b的取值能使上式达到最小.这个方法称为最小二乘法.
为了直观起见,先考虑3对数据(x1,y1),(x2,y2),(x3,y3),即:求a,b的值,使得偏差yi-(a+bi)(i= 1,2,3)的平方和最小,即[y1-(a+b1)]2+[y2-(a+b2)]2+[y3-(a+b3)]2达到最小.下面我们用向量的方法解决这个问题.首先,用向量的语言描述问题.
要用向量的语言描述偏差yi-(a+bi)(i= 1,2,3),容易想到将偏差作为向量的分量, 即向量的坐标(y1-(a+b1),y2-(a+b2),y3-(a+b3)).这样,问题就等价于:求的a,b值,使得向量
(y1-(a+b1),y2-(a+b2),y3-(a+b3))的长度最小.
在这里需要强调的是:身高和体重之间并没有函数关系,我们得到的线性回归方程只是对其变化趋势的一种近似描述.对一个给定身高的人,人们可以用这个方程来估计这个人的体重,这是十分有意义的.
…………………①
先来讨论3个样本点的情况
补充:怎样使
达到最小值?
函数法求线性回归方程:
利用配方法可得
同样使用配方法可以得到,当
假设我们已经得到两个具有相关关系的变量的一组数据
且回归方程是:y=bx+a,
^
其中,a,b是待定参数。当变量x取 时
它与实际收集到的 之间的偏差是
o
x
y
www.
*
易知,截距 和斜率 分别是使
取最小值时 的值。由于
这正是我们所要推导的公式。
在上式中,后两项和 无关,而前两项为非负数,因此要使Q取得最小值,当且仅当前两项的值均为0,即有
*
*
用同样的方法我们可以推导出n个点的线性回归方程的系数:
牢记公式
1、所求直线方程叫做回归直线方程;
相应的直线叫做回归直线。
2、对两个变量进行的线性分析叫做线性回归分析。
回归直线方程
最小二乘法:
称为样本点的中心。
www.
2、求回归直线方程的步骤:
(3)代入公式
(4)写出直线方程为y=bx+a,即为所求的回归直线方程。
^
例1 在本章1.1节的练习中,从散点图可以看出,某小卖部6天卖出热茶的杯数Y(单位:杯)与当天气温X(单位:°C)之间存在近似的线性关系.数据如表7-2.
(1)试用最小二乘法求岀Y关于X的线性回归方程;
(2)如果某天的气温是-3℃,请预测这天可能会
卖出热茶多少杯.
1.思考辨析(正确的画“√”,错误的画“×”)
(1)利用散点图可以直观判断两个变量的关系是否可以用线性表示.( )
(2)线性回归方程适用于一切样本和总体.( )
(3)线性回归方程一般都有局限性.( )
(4)线性回归方程一定过样本中的某一点.( )
√
×
√
×
巩固提升
2.如果记录了x,y的几组数据分别为(0,1),(1,3),(2,5),(3,7),那么y关于x的线性回归直线必过点( )
A.(2,2) B.(1.5,2) C.(1,2) D.(1.5,4)
答案:D
3.随机抽样中测得四个样本点为(1,2),(2,3),(3,4),(4,5),则y与x之间的线性回归方程为( )
A.y=x+1 B.y=x+2
C.y=2x+1 D.y=x-1
答案:A
例3 在本章1.1节的练习中,从散点图可以看出,某小卖部6天卖出热茶的杯数Y(单位:杯)与当天气温X(单位:°C)之间存在近似的线性关系.数据如表7-2.
(1) 试用最小二乘法求岀Y关于X的线性回归方程;
(2) 如果某天的气温是-3℃,请预测这天可能会
卖出热茶多少杯.
解(1)从散点图7-6中可以看岀,表7-2中的两
个变量有近似的线性关系.
例4 某项研究发现某地的PM10浓度与车流量之间有线性相关关系.现采集到该地一周内车流量x与PM10浓度y的数据如下表:
时间 车流量x(单位:万辆) PM10浓度y(单位:μg/m3)
星期一 25.4 35.7
星期二 24.6 34.5
星期三 23.5 35.2
星期四 24.4 33.6
星期五 25.8 36.1
星期六 19.7 30.9
星期日 20.3 29.4
解析:(1)如图所示.
月份代码t 1 2 3 4 5 6 7
销售量y(万件) y1 y2 y3 y4 y5 y6 y7
例5 某地区2013年至2019年农村居民家庭人均纯收入Y(单位:千元)的数据如下表:
(1)求Y关于T的线性回归方程;
年份 2013 2014 2015 2016 2017 2018 2019
年份代号T 1 2 3 4 5 6 7
人均纯收入Y 2.9 3.3 3.6 4.4 4.8 5.2 5.9
解 由所给数据计算得
=(-3)×(-1.4)+(-2)×(-1)+(-1)×(-0.7)+0×0.1+1×0.5+2×0.9+3×1.6=14,
所求线性回归方程为Y=0.5T+2.3.
(2)利用(1)中的线性回归方程,分析2013年至2019年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2022年农村居民家庭人均纯收入.
解 由(1)知, =0.5>0,故2013年至2019年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.
将2022年的年份代号代入(1)中的线性回归方程,得0.5×10+2.3=7.3,
故预测该地区2022年农村居民家庭人均纯收入为7.3千元.
反思感悟 (1)解决问题时应首先对X,Y进行相关性检验,如果两个变量之间本身不具有相关关系或者它们之间的相关关系不显著,即使求出线性回归方程进行估计和预测的量也是不可信的.
x 0 1 2 3
y 1 3 5 7
D
1.已知x,y之间的一组数据如下表,则y与x的线性回归方程y=a+bx必经过点 ( )
A.(2,2) B.(1.5,0) C.(1,2) D.(1.5,4)
A
A
4.某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
(1)画出销售额和利润额的散点图.
(2)若销售额和利润额具有相关关系,计算利润额y对销售额x的线性回归方程.
商店名称 A B C D E
销售额(x)/千万元 3 5 6 7 9
利润额(y)/百万元 2 3 3 4 5
i xi yi xi2 xiyi
1 3 2 9 6
2 5 3 25 15
3 6 3 36 18
4 7 4 49 28
5 9 5 81 45
合计 30 17 200 112
(2)数据如下表:可以求得b=0.5,a=0.4
线性回归方程为:
/千万元
解:(1)
/百万元
(1)散点图如图所示:
2.线性回归方程的系数:
1.最小二乘法的思想.
同课章节目录
