北师大版高中数学选择性必修第一册 7.2成对数据的线性相关性 课件(共60张PPT)
文档属性
| 名称 | 北师大版高中数学选择性必修第一册 7.2成对数据的线性相关性 课件(共60张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 00:00:00 | ||
图片预览









文档简介
(共60张PPT)
7.2成对数据的线性相关性
1、所求直线方程叫做回归直线方程;
相应的直线叫做回归直线。
2、对两个变量进行的线性分析叫做线性回归分析。
回归直线方程
温故知新
最小二乘法:
称为样本点的中心。
www.
温故知新
2、求回归直线方程的步骤:
(3)代入公式
(4)写出直线方程为y=bx+a,即为所求的回归直线方程。
^
温故知新
我们知道,如果变量 y 是变量 x 的函数,那么由 x 就可以唯一确定 y. 然而,现实世界中还存在这样的情况:两个变量之间有关系,但密切程度又达不到函数关系的程度. 例如,人的体重与身高存在关系,但由一个人的身高并不能确定他的体重值. 那么,该如何刻画这两个变量之间的关系呢?下面我们就来研究这个问题.
引入新课
我们知道,一个人的体重与他的身高有关系. 一般而言,个子高的人往往体重值较大,个子矮的人往往体重值较小. 但身高并不是决定体重的唯一因素,例如生活中的饮食习惯、体育锻炼、睡眠时间以及遗传因素等也是影响体重的重要因素. 像这样,两个变量有关系,但又没有确切到可由其中一个去精确地决定另一个的程度,这种关系称为相关关系.
变量的相关关系
两个变量具有相关关系的事例在现实中大量存在. 例如:
1.子女身高 y 与父亲身高 x 之间的关系;
2.商品销售收入 y 与广告支出 x 之间的关系;
3.空气污染指数 y 与汽车保有量 x 之间的关系;
4.粮食亩产量 y 与施肥量 x 之间的关系.
对上述各例中两个变量之间的相关关系,我们往往会根据自己以往积累的经验作出推断. “经验之中有规律”,经验的确可以为我们的决策提供一定的依据,但仅凭经验推断又有不足.
因为在相关关系中,变量 y 的值不能随变量 x 的值的确定而唯一确定,所以我们无法直接用函数去描述变量之间的这种关系. 因此,在研究两个变量之间的相关关系时,我们需要借助数据说话,即通过样本数据分析,从数据中提取信息,并构建适当的模型,再利用模型进行估计或判断.
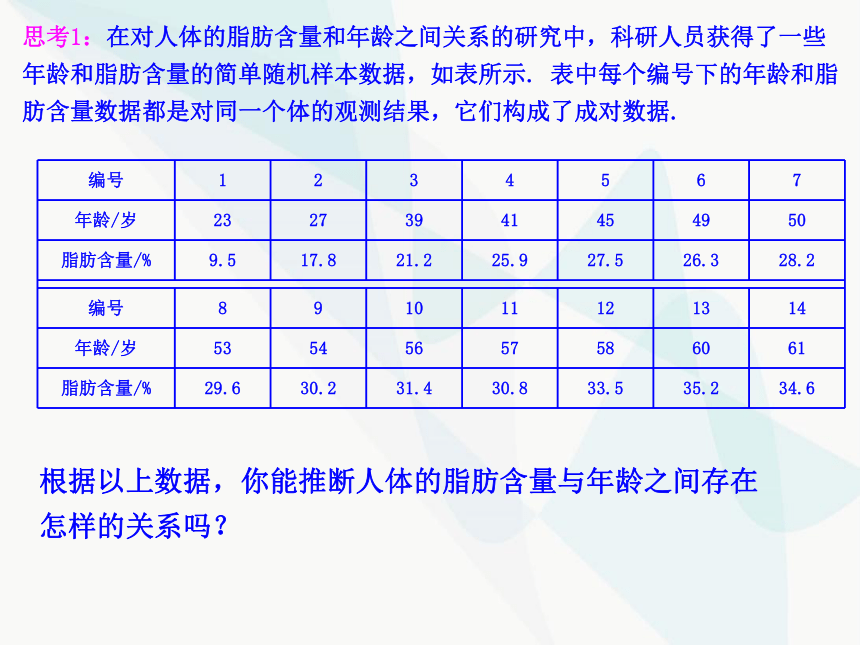
思考1:在对人体的脂肪含量和年龄之间关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机样本数据,如表所示. 表中每个编号下的年龄和脂肪含量数据都是对同一个体的观测结果,它们构成了成对数据.
编号 1 2 3 4 5 6 7
年龄/岁 23 27 39 41 45 49 50
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2
编号 8 9 10 11 12 13 14
年龄/岁 53 54 56 57 58 60 61
脂肪含量/% 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据以上数据,你能推断人体的脂肪含量与年龄之间存在怎样的关系吗?
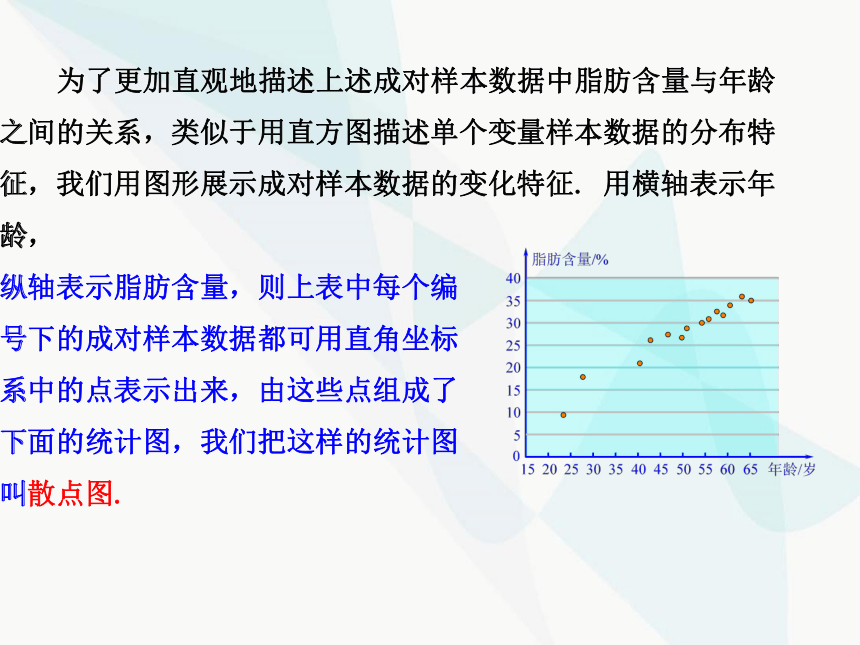
为了更加直观地描述上述成对样本数据中脂肪含量与年龄之间的关系,类似于用直方图描述单个变量样本数据的分布特征,我们用图形展示成对样本数据的变化特征. 用横轴表示年龄,
纵轴表示脂肪含量,则上表中每个编
号下的成对样本数据都可用直角坐标
系中的点表示出来,由这些点组成了
下面的统计图,我们把这样的统计图
叫散点图.
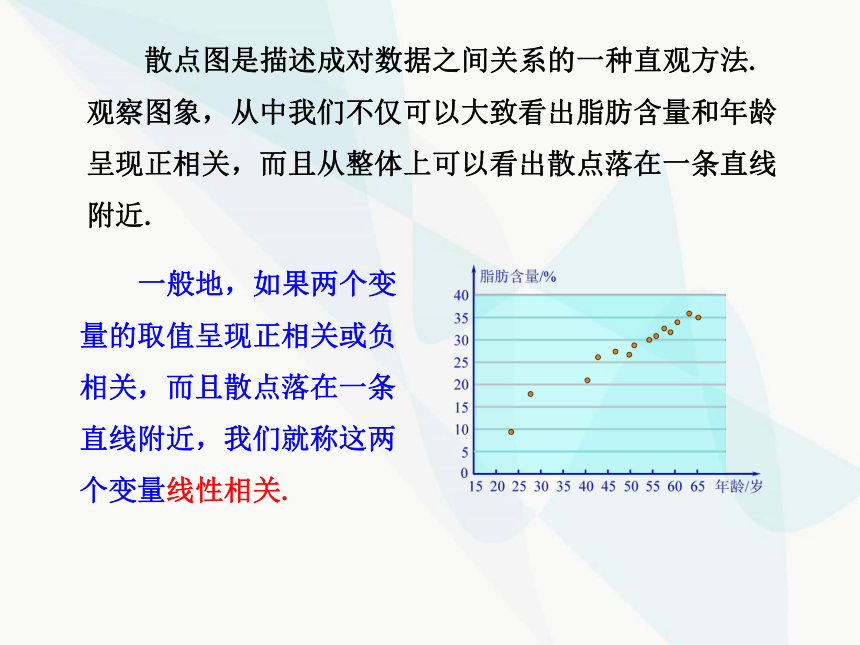
观察图象可以发现,这些散点大致落在一条从左下角到右上角的直线附近,表明随年龄的增加,相应的脂肪含量值呈现增加的趋势. 这样,由成对样本数据的分布规律,我们可以推断脂肪含量变量和年龄变量之间存在着相关关系.
从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,我们就称这两个变量正相关;当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关.
根据图象,能够推断脂肪含量与年龄这两个变量正相关.
散点图是描述成对数据之间关系的一种直观方法. 观察图象,从中我们不仅可以大致看出脂肪含量和年龄呈现正相关,而且从整体上可以看出散点落在一条直线附近.
一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们就称这两个变量线性相关.
观察下面的散点图,我们发现:
图(1)中的散点落在某条曲线附近,而不是落在一条直线附近,说明这两个变量具有相关性,但不是线性相关;
图(1)
图(2)
图(3)
类似地,图(2)中的散点落在一条折线附近,这两个变量也具有相关性,但它们既不是正相关,也不是负相关;图(3)中的散点杂乱无章,无规律可言,看不出这两个变量有什么相关性.
一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关.
例1.(多选)下列关系中,属于相关关系的是( )
A.正方形的边长与面积之间的关系
B.农作物的产量与施肥量之间的关系
C.出租车费与行驶的里程
D.降雪量与交通事故的发生率之间的关系
BD
变式:1.已知相关关系:①正相关,②负相关,③不相关.则图(1)(2)(3)分别反映的两变量间的相关关系是( )
A.①②③ B.②③① C.②①③ D.①③②
D
问题提出
2.1相关系数
如图7-7,易知这7组成对数据均位于单位圆上,所以X和Y不具备线性关系.
因此,为了使建立的线性回归方程有意义,在利用最小二乘法求线性回归方程之前,我们需要先对变量之间的线性关系作一个判断,如果数据不多,可以根据给定的数据画出散点图,再从直观上进行观测.但是对一般的情形又如何判断呢?
分析理解
抽象概括
显然,样本(线性)相关系数r的取值范围为[―1,1].
| r |值越接近1,随机变量之间的线性相关程度越强;| r |值越接近0,随机变量之间的线性相关程度越弱.
当r>0时,两个随机变量的值总体上变化趋势相同,此时称两个随机变量正相关;
当r<0时,两个随机变量的值总体上变化趋势相反,此时称两个随机变量负相关;
当r=0时,此时称两个随机变量线性不相关.
相关系数
r>0正相关;r<0负相关.通常,r>0.75,认为两个变量有很强的相关性.
本例中,由上面公式r=0.798>0.75.
*
*
如何描述两个变量之间线性相关关系的强弱?
我们学习了用相关系数r来衡量两个变量
之间线性相关关系的方法。
相关系数r
*
*
相关关系的测度
(相关系数取值及其意义)
-1.0
+1.0
0
-0.5
+0.5
完全负相关
无线性相关
完全正相关
负相关程度增加
r
正相关程度增加
*
*
1.思考辨析(正确的画“√”,错误的画“×”)
(1)散点图是判断两个变量是否相关的一种重要方法和手段.( )
(2)两个变量的相关系数越大,它们的相关程度越强.( )
(3)当一个变量的值增加时,另一个变量的值随之减少,则称这两个变量负相关.( )
(4)一般地,样本容量越大,用样本相关系数估计两个变量的相关系数的效果越好.( )
√
×
×
√
巩固提升
2.对变量 x,y,由观测数据得散点图(1);对变量 y,z,由观测数据得散点图(2).由这两个散点图可以判断( )
A.变量 x 与 y 正相关, x 与 z 正相关
B.变量 x 与 y 正相关, x 与 z 负相关
C.变量 x 与 y 负相关, x 与 z 正相关
D.变量 x 与 y 负相关, x 与 z 负相关
D
3.已知两个变量负相关,且相关程度很强,则它们的相关系数的大小可能是( )
A.-0.95 B.-0.13
C.0.15 D.0.96
解析:相关系数r<0时,成对数据负相关,且|r|越大,两个变量之间的线性相关程度越强.
答案:A
4.用线性回归模型求得甲、乙、丙3组不同的数据的线性相关系数分别为0.81,-0.98,0.63,其中________(填甲、乙、丙中的一个)组数据的线性相关性最强.
解析:|r|越接近1,两个变量的线性相关性越强,而|-0.98|>|0.81|>|0.63|,所以乙组数据的线性相关性最强.
答案:乙
例1 计算表7-1中随机变量之间的样本相关系数度(结果保留到小数点后的第9位),并谈谈通过计算发现了什么.
解(1)根据表7-1,得到表7-4.
例2 计算表7-5中两个随机变量之间的样本相关系数二并谈谈通过计算发现了什么.
解(1)根据表7-5中的数据,得到表7-6.表7-6
.
变式1: 为了对2020年某校期末成绩进行分析,在60分以上的全体同学中随机抽取8位,他们的数学、物理成绩对应如下表:
学生编号 1 2 3 4 5 6 7 8
数学成绩x 68 72 78 81 85 88 91 93
物理成绩y 70 66 81 83 79 80 92 89
变式2:在一段时间内,某中商品的价格x元和需求量Y件之间的一组数据为:
求出Y对的回归直线方程,并说明拟合效果的好坏。
价格x 14 16 18 20 22
需求量Y 12 10 7 5 3
解:
变式2:在一段时间内,某中商品的价格x元和需求量Y件之间的一组数据为:
求出Y对的回归直线方程,并说明拟合效果的好坏。
价格x 14 16 18 20 22
需求量Y 12 10 7 5 3
列出残差表为
0.994
因而,拟合效果较好。
0
0.3
-0.4
-0.1
0.2
4.6
2.6
-0.4
-2.4
-4.4
我们知道,一名学生学习中的不同学科成绩有着密不可分的关系,但它们之间的相关性如何呢?与我们的普遍认识之间是否存在差异呢?下面以化学成绩和物理成绩为例加以说明.
例3 表7-7中是在某校高二年级中抽取了246名学生的化学成绩(单位:分)和物理成绩(单位:分),求这组成对数据中化学成绩和物理成绩的样本相关系数.
解 鉴于学生人数较多,手动计算样本相关系数工作量较大,这里借助Excel软件进行 分析(注意:分析时,需要将数据进行整理,排成3列,246行).
(1)画出它们的散点图,如图7-10.
(2)求出样本相关系数r=0.397.
这个结果说明该校高二年级学生的化学成绩和物理成绩之间的线性相关性比较弱.
案例 一只红铃虫的产卵数y和温度x有关。现收集了7组观测数据列于表中:
(1)试建立产卵数y与温度x之间的回归方程;并预测温度为28oC时产卵数目。
(2)你所建立的模型中温度在多大程度上解释了产卵数的变化?
温度xoC
21
23
25
27
29
32
35
产卵数y/个
7
11
21
24
66
115
325
非线性回归问题
补充提升
选 模 型
由计算器得:线性回归方程为y=19.87x-463.73
相关指数R2=r2≈0.8642=0.7464
估计参数
解:选取气温为解释变量x,产卵数
为预报变量y。
选变量
所以,一次函数模型中温度解释了74.64%的产卵数变化。
探索新知
画散点图
0
50
100
150
200
250
300
350
0
3
6
9
12
15
18
21
24
27
30
33
36
39
方案1
分析和预测
当x=28时,y =19.87×28-463.73≈ 93
一元线性模型
假设线性回归方程为 :
奇怪?
93>66
模型不好?
y=bx2+a 变换 y=bt+a
非线性关系 线性关系
方案2
问题1
选用y=bx2+a ,还是y=bx2+cx+a ?
问题3
产卵数
气温
问题2
如何求a、b ?
合作探究
t=x2
二次函数模型
方案2解答
平方变换:令t=x2,产卵数y和温度x之间二次函数模型y=bx2+a就转化为产卵数y和温度的平方t之间线性回归模型y=bt+a
温度
21
23
25
27
29
32
35
温度的平方t
441
529
625
729
841
1024
1225
产卵数y/个
7
11
21
24
66
115
325
作散点图,并由计算器得:y和t之间的线性回归方程为y=0.367t-202.543,相关指数R2=0.802
将t=x2代入线性回归方程得:
y=0.367x2 -202.543
当x=28时,y=0.367×282-202.54≈85,且R2=0.802,
所以,二次函数模型中温度解
释了80.2%的产卵数变化。
t
问题2
变换 y=bx+a
非线性关系 线性关系
问题1
如何选取指数函数的底
产卵数
气温
指数函数模型
方案3
合作探究
对数
方案3解答
温度xoC
21
23
25
27
29
32
35
z=lny
1.946
2.398
3.045
3.178
4.190
4.745
5.784
产卵数y/个
7
11
21
24
66
115
325
x
z
当x=28oC 时,y ≈44 ,指数回归模型中温度解释了98.5%的产卵数的变化
由计算器得:z关于x的线性回归方程
为
对数变换:在 中两边取常用对数得
令 ,则
就转换为z=bx+a.
相关指数R2=0.98
最好的模型是哪个
产卵数
气温
产卵数
气温
线性模型
二次函数模型
指数函数模型
比一比
函数模型 相关指数R2
线性回归模型 0.7464
二次函数模型 0.80
指数函数模型 0.98
最好的模型是哪个
回归分析(二)
则回归方程的残差计算公式分别为:
由计算可得:
x 21 23 25 27 29 32 35
y 7 11 21 24 66 115 325
0.557 -0.101 1.875 -8.950 9.230 -13.381 34.675
47.696 19.400 -5.832 -41.00 -40.104 -58.265 77.968
因此模型(1)的拟合效果远远优于模型(2)。
变式. 某出版社单册图书的成本费y(元)与印刷册数x(千册)有关,经统计得到数据如下:
x 1 2 3 5 7 10 11 20 25 30
y 9.02 5.27 4.06 3.03 2.59 2.28 2.21 1.89 1.80 1.75
例4. 某出版社单册图书的成本费y(元)与印刷册数x(千册)有关,经统计得到数据如下:
x 1 2 3 5 7 10 11 20 25 30
y 9.02 5.27 4.06 3.03 2.59 2.28 2.21 1.89 1.80 1.75
x 1 2 3 5 7 10 11 20 25 30
t 1 0.5 0.333 0.2 0.143 0.1 0.091 0.05 0.04 0.033
y 9.02 5.27 4.06 3.03 2.59 2.28 2.21 1.89 1.80 1.75
1.(多选)在下列各图中,两个变量具有相关关系的是( )
BC
课堂练习
AC
A
X 5 10 15 20 25
Y 103 105 110 111 114
4.如图所示,给出了样本量均为7的 A,B 两组样本数据的散点图,已知 A组样本数据的相关系数为 r1,B 组数据的相关系数为 r2,则有r1________r2(填“>”或“<”号).
>
D
21 23 25 27 29 32 35
7 11 21 24 66 115 325
1.成对数据的相关关系
2.散点图
3.相关关系的分类
正相关和负相关
线性相关和非线性相关
小结
4. 样本相关系数r
(1)当r >0时,称成对数据正相关;当r <0时,称成对数据负相关.
(2)r 的取值范围为[-1,1]
(3)当|r|越接近1时,成对样本数据的线性相关程度越强;当|r|越接近0时,成对样本数据的线性相关程度越弱.
7.2成对数据的线性相关性
1、所求直线方程叫做回归直线方程;
相应的直线叫做回归直线。
2、对两个变量进行的线性分析叫做线性回归分析。
回归直线方程
温故知新
最小二乘法:
称为样本点的中心。
www.
温故知新
2、求回归直线方程的步骤:
(3)代入公式
(4)写出直线方程为y=bx+a,即为所求的回归直线方程。
^
温故知新
我们知道,如果变量 y 是变量 x 的函数,那么由 x 就可以唯一确定 y. 然而,现实世界中还存在这样的情况:两个变量之间有关系,但密切程度又达不到函数关系的程度. 例如,人的体重与身高存在关系,但由一个人的身高并不能确定他的体重值. 那么,该如何刻画这两个变量之间的关系呢?下面我们就来研究这个问题.
引入新课
我们知道,一个人的体重与他的身高有关系. 一般而言,个子高的人往往体重值较大,个子矮的人往往体重值较小. 但身高并不是决定体重的唯一因素,例如生活中的饮食习惯、体育锻炼、睡眠时间以及遗传因素等也是影响体重的重要因素. 像这样,两个变量有关系,但又没有确切到可由其中一个去精确地决定另一个的程度,这种关系称为相关关系.
变量的相关关系
两个变量具有相关关系的事例在现实中大量存在. 例如:
1.子女身高 y 与父亲身高 x 之间的关系;
2.商品销售收入 y 与广告支出 x 之间的关系;
3.空气污染指数 y 与汽车保有量 x 之间的关系;
4.粮食亩产量 y 与施肥量 x 之间的关系.
对上述各例中两个变量之间的相关关系,我们往往会根据自己以往积累的经验作出推断. “经验之中有规律”,经验的确可以为我们的决策提供一定的依据,但仅凭经验推断又有不足.
因为在相关关系中,变量 y 的值不能随变量 x 的值的确定而唯一确定,所以我们无法直接用函数去描述变量之间的这种关系. 因此,在研究两个变量之间的相关关系时,我们需要借助数据说话,即通过样本数据分析,从数据中提取信息,并构建适当的模型,再利用模型进行估计或判断.
思考1:在对人体的脂肪含量和年龄之间关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机样本数据,如表所示. 表中每个编号下的年龄和脂肪含量数据都是对同一个体的观测结果,它们构成了成对数据.
编号 1 2 3 4 5 6 7
年龄/岁 23 27 39 41 45 49 50
脂肪含量/% 9.5 17.8 21.2 25.9 27.5 26.3 28.2
编号 8 9 10 11 12 13 14
年龄/岁 53 54 56 57 58 60 61
脂肪含量/% 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据以上数据,你能推断人体的脂肪含量与年龄之间存在怎样的关系吗?
为了更加直观地描述上述成对样本数据中脂肪含量与年龄之间的关系,类似于用直方图描述单个变量样本数据的分布特征,我们用图形展示成对样本数据的变化特征. 用横轴表示年龄,
纵轴表示脂肪含量,则上表中每个编
号下的成对样本数据都可用直角坐标
系中的点表示出来,由这些点组成了
下面的统计图,我们把这样的统计图
叫散点图.
观察图象可以发现,这些散点大致落在一条从左下角到右上角的直线附近,表明随年龄的增加,相应的脂肪含量值呈现增加的趋势. 这样,由成对样本数据的分布规律,我们可以推断脂肪含量变量和年龄变量之间存在着相关关系.
从整体上看,当一个变量的值增加时,另一个变量的相应值也呈现增加的趋势,我们就称这两个变量正相关;当一个变量的值增加时,另一个变量的相应值呈现减少的趋势,则称这两个变量负相关.
根据图象,能够推断脂肪含量与年龄这两个变量正相关.
散点图是描述成对数据之间关系的一种直观方法. 观察图象,从中我们不仅可以大致看出脂肪含量和年龄呈现正相关,而且从整体上可以看出散点落在一条直线附近.
一般地,如果两个变量的取值呈现正相关或负相关,而且散点落在一条直线附近,我们就称这两个变量线性相关.
观察下面的散点图,我们发现:
图(1)中的散点落在某条曲线附近,而不是落在一条直线附近,说明这两个变量具有相关性,但不是线性相关;
图(1)
图(2)
图(3)
类似地,图(2)中的散点落在一条折线附近,这两个变量也具有相关性,但它们既不是正相关,也不是负相关;图(3)中的散点杂乱无章,无规律可言,看不出这两个变量有什么相关性.
一般地,如果两个变量具有相关性,但不是线性相关,那么我们就称这两个变量非线性相关或曲线相关.
例1.(多选)下列关系中,属于相关关系的是( )
A.正方形的边长与面积之间的关系
B.农作物的产量与施肥量之间的关系
C.出租车费与行驶的里程
D.降雪量与交通事故的发生率之间的关系
BD
变式:1.已知相关关系:①正相关,②负相关,③不相关.则图(1)(2)(3)分别反映的两变量间的相关关系是( )
A.①②③ B.②③① C.②①③ D.①③②
D
问题提出
2.1相关系数
如图7-7,易知这7组成对数据均位于单位圆上,所以X和Y不具备线性关系.
因此,为了使建立的线性回归方程有意义,在利用最小二乘法求线性回归方程之前,我们需要先对变量之间的线性关系作一个判断,如果数据不多,可以根据给定的数据画出散点图,再从直观上进行观测.但是对一般的情形又如何判断呢?
分析理解
抽象概括
显然,样本(线性)相关系数r的取值范围为[―1,1].
| r |值越接近1,随机变量之间的线性相关程度越强;| r |值越接近0,随机变量之间的线性相关程度越弱.
当r>0时,两个随机变量的值总体上变化趋势相同,此时称两个随机变量正相关;
当r<0时,两个随机变量的值总体上变化趋势相反,此时称两个随机变量负相关;
当r=0时,此时称两个随机变量线性不相关.
相关系数
r>0正相关;r<0负相关.通常,r>0.75,认为两个变量有很强的相关性.
本例中,由上面公式r=0.798>0.75.
*
*
如何描述两个变量之间线性相关关系的强弱?
我们学习了用相关系数r来衡量两个变量
之间线性相关关系的方法。
相关系数r
*
*
相关关系的测度
(相关系数取值及其意义)
-1.0
+1.0
0
-0.5
+0.5
完全负相关
无线性相关
完全正相关
负相关程度增加
r
正相关程度增加
*
*
1.思考辨析(正确的画“√”,错误的画“×”)
(1)散点图是判断两个变量是否相关的一种重要方法和手段.( )
(2)两个变量的相关系数越大,它们的相关程度越强.( )
(3)当一个变量的值增加时,另一个变量的值随之减少,则称这两个变量负相关.( )
(4)一般地,样本容量越大,用样本相关系数估计两个变量的相关系数的效果越好.( )
√
×
×
√
巩固提升
2.对变量 x,y,由观测数据得散点图(1);对变量 y,z,由观测数据得散点图(2).由这两个散点图可以判断( )
A.变量 x 与 y 正相关, x 与 z 正相关
B.变量 x 与 y 正相关, x 与 z 负相关
C.变量 x 与 y 负相关, x 与 z 正相关
D.变量 x 与 y 负相关, x 与 z 负相关
D
3.已知两个变量负相关,且相关程度很强,则它们的相关系数的大小可能是( )
A.-0.95 B.-0.13
C.0.15 D.0.96
解析:相关系数r<0时,成对数据负相关,且|r|越大,两个变量之间的线性相关程度越强.
答案:A
4.用线性回归模型求得甲、乙、丙3组不同的数据的线性相关系数分别为0.81,-0.98,0.63,其中________(填甲、乙、丙中的一个)组数据的线性相关性最强.
解析:|r|越接近1,两个变量的线性相关性越强,而|-0.98|>|0.81|>|0.63|,所以乙组数据的线性相关性最强.
答案:乙
例1 计算表7-1中随机变量之间的样本相关系数度(结果保留到小数点后的第9位),并谈谈通过计算发现了什么.
解(1)根据表7-1,得到表7-4.
例2 计算表7-5中两个随机变量之间的样本相关系数二并谈谈通过计算发现了什么.
解(1)根据表7-5中的数据,得到表7-6.表7-6
.
变式1: 为了对2020年某校期末成绩进行分析,在60分以上的全体同学中随机抽取8位,他们的数学、物理成绩对应如下表:
学生编号 1 2 3 4 5 6 7 8
数学成绩x 68 72 78 81 85 88 91 93
物理成绩y 70 66 81 83 79 80 92 89
变式2:在一段时间内,某中商品的价格x元和需求量Y件之间的一组数据为:
求出Y对的回归直线方程,并说明拟合效果的好坏。
价格x 14 16 18 20 22
需求量Y 12 10 7 5 3
解:
变式2:在一段时间内,某中商品的价格x元和需求量Y件之间的一组数据为:
求出Y对的回归直线方程,并说明拟合效果的好坏。
价格x 14 16 18 20 22
需求量Y 12 10 7 5 3
列出残差表为
0.994
因而,拟合效果较好。
0
0.3
-0.4
-0.1
0.2
4.6
2.6
-0.4
-2.4
-4.4
我们知道,一名学生学习中的不同学科成绩有着密不可分的关系,但它们之间的相关性如何呢?与我们的普遍认识之间是否存在差异呢?下面以化学成绩和物理成绩为例加以说明.
例3 表7-7中是在某校高二年级中抽取了246名学生的化学成绩(单位:分)和物理成绩(单位:分),求这组成对数据中化学成绩和物理成绩的样本相关系数.
解 鉴于学生人数较多,手动计算样本相关系数工作量较大,这里借助Excel软件进行 分析(注意:分析时,需要将数据进行整理,排成3列,246行).
(1)画出它们的散点图,如图7-10.
(2)求出样本相关系数r=0.397.
这个结果说明该校高二年级学生的化学成绩和物理成绩之间的线性相关性比较弱.
案例 一只红铃虫的产卵数y和温度x有关。现收集了7组观测数据列于表中:
(1)试建立产卵数y与温度x之间的回归方程;并预测温度为28oC时产卵数目。
(2)你所建立的模型中温度在多大程度上解释了产卵数的变化?
温度xoC
21
23
25
27
29
32
35
产卵数y/个
7
11
21
24
66
115
325
非线性回归问题
补充提升
选 模 型
由计算器得:线性回归方程为y=19.87x-463.73
相关指数R2=r2≈0.8642=0.7464
估计参数
解:选取气温为解释变量x,产卵数
为预报变量y。
选变量
所以,一次函数模型中温度解释了74.64%的产卵数变化。
探索新知
画散点图
0
50
100
150
200
250
300
350
0
3
6
9
12
15
18
21
24
27
30
33
36
39
方案1
分析和预测
当x=28时,y =19.87×28-463.73≈ 93
一元线性模型
假设线性回归方程为 :
奇怪?
93>66
模型不好?
y=bx2+a 变换 y=bt+a
非线性关系 线性关系
方案2
问题1
选用y=bx2+a ,还是y=bx2+cx+a ?
问题3
产卵数
气温
问题2
如何求a、b ?
合作探究
t=x2
二次函数模型
方案2解答
平方变换:令t=x2,产卵数y和温度x之间二次函数模型y=bx2+a就转化为产卵数y和温度的平方t之间线性回归模型y=bt+a
温度
21
23
25
27
29
32
35
温度的平方t
441
529
625
729
841
1024
1225
产卵数y/个
7
11
21
24
66
115
325
作散点图,并由计算器得:y和t之间的线性回归方程为y=0.367t-202.543,相关指数R2=0.802
将t=x2代入线性回归方程得:
y=0.367x2 -202.543
当x=28时,y=0.367×282-202.54≈85,且R2=0.802,
所以,二次函数模型中温度解
释了80.2%的产卵数变化。
t
问题2
变换 y=bx+a
非线性关系 线性关系
问题1
如何选取指数函数的底
产卵数
气温
指数函数模型
方案3
合作探究
对数
方案3解答
温度xoC
21
23
25
27
29
32
35
z=lny
1.946
2.398
3.045
3.178
4.190
4.745
5.784
产卵数y/个
7
11
21
24
66
115
325
x
z
当x=28oC 时,y ≈44 ,指数回归模型中温度解释了98.5%的产卵数的变化
由计算器得:z关于x的线性回归方程
为
对数变换:在 中两边取常用对数得
令 ,则
就转换为z=bx+a.
相关指数R2=0.98
最好的模型是哪个
产卵数
气温
产卵数
气温
线性模型
二次函数模型
指数函数模型
比一比
函数模型 相关指数R2
线性回归模型 0.7464
二次函数模型 0.80
指数函数模型 0.98
最好的模型是哪个
回归分析(二)
则回归方程的残差计算公式分别为:
由计算可得:
x 21 23 25 27 29 32 35
y 7 11 21 24 66 115 325
0.557 -0.101 1.875 -8.950 9.230 -13.381 34.675
47.696 19.400 -5.832 -41.00 -40.104 -58.265 77.968
因此模型(1)的拟合效果远远优于模型(2)。
变式. 某出版社单册图书的成本费y(元)与印刷册数x(千册)有关,经统计得到数据如下:
x 1 2 3 5 7 10 11 20 25 30
y 9.02 5.27 4.06 3.03 2.59 2.28 2.21 1.89 1.80 1.75
例4. 某出版社单册图书的成本费y(元)与印刷册数x(千册)有关,经统计得到数据如下:
x 1 2 3 5 7 10 11 20 25 30
y 9.02 5.27 4.06 3.03 2.59 2.28 2.21 1.89 1.80 1.75
x 1 2 3 5 7 10 11 20 25 30
t 1 0.5 0.333 0.2 0.143 0.1 0.091 0.05 0.04 0.033
y 9.02 5.27 4.06 3.03 2.59 2.28 2.21 1.89 1.80 1.75
1.(多选)在下列各图中,两个变量具有相关关系的是( )
BC
课堂练习
AC
A
X 5 10 15 20 25
Y 103 105 110 111 114
4.如图所示,给出了样本量均为7的 A,B 两组样本数据的散点图,已知 A组样本数据的相关系数为 r1,B 组数据的相关系数为 r2,则有r1________r2(填“>”或“<”号).
>
D
21 23 25 27 29 32 35
7 11 21 24 66 115 325
1.成对数据的相关关系
2.散点图
3.相关关系的分类
正相关和负相关
线性相关和非线性相关
小结
4. 样本相关系数r
(1)当r >0时,称成对数据正相关;当r <0时,称成对数据负相关.
(2)r 的取值范围为[-1,1]
(3)当|r|越接近1时,成对样本数据的线性相关程度越强;当|r|越接近0时,成对样本数据的线性相关程度越弱.
同课章节目录
