北师大版高中数学选择性必修第一册 3.2.1从平面向量到空间向量、空间向量的运算 课件(共21张PPT)
文档属性
| 名称 | 北师大版高中数学选择性必修第一册 3.2.1从平面向量到空间向量、空间向量的运算 课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1020.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 11:04:07 | ||
图片预览







文档简介
(共21张PPT)
3.2.1
从平面向量到空间向量、空间向量的运算(加减法与数乘)
北师大版选择性必修一
复面向量的有关概念
定义:
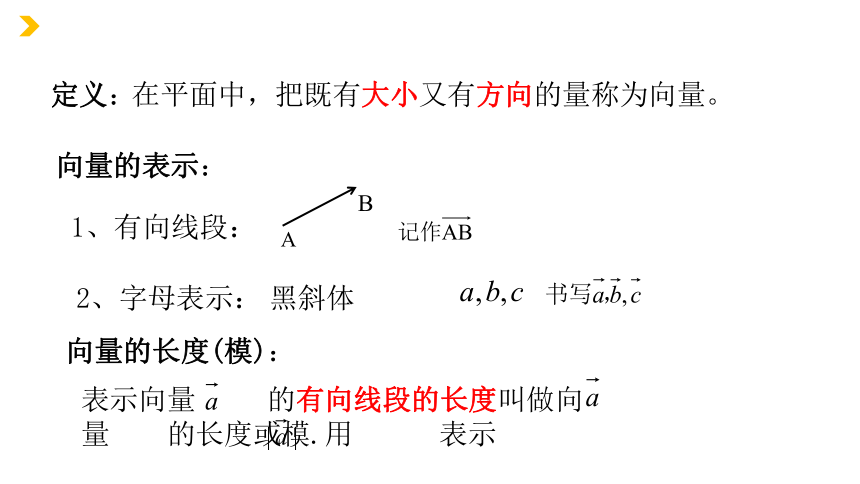
在平面中,把既有大小又有方向的量称为向量。
向量的表示:
1、有向线段:
2、字母表示:
向量的长度(模):
黑斜体
表示向量 的有向线段的长度叫做向量 的长度或模.用 表示
复面向量的有关概念
两个常见向量
单位向量
零向量
长度为1的向量
长度为0的向量
向量的基本关系
相等向量
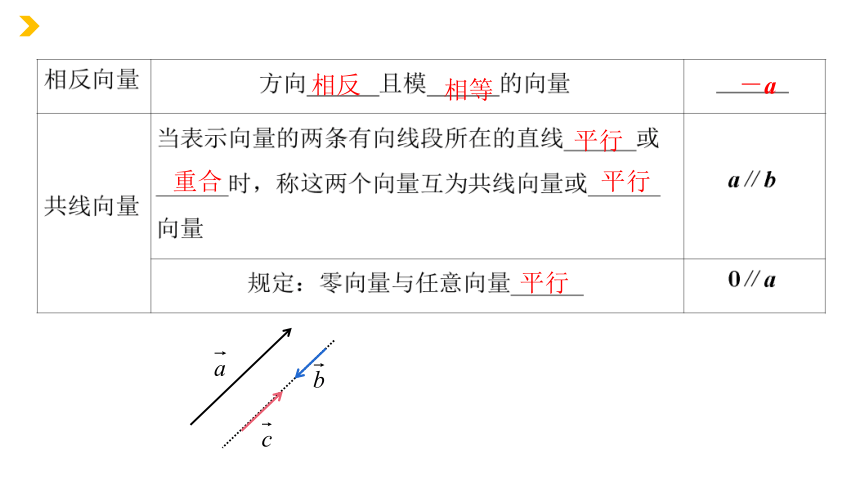
共线向量
相反向量
空间向量的有关概念
思考 我们应该如何定义空间中的向量呢?
定义:
在空间中,我们把具有大小和方向的量称为空间向量。
空间向量的表示:
1、有向线段:
2、字母表示:
起点
终点
黑斜体
空间向量的有关概念
思考 通过比较平面向量与空间向量的定义,你有什么发现?
思考 由平面向量到空间向量的定义用到了什么方法?用此方法你能否定义空间向量的其他相关概念?
平面向量与空间向量只是研究的范围不同.平面向量扩展到空间就是空间向量。
类比的方法
空间向量的模:
表示向量 的有向线段的长度叫做向量 的长度或模.用 表示
空间向量的有关概念
0
1
1
相同
1
相等
空间向量的有关概念
相反
相等
-a
平行
重合
平行
平行
空间向量的有关概念
平行于
在
共面
空间向量的有关概念
空间向量的有关概念
空间向量的有关概念
相同
相反
空间向量的加减法与数乘运算
空间向量的加减法与数乘运算
向量共线问题
共线向量基本定理(一维向量基本定理):空间两个向量a,b(b≠0)共线的充要条件是存在唯一的实数λ,使____________.
a=λb
向量共线问题
向量共线问题
空间向量共面问题
共面向量的充要条件:若两个向量a,b不共线,则向量c与向量a,b共面的充要条件是存在唯一的有序实数对(x,y),使c=_______________.
xa+yb
空间向量共面问题
空间向量共面问题
空间向量共面问题
课堂小结
1.知识清单:
(1)向量的相关概念.(2)向量的线性运算(加法、减法和数乘).(3)向量的线性运算的运算律.
(4)共线向量基本定理.(5)空间向量共面的充要条件.
2.方法归纳:
三角形法则、平行四边形法则、数形结合思想、转化化归思想.
3.常见误区:
(1)对空间向量的理解应抓住向量的“大小”和“方向”两个要素,并注意它是一个“量”,而不是一个数.
(2)混淆向量共线与线段共线、点共线.
3.2.1
从平面向量到空间向量、空间向量的运算(加减法与数乘)
北师大版选择性必修一
复面向量的有关概念
定义:
在平面中,把既有大小又有方向的量称为向量。
向量的表示:
1、有向线段:
2、字母表示:
向量的长度(模):
黑斜体
表示向量 的有向线段的长度叫做向量 的长度或模.用 表示
复面向量的有关概念
两个常见向量
单位向量
零向量
长度为1的向量
长度为0的向量
向量的基本关系
相等向量
共线向量
相反向量
空间向量的有关概念
思考 我们应该如何定义空间中的向量呢?
定义:
在空间中,我们把具有大小和方向的量称为空间向量。
空间向量的表示:
1、有向线段:
2、字母表示:
起点
终点
黑斜体
空间向量的有关概念
思考 通过比较平面向量与空间向量的定义,你有什么发现?
思考 由平面向量到空间向量的定义用到了什么方法?用此方法你能否定义空间向量的其他相关概念?
平面向量与空间向量只是研究的范围不同.平面向量扩展到空间就是空间向量。
类比的方法
空间向量的模:
表示向量 的有向线段的长度叫做向量 的长度或模.用 表示
空间向量的有关概念
0
1
1
相同
1
相等
空间向量的有关概念
相反
相等
-a
平行
重合
平行
平行
空间向量的有关概念
平行于
在
共面
空间向量的有关概念
空间向量的有关概念
空间向量的有关概念
相同
相反
空间向量的加减法与数乘运算
空间向量的加减法与数乘运算
向量共线问题
共线向量基本定理(一维向量基本定理):空间两个向量a,b(b≠0)共线的充要条件是存在唯一的实数λ,使____________.
a=λb
向量共线问题
向量共线问题
空间向量共面问题
共面向量的充要条件:若两个向量a,b不共线,则向量c与向量a,b共面的充要条件是存在唯一的有序实数对(x,y),使c=_______________.
xa+yb
空间向量共面问题
空间向量共面问题
空间向量共面问题
课堂小结
1.知识清单:
(1)向量的相关概念.(2)向量的线性运算(加法、减法和数乘).(3)向量的线性运算的运算律.
(4)共线向量基本定理.(5)空间向量共面的充要条件.
2.方法归纳:
三角形法则、平行四边形法则、数形结合思想、转化化归思想.
3.常见误区:
(1)对空间向量的理解应抓住向量的“大小”和“方向”两个要素,并注意它是一个“量”,而不是一个数.
(2)混淆向量共线与线段共线、点共线.
同课章节目录
