北师大版高中数学选择性必修第一册 3.3.2第2课时空间向量运算的坐标表示及应用 课件(共15张PPT)
文档属性
| 名称 | 北师大版高中数学选择性必修第一册 3.3.2第2课时空间向量运算的坐标表示及应用 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 418.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 11:05:48 | ||
图片预览




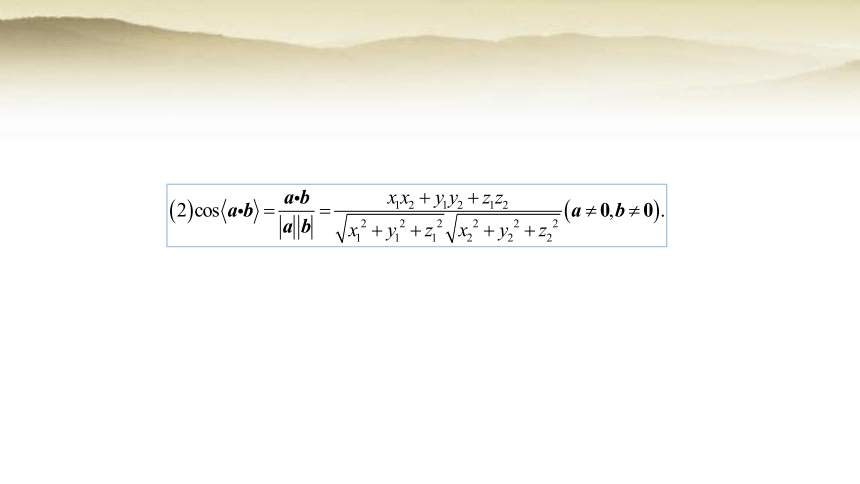


文档简介
(共15张PPT)
3.3.2 第2课时
新授课
空间向量运算的坐标表示及应用
1.进一步熟悉空间向量的坐标表示.
2.能利用空间向量的坐标解决一些简单的长度与夹角问题.
复习回顾:空间向量运算的坐标表示有哪些?
设向量a=(x1,y1,z1),b=(x2,y2,z2),则
知识点:空间向量的长度与夹角的坐标表示
设向量a=(x1,y1,z1),b=(x2,y2,z2),根据空间向量运算的坐标表示,可以得到:
若点A的坐标为(a1,b1,c1),点B的坐标为(a2,b2,c2),
则
例1:已知空间三点A(1,0,0),B(3,1,1),C(2,0,1),求线段AB的长和∠BAC的大小.
解:
又∵两个向量的夹角取值范围为[0,π],
归纳总结
1.求空间中线段的长度即对应空间向量的模,因此空间两点间的距离公式就是空间向量模的计算.
2.(1)〈a,b〉∈[0,π].
(2)空间两直线夹角可转化为两向量的夹角,设直线AB与CD所成的角为θ,则
练一练
1.已知A(1,0,1),B(1,1,1),C(2,3,2),D(0,2,3),写出向量
的坐标,并求出它们的长度.
2.已知空间向量a=(0,1,1),b=(-1,0,1),则a与b的夹角为 .
解:∵空间向量a=(0,1,1),b=(-1,0,1),
∴a与b的夹角θ满足
例2:如图,三棱柱ABC-A'B'C'中,侧棱与底面垂直,CA=CB=1,∠BCA=
棱AA'=2,点M,N分别是A'B'和A'A的中点.
(1)求 ;(2)求 的值;(3)求证:
解:如图,以点C为原点,CA,CB,CC'所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
(1)由题意,得B(0,1,0),N(1,0,1).
则
例2:如图,三棱柱ABC-A'B'C'中,侧棱与底面垂直,CA=CB=1,∠BCA=
棱AA'=2,点M,N分别是A'B'和A'A的中点.
(1)求 ;(2)求 的值;(3)求证:
(2)由题意,得B(0,1,0),C(0,0,0),A'(1,0,2),B'(0,1,2).
例2:如图,三棱柱ABC-A'B'C'中,侧棱与底面垂直,CA=CB=1,∠BCA=
棱AA'=2,点M,N分别是A'B'和A'A的中点.
(1)求 ;(2)求 的值;(3)求证:
(3)由题意,得A'(1,0,2),B(0,1,0),C'(0,0,2),
归纳总结
空间向量的坐标运算的一般步骤
(1)建系:根据题目中的几何图形建立恰当的空间直角坐标系.
(2)求坐标:①求出相关点的坐标;②写出向量的坐标.
(3)论证、计算:结合公式进行论证、计算.
(4)转化:转化为平行与垂直、夹角与距离问题.
练一练
3.在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别是DD1,BD,BB1的中点.
(1)求证:EF⊥CF;(2)求EF与CG所成角的余弦值.
解:以点D为原点,以 为x,y,z轴的正方向,建立如图所示的空间直角坐标系D-xyz,
则
根据今天所学,回答下列问题:
1.如何根据空间向量坐标求长度及夹角?解题时需要注意什么?
2.空间向量的坐标运算的一般步骤有哪些?
3.3.2 第2课时
新授课
空间向量运算的坐标表示及应用
1.进一步熟悉空间向量的坐标表示.
2.能利用空间向量的坐标解决一些简单的长度与夹角问题.
复习回顾:空间向量运算的坐标表示有哪些?
设向量a=(x1,y1,z1),b=(x2,y2,z2),则
知识点:空间向量的长度与夹角的坐标表示
设向量a=(x1,y1,z1),b=(x2,y2,z2),根据空间向量运算的坐标表示,可以得到:
若点A的坐标为(a1,b1,c1),点B的坐标为(a2,b2,c2),
则
例1:已知空间三点A(1,0,0),B(3,1,1),C(2,0,1),求线段AB的长和∠BAC的大小.
解:
又∵两个向量的夹角取值范围为[0,π],
归纳总结
1.求空间中线段的长度即对应空间向量的模,因此空间两点间的距离公式就是空间向量模的计算.
2.(1)〈a,b〉∈[0,π].
(2)空间两直线夹角可转化为两向量的夹角,设直线AB与CD所成的角为θ,则
练一练
1.已知A(1,0,1),B(1,1,1),C(2,3,2),D(0,2,3),写出向量
的坐标,并求出它们的长度.
2.已知空间向量a=(0,1,1),b=(-1,0,1),则a与b的夹角为 .
解:∵空间向量a=(0,1,1),b=(-1,0,1),
∴a与b的夹角θ满足
例2:如图,三棱柱ABC-A'B'C'中,侧棱与底面垂直,CA=CB=1,∠BCA=
棱AA'=2,点M,N分别是A'B'和A'A的中点.
(1)求 ;(2)求 的值;(3)求证:
解:如图,以点C为原点,CA,CB,CC'所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
(1)由题意,得B(0,1,0),N(1,0,1).
则
例2:如图,三棱柱ABC-A'B'C'中,侧棱与底面垂直,CA=CB=1,∠BCA=
棱AA'=2,点M,N分别是A'B'和A'A的中点.
(1)求 ;(2)求 的值;(3)求证:
(2)由题意,得B(0,1,0),C(0,0,0),A'(1,0,2),B'(0,1,2).
例2:如图,三棱柱ABC-A'B'C'中,侧棱与底面垂直,CA=CB=1,∠BCA=
棱AA'=2,点M,N分别是A'B'和A'A的中点.
(1)求 ;(2)求 的值;(3)求证:
(3)由题意,得A'(1,0,2),B(0,1,0),C'(0,0,2),
归纳总结
空间向量的坐标运算的一般步骤
(1)建系:根据题目中的几何图形建立恰当的空间直角坐标系.
(2)求坐标:①求出相关点的坐标;②写出向量的坐标.
(3)论证、计算:结合公式进行论证、计算.
(4)转化:转化为平行与垂直、夹角与距离问题.
练一练
3.在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别是DD1,BD,BB1的中点.
(1)求证:EF⊥CF;(2)求EF与CG所成角的余弦值.
解:以点D为原点,以 为x,y,z轴的正方向,建立如图所示的空间直角坐标系D-xyz,
则
根据今天所学,回答下列问题:
1.如何根据空间向量坐标求长度及夹角?解题时需要注意什么?
2.空间向量的坐标运算的一般步骤有哪些?
同课章节目录
