北师大版高中数学选择性必修第一册 3.4.2第2课时用向量方法研究立体几何中的位置关系 课件(共13张PPT)
文档属性
| 名称 | 北师大版高中数学选择性必修第一册 3.4.2第2课时用向量方法研究立体几何中的位置关系 课件(共13张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 428.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 00:00:00 | ||
图片预览




文档简介
(共13张PPT)
3.4.2 第2课时
新授课
用向量方法研究立体几何中的位置关系
1.理解并掌握三垂线定理及其逆定理.
2.会用空间向量解决立体几何问题,掌握其一般步骤.
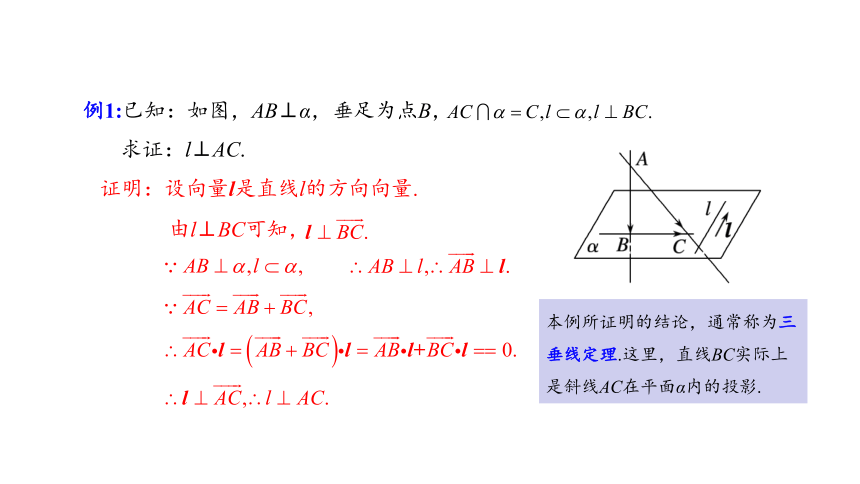
例1:已知:如图,AB⊥α,垂足为点B,
求证:l⊥AC.
证明:设向量l是直线l的方向向量.
由l⊥BC可知,
本例所证明的结论,通常称为三垂线定理.这里,直线BC实际上是斜线AC在平面α内的投影.
归纳总结
三垂线定理:若平面内的一条直线与平面的一条斜线在这个平面内的投影垂直,则它也和这条斜线垂直.
类似地可以得到:
三垂线定理的逆定理:若平面内的一条直线和这个平面的一条斜线垂直,则它也和这条斜线在这个平面内的投影垂直.
练一练
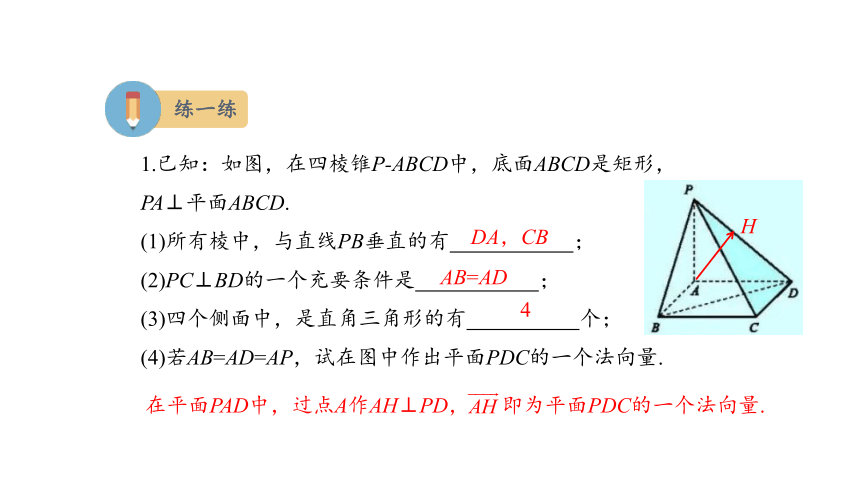
1.已知:如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD.
(1)所有棱中,与直线PB垂直的有 ;
(2)PC⊥BD的一个充要条件是 ;
(3)四个侧面中,是直角三角形的有 个;
(4)若AB=AD=AP,试在图中作出平面PDC的一个法向量.
DA,CB
AB=AD
4
在平面PAD中,过点A作AH⊥PD, 即为平面PDC的一个法向量.
H
例2:已知:如图,直三棱柱ABC-A'B'C'中,
点M,N分别为A'B和B'C'的中点.
(1)求证:MN∥平面A'ACC';(2)求证:平面CMN⊥平面A'MN.
证明:由直三棱柱ABC-A'B'C',可知A'A⊥平面ABC.
故以点A为原点,AB,AC,AA'所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
又
设AA'=1,
则
例2:已知:如图,直三棱柱ABC-A'B'C'中,
点M,N分别为A'B和B'C'的中点.
(1)求证:MN∥平面A'ACC';(2)求证:平面CMN⊥平面A'MN.
∵点M,N分别为A'B和B'C'的中点,
(1)由图易知 是平面A'ACC'的一个法向量.
∴ ∥平面 A'ACC'.
又∵ 平面A'ACC',∴MN∥平面A'ACC'.
例2:已知:如图,直三棱柱ABC-A'B'C'中,
点M,N分别为A'B和B'C'的中点.
(1)求证:MN∥平面A'ACC';(2)求证:平面CMN⊥平面A'MN.
(2)依题意有
设n1=(x,y,z)是平面CMN的一个法向量,
则
不妨取y=1,得
例2:已知:如图,直三棱柱ABC-A'B'C'中,
点M,N分别为A'B和B'C'的中点.
(1)求证:MN∥平面A'ACC';(2)求证:平面CMN⊥平面A'MN.
同理可得平面A'MN的一个法向量
∴平面CMN⊥平面A'MN.
归纳总结
利用空间向量解决立体几何问题的一般步骤
1.建立适当的空间直角坐标系,求对应点的坐标;
4.把向量运算的结果“翻译”为几何结论.
3.运用向量方法求解;
2.用坐标表示空间向量;
练一练
2.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是BB1,D1B1的中点.求证:EF⊥平面B1AC.
证明:设正方体的棱长为2,建立如图所示的空间直角坐标系,
设平面B1AC的法向量为n=(x,y,z),
则A(2,0,0),C(0,2,0),B1(2,2,2),E(2,2,1),F(1,1,2).
练一练
2.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是BB1,D1B1的中点.求证:EF⊥平面B1AC.
令x=1,则y=1,z=-1,
∴n=(1,1,-1),
∴EF⊥平面B1AC.
根据今天所学,回答下列问题:
1.三垂线定理及其逆定理分别是什么?
2.利用空间向量解决立体几何问题的一般步骤是什么?
3.4.2 第2课时
新授课
用向量方法研究立体几何中的位置关系
1.理解并掌握三垂线定理及其逆定理.
2.会用空间向量解决立体几何问题,掌握其一般步骤.
例1:已知:如图,AB⊥α,垂足为点B,
求证:l⊥AC.
证明:设向量l是直线l的方向向量.
由l⊥BC可知,
本例所证明的结论,通常称为三垂线定理.这里,直线BC实际上是斜线AC在平面α内的投影.
归纳总结
三垂线定理:若平面内的一条直线与平面的一条斜线在这个平面内的投影垂直,则它也和这条斜线垂直.
类似地可以得到:
三垂线定理的逆定理:若平面内的一条直线和这个平面的一条斜线垂直,则它也和这条斜线在这个平面内的投影垂直.
练一练
1.已知:如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD.
(1)所有棱中,与直线PB垂直的有 ;
(2)PC⊥BD的一个充要条件是 ;
(3)四个侧面中,是直角三角形的有 个;
(4)若AB=AD=AP,试在图中作出平面PDC的一个法向量.
DA,CB
AB=AD
4
在平面PAD中,过点A作AH⊥PD, 即为平面PDC的一个法向量.
H
例2:已知:如图,直三棱柱ABC-A'B'C'中,
点M,N分别为A'B和B'C'的中点.
(1)求证:MN∥平面A'ACC';(2)求证:平面CMN⊥平面A'MN.
证明:由直三棱柱ABC-A'B'C',可知A'A⊥平面ABC.
故以点A为原点,AB,AC,AA'所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
又
设AA'=1,
则
例2:已知:如图,直三棱柱ABC-A'B'C'中,
点M,N分别为A'B和B'C'的中点.
(1)求证:MN∥平面A'ACC';(2)求证:平面CMN⊥平面A'MN.
∵点M,N分别为A'B和B'C'的中点,
(1)由图易知 是平面A'ACC'的一个法向量.
∴ ∥平面 A'ACC'.
又∵ 平面A'ACC',∴MN∥平面A'ACC'.
例2:已知:如图,直三棱柱ABC-A'B'C'中,
点M,N分别为A'B和B'C'的中点.
(1)求证:MN∥平面A'ACC';(2)求证:平面CMN⊥平面A'MN.
(2)依题意有
设n1=(x,y,z)是平面CMN的一个法向量,
则
不妨取y=1,得
例2:已知:如图,直三棱柱ABC-A'B'C'中,
点M,N分别为A'B和B'C'的中点.
(1)求证:MN∥平面A'ACC';(2)求证:平面CMN⊥平面A'MN.
同理可得平面A'MN的一个法向量
∴平面CMN⊥平面A'MN.
归纳总结
利用空间向量解决立体几何问题的一般步骤
1.建立适当的空间直角坐标系,求对应点的坐标;
4.把向量运算的结果“翻译”为几何结论.
3.运用向量方法求解;
2.用坐标表示空间向量;
练一练
2.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是BB1,D1B1的中点.求证:EF⊥平面B1AC.
证明:设正方体的棱长为2,建立如图所示的空间直角坐标系,
设平面B1AC的法向量为n=(x,y,z),
则A(2,0,0),C(0,2,0),B1(2,2,2),E(2,2,1),F(1,1,2).
练一练
2.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是BB1,D1B1的中点.求证:EF⊥平面B1AC.
令x=1,则y=1,z=-1,
∴n=(1,1,-1),
∴EF⊥平面B1AC.
根据今天所学,回答下列问题:
1.三垂线定理及其逆定理分别是什么?
2.利用空间向量解决立体几何问题的一般步骤是什么?
同课章节目录
