北师大版高中数学选择性必修第一册 3.4.3第1课时用向量方法研究立体几何中的度量关系 课件(共16张PPT)
文档属性
| 名称 | 北师大版高中数学选择性必修第一册 3.4.3第1课时用向量方法研究立体几何中的度量关系 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 422.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 11:06:58 | ||
图片预览






文档简介
(共16张PPT)
3.4.3 第1课时
新授课
用向量方法研究立体几何中的度量关系
1.会用向量法求线线角、线面角.
2.能正确区分向量夹角与所求线线角、线面角的关系.
在必修课程中,我们学习过异面直线所成的角,直线与平面相交所成的角,以及两个平面相交所成的二面角.
那么,在空间中怎样描述这些角呢?这些角的大小与直线的方向向量、平面的法向量有何关系?
知识点1:两条直线所成的角
当两条直线平行时,规定它们所成的角为0;
当两条直线a与b是异面直线时,
在空间任取一点O,过点O作直线a'和b',使得a'∥a,b'∥b,
当两条直线a与b相交时,我们把两条直线交角中范围在 内的角叫作两条直线所成的角(如图①);
a
b
图①
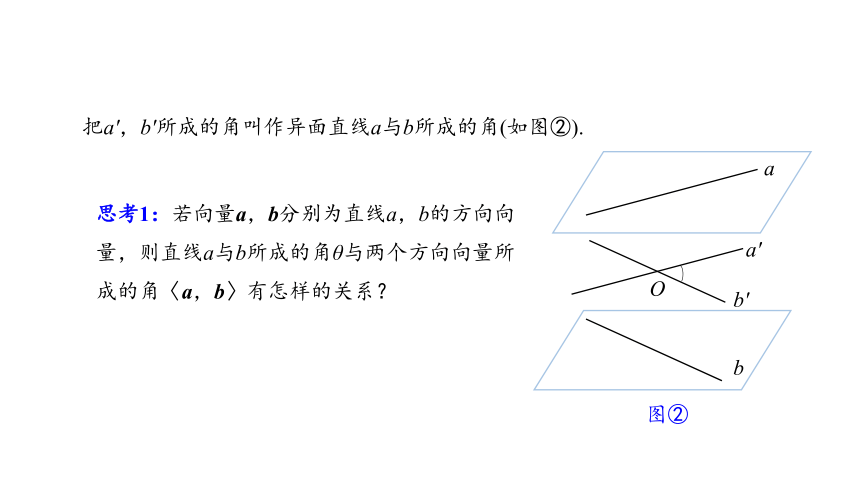
把a',b'所成的角叫作异面直线a与b所成的角(如图②).
图②
a
b
a'
b'
O
思考1:若向量a,b分别为直线a,b的方向向量,则直线a与b所成的角θ与两个方向向量所成的角〈a,b〉有怎样的关系?
归纳总结
若向量a,b分别为直线a,b的方向向量,则直线a与b所成的角θ∈
且θ与两个方向向量所成的角〈a,b〉相等或互补.
也就是说,当 时,
当 时,
故
cos θ=|cos〈a,b〉|.
例1:如图,在空间直角坐标系中有长方体ABCD-A'B'C'D',AB=2,BC=1,AA'=3.求AC'与A'D所成角的余弦值.
解:设s1,s2分别是AC'和A'D的一个方向向量,取
∵A(0,0,0),C'(2,1,3),A'(0,0,3),D(0,1,0),
设AC'与A'D所成角为θ,
故AC'与A'D所成角的余弦值为
则
练一练
1.如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,求B1M与D1N所成角的余弦值.
解:建立如图所示的空间直角坐标系,设正方体的棱长为2,
则B1(2,2,2),M(1,1,0),D1(0,0,2),N(1,0,0),
故AC'与A'D所成角的余弦值为
知识点2:直线和平面所成的角
平面的一条斜线和它在平面内的投影所成的锐角就是这条直线与这
个平面所成的角.
当一条直线与一个平面平行或在这个平面内时,规定这条直线与这个平面所成角的大小为0;
当一条直线与一个平面垂直时,规定这条直线与这个平面所成角的大小为
思考2:观察如图直线l的一个方向向量l与平面α的一个法向量n两者的夹角〈l,n〉与直线l和平面α所成的角θ的关系是什么?
归纳总结
设向量l为直线l的一个方向向量,n是平面α的一个法向量,
故
sin θ=|cos〈l,n〉|.
则直线l与平面α所成的角θ∈
且θ= 或θ=
解:由正三棱柱知AA'⊥平面ABC,故以点A为原点,AC,AA'所在直线分别为y轴、z轴,如图建立空间直角坐标系.
易知n=(1,0,0)是平面ACC'A'的一个法向量.
由△ABC是边长为2的正三角形,可得
例2:如图,在正三棱柱ABC-A'B'C'中,底面边长为2,AA'= ,求直线AB'与侧面ACC'A'所成角的正弦值.
设直线AB'与侧面ACC'A'所成角为θ,
故直线AB'与侧面ACC'A'所成角的正弦值为
则
例2:如图,在正三棱柱ABC-A'B'C'中,底面边长为2,AA'= ,求直线AB'与侧面ACC'A'所成角的正弦值.
归纳总结
利用平面的法向量求直线与平面夹角的基本步骤
(1)建立空间直角坐标系.
(2)求直线的方向向量u.
(3)求平面的法向量n.
(4)设线面角为θ,则sin θ=
练一练
解:平面α的一个法向量n=(2,1,1),直线l的一个方向向量为a=(1,2,3),
2.若平面α的一个法向量n=(2,1,1),直线l的一个方向向量为a=(1,2,3),则l与α所成角的正弦值为( )
A. B. C. D.
∴l与α所成角的正弦值为
B
根据今天所学,回答下列问题:
1.如何用向量法求空间内的线线、线面夹角?
3.4.3 第1课时
新授课
用向量方法研究立体几何中的度量关系
1.会用向量法求线线角、线面角.
2.能正确区分向量夹角与所求线线角、线面角的关系.
在必修课程中,我们学习过异面直线所成的角,直线与平面相交所成的角,以及两个平面相交所成的二面角.
那么,在空间中怎样描述这些角呢?这些角的大小与直线的方向向量、平面的法向量有何关系?
知识点1:两条直线所成的角
当两条直线平行时,规定它们所成的角为0;
当两条直线a与b是异面直线时,
在空间任取一点O,过点O作直线a'和b',使得a'∥a,b'∥b,
当两条直线a与b相交时,我们把两条直线交角中范围在 内的角叫作两条直线所成的角(如图①);
a
b
图①
把a',b'所成的角叫作异面直线a与b所成的角(如图②).
图②
a
b
a'
b'
O
思考1:若向量a,b分别为直线a,b的方向向量,则直线a与b所成的角θ与两个方向向量所成的角〈a,b〉有怎样的关系?
归纳总结
若向量a,b分别为直线a,b的方向向量,则直线a与b所成的角θ∈
且θ与两个方向向量所成的角〈a,b〉相等或互补.
也就是说,当 时,
当 时,
故
cos θ=|cos〈a,b〉|.
例1:如图,在空间直角坐标系中有长方体ABCD-A'B'C'D',AB=2,BC=1,AA'=3.求AC'与A'D所成角的余弦值.
解:设s1,s2分别是AC'和A'D的一个方向向量,取
∵A(0,0,0),C'(2,1,3),A'(0,0,3),D(0,1,0),
设AC'与A'D所成角为θ,
故AC'与A'D所成角的余弦值为
则
练一练
1.如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,求B1M与D1N所成角的余弦值.
解:建立如图所示的空间直角坐标系,设正方体的棱长为2,
则B1(2,2,2),M(1,1,0),D1(0,0,2),N(1,0,0),
故AC'与A'D所成角的余弦值为
知识点2:直线和平面所成的角
平面的一条斜线和它在平面内的投影所成的锐角就是这条直线与这
个平面所成的角.
当一条直线与一个平面平行或在这个平面内时,规定这条直线与这个平面所成角的大小为0;
当一条直线与一个平面垂直时,规定这条直线与这个平面所成角的大小为
思考2:观察如图直线l的一个方向向量l与平面α的一个法向量n两者的夹角〈l,n〉与直线l和平面α所成的角θ的关系是什么?
归纳总结
设向量l为直线l的一个方向向量,n是平面α的一个法向量,
故
sin θ=|cos〈l,n〉|.
则直线l与平面α所成的角θ∈
且θ= 或θ=
解:由正三棱柱知AA'⊥平面ABC,故以点A为原点,AC,AA'所在直线分别为y轴、z轴,如图建立空间直角坐标系.
易知n=(1,0,0)是平面ACC'A'的一个法向量.
由△ABC是边长为2的正三角形,可得
例2:如图,在正三棱柱ABC-A'B'C'中,底面边长为2,AA'= ,求直线AB'与侧面ACC'A'所成角的正弦值.
设直线AB'与侧面ACC'A'所成角为θ,
故直线AB'与侧面ACC'A'所成角的正弦值为
则
例2:如图,在正三棱柱ABC-A'B'C'中,底面边长为2,AA'= ,求直线AB'与侧面ACC'A'所成角的正弦值.
归纳总结
利用平面的法向量求直线与平面夹角的基本步骤
(1)建立空间直角坐标系.
(2)求直线的方向向量u.
(3)求平面的法向量n.
(4)设线面角为θ,则sin θ=
练一练
解:平面α的一个法向量n=(2,1,1),直线l的一个方向向量为a=(1,2,3),
2.若平面α的一个法向量n=(2,1,1),直线l的一个方向向量为a=(1,2,3),则l与α所成角的正弦值为( )
A. B. C. D.
∴l与α所成角的正弦值为
B
根据今天所学,回答下列问题:
1.如何用向量法求空间内的线线、线面夹角?
同课章节目录
