北师大版高中数学选择性必修第一册 3.4.2第1课时用向量方法研究立体几何中的位置关系 课件(共18张PPT)
文档属性
| 名称 | 北师大版高中数学选择性必修第一册 3.4.2第1课时用向量方法研究立体几何中的位置关系 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 11:08:59 | ||
图片预览




文档简介
(共18张PPT)
3.4.2 第1课时
新授课
用向量方法研究立体几何中的位置关系
1.能用向量语言表述直线与直线、直线与平面、平面与平面平行与垂直的关系.
2.理解用向量方法证明直线、平面间的平行与垂直的关系不同思路.
思考:平行和垂直是立体几何中主要的位置关系,那么如何用向量方法进行研究呢?
知识点:用向量方法研究立体几何中的位置关系
思考1:由直线与直线的平行关系, 可以得到这两条直线的方向向量有什么关系呢?
设l,m分别是直线l,m的方向向量,
使得
l
l
m
m
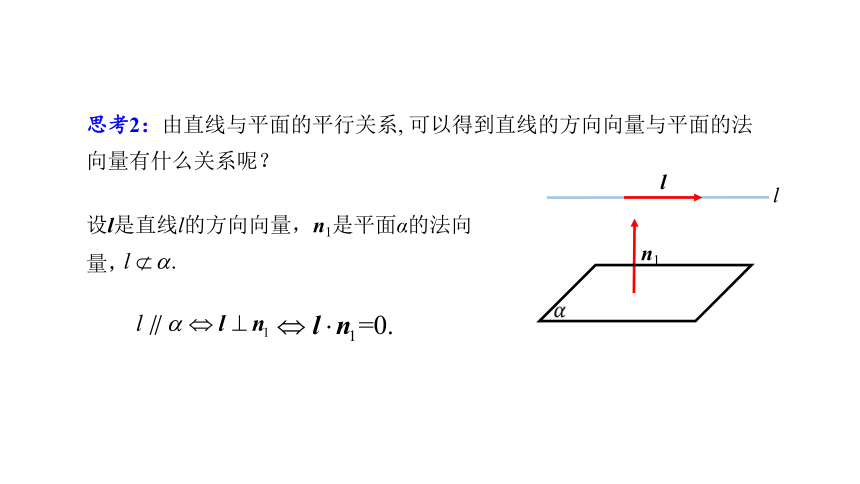
思考2:由直线与平面的平行关系, 可以得到直线的方向向量与平面的法向量有什么关系呢?
设l是直线l的方向向量,n1是平面α的法向量,
l
n1
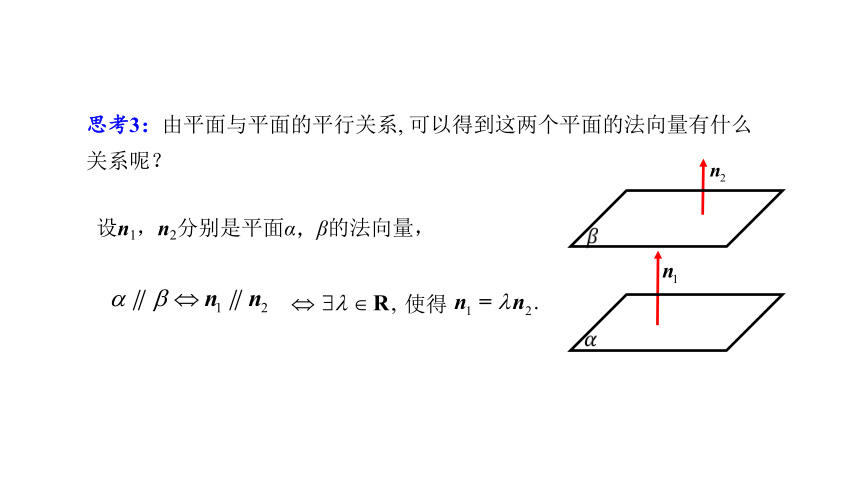
思考3:由平面与平面的平行关系, 可以得到这两个平面的法向量有什么关系呢?
设n1,n2分别是平面α,β的法向量,
使得
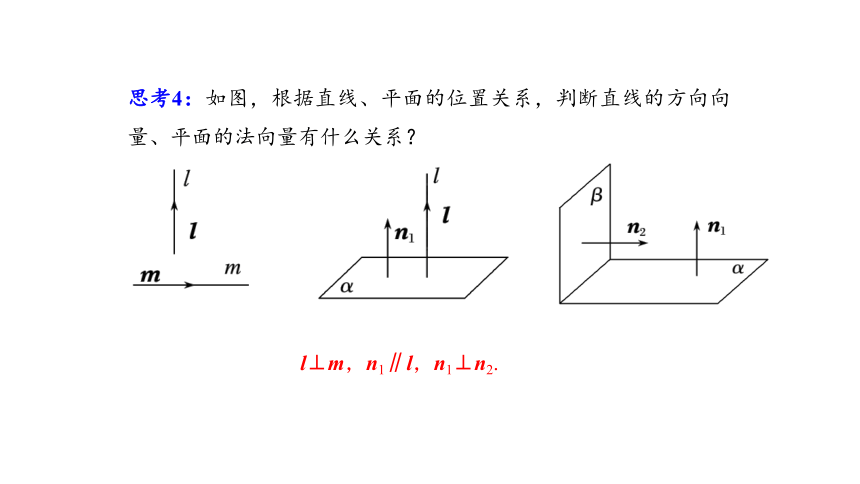
思考4:如图,根据直线、平面的位置关系,判断直线的方向向量、平面的法向量有什么关系?
l⊥m,n1∥l,n1⊥n2.
设向量l,m分别是直线l,m的方向向量,n1,n2分别是平面α,β的法向量,用直线的方向向量和平面的法向量表达下列各种位置关系.
几何关系 向量语言
l∥m
l∥α
α∥β
l⊥m
l⊥α
α⊥β
思路1 若只从直线的方向向量和平面的法向量入手考虑,设向量l是直线l的方向向量,n1是平面α的法向量,则只需证明l⊥n1.
想一想:请从不同角度用向量方法证明l∥α.
思路2 考虑向量与平面平行的定义,以及平面向量基本定理,从而得到:将直线l的方向向量l用平面α的一组基线性表示,此时必有l∥α.
由此可知,运用向量证明几何问题的方法,一方面源于立体几何中定理的向量化表述, 另一方面也需要结合向量自身的特点.
思路3 直接将线面平行的判定定理向量化,找到m α,且直线l与m的方向向量共线.
归纳总结
设向量l,m分别是直线l,m的方向向量,n1,n2分别是平面α,β的法向量,则
l∥m或l与m重合
l∥α或
α∥β或α与β重合
1.设直线l的方向向量是a,平面α的法向量是n,则“a⊥n”是“l∥α”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:由l∥α,得a⊥n,
则“a⊥n”是“l∥α”的必要条件,
而a⊥n不一定有l∥α,也可能l α,
则“a⊥n”不是“l∥α”的充分条件.
B
练一练
分析:设m是平面α内的任意一条直线.要证明n⊥α,只需证明n⊥m.如何充分运用条件,表达“m是平面α内的任意一条直线”呢?可以考虑将直线m的方向向量用平面α的一组基表示.
α
n
a
b
m
例1:证明“直线与平面垂直的判定定理”:如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.
已知:如图,a,b是平面α内的两条相交直线,直线n⊥a,且n⊥b.
求证:n⊥α.
例1:证明“直线与平面垂直的判定定理”:如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.
已知:如图,a,b是平面α内的两条相交直线,直线n⊥a,且n⊥b.
求证:n⊥α.
证明:设m是平面α内的任意一条直线.
α
n
a
b
m
a,b,m,n依次为直线a,b,m,n的方向向量,
∵直线a,b相交,∴向量a,b不共线.
在平面α内,根据平面向量基本定理可知存在唯一的实数对(x,y)使得m=xa+yb,
∴n·m=xn·a+yn·b.
α
n
a
b
m
∵n⊥a,且n⊥b,
∴n·a=0,n·b=0,
∴n⊥α.
∴n·m=0,故n⊥m.
例1:证明“直线与平面垂直的判定定理”:如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.
已知:如图,a,b是平面α内的两条相交直线,直线n⊥a,且n⊥b.
求证:n⊥α.
练一练
2.证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:如图, 求证:
证明:取直线l的方向向量u,平面β的法向量n.
∵ ∴u是平面α的法向量.
∵ 而n是平面β的法向量,∴u⊥n.
∴
例2:证明“两个平面平行的判定定理”:如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行.
已知:如图,a,b是平面α内的两条相交直线,且a∥β,b∥β.
求证:α∥β.
证明:设向量a,b分别是直线a,b的方向向量.
α
a
b
∵a∥β,b∥β,∴a∥β,b∥β.
设n是平面β的法向量,则n⊥a,n⊥b.
∴n⊥α,∴α∥β.
∵a,b是平面α内的两条相交直线,
β
n
根据今天所学,完成下列表格:
几何关系 向量语言
l∥m
l∥α
α∥β
l⊥m
l⊥α
α⊥β
设向量l,m分别是直线l,m的方向向量,n1,n2分别是平面α,β的法向量,则
3.4.2 第1课时
新授课
用向量方法研究立体几何中的位置关系
1.能用向量语言表述直线与直线、直线与平面、平面与平面平行与垂直的关系.
2.理解用向量方法证明直线、平面间的平行与垂直的关系不同思路.
思考:平行和垂直是立体几何中主要的位置关系,那么如何用向量方法进行研究呢?
知识点:用向量方法研究立体几何中的位置关系
思考1:由直线与直线的平行关系, 可以得到这两条直线的方向向量有什么关系呢?
设l,m分别是直线l,m的方向向量,
使得
l
l
m
m
思考2:由直线与平面的平行关系, 可以得到直线的方向向量与平面的法向量有什么关系呢?
设l是直线l的方向向量,n1是平面α的法向量,
l
n1
思考3:由平面与平面的平行关系, 可以得到这两个平面的法向量有什么关系呢?
设n1,n2分别是平面α,β的法向量,
使得
思考4:如图,根据直线、平面的位置关系,判断直线的方向向量、平面的法向量有什么关系?
l⊥m,n1∥l,n1⊥n2.
设向量l,m分别是直线l,m的方向向量,n1,n2分别是平面α,β的法向量,用直线的方向向量和平面的法向量表达下列各种位置关系.
几何关系 向量语言
l∥m
l∥α
α∥β
l⊥m
l⊥α
α⊥β
思路1 若只从直线的方向向量和平面的法向量入手考虑,设向量l是直线l的方向向量,n1是平面α的法向量,则只需证明l⊥n1.
想一想:请从不同角度用向量方法证明l∥α.
思路2 考虑向量与平面平行的定义,以及平面向量基本定理,从而得到:将直线l的方向向量l用平面α的一组基线性表示,此时必有l∥α.
由此可知,运用向量证明几何问题的方法,一方面源于立体几何中定理的向量化表述, 另一方面也需要结合向量自身的特点.
思路3 直接将线面平行的判定定理向量化,找到m α,且直线l与m的方向向量共线.
归纳总结
设向量l,m分别是直线l,m的方向向量,n1,n2分别是平面α,β的法向量,则
l∥m或l与m重合
l∥α或
α∥β或α与β重合
1.设直线l的方向向量是a,平面α的法向量是n,则“a⊥n”是“l∥α”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
解析:由l∥α,得a⊥n,
则“a⊥n”是“l∥α”的必要条件,
而a⊥n不一定有l∥α,也可能l α,
则“a⊥n”不是“l∥α”的充分条件.
B
练一练
分析:设m是平面α内的任意一条直线.要证明n⊥α,只需证明n⊥m.如何充分运用条件,表达“m是平面α内的任意一条直线”呢?可以考虑将直线m的方向向量用平面α的一组基表示.
α
n
a
b
m
例1:证明“直线与平面垂直的判定定理”:如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.
已知:如图,a,b是平面α内的两条相交直线,直线n⊥a,且n⊥b.
求证:n⊥α.
例1:证明“直线与平面垂直的判定定理”:如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.
已知:如图,a,b是平面α内的两条相交直线,直线n⊥a,且n⊥b.
求证:n⊥α.
证明:设m是平面α内的任意一条直线.
α
n
a
b
m
a,b,m,n依次为直线a,b,m,n的方向向量,
∵直线a,b相交,∴向量a,b不共线.
在平面α内,根据平面向量基本定理可知存在唯一的实数对(x,y)使得m=xa+yb,
∴n·m=xn·a+yn·b.
α
n
a
b
m
∵n⊥a,且n⊥b,
∴n·a=0,n·b=0,
∴n⊥α.
∴n·m=0,故n⊥m.
例1:证明“直线与平面垂直的判定定理”:如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.
已知:如图,a,b是平面α内的两条相交直线,直线n⊥a,且n⊥b.
求证:n⊥α.
练一练
2.证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:如图, 求证:
证明:取直线l的方向向量u,平面β的法向量n.
∵ ∴u是平面α的法向量.
∵ 而n是平面β的法向量,∴u⊥n.
∴
例2:证明“两个平面平行的判定定理”:如果一个平面内的两条相交直线与另一个平面平行,那么这两个平面平行.
已知:如图,a,b是平面α内的两条相交直线,且a∥β,b∥β.
求证:α∥β.
证明:设向量a,b分别是直线a,b的方向向量.
α
a
b
∵a∥β,b∥β,∴a∥β,b∥β.
设n是平面β的法向量,则n⊥a,n⊥b.
∴n⊥α,∴α∥β.
∵a,b是平面α内的两条相交直线,
β
n
根据今天所学,完成下列表格:
几何关系 向量语言
l∥m
l∥α
α∥β
l⊥m
l⊥α
α⊥β
设向量l,m分别是直线l,m的方向向量,n1,n2分别是平面α,β的法向量,则
同课章节目录
