北师大版高中数学选择性必修第一册 5.1.2基本计数原理的简单应用(1)课件(共13张PPT)
文档属性
| 名称 | 北师大版高中数学选择性必修第一册 5.1.2基本计数原理的简单应用(1)课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 780.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 11:12:29 | ||
图片预览



文档简介
(共13张PPT)
第五章 计数原理
5.1.3 基本计数原理的简单应用(1)
1.理解基本计数原理,能正确区分“类”和“步”;
2.理解分类加法计数原理和分步乘法计数原理的区别和联系.
正确选择加法原理或乘法原理解决问题.
理解两个计数原理的区别和联系.
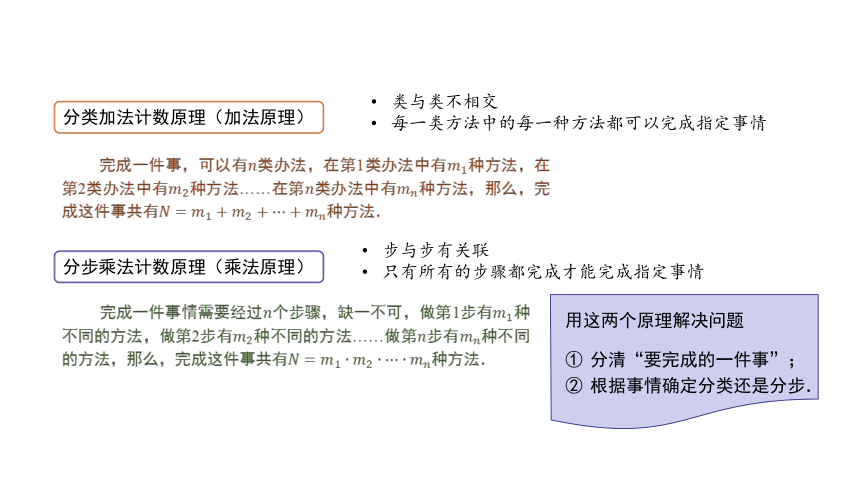
分步乘法计数原理(乘法原理)
分类加法计数原理(加法原理)
类与类不相交
每一类方法中的每一种方法都可以完成指定事情
步与步有关联
只有所有的步骤都完成才能完成指定事情
分清“要完成的一件事”;
根据事情确定分类还是分步.
用这两个原理解决问题
①能够被5整除的数的特征是什么?
②该问题中需要完成的“一件事”是什么?
③如何完成“这件事”?
末位数字是0或5
确定自然数1~200中末位是0或5的数的个数
分末位是0和末位是5两类进行计数
解:能够被5整除的数,末位数字是0或5,因此,我们把1,2,3.…,200中能够被5整除的数分成2类来计数:
第1类,末位数字是0的数,共有20个;
第2类,末位数字是5的数,共有20个.
根据分类加法计数原理,在1,2,3.…,200中,能够被5整除的数共有N=20+20=40个.
本题能够顺利求解的关键是什么?
准确指出问题中的“一件事”;
按照明确的标准给问题分类.
在1,2,3,…,200中,能够被5整除的数共有多少个?
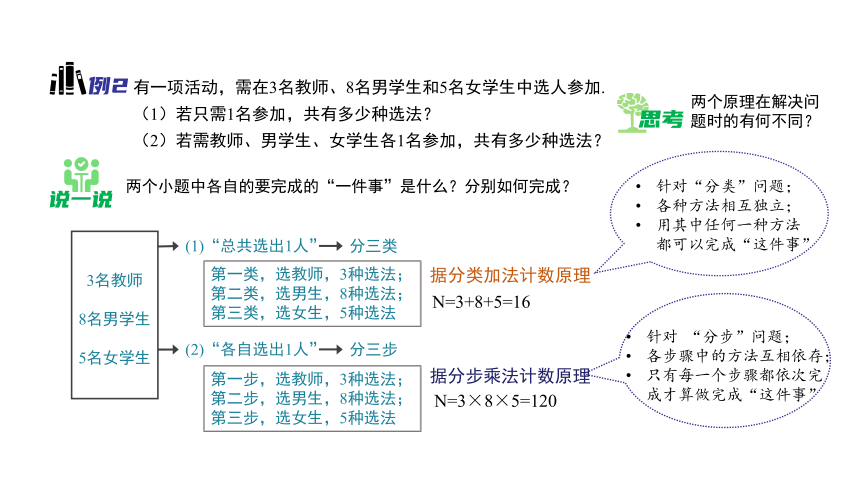
有一项活动,需在3名教师、8名男学生和5名女学生中选人参加.
(1)若只需1名参加,共有多少种选法?
(2)若需教师、男学生、女学生各1名参加,共有多少种选法?
两个小题中各自的要完成的“一件事”是什么?分别如何完成?
(1)“总共选出1人”
(2)“各自选出1人”
3名教师
8名男学生
5名女学生
分三类
分三步
第一类,选教师,3种选法;
第二类,选男生,8种选法;
第三类,选女生,5种选法
第一步,选教师,3种选法;
第二步,选男生,8种选法;
第三步,选女生,5种选法
N=3×8×5=120
据分步乘法计数原理
N=3+8+5=16
据分类加法计数原理
针对“分类”问题;
各种方法相互独立;
用其中任何一种方法都可以完成“这件事”
两个原理在解决问题时的有何不同?
针对 “分步”问题;
各步骤中的方法互相依存;
只有每一个步骤都依次完成才算做完成“这件事”
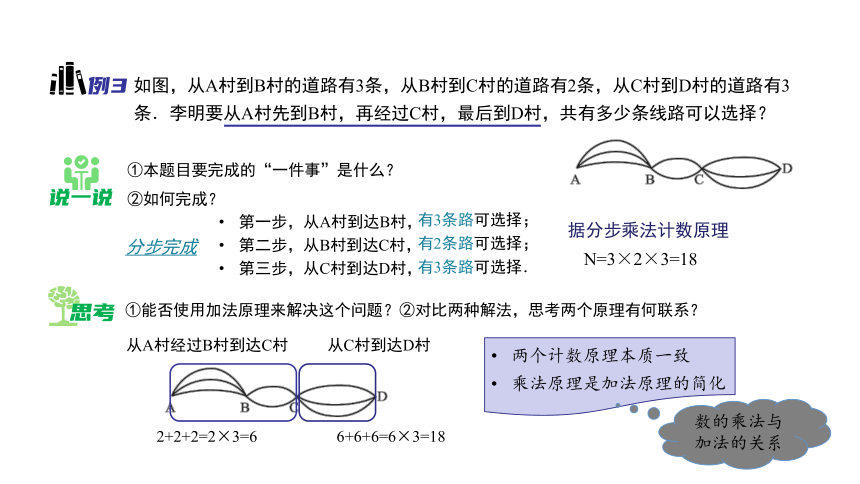
如图,从A村到B村的道路有3条,从B村到C村的道路有2条,从C村到D村的道路有3条.李明要从A村先到B村,再经过C村,最后到D村,共有多少条线路可以选择?
①本题目要完成的“一件事”是什么?
②如何完成?
第一步,从A村到达B村,
第二步,从B村到达C村,
第三步,从C村到达D村,
分步完成
有3条路可选择;
有2条路可选择;
有3条路可选择.
N=3×2×3=18
据分步乘法计数原理
①能否使用加法原理来解决这个问题?②对比两种解法,思考两个原理有何联系?
从A村经过B村到达C村
2+2+2=2×3=6
从C村到达D村
6+6+6=6×3=18
两个计数原理本质一致
乘法原理是加法原理的简化
数的乘法与加法的关系
要给如图所示的五个区域涂色,现有四种颜色可供选择,要求每个区域只涂一种颜色,且相邻区域所涂颜色不相同,则不同的涂色方案一共有多少种?
D
A
B
C
E
①本题目要完成的“一件事”是什么?
②如何完成?
“用四种颜色给如图所示的五个区域涂色,且相邻区域不同色”
理清关系,按区域分步
第一类,A、C同色:
第一步,给区域A涂色,有4种选择;
第二步,给区域C涂色,有1中选择;
第三步,给区域B涂色,有3种选择;
第四步,给区域E涂色,有2种选择;
第五步,给区域D涂色,有2种选择.
则根据分步乘法计数原理,
一共有为4×1×3×2×2=48种不同的选择;
第二类,A、C异色:
第一步,给区域A涂色,有4种选择;
第二步,给区域C涂色,有3种选择;
第三步,给区域B涂色,有2种选择;
第四步,给区域E涂色,只有1种选择;
第五步,给区域D涂色,只有1种选择.
则根据分步乘法计数原理,
一共有为4×3×2×1×1=24种不同选择;
综上,根据分类加法计数原理,该图形的不同涂色方案共有48+24=72种.
解:按A与C颜色的相同和相异分类求解.
要给如图所示的五个区域涂色,现有四种颜色可供选择,要求每个区域只涂一种颜色,且相邻区域所涂颜色不相同,则不同的涂色方案一共有多少种?
D
A
B
C
E
你还有其他解决这个问题的方法吗?
提示:看位置关系——A、C对角,B、D对角
此时先确定A、C的颜色,有4种可能,再确定B、D的颜色,有3种可能,再确定E的颜色,有2种可能,所以共有4×3×2=24种不同的可能.
第一类:A、C同色,B、D不同色,
第二类:A、C不同色,B、D同色,
第三类:A、C同色,B、D同色,
此时先确定A、C的颜色,有4种可能,再依次确定B、E、D的颜色,分别有3,2,1种可能,所以共有4×3×2×1=24种不同的可能;
方法同第一类,也共有24种不同的可能;
根据分类加法计数原理,该图形不同的涂色方案共有24+24+24=72种.
有10本不同的数学书,9本不同的语文书,8本不同的英语书,从中取出数学书、语文书、英语书各1本,共有多少种取法?
解:第一步,取出1本数学书,共有10种取法,
第二步,取出1本语文书,共有9种取法,
第三步,取出1本英语书,共有8种取法,
根据分步乘法计数原理,共有N=10×9×8=720种取法.
要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,共有多少种不同的挂法?
方法一,分类解决这个问题,
第一类,“甲在左”时,不同的挂法有“甲乙、甲丙”2种;
第二类,“乙在左”时,不同的挂法有“乙甲、乙丙”2种;
第三类, “丙在左”时,不同的挂法有 “丙甲、丙乙”2种.
所以不同的挂法共有2+2+2=6种.
方法三,先选出两幅画,再按指定位置挂好.
第一步,从3幅画中选出2幅,有3种选法:甲乙、甲丙、乙丙;
第二步,将选出的两幅画挂好,分别有2种挂法.
所以共有3×2=6种挂法.
方法二,从3幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:
第1步,从3幅画中选1幅挂在左边墙上,有3种选法;
第2步,从剩下的2幅画中选1幅挂在右边墙上,有2种选法.
根据分步乘法计数原理,不同挂法的种数为N=3×2=6.
选1幅挂左边
选1幅挂右边
甲
乙
丙
甲
乙
丙
甲
乙
丙
方法二
甲、乙
甲、丙
乙、丙
甲丙
甲乙
乙甲
乙丙
丙乙
丙甲
方法三
分类加法计数原理 分步乘法计数原理
区别 完成一件事,共有n类方法,关键词是“分类” . 完成一件事,共有n个步骤,关键词是“分步” .
每类方法都能独立完成这件事,且每类方法得到的都是最后结果,只需一种方法就可以完成这件事. 任何一步都不能独立完成这件事,缺少任何一步也不能完成这件事,只有各个步骤都完成了,才能完成这件事.
各类方法之间是互斥的、并列的、独立的. 各步之间是关联的、独立的,“关联”确保不遗漏,“独立”确保不重复.
联系 都是求完成一件事情的方法种数.
本质一样,乘法原理可以看成是加法原理的简化,类似于数的运算中乘法是加法的简化.
解决实际问题时常常需要两个原理结合应用.
简单总结一下两个计数原理的区别和联系.
计算前
仔细分析
(1)明确要完成的“一件事”是什么; (2)明确需要分类还是分步.
计算中
分类要做到“不重不漏”——分类后再分别对每一类进行计数(可能需要分步),最后用分类加法计数原理求和,得到总数.
分步要做到“步骤完整”——完成了所有步骤,恰好完成任务,当然步与步之间要相互独立.分步后再计算每一步的方法数(可能需要分类),最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
回顾用两个计数原理解决计数问题的过程,尝试说一说其中的要点都有哪些?
教材P158,习题5-1,A组第1,2,3,4题
第五章 计数原理
5.1.3 基本计数原理的简单应用(1)
1.理解基本计数原理,能正确区分“类”和“步”;
2.理解分类加法计数原理和分步乘法计数原理的区别和联系.
正确选择加法原理或乘法原理解决问题.
理解两个计数原理的区别和联系.
分步乘法计数原理(乘法原理)
分类加法计数原理(加法原理)
类与类不相交
每一类方法中的每一种方法都可以完成指定事情
步与步有关联
只有所有的步骤都完成才能完成指定事情
分清“要完成的一件事”;
根据事情确定分类还是分步.
用这两个原理解决问题
①能够被5整除的数的特征是什么?
②该问题中需要完成的“一件事”是什么?
③如何完成“这件事”?
末位数字是0或5
确定自然数1~200中末位是0或5的数的个数
分末位是0和末位是5两类进行计数
解:能够被5整除的数,末位数字是0或5,因此,我们把1,2,3.…,200中能够被5整除的数分成2类来计数:
第1类,末位数字是0的数,共有20个;
第2类,末位数字是5的数,共有20个.
根据分类加法计数原理,在1,2,3.…,200中,能够被5整除的数共有N=20+20=40个.
本题能够顺利求解的关键是什么?
准确指出问题中的“一件事”;
按照明确的标准给问题分类.
在1,2,3,…,200中,能够被5整除的数共有多少个?
有一项活动,需在3名教师、8名男学生和5名女学生中选人参加.
(1)若只需1名参加,共有多少种选法?
(2)若需教师、男学生、女学生各1名参加,共有多少种选法?
两个小题中各自的要完成的“一件事”是什么?分别如何完成?
(1)“总共选出1人”
(2)“各自选出1人”
3名教师
8名男学生
5名女学生
分三类
分三步
第一类,选教师,3种选法;
第二类,选男生,8种选法;
第三类,选女生,5种选法
第一步,选教师,3种选法;
第二步,选男生,8种选法;
第三步,选女生,5种选法
N=3×8×5=120
据分步乘法计数原理
N=3+8+5=16
据分类加法计数原理
针对“分类”问题;
各种方法相互独立;
用其中任何一种方法都可以完成“这件事”
两个原理在解决问题时的有何不同?
针对 “分步”问题;
各步骤中的方法互相依存;
只有每一个步骤都依次完成才算做完成“这件事”
如图,从A村到B村的道路有3条,从B村到C村的道路有2条,从C村到D村的道路有3条.李明要从A村先到B村,再经过C村,最后到D村,共有多少条线路可以选择?
①本题目要完成的“一件事”是什么?
②如何完成?
第一步,从A村到达B村,
第二步,从B村到达C村,
第三步,从C村到达D村,
分步完成
有3条路可选择;
有2条路可选择;
有3条路可选择.
N=3×2×3=18
据分步乘法计数原理
①能否使用加法原理来解决这个问题?②对比两种解法,思考两个原理有何联系?
从A村经过B村到达C村
2+2+2=2×3=6
从C村到达D村
6+6+6=6×3=18
两个计数原理本质一致
乘法原理是加法原理的简化
数的乘法与加法的关系
要给如图所示的五个区域涂色,现有四种颜色可供选择,要求每个区域只涂一种颜色,且相邻区域所涂颜色不相同,则不同的涂色方案一共有多少种?
D
A
B
C
E
①本题目要完成的“一件事”是什么?
②如何完成?
“用四种颜色给如图所示的五个区域涂色,且相邻区域不同色”
理清关系,按区域分步
第一类,A、C同色:
第一步,给区域A涂色,有4种选择;
第二步,给区域C涂色,有1中选择;
第三步,给区域B涂色,有3种选择;
第四步,给区域E涂色,有2种选择;
第五步,给区域D涂色,有2种选择.
则根据分步乘法计数原理,
一共有为4×1×3×2×2=48种不同的选择;
第二类,A、C异色:
第一步,给区域A涂色,有4种选择;
第二步,给区域C涂色,有3种选择;
第三步,给区域B涂色,有2种选择;
第四步,给区域E涂色,只有1种选择;
第五步,给区域D涂色,只有1种选择.
则根据分步乘法计数原理,
一共有为4×3×2×1×1=24种不同选择;
综上,根据分类加法计数原理,该图形的不同涂色方案共有48+24=72种.
解:按A与C颜色的相同和相异分类求解.
要给如图所示的五个区域涂色,现有四种颜色可供选择,要求每个区域只涂一种颜色,且相邻区域所涂颜色不相同,则不同的涂色方案一共有多少种?
D
A
B
C
E
你还有其他解决这个问题的方法吗?
提示:看位置关系——A、C对角,B、D对角
此时先确定A、C的颜色,有4种可能,再确定B、D的颜色,有3种可能,再确定E的颜色,有2种可能,所以共有4×3×2=24种不同的可能.
第一类:A、C同色,B、D不同色,
第二类:A、C不同色,B、D同色,
第三类:A、C同色,B、D同色,
此时先确定A、C的颜色,有4种可能,再依次确定B、E、D的颜色,分别有3,2,1种可能,所以共有4×3×2×1=24种不同的可能;
方法同第一类,也共有24种不同的可能;
根据分类加法计数原理,该图形不同的涂色方案共有24+24+24=72种.
有10本不同的数学书,9本不同的语文书,8本不同的英语书,从中取出数学书、语文书、英语书各1本,共有多少种取法?
解:第一步,取出1本数学书,共有10种取法,
第二步,取出1本语文书,共有9种取法,
第三步,取出1本英语书,共有8种取法,
根据分步乘法计数原理,共有N=10×9×8=720种取法.
要从甲、乙、丙3幅不同的画中选出2幅,分别挂在左、右两边墙上的指定位置,共有多少种不同的挂法?
方法一,分类解决这个问题,
第一类,“甲在左”时,不同的挂法有“甲乙、甲丙”2种;
第二类,“乙在左”时,不同的挂法有“乙甲、乙丙”2种;
第三类, “丙在左”时,不同的挂法有 “丙甲、丙乙”2种.
所以不同的挂法共有2+2+2=6种.
方法三,先选出两幅画,再按指定位置挂好.
第一步,从3幅画中选出2幅,有3种选法:甲乙、甲丙、乙丙;
第二步,将选出的两幅画挂好,分别有2种挂法.
所以共有3×2=6种挂法.
方法二,从3幅画中选出2幅分别挂在左、右两边墙上,可以分两个步骤完成:
第1步,从3幅画中选1幅挂在左边墙上,有3种选法;
第2步,从剩下的2幅画中选1幅挂在右边墙上,有2种选法.
根据分步乘法计数原理,不同挂法的种数为N=3×2=6.
选1幅挂左边
选1幅挂右边
甲
乙
丙
甲
乙
丙
甲
乙
丙
方法二
甲、乙
甲、丙
乙、丙
甲丙
甲乙
乙甲
乙丙
丙乙
丙甲
方法三
分类加法计数原理 分步乘法计数原理
区别 完成一件事,共有n类方法,关键词是“分类” . 完成一件事,共有n个步骤,关键词是“分步” .
每类方法都能独立完成这件事,且每类方法得到的都是最后结果,只需一种方法就可以完成这件事. 任何一步都不能独立完成这件事,缺少任何一步也不能完成这件事,只有各个步骤都完成了,才能完成这件事.
各类方法之间是互斥的、并列的、独立的. 各步之间是关联的、独立的,“关联”确保不遗漏,“独立”确保不重复.
联系 都是求完成一件事情的方法种数.
本质一样,乘法原理可以看成是加法原理的简化,类似于数的运算中乘法是加法的简化.
解决实际问题时常常需要两个原理结合应用.
简单总结一下两个计数原理的区别和联系.
计算前
仔细分析
(1)明确要完成的“一件事”是什么; (2)明确需要分类还是分步.
计算中
分类要做到“不重不漏”——分类后再分别对每一类进行计数(可能需要分步),最后用分类加法计数原理求和,得到总数.
分步要做到“步骤完整”——完成了所有步骤,恰好完成任务,当然步与步之间要相互独立.分步后再计算每一步的方法数(可能需要分类),最后根据分步乘法计数原理,把完成每一步的方法数相乘,得到总数.
回顾用两个计数原理解决计数问题的过程,尝试说一说其中的要点都有哪些?
教材P158,习题5-1,A组第1,2,3,4题
同课章节目录
