北师大版高中数学选择性必修第一册 5.2.1排列与排列数 课件(共20张PPT)
文档属性
| 名称 | 北师大版高中数学选择性必修第一册 5.2.1排列与排列数 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
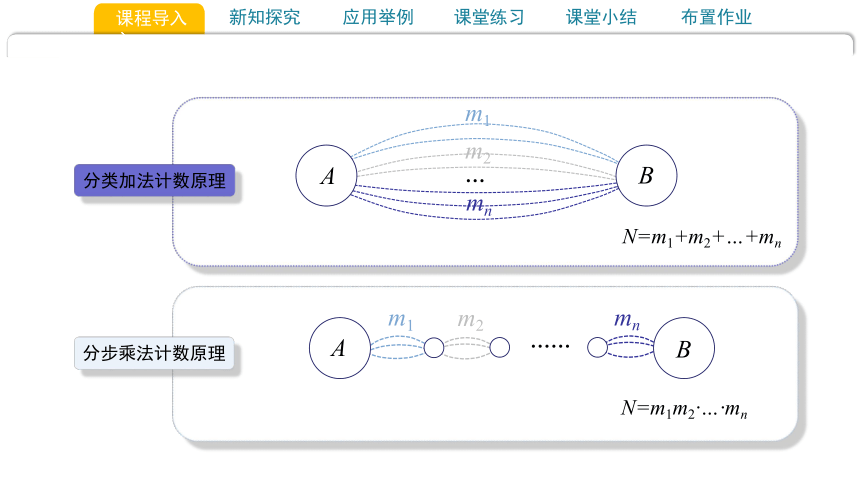
分类加法计数原理
…
m1
m2
mn
N=m1+m2+…+mn
分步乘法计数原理
……
m1
m2
mn
N=m1m2·…·mn
A
B
A
B
课程导入入
新知探究
应用举例
课堂练习
课堂小结
布置作业
在日常生活中,我们经常遇到下面一些问题,这些问题有什么共同特征呢?
(1)3名同学排成一行照相,共有多少种排法?
(2)北京、广州、南京、武汉4个城市相互通航,请列举出所有机票的情况,
并指出共有多少种机票.
(3)从4面不同颜色(红、黄、蓝、绿)的旗子中, 选出3面排成一排作为一 种信号,共能组成多少种信号?
课程导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
3名同学排成一行照相,共有多少种排法?
确定要完成的一件事是什么?
怎样完成这件事?分类 or 分步?
分步
第1步,确定排在第一个位置的同学;
A、B、C
第一位
A
B
C
3种选法
第2步,确定排在第二个位置的同学;
第二位
B
C
A
C
A
B
第三位
C
B
C
A
B
A
每种情况均有2种选法
相应的排法
ACB
BAC
BCA
CAB
CBA
ABC
第3步,确定排在第三个位置的同学.
根据分步乘法计数原理,
不同的排法种数为:3×2×1=6 .
将3个不同元素,按照一定的顺序排成一列.
课程导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
北京、广州、南京、武汉4个城市相互通航,请列举出所有机票的情况,并指出 共有多少种机票.
确定要完成的一件事是什么?如何完成?
分步
第1步,确定作为起点的城市;共4种方法
起点
北京
广州
南京
第2步,确定作为终点的城市.每类有3种方法
终点
广州
根据分步乘法计数原理,
不同的排法种数为:4×3=12 .
南京
武汉
南京
武汉
北京
武汉
北京
广州
武汉
北京
广州
南京
从4个不同元素中,取出2个元素,并按照一定的顺序排成一列.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
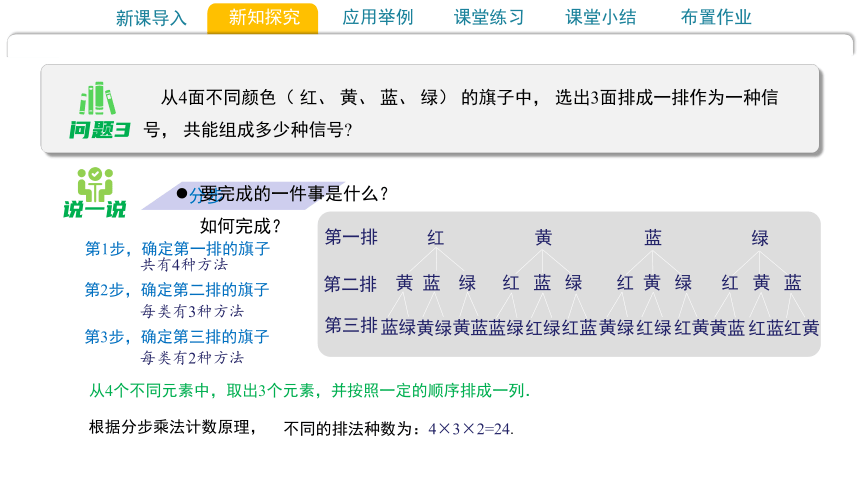
从4面不同颜色( 红、 黄、 蓝、 绿) 的旗子中, 选出3面排成一排作为一种信号, 共能组成多少种信号
根据分步乘法计数原理,
第1步,确定第一排的旗子
第2步,确定第二排的旗子
第3步,确定第三排的旗子
第二排
共有4种方法
每类有3种方法
每类有2种方法
不同的排法种数为:4×3×2=24.
第三排
黄 蓝 绿
红 蓝 绿
红 黄 绿
红 黄 蓝
蓝绿
黄绿
黄蓝
蓝绿
红绿
红蓝
黄绿
红绿
红黄
黄蓝
红蓝
红黄
分步
要完成的一件事是什么?如何完成?
第一排
红
黄
蓝
绿
从4个不同元素中,取出3个元素,并按照一定的顺序排成一列.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
在日常生活中,我们经常遇到下面一些问题,这些问题有什么共同特征呢?
(1) 3名同学排成一行照相,共有多少种排法?
(2)北京、广州、南京、武汉4个城市相互通航,请列举出所有机票的情况,
并指出共有多少种机票.
(3)从4面不同颜色(红、黄、蓝、绿)的旗子中, 选出3面排成一排作为一 种信号,共能组成多少种信号?
将3个不同元素,按照一定的顺序排成一列.
从4个不同元素中,取出2个元素,并按照一定的顺序排成一列.
从4个不同元素中,取出3个元素,并按照一定的顺序排成一列.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
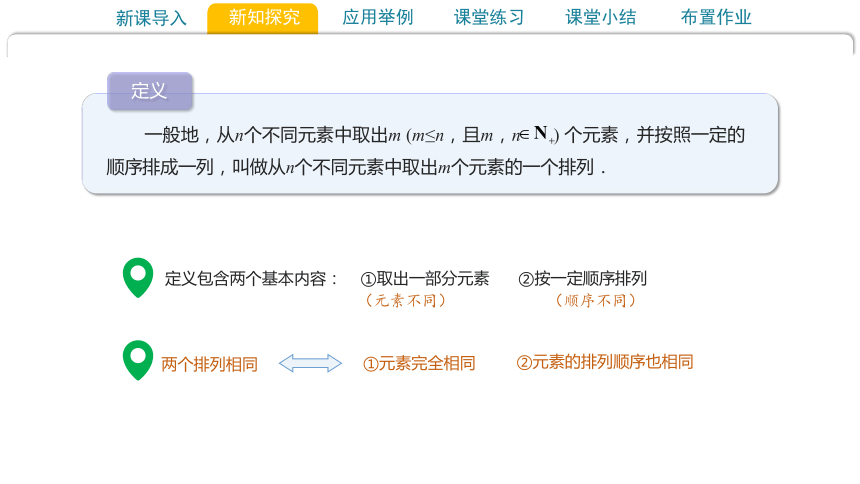
定义
一般地,从n个不同元素中取出m (m≤n,且m,n ) 个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
两个排列相同
①元素完全相同
②元素的排列顺序也相同
定义包含两个基本内容:
①取出一部分元素
(元素不同)
(顺序不同)
②按一定顺序排列
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
(1)10名学生中抽2名学生开会
(2)10名学生中选2名做正、副组长
(3)从2,3,5,7,11中任取两个数相乘
(4)从2,3,5,7,11中任取两个数相除
(5)从0-9中任取两个数组成一个集合
(6)从0-9中任取两个数组成一个点的坐标
(7)从圆上的10个点中任取两点为端点作弦
(8)从圆上的10个点中任取两点为起终点作向量
下列问题中哪些是排列问题?为什么?
无序
有序
无序
有序
无序
有序
无序
有序
对于每一种既定结果,改变其元素顺序,看是否会形成不同结果:
若是,则是排列;
若否,则不是排列.
如何判断一个问题是否是排列问题?
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
定义
我们把从n个不同元素中取出m (m≤n,且m,n ) 个元素的所有不同排列的个数,叫作从n个不同元素中取出m个元素的排列数,记作 .
你能用排列数来表示问题(1),(2),(3)的结论吗
北京、广州、南京、武汉4个城市相互通航,所有机票的种数,
是从4个元素中任取2个进行排列;
从4面不同颜色的旗子中,选出3面排成一排作为一种信号,总的
信号数量,是从4个元素中任取3个进行排列.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
从n个不同元素中取出2个元素的排列数 是多少?
对3个元素进行排列:
从4个元素中任取2个进行排列:
从4个元素中任取3个进行排列:
位置1
位置2
n
n-1
第1步,确定位置1上的数字
共有n种方法
第2步,确定位置2上的数字
共有n-1种方法
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
(1)请列出从5个不同元素中取出2个元素的所有排列,并计算 .
(2)计算排列数 .
是否是排列问题?
从5个不同元素中取出2个元素进行排序
位置1
位置2
5
4
解:(1)设5个不同元素分别为a,b,c,d,e.
按分步乘法计数原理:
第1步,确定位置1上的数字
共有5种方法
第2步,确定位置2上的数字
共有4种方法
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
(1)请列出从5个不同元素中取出2个元素的所有排列,并计算 .
(2)计算排列数 .
从n个不同元素中取出3个元素进行排序
位置1
位置2
n
n-1
解:(2)根据分步乘法计数原理,
第1步,确定位置1上的数字
共有n种方法
第2步,确定位置2上的数字
共有n-2种方法
第3步,确定位置3上的数字
共有n-1种方法
位置3
n-2
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
从甲、乙、丙三人中选出两人并站成一排的所有站法为( )
A.甲乙,乙甲,甲丙,丙甲 B.甲乙丙,乙丙甲
C.甲乙,甲丙,乙甲,乙丙,丙甲,丙乙 D.甲乙,甲丙,乙丙
从3个不同元素中取出2个元素进行排序
解:选择甲乙:甲乙,乙甲;
选择甲丙:甲丙,丙甲;
选择乙丙:乙丙,丙乙,
C
从甲、乙、丙三人中选出两人并站成一排的所有站法为:甲乙,乙甲,甲丙,丙甲,乙丙,丙乙,
故选C.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
(多选题)下面问题中,不是排列问题的是( )
A.由1,2,3三个数字组成无重复数字的三位数
B.从40人中选5人组成篮球队
C.从100人中选2人抽样调查
D.从1,2,3,4,5中选2个数组成集合
解:
BCD
选项A中组成的三位数与数字的排列顺序有关,选项B,C,D只需取出元素即可,与元素的排列顺序无关.
故选BCD.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
元旦来临之际,某寝室四位同学各有一张贺年卡,并且要送给该寝室的其中一位同学,但每人都必须得到一张,则不同的送法有___种.
解:将4张贺卡分别记为A,B,C,D,按题意进行排列,用树状图表示为:
由此可知共有9种送法.
B
A
C
D
D
D
A
C
D
D
A
B
A
D
C
A
C
B
B
A
D
C
C
A
B
A
B
C
B
A
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
京沪高速铁路自北京南站至上海虹桥站,双线铁路全长1318公里,途经北京、天津、河北、山东、安徽、江苏、上海7个省市,设立包括北京南、天津西、济南西、南京南、苏州北、上海虹桥等在内的21个车站,计算铁路部门要为这21个车站准备多少种不同的高铁票?
解:对于两个高铁站A和B,从A到B的高铁票与从B到A的高铁票不同,
因为每张票对应一个起点站和一个终点站,因此,准备的高铁票的种数应为从21个不同元素中,每次取出2个不同元素的排列的个数,为 .
所以一共需要为这21个车站准备420种不同的高铁票.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
排列是分步乘法计数原理的重要应用,其特征如下:
一是“取出元素”,
二是“按照一定的顺序进行排列”.“一定的顺序"与位置有关,这也是判断一个问题是不是排列问题的重要标志.
根据排列的定义,两个排列相同,当且仅当两个排列的元素完全相同,而且元素的排列顺序也相同.
我们还了解了排列数的定义,学会计算引例中的排列数.
课堂小结
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
计数原理
分类:
分步:
排列
排列数
公式
计数原理与排列
概念:从n个不同元素中取出m(m≤n,且m,n )个元素,并按 照一定的顺序排成一列.
定义: n个不同元素中取出m (m≤n,且m,n ) 个元素的
所有不同排列的个数.
完成一件事有不同方案.
完成一件事分成几个步骤.
结构框图
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
教材第162页练习第1,2题.
分类加法计数原理
…
m1
m2
mn
N=m1+m2+…+mn
分步乘法计数原理
……
m1
m2
mn
N=m1m2·…·mn
A
B
A
B
课程导入入
新知探究
应用举例
课堂练习
课堂小结
布置作业
在日常生活中,我们经常遇到下面一些问题,这些问题有什么共同特征呢?
(1)3名同学排成一行照相,共有多少种排法?
(2)北京、广州、南京、武汉4个城市相互通航,请列举出所有机票的情况,
并指出共有多少种机票.
(3)从4面不同颜色(红、黄、蓝、绿)的旗子中, 选出3面排成一排作为一 种信号,共能组成多少种信号?
课程导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
3名同学排成一行照相,共有多少种排法?
确定要完成的一件事是什么?
怎样完成这件事?分类 or 分步?
分步
第1步,确定排在第一个位置的同学;
A、B、C
第一位
A
B
C
3种选法
第2步,确定排在第二个位置的同学;
第二位
B
C
A
C
A
B
第三位
C
B
C
A
B
A
每种情况均有2种选法
相应的排法
ACB
BAC
BCA
CAB
CBA
ABC
第3步,确定排在第三个位置的同学.
根据分步乘法计数原理,
不同的排法种数为:3×2×1=6 .
将3个不同元素,按照一定的顺序排成一列.
课程导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
北京、广州、南京、武汉4个城市相互通航,请列举出所有机票的情况,并指出 共有多少种机票.
确定要完成的一件事是什么?如何完成?
分步
第1步,确定作为起点的城市;共4种方法
起点
北京
广州
南京
第2步,确定作为终点的城市.每类有3种方法
终点
广州
根据分步乘法计数原理,
不同的排法种数为:4×3=12 .
南京
武汉
南京
武汉
北京
武汉
北京
广州
武汉
北京
广州
南京
从4个不同元素中,取出2个元素,并按照一定的顺序排成一列.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
从4面不同颜色( 红、 黄、 蓝、 绿) 的旗子中, 选出3面排成一排作为一种信号, 共能组成多少种信号
根据分步乘法计数原理,
第1步,确定第一排的旗子
第2步,确定第二排的旗子
第3步,确定第三排的旗子
第二排
共有4种方法
每类有3种方法
每类有2种方法
不同的排法种数为:4×3×2=24.
第三排
黄 蓝 绿
红 蓝 绿
红 黄 绿
红 黄 蓝
蓝绿
黄绿
黄蓝
蓝绿
红绿
红蓝
黄绿
红绿
红黄
黄蓝
红蓝
红黄
分步
要完成的一件事是什么?如何完成?
第一排
红
黄
蓝
绿
从4个不同元素中,取出3个元素,并按照一定的顺序排成一列.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
在日常生活中,我们经常遇到下面一些问题,这些问题有什么共同特征呢?
(1) 3名同学排成一行照相,共有多少种排法?
(2)北京、广州、南京、武汉4个城市相互通航,请列举出所有机票的情况,
并指出共有多少种机票.
(3)从4面不同颜色(红、黄、蓝、绿)的旗子中, 选出3面排成一排作为一 种信号,共能组成多少种信号?
将3个不同元素,按照一定的顺序排成一列.
从4个不同元素中,取出2个元素,并按照一定的顺序排成一列.
从4个不同元素中,取出3个元素,并按照一定的顺序排成一列.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
定义
一般地,从n个不同元素中取出m (m≤n,且m,n ) 个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
两个排列相同
①元素完全相同
②元素的排列顺序也相同
定义包含两个基本内容:
①取出一部分元素
(元素不同)
(顺序不同)
②按一定顺序排列
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
(1)10名学生中抽2名学生开会
(2)10名学生中选2名做正、副组长
(3)从2,3,5,7,11中任取两个数相乘
(4)从2,3,5,7,11中任取两个数相除
(5)从0-9中任取两个数组成一个集合
(6)从0-9中任取两个数组成一个点的坐标
(7)从圆上的10个点中任取两点为端点作弦
(8)从圆上的10个点中任取两点为起终点作向量
下列问题中哪些是排列问题?为什么?
无序
有序
无序
有序
无序
有序
无序
有序
对于每一种既定结果,改变其元素顺序,看是否会形成不同结果:
若是,则是排列;
若否,则不是排列.
如何判断一个问题是否是排列问题?
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
定义
我们把从n个不同元素中取出m (m≤n,且m,n ) 个元素的所有不同排列的个数,叫作从n个不同元素中取出m个元素的排列数,记作 .
你能用排列数来表示问题(1),(2),(3)的结论吗
北京、广州、南京、武汉4个城市相互通航,所有机票的种数,
是从4个元素中任取2个进行排列;
从4面不同颜色的旗子中,选出3面排成一排作为一种信号,总的
信号数量,是从4个元素中任取3个进行排列.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
从n个不同元素中取出2个元素的排列数 是多少?
对3个元素进行排列:
从4个元素中任取2个进行排列:
从4个元素中任取3个进行排列:
位置1
位置2
n
n-1
第1步,确定位置1上的数字
共有n种方法
第2步,确定位置2上的数字
共有n-1种方法
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
(1)请列出从5个不同元素中取出2个元素的所有排列,并计算 .
(2)计算排列数 .
是否是排列问题?
从5个不同元素中取出2个元素进行排序
位置1
位置2
5
4
解:(1)设5个不同元素分别为a,b,c,d,e.
按分步乘法计数原理:
第1步,确定位置1上的数字
共有5种方法
第2步,确定位置2上的数字
共有4种方法
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
(1)请列出从5个不同元素中取出2个元素的所有排列,并计算 .
(2)计算排列数 .
从n个不同元素中取出3个元素进行排序
位置1
位置2
n
n-1
解:(2)根据分步乘法计数原理,
第1步,确定位置1上的数字
共有n种方法
第2步,确定位置2上的数字
共有n-2种方法
第3步,确定位置3上的数字
共有n-1种方法
位置3
n-2
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
从甲、乙、丙三人中选出两人并站成一排的所有站法为( )
A.甲乙,乙甲,甲丙,丙甲 B.甲乙丙,乙丙甲
C.甲乙,甲丙,乙甲,乙丙,丙甲,丙乙 D.甲乙,甲丙,乙丙
从3个不同元素中取出2个元素进行排序
解:选择甲乙:甲乙,乙甲;
选择甲丙:甲丙,丙甲;
选择乙丙:乙丙,丙乙,
C
从甲、乙、丙三人中选出两人并站成一排的所有站法为:甲乙,乙甲,甲丙,丙甲,乙丙,丙乙,
故选C.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
(多选题)下面问题中,不是排列问题的是( )
A.由1,2,3三个数字组成无重复数字的三位数
B.从40人中选5人组成篮球队
C.从100人中选2人抽样调查
D.从1,2,3,4,5中选2个数组成集合
解:
BCD
选项A中组成的三位数与数字的排列顺序有关,选项B,C,D只需取出元素即可,与元素的排列顺序无关.
故选BCD.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
元旦来临之际,某寝室四位同学各有一张贺年卡,并且要送给该寝室的其中一位同学,但每人都必须得到一张,则不同的送法有___种.
解:将4张贺卡分别记为A,B,C,D,按题意进行排列,用树状图表示为:
由此可知共有9种送法.
B
A
C
D
D
D
A
C
D
D
A
B
A
D
C
A
C
B
B
A
D
C
C
A
B
A
B
C
B
A
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
京沪高速铁路自北京南站至上海虹桥站,双线铁路全长1318公里,途经北京、天津、河北、山东、安徽、江苏、上海7个省市,设立包括北京南、天津西、济南西、南京南、苏州北、上海虹桥等在内的21个车站,计算铁路部门要为这21个车站准备多少种不同的高铁票?
解:对于两个高铁站A和B,从A到B的高铁票与从B到A的高铁票不同,
因为每张票对应一个起点站和一个终点站,因此,准备的高铁票的种数应为从21个不同元素中,每次取出2个不同元素的排列的个数,为 .
所以一共需要为这21个车站准备420种不同的高铁票.
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
排列是分步乘法计数原理的重要应用,其特征如下:
一是“取出元素”,
二是“按照一定的顺序进行排列”.“一定的顺序"与位置有关,这也是判断一个问题是不是排列问题的重要标志.
根据排列的定义,两个排列相同,当且仅当两个排列的元素完全相同,而且元素的排列顺序也相同.
我们还了解了排列数的定义,学会计算引例中的排列数.
课堂小结
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
计数原理
分类:
分步:
排列
排列数
公式
计数原理与排列
概念:从n个不同元素中取出m(m≤n,且m,n )个元素,并按 照一定的顺序排成一列.
定义: n个不同元素中取出m (m≤n,且m,n ) 个元素的
所有不同排列的个数.
完成一件事有不同方案.
完成一件事分成几个步骤.
结构框图
新课导入
新知探究
应用举例
课堂练习
课堂小结
布置作业
教材第162页练习第1,2题.
同课章节目录
