北师大版高中数学选择性必修第一册 5.4第1课时二项式定理的推导 课件(共19张PPT)
文档属性
| 名称 | 北师大版高中数学选择性必修第一册 5.4第1课时二项式定理的推导 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 505.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 11:13:59 | ||
图片预览






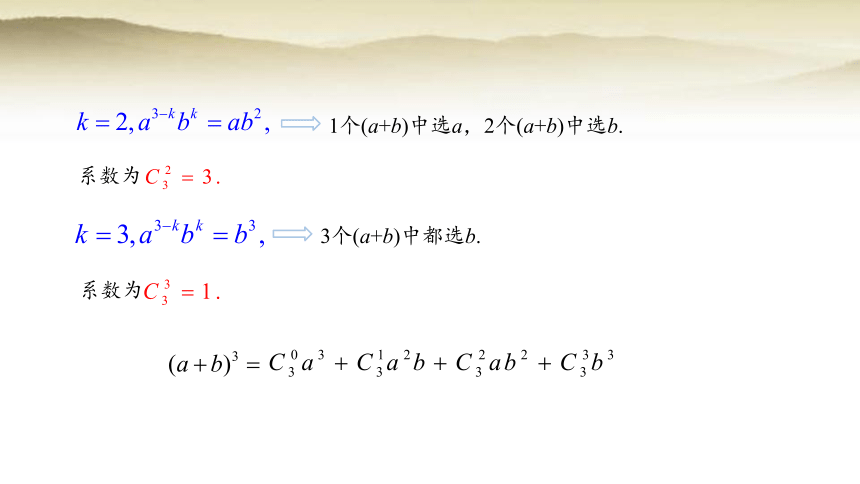
文档简介
(共19张PPT)
5.4 第1课时
新授课
二项式定理的推导
根据多项式的乘法法则,容易知道(a+b)2=a2+2ab+b2,
(a+b)3=a3+3a2b+3ab2+b3,如果称等式的右边为左边的展开式,那么如何求出(a+b)n的展开式?
1.能用多项式法则和计数原理推导出二项式定理.
2.会用二项式定理解决与二项展开式有关的简单问题.
请计算(a+b)2,(a+b)3和(a+b)4,分析其运算过程,并用组合数表示各项系数.
知识点一:二项式定理
根据多项式乘法法则,
项的形式:
展开式共有:
当 时,
2个(a+b)都不选b.
a2的系数为 ,即a2系数为1;
3项
当 时,
当 时,
1个(a+b)中选a,另一个(a+b)中选b.
2个(a+b)都选b.
ab的系数为 ,即ab系数为2;
b2的系数为 ,即b2系数为1.
展开式共有:
项的形式:
系数为
系数为
4项
3个(a+b)都选a.
2个(a+b)中选a,1个(a+b)中选b.
系数为
系数为
1个(a+b)中选a,2个(a+b)中选b.
3个(a+b)中都选b.
a4
a3b
ab3
b4
a2b2
问题:根据以上分析,猜想(a+b)n的展开式是怎样的?
各项是从n个因式中各取一个字母相乘得到关于a,b的n次单项式,有
项的形式:
展开式共有:
n+1项.
从n个因式中都取b,系数为
从n个因式中取k个b,系数为
从n个因式中取2个b,系数为
从n个因式中取1个b,系数为
从n个因式中都不取b,系数为
项的系数:
……
……
二项式定理:
(a+b)n的二项展开式
上式可简写成
二项式系数
概念生成
式中的 用Tk+1表示,称为二项展开式中第(k+1)项,又称为二项式通项, 记作
二项式定理:
知识点二:二项式定理的应用
例1 求 的展开式.
解:根据二项式定理,
例2 求 的展开式.
解:根据二项式定理,
例3 求 的展开式.
解:根据二项式定理,
例4 求 的展开式中x4y3的系数.
解:设展开式中的第k+1项为含x4y3的项,
令7-k=4,得k=3,
则
∴x4y3的系数为
求二项展开式的特定项的系数的一般步骤:
归纳总结
1.写出通项公式,其所有的字母的指数恰好都是题目要求的项;
2.合并通项公式中同一字母的指数;
3.根据具体要求,令字母的指数符合题目要求;
4.再计算求得二项展开式的特定项的系数.
求 的展开式中x3的系数.
练一练
解:设展开式中的第k+1项为含x3的项,
令9-2k=3,得k=3,
则
∴x3的系数为
根据今天所学,回答下列问题:
1.二项式定理是怎样推导的?
2.二项式系数和展开式通项分别是什么?
5.4 第1课时
新授课
二项式定理的推导
根据多项式的乘法法则,容易知道(a+b)2=a2+2ab+b2,
(a+b)3=a3+3a2b+3ab2+b3,如果称等式的右边为左边的展开式,那么如何求出(a+b)n的展开式?
1.能用多项式法则和计数原理推导出二项式定理.
2.会用二项式定理解决与二项展开式有关的简单问题.
请计算(a+b)2,(a+b)3和(a+b)4,分析其运算过程,并用组合数表示各项系数.
知识点一:二项式定理
根据多项式乘法法则,
项的形式:
展开式共有:
当 时,
2个(a+b)都不选b.
a2的系数为 ,即a2系数为1;
3项
当 时,
当 时,
1个(a+b)中选a,另一个(a+b)中选b.
2个(a+b)都选b.
ab的系数为 ,即ab系数为2;
b2的系数为 ,即b2系数为1.
展开式共有:
项的形式:
系数为
系数为
4项
3个(a+b)都选a.
2个(a+b)中选a,1个(a+b)中选b.
系数为
系数为
1个(a+b)中选a,2个(a+b)中选b.
3个(a+b)中都选b.
a4
a3b
ab3
b4
a2b2
问题:根据以上分析,猜想(a+b)n的展开式是怎样的?
各项是从n个因式中各取一个字母相乘得到关于a,b的n次单项式,有
项的形式:
展开式共有:
n+1项.
从n个因式中都取b,系数为
从n个因式中取k个b,系数为
从n个因式中取2个b,系数为
从n个因式中取1个b,系数为
从n个因式中都不取b,系数为
项的系数:
……
……
二项式定理:
(a+b)n的二项展开式
上式可简写成
二项式系数
概念生成
式中的 用Tk+1表示,称为二项展开式中第(k+1)项,又称为二项式通项, 记作
二项式定理:
知识点二:二项式定理的应用
例1 求 的展开式.
解:根据二项式定理,
例2 求 的展开式.
解:根据二项式定理,
例3 求 的展开式.
解:根据二项式定理,
例4 求 的展开式中x4y3的系数.
解:设展开式中的第k+1项为含x4y3的项,
令7-k=4,得k=3,
则
∴x4y3的系数为
求二项展开式的特定项的系数的一般步骤:
归纳总结
1.写出通项公式,其所有的字母的指数恰好都是题目要求的项;
2.合并通项公式中同一字母的指数;
3.根据具体要求,令字母的指数符合题目要求;
4.再计算求得二项展开式的特定项的系数.
求 的展开式中x3的系数.
练一练
解:设展开式中的第k+1项为含x3的项,
令9-2k=3,得k=3,
则
∴x3的系数为
根据今天所学,回答下列问题:
1.二项式定理是怎样推导的?
2.二项式系数和展开式通项分别是什么?
同课章节目录
