北师大版高中数学选择性必修第一册 4.1数学建模实例 课件(共18张PPT)
文档属性
| 名称 | 北师大版高中数学选择性必修第一册 4.1数学建模实例 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 29.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 11:14:33 | ||
图片预览





文档简介
(共18张PPT)
十字路口汽车通行问题
数学建模实例
课前准备
(1)分组:5人一组,其中三人分别负责数学、物理和计算机领域的问题;一人为组长,负责组织协调;还有一人为发言人,负责整合成果交流展示.
(2)让学生前一天观察学校门口的那个十字路口一次绿灯时长是多少?一次绿灯时长一条直行道路上能通过多少辆车呢?
(3)实际测量、调查或上网查阅小轿车车长、十字路口等候车距、十字路口限速、车起步反应时间、车起步加速度,并设计数据收集表,完成数据收集.
提出问题
随着城市经济的不断发展,工业化的进步,居民生活水平不断提高,汽车数量也在增加,我国城市交通拥堵问题日益严重.根据生活经验,红绿灯路口是交通拥堵的多发地点.
问题:对于拥堵现象,如何提高绿灯的通行效率?
提出问题
在一个十字路口, 每次亮绿灯时间长为15s, 那么, 每次亮绿灯时, 在一条直行道路上能有多少汽车通过十字路口
建立模型
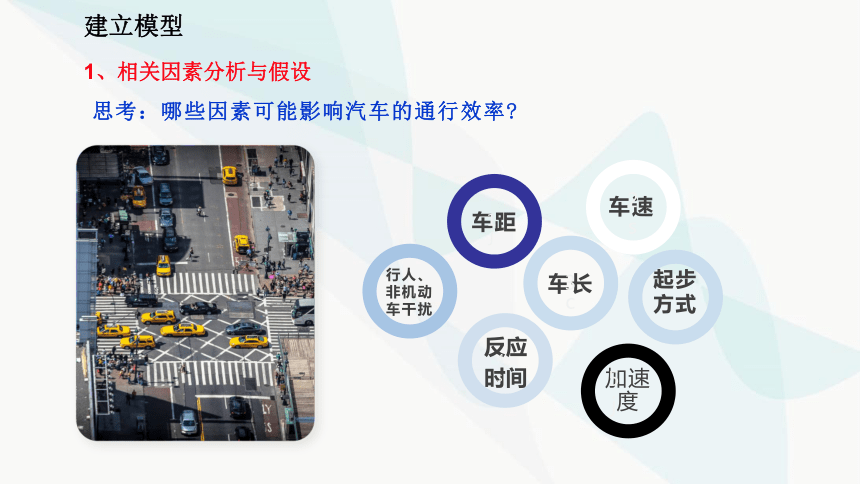
思考:哪些因素可能影响汽车的通行效率
行人、非机动车干扰
车距
车速
反应时间
加速度
车长
起步方式
1 j
2
s
3c
4s
5
j
1、相关因素分析与假设
原则: 有利于建立模型, 基本符合实际情况
相关因素 假设 变量
车长不同 车辆长度都相等 l 5m
车距不同 相邻两辆车的车距都相等 d 2m
起步方式 汽车都是在静止状态下匀加速启动 a 2m/s2
是否限速 是 v* 40km/h
反应时间不同 前后车辆启动的延时时间相等 T 1s
行人、非机动车干扰 不会发生堵塞
抓住主要 忽略次要
建立模型
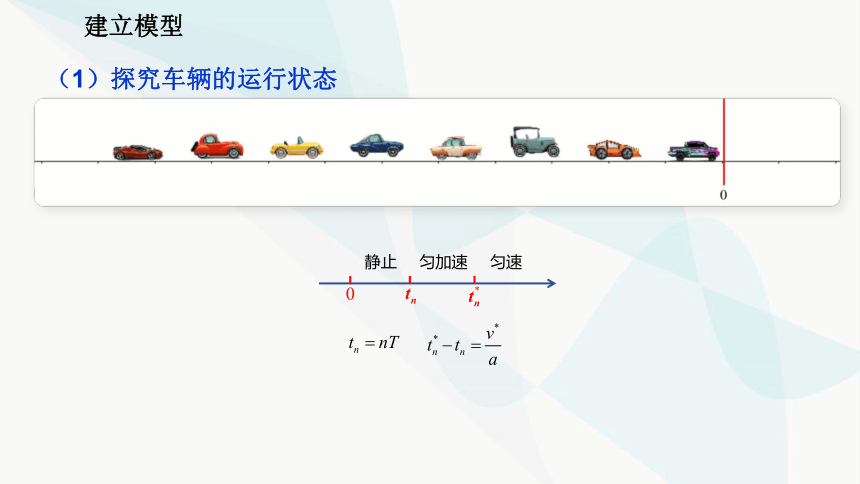
(1)探究车辆的运行状态
静止
匀加速
匀速
建立模型
0
(2)探究第n辆车的初始位置的表达式
假设第一辆汽车车头的初始位置恰好对齐停车线,将停车线位置记作0,则
为首项是 ,公差为 的等差数列
建立模型
(3)探究第n辆车在 t 时刻的位置
建立模型
求解模型
汽车序号n 1 2 3 4 5 6 7 8
Sn(15) 124.6 106.5 88.4 70.3 52.2 34.1 16.0 -2.1
检验模型
在视频中,一个十字路口,在绿灯亮的期间,一条直行道路只通过了5辆汽车. 这说明该模型有漏洞.请讨论模型中的哪个数据不太符合实际呢?
调整模型
检验结果
十字路口,一条直行道路上只有5汽车通过,与实际情况非常接近.
调整“反应时间”为2 s,验证结果
评价模型
探究:你认为哪个量对车辆通行效率影响最大?
1) 车距缩短1倍
2) 加速度提高1倍
3) 限速提高1倍
4) 反应时间缩短1倍
评价方案:通过改变变量的取值,评价变量对车辆通行效率的影响。
评价模型
探究:你认为哪个量对车辆通行效率影响最大?
探究一 “车距”调整为“1”
探究二 “加速度”调整为“4”
汽车通行效率没有提升很多,并且缩短车距存在危险,不可取.
汽车通行效率没有提升,并且提升加速度,对汽车性能要求很高.
评价模型
探究:你认为哪个量对车辆通行效率影响最大?
探究三 “限速”调整为“80”
探究四 将“反应时间”调整为“0.5”
汽车通行效率没有提升,并且十字路口限速,有危险.
反应时间对通行效率提升有很大影响.
交通大建言
问题1:如果反应时间为0,会怎样?
问题2:你能提出什么建议提升十字路口车辆通行效率呢?
评价模型
课堂总结
问题:1.本节课学习了什么知识?
2.本节课体现了哪些核心素养?
数学建模的一般步骤
直观想象、逻辑推理、数学抽象
课后作业
【实践操作】选择你熟悉的十字路口,具体调查它的通行能力,采用本节所学尝试数学建模.
【理论提升】在互联网上搜索一篇数学建模论文,分析步骤,审视假设的合理性.
十字路口汽车通行问题
数学建模实例
课前准备
(1)分组:5人一组,其中三人分别负责数学、物理和计算机领域的问题;一人为组长,负责组织协调;还有一人为发言人,负责整合成果交流展示.
(2)让学生前一天观察学校门口的那个十字路口一次绿灯时长是多少?一次绿灯时长一条直行道路上能通过多少辆车呢?
(3)实际测量、调查或上网查阅小轿车车长、十字路口等候车距、十字路口限速、车起步反应时间、车起步加速度,并设计数据收集表,完成数据收集.
提出问题
随着城市经济的不断发展,工业化的进步,居民生活水平不断提高,汽车数量也在增加,我国城市交通拥堵问题日益严重.根据生活经验,红绿灯路口是交通拥堵的多发地点.
问题:对于拥堵现象,如何提高绿灯的通行效率?
提出问题
在一个十字路口, 每次亮绿灯时间长为15s, 那么, 每次亮绿灯时, 在一条直行道路上能有多少汽车通过十字路口
建立模型
思考:哪些因素可能影响汽车的通行效率
行人、非机动车干扰
车距
车速
反应时间
加速度
车长
起步方式
1 j
2
s
3c
4s
5
j
1、相关因素分析与假设
原则: 有利于建立模型, 基本符合实际情况
相关因素 假设 变量
车长不同 车辆长度都相等 l 5m
车距不同 相邻两辆车的车距都相等 d 2m
起步方式 汽车都是在静止状态下匀加速启动 a 2m/s2
是否限速 是 v* 40km/h
反应时间不同 前后车辆启动的延时时间相等 T 1s
行人、非机动车干扰 不会发生堵塞
抓住主要 忽略次要
建立模型
(1)探究车辆的运行状态
静止
匀加速
匀速
建立模型
0
(2)探究第n辆车的初始位置的表达式
假设第一辆汽车车头的初始位置恰好对齐停车线,将停车线位置记作0,则
为首项是 ,公差为 的等差数列
建立模型
(3)探究第n辆车在 t 时刻的位置
建立模型
求解模型
汽车序号n 1 2 3 4 5 6 7 8
Sn(15) 124.6 106.5 88.4 70.3 52.2 34.1 16.0 -2.1
检验模型
在视频中,一个十字路口,在绿灯亮的期间,一条直行道路只通过了5辆汽车. 这说明该模型有漏洞.请讨论模型中的哪个数据不太符合实际呢?
调整模型
检验结果
十字路口,一条直行道路上只有5汽车通过,与实际情况非常接近.
调整“反应时间”为2 s,验证结果
评价模型
探究:你认为哪个量对车辆通行效率影响最大?
1) 车距缩短1倍
2) 加速度提高1倍
3) 限速提高1倍
4) 反应时间缩短1倍
评价方案:通过改变变量的取值,评价变量对车辆通行效率的影响。
评价模型
探究:你认为哪个量对车辆通行效率影响最大?
探究一 “车距”调整为“1”
探究二 “加速度”调整为“4”
汽车通行效率没有提升很多,并且缩短车距存在危险,不可取.
汽车通行效率没有提升,并且提升加速度,对汽车性能要求很高.
评价模型
探究:你认为哪个量对车辆通行效率影响最大?
探究三 “限速”调整为“80”
探究四 将“反应时间”调整为“0.5”
汽车通行效率没有提升,并且十字路口限速,有危险.
反应时间对通行效率提升有很大影响.
交通大建言
问题1:如果反应时间为0,会怎样?
问题2:你能提出什么建议提升十字路口车辆通行效率呢?
评价模型
课堂总结
问题:1.本节课学习了什么知识?
2.本节课体现了哪些核心素养?
数学建模的一般步骤
直观想象、逻辑推理、数学抽象
课后作业
【实践操作】选择你熟悉的十字路口,具体调查它的通行能力,采用本节所学尝试数学建模.
【理论提升】在互联网上搜索一篇数学建模论文,分析步骤,审视假设的合理性.
同课章节目录
