浙江省2025届九年级下学期中考模拟(六)数学试卷(含答案)
文档属性
| 名称 | 浙江省2025届九年级下学期中考模拟(六)数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 163.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 14:47:05 | ||
图片预览




文档简介
2025年浙江省中考数学模拟试卷(六)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.以下四个城市中某天上午9时气温最低的城市是( )
杭州 温州 宁波 嘉兴
-2℃ 0℃ 1℃ -1℃
A. 杭州 B. 温州 C. 宁波 D. 嘉兴
2.6个相同正方体搭成的几何体俯视图为( )
A.
B.
C.
D.
3.截止2025年4月9日,《哪吒之魔童闹海》全球票房(含预售及海外)已破15600000000元.其中数“15600000000”用科学记数法表示为( )
A. 15.6×109 B. 1.56×1010 C. 0.156×1011 D. 1.56×1011
4.下列计算正确的是( )
A. a2+a2=a4 B. a3 a2=a6 C. a6÷a2=a3 D. (a3)3=a9
5.一次空气污染指数抽查中,收集到某地一周的数据如下:67,68,63,90,89,75,89.该组数据的中位数是( )
A. 68 B. 75 C. 89 D. 90
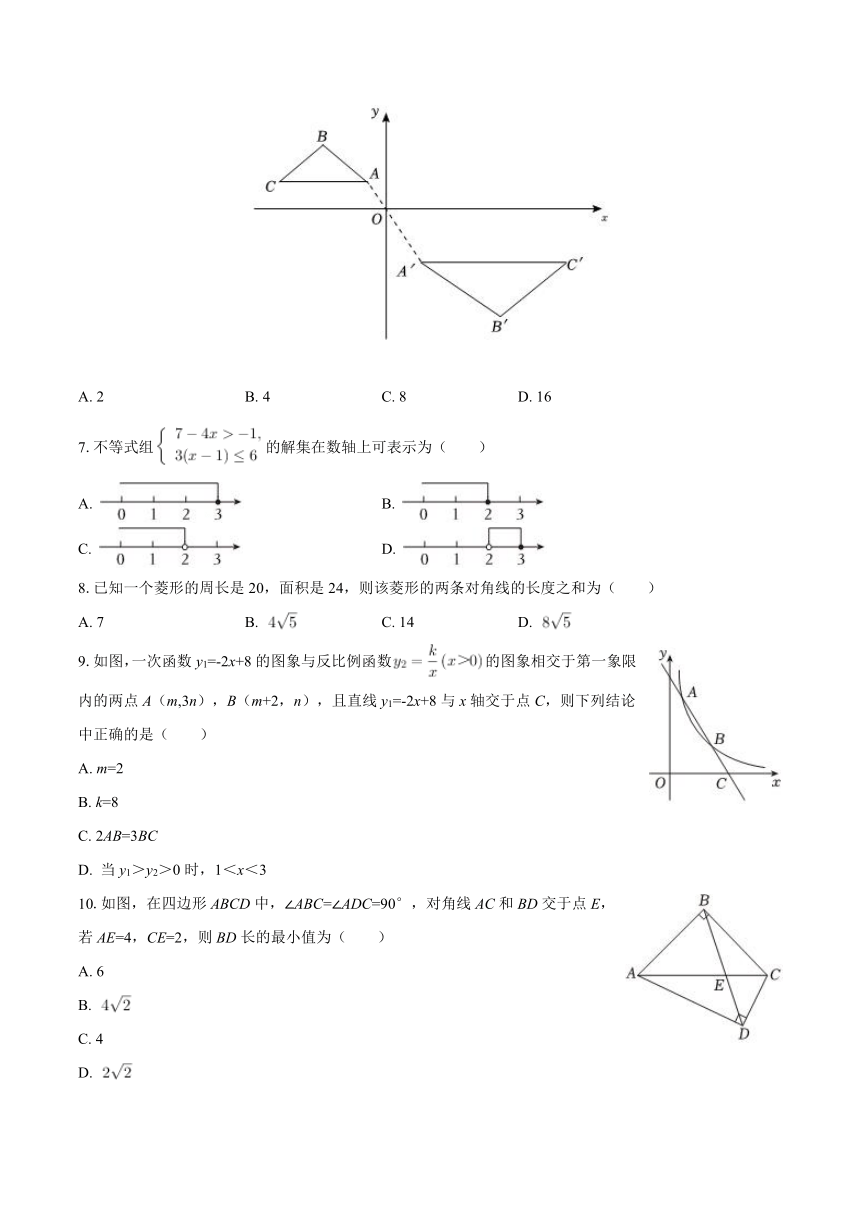
6.如图,在平面直角坐标系xOy中,△ABC和△A'B'C'位似,位似中心为原点O.已知点A(-1,1.5),点A′(2,-3),若△ABC的面积为2,则△A'B'C'的面积是( )
A. 2 B. 4 C. 8 D. 16
7.不等式组的解集在数轴上可表示为( )
A. B.
C. D.
8.已知一个菱形的周长是20,面积是24,则该菱形的两条对角线的长度之和为( )
A. 7 B. C. 14 D.
9.如图,一次函数y1=-2x+8的图象与反比例函数的图象相交于第一象限内的两点A(m,3n),B(m+2,n),且直线y1=-2x+8与x轴交于点C,则下列结论中正确的是( )
A. m=2
B. k=8
C. 2AB=3BC
D. 当y1>y2>0时,1<x<3
10.如图,在四边形ABCD中,∠ABC=∠ADC=90°,对角线AC和BD交于点E,若AE=4,CE=2,则BD长的最小值为( )
A. 6
B.
C. 4
D.
二、填空题:本题共6小题,每小题3分,共18分。
11.分解因式:x2-4x= .
12.一个不透明的袋子中,有5个除颜色外完全相同的小球,其中3个红球,2个白球.随机摸出一个小球,摸出红球的概率是______.
13.已知分式,若当x=1时分式的值为0,则实数a的值为______.
14.如图,AB是半圆O的直径,点C在半圆上,CD是半圆的切线,cosD=,∠CAB=30°,若CD=6,则AC的长是______.
15.“化积为方”是一个古老的几何学问题,即给定一个长方形,作一个和它面积相等的正方形,这也是证明勾股定理的一种思想方法.如图所示,在矩形ABCD中(AB>AD),以AD为边作正方形ADEF,在FE的延长线上取一点G,使得∠DGC=Rt∠,过点D作DH⊥DG交AB于点H,过点H作HK⊥GC于点K.若AF=2,BF=3FH,则FH的长为______.
16.已知二次函数y=ax2+2ax+c(a<0)的图象上有两点A(x1,y1),B(1,y2),当m-1≤x1≤m时,始终有y1<y2,则m的取值范围是______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
(1)计算:;
(2)解方程:x2+2x=8.
18.(本小题8分)
佳佳计算分式方程的过程如下:
解方程:
去分母,得1-x=-1-2………………………第①步
移项,得-x=-1-2+1…………………………第②步
合并同类项,得-x=-2…………………………第③步
系数化1,得x=2…………………………第④步
经检验,x=2是该分式方程的解.
(1)佳佳在计算过程中,第一次出现错误的步骤是______(填序号);
(2)请你写出正确的解答过程.
19.(本小题8分)
如图,平行四边形ABCD中,AE平分∠BAD交BC于点E.
(1)尺规作图:作CF平分∠BCD交AD于点F(不写作法,保留作图痕迹);
(2)求证:四边形AECF是平行四边形.
20.(本小题8分)
观察下面的等式:
第1个等式:,
第2个等式:,
第3个等式:,
第4个等式:,
……
按照以上规律,解决下列问题:
(1)写出第5个等式:______;
(2)请你猜想第n个等式(用含n的式子表示),并证明.
21.(本小题8分)
某校组织九年级学生参加研学活动,为了确定本次研学的目的地,学校对学生去向意愿进行了摸底调查(A:农家乐;B:科技馆;C:大学城).下面两幅统计图反映了抽取的部分学生对研学活动去向意愿的情况,请你根据图中的信息回答下列问题:
(1)本次调查抽取的学生总人数为______人,并补全条形统计图;
(2)求扇形统计图中选项B所对应的圆心角度数;
(3)若该校九年级的总人数为250人,试估计选择去大学城研学的总人数.
22.(本小题10分)
综合与实践:
背景:当前排球渐渐走入初中生的学习和生活中,排球运动不仅能提升身体素质,还能促进心理健康,对青少年的身心发展有着诸多益处.
排球的购买与售卖
素材1:为了能让学生日常锻炼“排球垫球”体育运动,某中学打算购进一批排球,计划购买甲品牌的排球35个,乙品牌的排球50个,共花费3550元.已知购买一个甲品牌的排球比购买一个乙品牌的排球少花20元.
素材2:某商店售卖丙品牌排球,进价为每个20元,当前售价为每个36元,每周可售出50个.经市场调查发现,售价每降低3元,每周可多售出15个.
任务1:求购买一个甲品牌、一个乙品牌的排球各需多少元?
任务2:求当一个丙品牌的排球售价为多少元时有最大利润?最大利润是多少?
23.(本小题10分)
在平面直角坐标系中,二次函数的表达式为y=mx2+(m+1)x+n,其中m-n=4.
(1)若此函数图象过点(2,5),求这个二次函数的表达式;
(2)若(x1,y1),(x2,y2)为此二次函数图象上不同的两个点,当x1=4-x2时,y1=y2,求m的值;
(3)若点(-1,t)在此二次函数图象上,当x≥-1时,y随x的增大而增大,求t的取值范围.
24.(本小题12分)
如图,点D是Rt△ABC斜边AB上的一点,以BD为直径的圆⊙O交边AC于E,F两点,连结DE,BE,BF,并且BE平分∠DBF.
(1)求证:△BCF∽△BED;
(2)若DE=2.5,CF=2,求BC的长;
(3)若BD=2AD,BF=8,求CF的长.
1.【答案】
解:由题意得:-2℃<-1℃<0℃<1℃,
∴四个城市中某天上午9时气温最低的城市是杭州.
故选:A.
2.【答案】
解:俯视图为.
故选:A.
3.【答案】
解:15600000000=1.56×1010.
故选:B.
4.【答案】
解:a2+a2=2a2,则A不符合题意;
a3 a2=a5,则B不符合题意;
a6÷a2=a4,则C不符合题意;
(a3)3=a9,则D符合题意;
故选:D.
5.【答案】
解:将这组数据重新排序为:63,67,68,75,89,89,90,则其中位数为75,
故选:B.
6.【答案】
解:∵△ABC和△A'B'C'位似,位似中心为原点O,点A(-1,1.5),点A′(2,-3),
∴△ABC与△A'B'C'的相似比为1:2,
∴△ABC与△A'B'C'的面积比为1:4,
∵△ABC的面积为2,
∴△A'B'C'的面积是8.
故选:C.
7.【答案】
解:,
解不等式①得,x<2,
解不等式②得,x≤3,
∴不等式组的解集为x<2.
∴不等式组的解集在数轴上表示,如图所示:
故选:C.
8.【答案】
解:如图所示:
∵四边形ABCD是菱形,
∴AO=CO=AC,DO=BO=BD,AC⊥BD,
∵菱形面积=BD AC=2OB OA=24,
∴OB OA=12①,
∵菱形的周长是20,
∴AB=5,
∵∠AOB=90°,
∴OB2+OA2=AB2=25②,
由①②两式可得49-2OD OA=25,
解得:OB+AO=7,
∴AC+BD=14,
故选:C.
9.【答案】
解:由条件可知,
解得,
故A选项不符合题意;
把n=2,m=1代入A(m,3n),B(m+2,n),得A(1,6),B(3,2),
则把A(1,6)代入,得,
∴k=6,
故B选项不符合题意;
∵直线y1=-2x+8与x轴交于点C,
∴令y1=0,则0=-2x+8,
解得x=4,
∴C(4,0),
∵A(1,6),B(3,2),
则,
,
则AB=2BC,
∴2AB=4BC,
故C选项不符合题意;
依题意,一次函数y1=-2x+8的图象与反比例函数的图象相交于第一象限内的两点A(1,6),B(3,2),
∴当y1>y2>0时,1<x<3,
故D选项符合题意;
故选:D.
10.【答案】
解:如图,∵∠ABC=∠ADC=90°,
∴A,B,C,D四点共圆,
∵AC为直径.
∴取AC的中点即圆心O,当弦BD⊥AC时,BD取到最小值.
∵AE=4,CE=2,
∴AC=6,
∴OB=OC=3,
∴OE=OC-CE=3-2=1,
在Rt△OEB 中,由勾股定理得,
,
∴,
即BD长的最小值为4,
故选:B.
11.【答案】
解:x2-4x=x(x-4).
故答案为:x(x-4).
12.【答案】
解:∵一个口袋里有5个除颜色外完全相同的小球,其中3个红球,2个白球,
∴摸到红球的概率是.
故答案为:.
13.【答案】
解:当x+a=0时分式值为0,
因为当x=1时分式的值为0,
所以1+a=0,
所以a=-1.
故答案为:-1.
14.【答案】
解:连接OC、BC,如图,
∵CD是半圆的切线,
∴OC⊥CD,
∴∠OCD=90°,
在Rt△OCD中,∵cosD==,
∴OD=CD=×6=10,
∴OC==8,
∵∠BOC=2∠BAC=60°,OC=OB,
∴△OCB为等边三角形,
∴BC=OC=8,
∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠BAC=30°,
∴AC=BC=8.
故答案为:8.
15.【答案】
解:∵DH⊥DG,HK⊥GC,
∴∠HDG=∠DGC=∠K=90°,
∴四边形DGKH是矩形,
∵四边形ABCD是矩形,四边形ADEF是正方形,
∴∠DAB=∠DAF=90°,∠ADC=∠ADE=90°,
∴点F在AB边上,点E在CD边上,
∵CD∥AB,
∴∠DEG=∠AFE=90°,
∴∠DEG=∠DAH,
在△DEG和△DAH中,
,
∴△DEG≌△DAH(ASA),
∴DG=DH,
∴四边形DGKH是正方形,
∴DH2=DH DG=2S△CDH,
∵AB=CD,
∴AB AD=CD AD=2S△CDH,
∴DH2=AB AD,
∴AD2+AH2=DH2=AB AD,
∵BF=3FH,
∴设FH=x,则BF=3x,
∵AF=AD=DE,
∴AH=AF-FH=2-x,AB=AF+BF=3x+2,
∴22+(2-x)2=DH2=2(3x+2),
∴4+4-4x+x2=6x+4,
∴x2-10x+4=0,
∴Δ=(-10)2-4×1×4=84,
∴,
则,或(不合题意,舍去),
解得,
故答案为:.
16.【答案】
解:二次函数的对称轴为直线,
∴当x1=-1×2-1=-3或x1=1时,y1=y2,
∵a<0,
∴抛物线的开口向下,
∴离对称轴越远函数值越小.
分类讨论:①x1<-3恒成立,则y1<y2,
∴m<-3;
②x1>1恒成立,则y1<y2.
∴m-1>1.即m>2.
综上所述.m的取值范围是m<-3或m>2.
故答案为:m<-3或m>2.
17.【答案】
(1)原式=;
(2)x2+2x=8,
x2+2x-8=0,
(x+4)(x-2)=0,
x+4=0或x-2=0,
解得:x1=-4,x2=2.
18.【答案】
(1),
去分母,得1-x=-1-2(x-3),
∴第一次出现错误的是①.
故答案为:①;
(2),
去分母,得1-x=-1-2(x-3),
去括号,得1-x=-1-2x+6,
移项,得-x+2x=-1+6-1,
合并同类项,得x=4,
经检验,x=4是该分式方程的解.
19.【答案】
(1)解:图形如图所示:
(2)证明:∵四边形ABC都是平行四边形,
∴∠BAC=∠DCB,AD∥BC,
∵AE,CF方便平分∠BAD,∠BCD,
∴∠DAE=∠ECF,
∵AD∥CB,
∴∠DAE=∠AEB=∠ECF,
∴AE∥CF,
∴四边形AECF是平行四边形.
20.【答案】
(1)第5个等式为:=(),
故答案为:=();
(2)第n个式子为=(-),
右边=(-)===左边,
∴=(-),
故答案为:=(-).
21.【答案】
(1)15÷30%=50(人),
∴本次调查抽取的学生总人数为50人,
故答案为:50;
去B科技馆的人数:50-15-25=10(人),
补全条形统计图:
(2)360°×=72°,
答:选项B所对应的圆心角度数为72°;
(3)250×=125(人),
答:估计选择去大学城研学的总人数125人.
22.【答案】
解:任务1:设购买一个甲品牌排球需x元,
依题意得:35x+50(x+20)=3550,
解得:x=30,
∴30+20=50(元),
答:购买一个甲品牌的排球需30元,购买一个乙品牌的排球需50元;
任务2:设当一个丙品牌的排球降价y元时,其利润为w元,
依题意,得:w=(36-20-y)(50+)
=(16-y)(50+5y)
=-5y2+30y+800$
=-5(y-3)2+845,
当y=3,即售价为36-3=33元时利润w有最大值,最大值为845.
答:当一个丙品牌的排球售价为33元时有最大利润,最大利润是845元.
23.【答案】
(1)由条件可得4m+2(m+1)+n=5,
化简得:6m+n=3,
依题意联立方程组:,
解得,
∴y=x2+2x-3;
(2)由条件可知抛物线对称轴为直线,
∵x1=4-x2,
∴x1+x2=4,
∴.
∵y1=y2,
说明(x1,y1),(x2,y2)关于对称轴对称,
∴,
∴-m-1=4m,
解得:;
(3)∵点(-1,t)在此二次函数y=mx2+(m+1)x+n图象上,
∴t=m+(m+1)×(-1)+n=n-1,对称轴,
∵m-n=4,
∴n=m-4,
∴t=n-1=m-4-1=m-5,
∵当x≥-1时,y随x的增大而增大,
∴m>0且,
∴,
∴m+1≥2m,
解得:0<m≤1,
∴m-5≤1-5=-4,
∵t=m-5,
∴-5<t≤-4.
24.【答案】
(1)解:∵四边形BDEF内接于圆,
∴∠EDF+∠EFB=180°,
∴∠EDB=∠CFB,
∵BD是直径,
∴∠BED=90°,
∵∠C=90°,
∴△BCF∽△BED;
(2)解:BE平分∠DBF,
∴∠DBE=∠FBE,
∴EF=DE=2.5,
∵△BCF∽△BED,
∴,
设BC=4x,则BE=5x,CE=CF+EF=2+2.5=4.5,
根据勾股定理BC2+CE2=BE2,得(4x)2+4.52=(5x)2,
解得:x=1.5(舍负),
∴BC=4x=4×1.5=6;
(3)解:如图,连结OE,
∵BE平分∠DBF,OB=OE,
∴∠FBE=∠OEB,
∴OE∥BF,
又∵BD=2AD,
∴,
设DE=EF=x,圆O的半径为r,则AE=2x,
∵四边形BDEF内接于圆O,
∴∠AED=∠ABF,
∵∠A=∠A,
∴△ADE∽△AFB,
∴,
即,
解得:,
∵△BCF∽△BED,
∴,
∴.
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.以下四个城市中某天上午9时气温最低的城市是( )
杭州 温州 宁波 嘉兴
-2℃ 0℃ 1℃ -1℃
A. 杭州 B. 温州 C. 宁波 D. 嘉兴
2.6个相同正方体搭成的几何体俯视图为( )
A.
B.
C.
D.
3.截止2025年4月9日,《哪吒之魔童闹海》全球票房(含预售及海外)已破15600000000元.其中数“15600000000”用科学记数法表示为( )
A. 15.6×109 B. 1.56×1010 C. 0.156×1011 D. 1.56×1011
4.下列计算正确的是( )
A. a2+a2=a4 B. a3 a2=a6 C. a6÷a2=a3 D. (a3)3=a9
5.一次空气污染指数抽查中,收集到某地一周的数据如下:67,68,63,90,89,75,89.该组数据的中位数是( )
A. 68 B. 75 C. 89 D. 90
6.如图,在平面直角坐标系xOy中,△ABC和△A'B'C'位似,位似中心为原点O.已知点A(-1,1.5),点A′(2,-3),若△ABC的面积为2,则△A'B'C'的面积是( )
A. 2 B. 4 C. 8 D. 16
7.不等式组的解集在数轴上可表示为( )
A. B.
C. D.
8.已知一个菱形的周长是20,面积是24,则该菱形的两条对角线的长度之和为( )
A. 7 B. C. 14 D.
9.如图,一次函数y1=-2x+8的图象与反比例函数的图象相交于第一象限内的两点A(m,3n),B(m+2,n),且直线y1=-2x+8与x轴交于点C,则下列结论中正确的是( )
A. m=2
B. k=8
C. 2AB=3BC
D. 当y1>y2>0时,1<x<3
10.如图,在四边形ABCD中,∠ABC=∠ADC=90°,对角线AC和BD交于点E,若AE=4,CE=2,则BD长的最小值为( )
A. 6
B.
C. 4
D.
二、填空题:本题共6小题,每小题3分,共18分。
11.分解因式:x2-4x= .
12.一个不透明的袋子中,有5个除颜色外完全相同的小球,其中3个红球,2个白球.随机摸出一个小球,摸出红球的概率是______.
13.已知分式,若当x=1时分式的值为0,则实数a的值为______.
14.如图,AB是半圆O的直径,点C在半圆上,CD是半圆的切线,cosD=,∠CAB=30°,若CD=6,则AC的长是______.
15.“化积为方”是一个古老的几何学问题,即给定一个长方形,作一个和它面积相等的正方形,这也是证明勾股定理的一种思想方法.如图所示,在矩形ABCD中(AB>AD),以AD为边作正方形ADEF,在FE的延长线上取一点G,使得∠DGC=Rt∠,过点D作DH⊥DG交AB于点H,过点H作HK⊥GC于点K.若AF=2,BF=3FH,则FH的长为______.
16.已知二次函数y=ax2+2ax+c(a<0)的图象上有两点A(x1,y1),B(1,y2),当m-1≤x1≤m时,始终有y1<y2,则m的取值范围是______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
(1)计算:;
(2)解方程:x2+2x=8.
18.(本小题8分)
佳佳计算分式方程的过程如下:
解方程:
去分母,得1-x=-1-2………………………第①步
移项,得-x=-1-2+1…………………………第②步
合并同类项,得-x=-2…………………………第③步
系数化1,得x=2…………………………第④步
经检验,x=2是该分式方程的解.
(1)佳佳在计算过程中,第一次出现错误的步骤是______(填序号);
(2)请你写出正确的解答过程.
19.(本小题8分)
如图,平行四边形ABCD中,AE平分∠BAD交BC于点E.
(1)尺规作图:作CF平分∠BCD交AD于点F(不写作法,保留作图痕迹);
(2)求证:四边形AECF是平行四边形.
20.(本小题8分)
观察下面的等式:
第1个等式:,
第2个等式:,
第3个等式:,
第4个等式:,
……
按照以上规律,解决下列问题:
(1)写出第5个等式:______;
(2)请你猜想第n个等式(用含n的式子表示),并证明.
21.(本小题8分)
某校组织九年级学生参加研学活动,为了确定本次研学的目的地,学校对学生去向意愿进行了摸底调查(A:农家乐;B:科技馆;C:大学城).下面两幅统计图反映了抽取的部分学生对研学活动去向意愿的情况,请你根据图中的信息回答下列问题:
(1)本次调查抽取的学生总人数为______人,并补全条形统计图;
(2)求扇形统计图中选项B所对应的圆心角度数;
(3)若该校九年级的总人数为250人,试估计选择去大学城研学的总人数.
22.(本小题10分)
综合与实践:
背景:当前排球渐渐走入初中生的学习和生活中,排球运动不仅能提升身体素质,还能促进心理健康,对青少年的身心发展有着诸多益处.
排球的购买与售卖
素材1:为了能让学生日常锻炼“排球垫球”体育运动,某中学打算购进一批排球,计划购买甲品牌的排球35个,乙品牌的排球50个,共花费3550元.已知购买一个甲品牌的排球比购买一个乙品牌的排球少花20元.
素材2:某商店售卖丙品牌排球,进价为每个20元,当前售价为每个36元,每周可售出50个.经市场调查发现,售价每降低3元,每周可多售出15个.
任务1:求购买一个甲品牌、一个乙品牌的排球各需多少元?
任务2:求当一个丙品牌的排球售价为多少元时有最大利润?最大利润是多少?
23.(本小题10分)
在平面直角坐标系中,二次函数的表达式为y=mx2+(m+1)x+n,其中m-n=4.
(1)若此函数图象过点(2,5),求这个二次函数的表达式;
(2)若(x1,y1),(x2,y2)为此二次函数图象上不同的两个点,当x1=4-x2时,y1=y2,求m的值;
(3)若点(-1,t)在此二次函数图象上,当x≥-1时,y随x的增大而增大,求t的取值范围.
24.(本小题12分)
如图,点D是Rt△ABC斜边AB上的一点,以BD为直径的圆⊙O交边AC于E,F两点,连结DE,BE,BF,并且BE平分∠DBF.
(1)求证:△BCF∽△BED;
(2)若DE=2.5,CF=2,求BC的长;
(3)若BD=2AD,BF=8,求CF的长.
1.【答案】
解:由题意得:-2℃<-1℃<0℃<1℃,
∴四个城市中某天上午9时气温最低的城市是杭州.
故选:A.
2.【答案】
解:俯视图为.
故选:A.
3.【答案】
解:15600000000=1.56×1010.
故选:B.
4.【答案】
解:a2+a2=2a2,则A不符合题意;
a3 a2=a5,则B不符合题意;
a6÷a2=a4,则C不符合题意;
(a3)3=a9,则D符合题意;
故选:D.
5.【答案】
解:将这组数据重新排序为:63,67,68,75,89,89,90,则其中位数为75,
故选:B.
6.【答案】
解:∵△ABC和△A'B'C'位似,位似中心为原点O,点A(-1,1.5),点A′(2,-3),
∴△ABC与△A'B'C'的相似比为1:2,
∴△ABC与△A'B'C'的面积比为1:4,
∵△ABC的面积为2,
∴△A'B'C'的面积是8.
故选:C.
7.【答案】
解:,
解不等式①得,x<2,
解不等式②得,x≤3,
∴不等式组的解集为x<2.
∴不等式组的解集在数轴上表示,如图所示:
故选:C.
8.【答案】
解:如图所示:
∵四边形ABCD是菱形,
∴AO=CO=AC,DO=BO=BD,AC⊥BD,
∵菱形面积=BD AC=2OB OA=24,
∴OB OA=12①,
∵菱形的周长是20,
∴AB=5,
∵∠AOB=90°,
∴OB2+OA2=AB2=25②,
由①②两式可得49-2OD OA=25,
解得:OB+AO=7,
∴AC+BD=14,
故选:C.
9.【答案】
解:由条件可知,
解得,
故A选项不符合题意;
把n=2,m=1代入A(m,3n),B(m+2,n),得A(1,6),B(3,2),
则把A(1,6)代入,得,
∴k=6,
故B选项不符合题意;
∵直线y1=-2x+8与x轴交于点C,
∴令y1=0,则0=-2x+8,
解得x=4,
∴C(4,0),
∵A(1,6),B(3,2),
则,
,
则AB=2BC,
∴2AB=4BC,
故C选项不符合题意;
依题意,一次函数y1=-2x+8的图象与反比例函数的图象相交于第一象限内的两点A(1,6),B(3,2),
∴当y1>y2>0时,1<x<3,
故D选项符合题意;
故选:D.
10.【答案】
解:如图,∵∠ABC=∠ADC=90°,
∴A,B,C,D四点共圆,
∵AC为直径.
∴取AC的中点即圆心O,当弦BD⊥AC时,BD取到最小值.
∵AE=4,CE=2,
∴AC=6,
∴OB=OC=3,
∴OE=OC-CE=3-2=1,
在Rt△OEB 中,由勾股定理得,
,
∴,
即BD长的最小值为4,
故选:B.
11.【答案】
解:x2-4x=x(x-4).
故答案为:x(x-4).
12.【答案】
解:∵一个口袋里有5个除颜色外完全相同的小球,其中3个红球,2个白球,
∴摸到红球的概率是.
故答案为:.
13.【答案】
解:当x+a=0时分式值为0,
因为当x=1时分式的值为0,
所以1+a=0,
所以a=-1.
故答案为:-1.
14.【答案】
解:连接OC、BC,如图,
∵CD是半圆的切线,
∴OC⊥CD,
∴∠OCD=90°,
在Rt△OCD中,∵cosD==,
∴OD=CD=×6=10,
∴OC==8,
∵∠BOC=2∠BAC=60°,OC=OB,
∴△OCB为等边三角形,
∴BC=OC=8,
∵AB是半圆O的直径,
∴∠ACB=90°,
∵∠BAC=30°,
∴AC=BC=8.
故答案为:8.
15.【答案】
解:∵DH⊥DG,HK⊥GC,
∴∠HDG=∠DGC=∠K=90°,
∴四边形DGKH是矩形,
∵四边形ABCD是矩形,四边形ADEF是正方形,
∴∠DAB=∠DAF=90°,∠ADC=∠ADE=90°,
∴点F在AB边上,点E在CD边上,
∵CD∥AB,
∴∠DEG=∠AFE=90°,
∴∠DEG=∠DAH,
在△DEG和△DAH中,
,
∴△DEG≌△DAH(ASA),
∴DG=DH,
∴四边形DGKH是正方形,
∴DH2=DH DG=2S△CDH,
∵AB=CD,
∴AB AD=CD AD=2S△CDH,
∴DH2=AB AD,
∴AD2+AH2=DH2=AB AD,
∵BF=3FH,
∴设FH=x,则BF=3x,
∵AF=AD=DE,
∴AH=AF-FH=2-x,AB=AF+BF=3x+2,
∴22+(2-x)2=DH2=2(3x+2),
∴4+4-4x+x2=6x+4,
∴x2-10x+4=0,
∴Δ=(-10)2-4×1×4=84,
∴,
则,或(不合题意,舍去),
解得,
故答案为:.
16.【答案】
解:二次函数的对称轴为直线,
∴当x1=-1×2-1=-3或x1=1时,y1=y2,
∵a<0,
∴抛物线的开口向下,
∴离对称轴越远函数值越小.
分类讨论:①x1<-3恒成立,则y1<y2,
∴m<-3;
②x1>1恒成立,则y1<y2.
∴m-1>1.即m>2.
综上所述.m的取值范围是m<-3或m>2.
故答案为:m<-3或m>2.
17.【答案】
(1)原式=;
(2)x2+2x=8,
x2+2x-8=0,
(x+4)(x-2)=0,
x+4=0或x-2=0,
解得:x1=-4,x2=2.
18.【答案】
(1),
去分母,得1-x=-1-2(x-3),
∴第一次出现错误的是①.
故答案为:①;
(2),
去分母,得1-x=-1-2(x-3),
去括号,得1-x=-1-2x+6,
移项,得-x+2x=-1+6-1,
合并同类项,得x=4,
经检验,x=4是该分式方程的解.
19.【答案】
(1)解:图形如图所示:
(2)证明:∵四边形ABC都是平行四边形,
∴∠BAC=∠DCB,AD∥BC,
∵AE,CF方便平分∠BAD,∠BCD,
∴∠DAE=∠ECF,
∵AD∥CB,
∴∠DAE=∠AEB=∠ECF,
∴AE∥CF,
∴四边形AECF是平行四边形.
20.【答案】
(1)第5个等式为:=(),
故答案为:=();
(2)第n个式子为=(-),
右边=(-)===左边,
∴=(-),
故答案为:=(-).
21.【答案】
(1)15÷30%=50(人),
∴本次调查抽取的学生总人数为50人,
故答案为:50;
去B科技馆的人数:50-15-25=10(人),
补全条形统计图:
(2)360°×=72°,
答:选项B所对应的圆心角度数为72°;
(3)250×=125(人),
答:估计选择去大学城研学的总人数125人.
22.【答案】
解:任务1:设购买一个甲品牌排球需x元,
依题意得:35x+50(x+20)=3550,
解得:x=30,
∴30+20=50(元),
答:购买一个甲品牌的排球需30元,购买一个乙品牌的排球需50元;
任务2:设当一个丙品牌的排球降价y元时,其利润为w元,
依题意,得:w=(36-20-y)(50+)
=(16-y)(50+5y)
=-5y2+30y+800$
=-5(y-3)2+845,
当y=3,即售价为36-3=33元时利润w有最大值,最大值为845.
答:当一个丙品牌的排球售价为33元时有最大利润,最大利润是845元.
23.【答案】
(1)由条件可得4m+2(m+1)+n=5,
化简得:6m+n=3,
依题意联立方程组:,
解得,
∴y=x2+2x-3;
(2)由条件可知抛物线对称轴为直线,
∵x1=4-x2,
∴x1+x2=4,
∴.
∵y1=y2,
说明(x1,y1),(x2,y2)关于对称轴对称,
∴,
∴-m-1=4m,
解得:;
(3)∵点(-1,t)在此二次函数y=mx2+(m+1)x+n图象上,
∴t=m+(m+1)×(-1)+n=n-1,对称轴,
∵m-n=4,
∴n=m-4,
∴t=n-1=m-4-1=m-5,
∵当x≥-1时,y随x的增大而增大,
∴m>0且,
∴,
∴m+1≥2m,
解得:0<m≤1,
∴m-5≤1-5=-4,
∵t=m-5,
∴-5<t≤-4.
24.【答案】
(1)解:∵四边形BDEF内接于圆,
∴∠EDF+∠EFB=180°,
∴∠EDB=∠CFB,
∵BD是直径,
∴∠BED=90°,
∵∠C=90°,
∴△BCF∽△BED;
(2)解:BE平分∠DBF,
∴∠DBE=∠FBE,
∴EF=DE=2.5,
∵△BCF∽△BED,
∴,
设BC=4x,则BE=5x,CE=CF+EF=2+2.5=4.5,
根据勾股定理BC2+CE2=BE2,得(4x)2+4.52=(5x)2,
解得:x=1.5(舍负),
∴BC=4x=4×1.5=6;
(3)解:如图,连结OE,
∵BE平分∠DBF,OB=OE,
∴∠FBE=∠OEB,
∴OE∥BF,
又∵BD=2AD,
∴,
设DE=EF=x,圆O的半径为r,则AE=2x,
∵四边形BDEF内接于圆O,
∴∠AED=∠ABF,
∵∠A=∠A,
∴△ADE∽△AFB,
∴,
即,
解得:,
∵△BCF∽△BED,
∴,
∴.
同课章节目录
