专题强化练7 离心率及其取值范围练习-《精讲精练》26版高中同步新教材数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 专题强化练7 离心率及其取值范围练习-《精讲精练》26版高中同步新教材数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | docx | ||
| 文件大小 | 107.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-12-04 00:00:00 | ||
图片预览




文档简介
专题强化练7 离心率及其取值范围
1.已知F1,F2分别为椭圆E:+=1(a>b>0)的两个焦点,P是椭圆E上的点,PF1⊥PF2,且sin∠PF2F1=3sin∠PF1F2,则椭圆E的离心率为( )
A. B. C. D.
2.设椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,点M,N在C上(M位于第一象限),且点M,N关于原点O对称,若|MN|=|F1F2|,2|MF2|=|NF2|,则椭圆C的离心率为( )
A. B. C. D.
3.已知椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,若椭圆C上恰好有6个不同的点P,使得△PF1F2为等腰三角形,则椭圆C的离心率e的取值范围是( )
A. B.
C. D.∪
4.已知双曲线-=1(a>0,b>0),A1,A2是实轴端点,F是右焦点,B(0,b)是虚轴端点,若在线段BF上(不含端点)存在不同的两点Pi=(1,2),使得△PiA1A2(i=1,2)构成以A1A2为斜边的直角三角形,则双曲线的离心率e的取值范围是( )
A. B.
C. D.
5.已知F1,F2分别是双曲线-=1(a>0,b>0)的左、右焦点,过F1作双曲线C的渐近线y=x的垂线,垂足为P,且与双曲线C的左支交于点Q,若OQ∥PF2(O为坐标原点),则双曲线的离心率为( )
A.+1 B. C.2 D.
6.已知椭圆+=1(a>b>0)的右焦点为F(c,0),上顶点为A(0,b),直线x=上存在一点P满足(+)·=0,则椭圆的离心率的取值范围为( )
A. B.
C. D.
7.已知椭圆+=1(a>b>0)的左、右焦点分别为F1,F2,过F2的直线与椭圆交于A,B两点,P为AB的中点,4|F1P|=|AB|,tan∠APF1=,则该椭圆的离心率为( )
A. B.
C. D.
8.已知椭圆E:+=1(a>b>0),过左焦点F且不与x轴垂直的直线l交E于P,Q两点,若直线x=-上存在点T,使得△PQT是等边三角形,则E的离心率的取值范围是( )
A. B.
C. D.
9.已知F1,F2为椭圆E和双曲线C的公共焦点,P是它们的一个公共点,e1,e2分别为它们的离心率.若∠F1PF2=60°,则+的最大值为( )
A. B.
C. D.
10.已知椭圆+=1(b>a>0)内有一点(1,1),以这一点为中点的弦所在的直线方程为y=-2x+3,则椭圆的离心率为 .
11.已知P为双曲线-=1(a>0,b>0)的右支上一点,F1,F2分别为双曲线的左、右焦点,若M为△PF1F2的内心,且=+,则双曲线的离心率为 .
12.已知椭圆C:+=1(a>b>0),A是椭圆C的右顶点,O为坐标原点,若在椭圆C位于第一象限的部分上存在一点P,使AP⊥OP,则椭圆的离心率的取值范围是 .
13.已知双曲线E:-=1(a>0,b>0),A,B,F分别为双曲线的左、右顶点及右焦点,P为双曲线的右支上异于B的动点,过F作直线AP的垂线交BP于点Q,设点Q的横坐标为t,则当最大时,双曲线E的离心率为 .
14.瑞士著名数学家欧拉在1765年证明了定理:三角形的外心、重心、垂心依次位于同一条直线,且重心到外心的距离是重心到垂心距离的一半,后人称这条直线为“欧拉线”.已知直线l与y轴、双曲线-=1(a>0,b>0)的两条渐近线的三个不同交点构成集合M,且M恰为某三角形的外心、重心、垂心所构成的集合,若l的斜率为-1,则该双曲线的离心率可以是①,②,③,④,⑤中的 (填序号).
15.已知椭圆C:+=1(a>b>0)的左、右焦点分别是F1,F2,斜率为的直线l经过左焦点F1且交C于A,B两点(点A在第一象限内),设△AF1F2的内切圆半径为r1,△BF1F2的内切圆半径为r2,若=3,求椭圆的离心率.
答案与分层梯度式解析
专题强化练7 离心率及其取值范围
1.B 2.C 3.D 4.B 5.B 6.C 7.B 8.D
9.D
1.B 由题意及正弦定理得|PF1|=3|PF2|,令|PF1|=3|PF2|=3n,则3n+n=2a,又PF1⊥PF2,所以9n2+n2=4c2,可得a2=4c2,所以椭圆的离心率e===.故选B.
2.C 依题意作图如下,
由于|MN|=|F1F2|,并且线段MN,F1F2互相平分,
∴四边形MF1NF2是矩形,其中∠F1MF2=,
设|MF2|=x,则|MF1|=2a-x,
在Rt△F1MF2中,根据勾股定理,得|MF1|2+=|F1F2|2,即(2a-x)2+x2=4c2,整理得x2-2ax+2b2=0,
∵点M位于第一象限,∴|MF1|>|MF2|,即x由2|MF2|=|NF2|,得|MN|=3|MF2|,即3(a-)=2c,整理得7c2+6ac-9a2=0,即7e2+6e-9=0,解得e=,∵0名师点睛 解决圆锥曲线的离心率问题的两种办法:①若易求得a,c,则直接利用e=求解;②利用题中的几何关系得到关于a,c的齐次方程或齐次不等式,进而转化为关于e的方程或不等式并求解.
3.D 设椭圆C的上、下顶点分别为P1,P2,则△P1F1F2与△P2F1F2均为等腰三角形.
由题知,椭圆C上恰有6个不同的点P,使得△PF1F2为等腰三角形,所以在四个象限内各有一点P,使得△PF1F2为等腰三角形,根据椭圆的对称性,只考虑第一象限的情况即可.
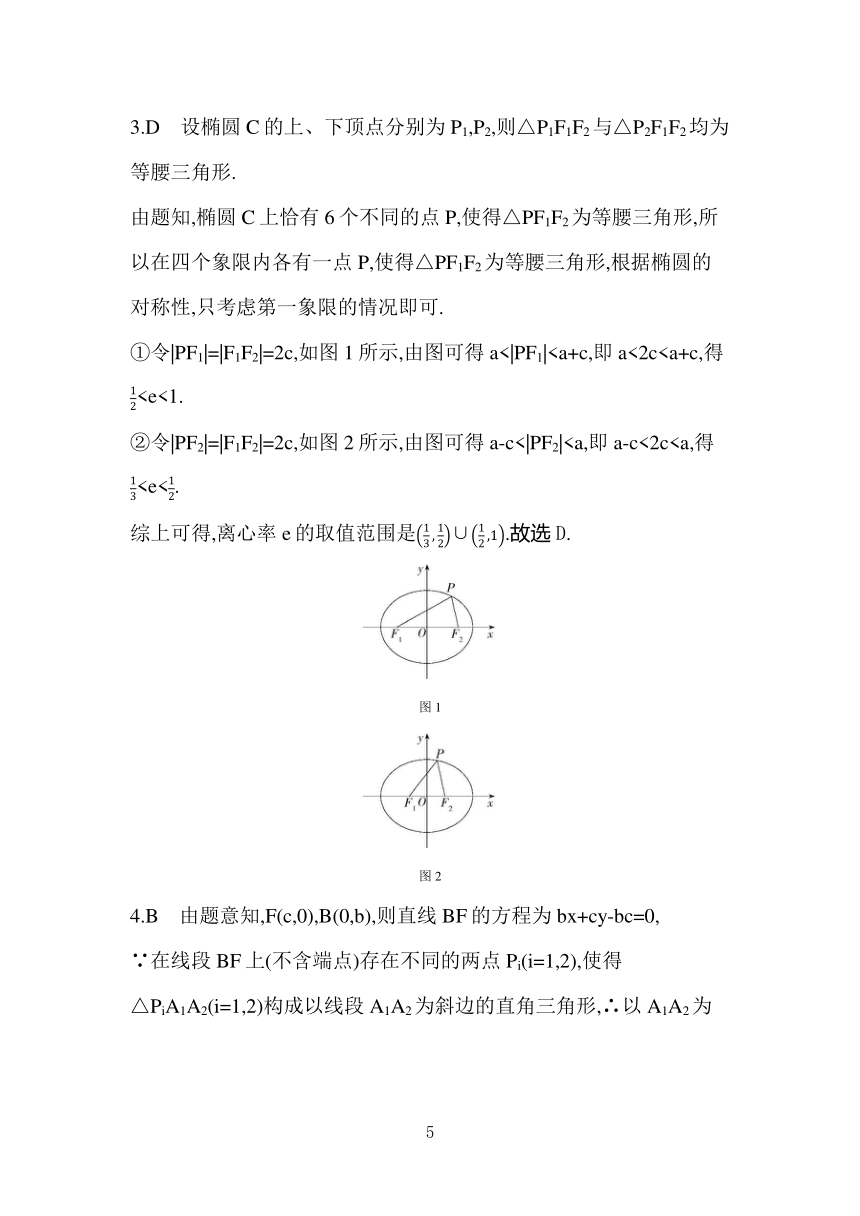
①令|PF1|=|F1F2|=2c,如图1所示,由图可得a<|PF1|②令|PF2|=|F1F2|=2c,如图2所示,由图可得a-c<|PF2|综上可得,离心率e的取值范围是∪.故选D.
图1
图2
4.B 由题意知,F(c,0),B(0,b),则直线BF的方程为bx+cy-bc=0,
∵在线段BF上(不含端点)存在不同的两点Pi(i=1,2),使得△PiA1A2(i=1,2)构成以线段A1A2为斜边的直角三角形,∴以A1A2为直径的圆与线段BF有两个交点,∴原点O到直线BF的距离小于=a,即1,∴1容易判断只有a,∴5.B 因为OQ∥PF2,O是F1F2的中点,所以Q为F1P的中点,
因为PF1⊥OP,所以点F1(-c,0)到渐近线y=x的距离d=|PF1|==b,
又|F1O|=c,所以cos∠PF1O==,
连接QF2,易知|QF1|=|PF1|=,则由双曲线的定义可知|QF2|=|QF1|+2a=+2a,
在△QF1F2中,由余弦定理的推论,得cos∠QF1F2==,整理,得a=b,所以双曲线的离心率e===,故选B.
6.C 设P,则+=+(-c,b)=,=,
由(+)·=0,可得·+(y+b)(y-b)=0,可得-2a2-b2=-y2≤0,
即a4-2a2c2-(a2-c2)c2≤0,即e4-3e2+1≤0,
解得≤e2≤,即≤e≤,由于椭圆的离心率小于1,所以≤e<1,故选C.
7.B 不妨设|AB|=2x,x>0,此时|AP|=|BP|=x,因为4|F1P|=|AB|,所以|F1P|=x,
因为tan∠APF1=>0,所以∠APF1为锐角,可得cos∠APF1=,在△AF1P中,由余弦定理得
|AF1|===x,
所以|AF1|2+|AP|2=|PF1|2,则△AF1P为直角三角形,且∠F1AP=90°,
此时|BF1|===x,而△AF1B的周长l=4a=x+x+2x,解得x=a,所以|AF1|=x=a,|AF2|=2a-|AF1|=a,
则|F1F2|=a=2c,可得e=.故选B.
8.D 由已知得点F(-c,0),设直线PQ的方程为x=my-c,其中m≠0,点P(x1,y1),Q(x2,y2),
联立可得(a2+b2m2)y2-2b2cmy-b4=0,
则Δ=4b4c2m2+4b4(a2+b2m2)=4a2b4(m2+1)>0,
由根与系数的关系可得y1+y2=,y1y2=-,
所以|PQ|=·=,
设线段PQ的中点为M(x0,y0),
则y0==,x0=my0-c=-c=-,
因为△PQT为等边三角形,所以TM⊥PQ,且直线TM的斜率为-m,
所以|TM|=·=,
且tan==,故|TM|=|PM|,
即=,整理可得=∈(0,),所以<<1.故选D.
9.D 不妨设椭圆E的方程是+=1(a1>b1>0),双曲线C的方程是-=1(a2>0,b2>0),F1,F2分别为椭圆E的左、右焦点,P在第一象限内,
由椭圆及双曲线的定义可得|PF1|+|PF2|=2a1,
|PF1|-|PF2|=2a2,∴|PF1|=a1+a2,|PF2|=a1-a2,
在△F1PF2中,由余弦定理可得,(2c)2=(a1+a2)2+(a1-a2)2-2(a1+a2)(a1-a2)cos 60°,
即4c2=+3,∴4=+,
由柯西不等式得≥,故≤×4=,即+≤,当且仅当=,即e1=,e2=时取等号.故选D.
知识延伸 柯西不等式
若a,b,c,d都是实数,则(a2+b2)(c2+d2)≥(ac+bd)2,当且仅当ad=bc时等号成立.
10.答案
解析 设以(1,1)为中点的弦所在的直线与椭圆的两个交点分别为A(x1,y1),B(x2,y2),
则=1,=1,由题意可得=-2,
将A,B的坐标代入椭圆方程,得作差可得=-,整理可得=-·=-,即-2=-,则b2=2a2,所以椭圆的离心率e===.
11.答案 2
解析 设内切圆的半径为r,如图,
由=+及三角形内切圆的性质可得,|PF1|×r=|PF2|×r+×|F1F2|×r,
∴|PF1|=|PF2|+|F1F2|,
∴|PF1|-|PF2|=|F1F2|,
又P是双曲线的右支上一点,∴2a=|F1F2|=c,∴e==2.
12.答案
解析 ∵AP⊥OP,∴点P在以AO为直径的圆上,
∵O(0,0),A(a,0),∴以AO为直径的圆的方程为+y2=,即x2+y2-ax=0,由消去y,得(b2-a2)x2+a3x-a2b2=0.
设P(m,n),0∴m+a=,ma=,∴m=.∵0,
又∵e∈(0,1),∴椭圆的离心率e的取值范围为.
13.答案 2
解析 由题意可得A(-a,0),B(a,0),易知直线AP的斜率存在,设为k,且k≠0,则直线AP的方程为y=k(x+a),与双曲线方程联立,消去y,可得(b2-a2k2)x2-2k2a3x-a4k2-a2b2=0,则-a·xP=,
解得xP=,所以yP=k(xP+a)=,
设过F(,0)且与直线AP垂直的直线为l1,则其方程为y=-(x-),
由题意可得Q为直线l1与直线BP的交点,
直线BP的方程为y=(x-a)=(x-a),
与直线l1的方程联立,可解得t=,
则==,
令q=(q>1),则==-++1=-+,
易知当q=2,即=时,取得最大值,为,
此时双曲线E的离心率e===2.
14.答案 ①③⑤
解析 易知双曲线的渐近线方程为y=±x,由题可设直线l的方程为y=-x+t(t>0),直线l与y轴的交点为A,与渐近线y=x,y=-x的交点分别为B,C.
对于y=-x+t,令x=0,可得y=t,则A(0,t),
联立可得B,联立可得C.
由题可知,若A,B,C依次为三角形的外心、重心、垂心,
则=,则=,整理得a=2b,则e===;
若A,C,B依次为三角形的外心、重心、垂心,则=,则=,整理得a=-2b,不成立;
若B,A,C依次为三角形的外心、重心、垂心,则=,则-=,整理得b=3a,则e===;
若B,C,A依次为三角形的外心、重心、垂心,则=,则-=-·,整理得a=-5b,不成立;
若C,A,B依次为三角形的外心、重心、垂心,则=,则-=,整理得b=-3a,不成立;
若C,B,A依次为三角形的外心、重心、垂心,则=,则-=-·,整理得a=5b,则e===.
故答案为①③⑤.
15.解析 如图所示,由椭圆的定义可得|AF1|+|AF2|=2a,|BF1|+|BF2|=2a.
设△AF1F2的面积为S1,△BF1F2的面积为S2,因为=3,
所以==,
即=-=3,即yA=-3yB.
易得直线l:x=2y-c,联立椭圆与直线l的方程,可得消去x,可得(a2+4b2)y2-4b2cy-b4=0,
所以yA+yB=,yA·yB=.
令-=λ,则2-====,
又λ=3,故2-=-=,即e2=,故e=,即椭圆的离心率为.
7
1.已知F1,F2分别为椭圆E:+=1(a>b>0)的两个焦点,P是椭圆E上的点,PF1⊥PF2,且sin∠PF2F1=3sin∠PF1F2,则椭圆E的离心率为( )
A. B. C. D.
2.设椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,点M,N在C上(M位于第一象限),且点M,N关于原点O对称,若|MN|=|F1F2|,2|MF2|=|NF2|,则椭圆C的离心率为( )
A. B. C. D.
3.已知椭圆C:+=1(a>b>0)的左、右焦点分别为F1,F2,若椭圆C上恰好有6个不同的点P,使得△PF1F2为等腰三角形,则椭圆C的离心率e的取值范围是( )
A. B.
C. D.∪
4.已知双曲线-=1(a>0,b>0),A1,A2是实轴端点,F是右焦点,B(0,b)是虚轴端点,若在线段BF上(不含端点)存在不同的两点Pi=(1,2),使得△PiA1A2(i=1,2)构成以A1A2为斜边的直角三角形,则双曲线的离心率e的取值范围是( )
A. B.
C. D.
5.已知F1,F2分别是双曲线-=1(a>0,b>0)的左、右焦点,过F1作双曲线C的渐近线y=x的垂线,垂足为P,且与双曲线C的左支交于点Q,若OQ∥PF2(O为坐标原点),则双曲线的离心率为( )
A.+1 B. C.2 D.
6.已知椭圆+=1(a>b>0)的右焦点为F(c,0),上顶点为A(0,b),直线x=上存在一点P满足(+)·=0,则椭圆的离心率的取值范围为( )
A. B.
C. D.
7.已知椭圆+=1(a>b>0)的左、右焦点分别为F1,F2,过F2的直线与椭圆交于A,B两点,P为AB的中点,4|F1P|=|AB|,tan∠APF1=,则该椭圆的离心率为( )
A. B.
C. D.
8.已知椭圆E:+=1(a>b>0),过左焦点F且不与x轴垂直的直线l交E于P,Q两点,若直线x=-上存在点T,使得△PQT是等边三角形,则E的离心率的取值范围是( )
A. B.
C. D.
9.已知F1,F2为椭圆E和双曲线C的公共焦点,P是它们的一个公共点,e1,e2分别为它们的离心率.若∠F1PF2=60°,则+的最大值为( )
A. B.
C. D.
10.已知椭圆+=1(b>a>0)内有一点(1,1),以这一点为中点的弦所在的直线方程为y=-2x+3,则椭圆的离心率为 .
11.已知P为双曲线-=1(a>0,b>0)的右支上一点,F1,F2分别为双曲线的左、右焦点,若M为△PF1F2的内心,且=+,则双曲线的离心率为 .
12.已知椭圆C:+=1(a>b>0),A是椭圆C的右顶点,O为坐标原点,若在椭圆C位于第一象限的部分上存在一点P,使AP⊥OP,则椭圆的离心率的取值范围是 .
13.已知双曲线E:-=1(a>0,b>0),A,B,F分别为双曲线的左、右顶点及右焦点,P为双曲线的右支上异于B的动点,过F作直线AP的垂线交BP于点Q,设点Q的横坐标为t,则当最大时,双曲线E的离心率为 .
14.瑞士著名数学家欧拉在1765年证明了定理:三角形的外心、重心、垂心依次位于同一条直线,且重心到外心的距离是重心到垂心距离的一半,后人称这条直线为“欧拉线”.已知直线l与y轴、双曲线-=1(a>0,b>0)的两条渐近线的三个不同交点构成集合M,且M恰为某三角形的外心、重心、垂心所构成的集合,若l的斜率为-1,则该双曲线的离心率可以是①,②,③,④,⑤中的 (填序号).
15.已知椭圆C:+=1(a>b>0)的左、右焦点分别是F1,F2,斜率为的直线l经过左焦点F1且交C于A,B两点(点A在第一象限内),设△AF1F2的内切圆半径为r1,△BF1F2的内切圆半径为r2,若=3,求椭圆的离心率.
答案与分层梯度式解析
专题强化练7 离心率及其取值范围
1.B 2.C 3.D 4.B 5.B 6.C 7.B 8.D
9.D
1.B 由题意及正弦定理得|PF1|=3|PF2|,令|PF1|=3|PF2|=3n,则3n+n=2a,又PF1⊥PF2,所以9n2+n2=4c2,可得a2=4c2,所以椭圆的离心率e===.故选B.
2.C 依题意作图如下,
由于|MN|=|F1F2|,并且线段MN,F1F2互相平分,
∴四边形MF1NF2是矩形,其中∠F1MF2=,
设|MF2|=x,则|MF1|=2a-x,
在Rt△F1MF2中,根据勾股定理,得|MF1|2+=|F1F2|2,即(2a-x)2+x2=4c2,整理得x2-2ax+2b2=0,
∵点M位于第一象限,∴|MF1|>|MF2|,即x
3.D 设椭圆C的上、下顶点分别为P1,P2,则△P1F1F2与△P2F1F2均为等腰三角形.
由题知,椭圆C上恰有6个不同的点P,使得△PF1F2为等腰三角形,所以在四个象限内各有一点P,使得△PF1F2为等腰三角形,根据椭圆的对称性,只考虑第一象限的情况即可.
①令|PF1|=|F1F2|=2c,如图1所示,由图可得a<|PF1|
图1
图2
4.B 由题意知,F(c,0),B(0,b),则直线BF的方程为bx+cy-bc=0,
∵在线段BF上(不含端点)存在不同的两点Pi(i=1,2),使得△PiA1A2(i=1,2)构成以线段A1A2为斜边的直角三角形,∴以A1A2为直径的圆与线段BF有两个交点,∴原点O到直线BF的距离小于=a,即
因为PF1⊥OP,所以点F1(-c,0)到渐近线y=x的距离d=|PF1|==b,
又|F1O|=c,所以cos∠PF1O==,
连接QF2,易知|QF1|=|PF1|=,则由双曲线的定义可知|QF2|=|QF1|+2a=+2a,
在△QF1F2中,由余弦定理的推论,得cos∠QF1F2==,整理,得a=b,所以双曲线的离心率e===,故选B.
6.C 设P,则+=+(-c,b)=,=,
由(+)·=0,可得·+(y+b)(y-b)=0,可得-2a2-b2=-y2≤0,
即a4-2a2c2-(a2-c2)c2≤0,即e4-3e2+1≤0,
解得≤e2≤,即≤e≤,由于椭圆的离心率小于1,所以≤e<1,故选C.
7.B 不妨设|AB|=2x,x>0,此时|AP|=|BP|=x,因为4|F1P|=|AB|,所以|F1P|=x,
因为tan∠APF1=>0,所以∠APF1为锐角,可得cos∠APF1=,在△AF1P中,由余弦定理得
|AF1|===x,
所以|AF1|2+|AP|2=|PF1|2,则△AF1P为直角三角形,且∠F1AP=90°,
此时|BF1|===x,而△AF1B的周长l=4a=x+x+2x,解得x=a,所以|AF1|=x=a,|AF2|=2a-|AF1|=a,
则|F1F2|=a=2c,可得e=.故选B.
8.D 由已知得点F(-c,0),设直线PQ的方程为x=my-c,其中m≠0,点P(x1,y1),Q(x2,y2),
联立可得(a2+b2m2)y2-2b2cmy-b4=0,
则Δ=4b4c2m2+4b4(a2+b2m2)=4a2b4(m2+1)>0,
由根与系数的关系可得y1+y2=,y1y2=-,
所以|PQ|=·=,
设线段PQ的中点为M(x0,y0),
则y0==,x0=my0-c=-c=-,
因为△PQT为等边三角形,所以TM⊥PQ,且直线TM的斜率为-m,
所以|TM|=·=,
且tan==,故|TM|=|PM|,
即=,整理可得=∈(0,),所以<<1.故选D.
9.D 不妨设椭圆E的方程是+=1(a1>b1>0),双曲线C的方程是-=1(a2>0,b2>0),F1,F2分别为椭圆E的左、右焦点,P在第一象限内,
由椭圆及双曲线的定义可得|PF1|+|PF2|=2a1,
|PF1|-|PF2|=2a2,∴|PF1|=a1+a2,|PF2|=a1-a2,
在△F1PF2中,由余弦定理可得,(2c)2=(a1+a2)2+(a1-a2)2-2(a1+a2)(a1-a2)cos 60°,
即4c2=+3,∴4=+,
由柯西不等式得≥,故≤×4=,即+≤,当且仅当=,即e1=,e2=时取等号.故选D.
知识延伸 柯西不等式
若a,b,c,d都是实数,则(a2+b2)(c2+d2)≥(ac+bd)2,当且仅当ad=bc时等号成立.
10.答案
解析 设以(1,1)为中点的弦所在的直线与椭圆的两个交点分别为A(x1,y1),B(x2,y2),
则=1,=1,由题意可得=-2,
将A,B的坐标代入椭圆方程,得作差可得=-,整理可得=-·=-,即-2=-,则b2=2a2,所以椭圆的离心率e===.
11.答案 2
解析 设内切圆的半径为r,如图,
由=+及三角形内切圆的性质可得,|PF1|×r=|PF2|×r+×|F1F2|×r,
∴|PF1|=|PF2|+|F1F2|,
∴|PF1|-|PF2|=|F1F2|,
又P是双曲线的右支上一点,∴2a=|F1F2|=c,∴e==2.
12.答案
解析 ∵AP⊥OP,∴点P在以AO为直径的圆上,
∵O(0,0),A(a,0),∴以AO为直径的圆的方程为+y2=,即x2+y2-ax=0,由消去y,得(b2-a2)x2+a3x-a2b2=0.
设P(m,n),0
又∵e∈(0,1),∴椭圆的离心率e的取值范围为.
13.答案 2
解析 由题意可得A(-a,0),B(a,0),易知直线AP的斜率存在,设为k,且k≠0,则直线AP的方程为y=k(x+a),与双曲线方程联立,消去y,可得(b2-a2k2)x2-2k2a3x-a4k2-a2b2=0,则-a·xP=,
解得xP=,所以yP=k(xP+a)=,
设过F(,0)且与直线AP垂直的直线为l1,则其方程为y=-(x-),
由题意可得Q为直线l1与直线BP的交点,
直线BP的方程为y=(x-a)=(x-a),
与直线l1的方程联立,可解得t=,
则==,
令q=(q>1),则==-++1=-+,
易知当q=2,即=时,取得最大值,为,
此时双曲线E的离心率e===2.
14.答案 ①③⑤
解析 易知双曲线的渐近线方程为y=±x,由题可设直线l的方程为y=-x+t(t>0),直线l与y轴的交点为A,与渐近线y=x,y=-x的交点分别为B,C.
对于y=-x+t,令x=0,可得y=t,则A(0,t),
联立可得B,联立可得C.
由题可知,若A,B,C依次为三角形的外心、重心、垂心,
则=,则=,整理得a=2b,则e===;
若A,C,B依次为三角形的外心、重心、垂心,则=,则=,整理得a=-2b,不成立;
若B,A,C依次为三角形的外心、重心、垂心,则=,则-=,整理得b=3a,则e===;
若B,C,A依次为三角形的外心、重心、垂心,则=,则-=-·,整理得a=-5b,不成立;
若C,A,B依次为三角形的外心、重心、垂心,则=,则-=,整理得b=-3a,不成立;
若C,B,A依次为三角形的外心、重心、垂心,则=,则-=-·,整理得a=5b,则e===.
故答案为①③⑤.
15.解析 如图所示,由椭圆的定义可得|AF1|+|AF2|=2a,|BF1|+|BF2|=2a.
设△AF1F2的面积为S1,△BF1F2的面积为S2,因为=3,
所以==,
即=-=3,即yA=-3yB.
易得直线l:x=2y-c,联立椭圆与直线l的方程,可得消去x,可得(a2+4b2)y2-4b2cy-b4=0,
所以yA+yB=,yA·yB=.
令-=λ,则2-====,
又λ=3,故2-=-=,即e2=,故e=,即椭圆的离心率为.
7
