17.2 第2课时 利用完全平方公式分解因式 教案 2025-2026人教版数学八年级上册
文档属性
| 名称 | 17.2 第2课时 利用完全平方公式分解因式 教案 2025-2026人教版数学八年级上册 | 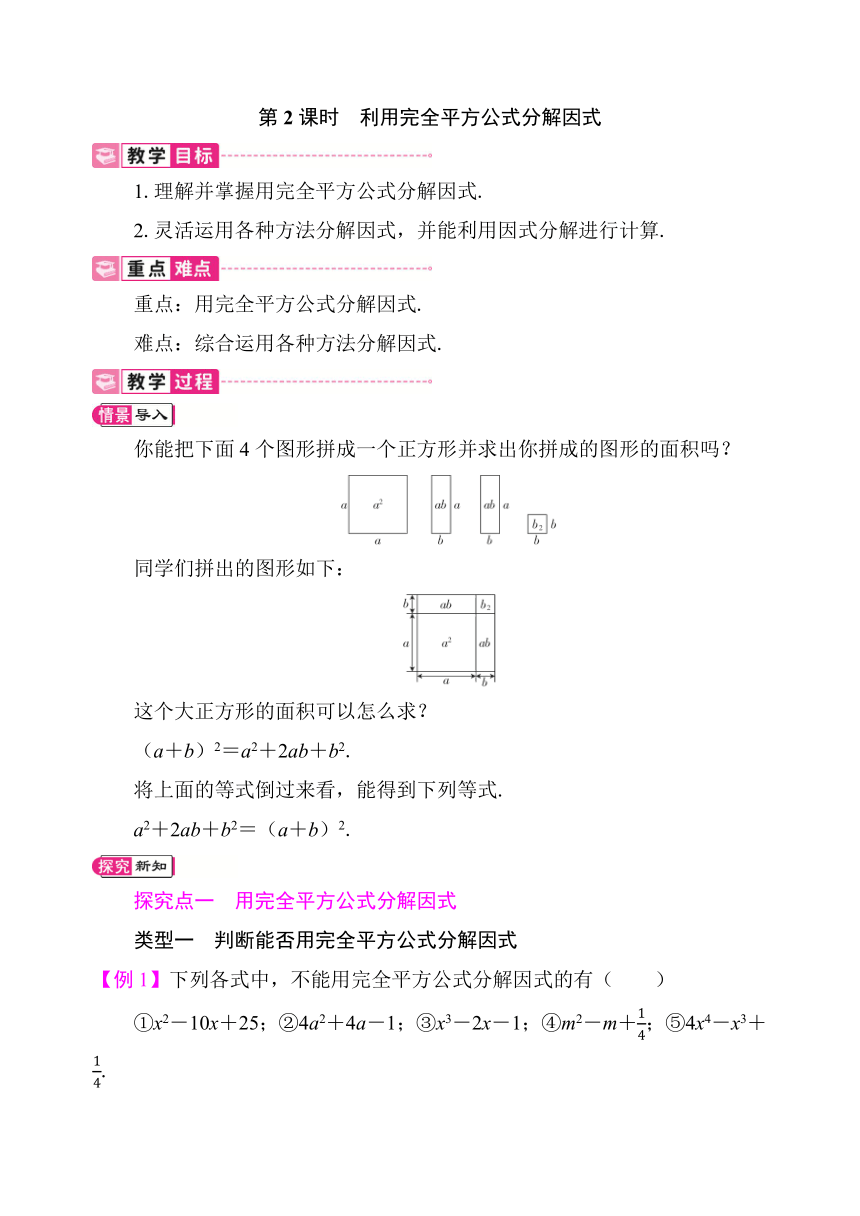 | |
| 格式 | docx | ||
| 文件大小 | 102.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 21:15:58 | ||
图片预览


文档简介
第2课时 利用完全平方公式分解因式
1.理解并掌握用完全平方公式分解因式.
2.灵活运用各种方法分解因式,并能利用因式分解进行计算.
重点:用完全平方公式分解因式.
难点:综合运用各种方法分解因式.
你能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
同学们拼出的图形如下:
这个大正方形的面积可以怎么求?
(a+b)2=a2+2ab+b2.
将上面的等式倒过来看,能得到下列等式.
a2+2ab+b2=(a+b)2.
探究点一 用完全平方公式分解因式
类型一 判断能否用完全平方公式分解因式
【例1】下列各式中,不能用完全平方公式分解因式的有( )
①x2-10x+25;②4a2+4a-1;③x3-2x-1;④m2-m+;⑤4x4-x3+.
A.1个 B.2个
C.3个 D.4个
【解析】①x2-10x+25=(x-5)2,④m2-m+=均能用完全平方公式分解因式;②4a2+4a-1,③x3-2x-1,⑤4x4-x3+均不能用完全平方公式分解因式.故符合题意的有3个.
【答案】C
【方法总结】观察式子的特点,根据“两端平方和,中间积2倍”即可判断.
类型二 用完全平方公式分解因式
【例2】用完全平方公式分解因式:
(1)x2-x+.
(2)(m+n)2-6(m+n)+9.
【解析】根据完全平方公式的特点分解因式即可.
【解】(1)原式=(x-)2.
(2)原式=(m+n-3)2.
类型三 用完全平方公式分解因式的应用
【例3】已知a,b,c分别是△ABC三边的长,且a2+2b2+c2-2b(a+c)=0.请判断△ABC的形状,并说明理由.
【解析】首先利用完全平方公式分组进行因式分解,进一步分析探讨三边关系得出结论即可.
【解】△ABC是等边三角形.理由如下:
由a2+2b2+c2-2b(a+c)=0,
得a2-2ab+b2+b2-2bc+c2=0,
即(a-b)2+(b-c)2=0,
∴a-b=0,b-c=0,
∴a=b=c,
∴△ABC是等边三角形.
【方法总结】将原式写成两个完全平方式,转化为非负数的和的形式,然后利用非负数的性质进行解答,这是解决此类问题的一般思路.
探究点二 提公因式法和公式法的综合
【例4】分解因式:
(1)3x2-6xy+3y2.
(2)-a3+4a2b-4ab2.
【解析】如果多项式有公因式,先提出公因式,再观察是否用公式法.
【解】(1)原式=3(x2-2xy+y2)
=3(x-y)2.
(2)原式=-a(a2-4ab+4b2)
=-a(a-2b)2.
【方法总结】观察多项式的特点,有公因式的先提出公因式,再观察是否能用公式法分解因式.
1.将多项式6xy2-9x2y-y3分解因式,最后的结果为 .
2.将下列各式分解因式:
(1)xy3-2x2y2+x3y.
(2)-a3+a2b-ab2.
(3)9(x+y)2-6(x+y)+1.
3.已知长方形的长为a,宽为b,周长为16,长与宽的平方和为34.
(1)求此长方形的面积.
(2)求a3b+2a2b2+ab3的值.
第2课时 利用完全平方公式分解因式
1.利用完全平方公式分解因式:a2+2ab+b2=(a+b)2,a2-2ab+b2=(a-b)2.
2.文字叙述:两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
本节课学习了用完全平方公式分解因式,要注意公式的特点.
本节课是在用平方差公式分解因式的基础上继续用完全平方公式分解因式,实际上就是把乘法公式中的完全平方公式的等号两边互换位置.学生对该过程掌握得比较好,但是当多项式中有公因式时,常常会在提出公因式后忘记继续分解因式.
答案
课堂训练
1.-y(3x-y)2
2.解:(1)原式=xy(y2-2xy+x2)
=xy(y-x)2.
(2)原式=-a
=-a.
(3)原式=[3(x+y)-1]2
=(3x+3y-1)2.
3.解:(1)∵a+b=16÷2=8,
∴(a+b)2=a2+2ab+b2=64.
∵a2+b2=34,
∴ab=15,即长方形的面积为15.
(2)a3b+2a2b2+ab3
=ab(a2+2ab+b2)
=ab(a+b)2
=15×82
=960.
1.理解并掌握用完全平方公式分解因式.
2.灵活运用各种方法分解因式,并能利用因式分解进行计算.
重点:用完全平方公式分解因式.
难点:综合运用各种方法分解因式.
你能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
同学们拼出的图形如下:
这个大正方形的面积可以怎么求?
(a+b)2=a2+2ab+b2.
将上面的等式倒过来看,能得到下列等式.
a2+2ab+b2=(a+b)2.
探究点一 用完全平方公式分解因式
类型一 判断能否用完全平方公式分解因式
【例1】下列各式中,不能用完全平方公式分解因式的有( )
①x2-10x+25;②4a2+4a-1;③x3-2x-1;④m2-m+;⑤4x4-x3+.
A.1个 B.2个
C.3个 D.4个
【解析】①x2-10x+25=(x-5)2,④m2-m+=均能用完全平方公式分解因式;②4a2+4a-1,③x3-2x-1,⑤4x4-x3+均不能用完全平方公式分解因式.故符合题意的有3个.
【答案】C
【方法总结】观察式子的特点,根据“两端平方和,中间积2倍”即可判断.
类型二 用完全平方公式分解因式
【例2】用完全平方公式分解因式:
(1)x2-x+.
(2)(m+n)2-6(m+n)+9.
【解析】根据完全平方公式的特点分解因式即可.
【解】(1)原式=(x-)2.
(2)原式=(m+n-3)2.
类型三 用完全平方公式分解因式的应用
【例3】已知a,b,c分别是△ABC三边的长,且a2+2b2+c2-2b(a+c)=0.请判断△ABC的形状,并说明理由.
【解析】首先利用完全平方公式分组进行因式分解,进一步分析探讨三边关系得出结论即可.
【解】△ABC是等边三角形.理由如下:
由a2+2b2+c2-2b(a+c)=0,
得a2-2ab+b2+b2-2bc+c2=0,
即(a-b)2+(b-c)2=0,
∴a-b=0,b-c=0,
∴a=b=c,
∴△ABC是等边三角形.
【方法总结】将原式写成两个完全平方式,转化为非负数的和的形式,然后利用非负数的性质进行解答,这是解决此类问题的一般思路.
探究点二 提公因式法和公式法的综合
【例4】分解因式:
(1)3x2-6xy+3y2.
(2)-a3+4a2b-4ab2.
【解析】如果多项式有公因式,先提出公因式,再观察是否用公式法.
【解】(1)原式=3(x2-2xy+y2)
=3(x-y)2.
(2)原式=-a(a2-4ab+4b2)
=-a(a-2b)2.
【方法总结】观察多项式的特点,有公因式的先提出公因式,再观察是否能用公式法分解因式.
1.将多项式6xy2-9x2y-y3分解因式,最后的结果为 .
2.将下列各式分解因式:
(1)xy3-2x2y2+x3y.
(2)-a3+a2b-ab2.
(3)9(x+y)2-6(x+y)+1.
3.已知长方形的长为a,宽为b,周长为16,长与宽的平方和为34.
(1)求此长方形的面积.
(2)求a3b+2a2b2+ab3的值.
第2课时 利用完全平方公式分解因式
1.利用完全平方公式分解因式:a2+2ab+b2=(a+b)2,a2-2ab+b2=(a-b)2.
2.文字叙述:两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
本节课学习了用完全平方公式分解因式,要注意公式的特点.
本节课是在用平方差公式分解因式的基础上继续用完全平方公式分解因式,实际上就是把乘法公式中的完全平方公式的等号两边互换位置.学生对该过程掌握得比较好,但是当多项式中有公因式时,常常会在提出公因式后忘记继续分解因式.
答案
课堂训练
1.-y(3x-y)2
2.解:(1)原式=xy(y2-2xy+x2)
=xy(y-x)2.
(2)原式=-a
=-a.
(3)原式=[3(x+y)-1]2
=(3x+3y-1)2.
3.解:(1)∵a+b=16÷2=8,
∴(a+b)2=a2+2ab+b2=64.
∵a2+b2=34,
∴ab=15,即长方形的面积为15.
(2)a3b+2a2b2+ab3
=ab(a2+2ab+b2)
=ab(a+b)2
=15×82
=960.
同课章节目录
