第二十四章 圆(单元测试.含解析)-2025-2026学年九年级上册数学人教版
文档属性
| 名称 | 第二十四章 圆(单元测试.含解析)-2025-2026学年九年级上册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-12 18:14:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二十四章 圆
一.选择题(共10小题)
1.(2025 绵阳)如图,在边长为2的正六边形中,连接,点在上运动,点为的中点,当△的周长最小时,
A. B. C.12 D.13
2.(2025 绵阳)将一把折扇展开,可抽象成一个扇形,若该扇形的半径为2,弧长为,则扇形的圆心角大小为
A. B. C. D.
3.(2025 当阳市模拟)已知的半径为5,点在内,则的长可能是
A.7 B.6 C.5 D.4
4.(2025 任城区一模)如图,、是的两条直径,是劣弧的中点,若,则的度数是
A. B. C. D.
5.(2025 高邮市校级模拟)已知的半径是6,点是平面内一点且,则点与的位置关系是
A.圆内 B.圆外 C.圆上 D.无法确定
6.(2025 雁塔区校级四模)如图,四边形内接于,已知点为的中点,若,则的度数为
A. B. C. D.
7.(2025 沙坪坝区校级一模)如图,是的直径,过的延长线上的点作的切线,切点为,点是上一点,连接,,若,则等于
A. B. C. D.
8.(2025 丛台区校级三模)如图,在中,满足,则下列对弦与弦大小关系表述正确的是
A. B. C. D.无法确定
9.(2025 临邑县一模)如图,在矩形中,,以为直径作,将矩形绕点旋转,使所得矩形的边与相切,切点为,边与相交于点.若,则长为
A.9 B.10 C. D.12
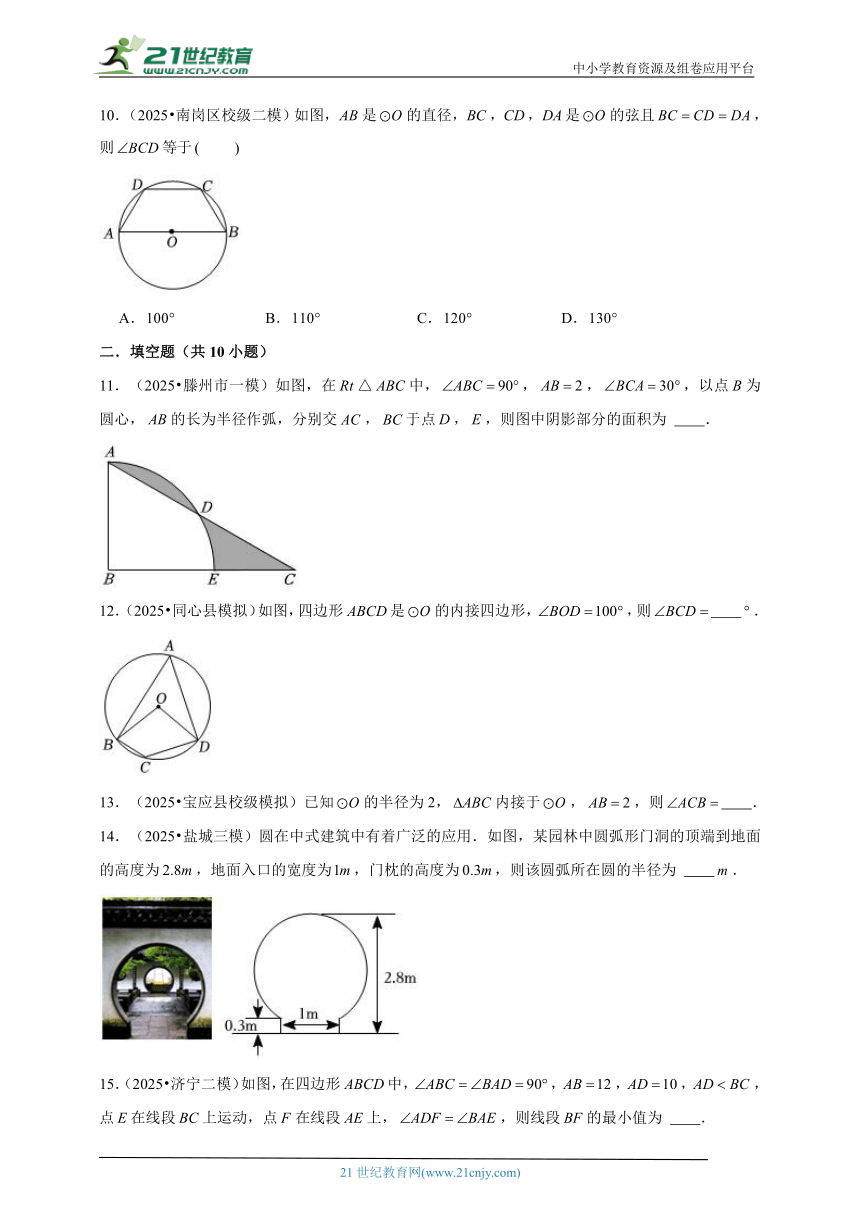
10.(2025 南岗区校级二模)如图,是的直径,,,是的弦且,则等于
A. B. C. D.
二.填空题(共10小题)
11.(2025 滕州市一模)如图,在△中,,,,以点为圆心,的长为半径作弧,分别交,于点,,则图中阴影部分的面积为 .
12.(2025 同心县模拟)如图,四边形是的内接四边形,,则 .
13.(2025 宝应县校级模拟)已知的半径为2,内接于,,则 .
14.(2025 盐城三模)圆在中式建筑中有着广泛的应用.如图,某园林中圆弧形门洞的顶端到地面的高度为,地面入口的宽度为,门枕的高度为,则该圆弧所在圆的半径为 .
15.(2025 济宁二模)如图,在四边形中,,,,,点在线段上运动,点在线段上,,则线段的最小值为 .
16.(2025 盱眙县校级模拟)《九章算术》第一章“方田”介绍了扇形面积计算方法,其中这样一道题:“今有宛田,下周三十步,径十六步,问为田几何?”意思是:有一块扇形状的田,弧长为30步,其所在圆的直径是16步,则这块田的面积为 平方步.
17.(2025 东莞市校级二模)如图,的半径为5,弦的长为8,是弦上的一个动点,则线段的长的最小值为 .
18.(2025 浙江模拟)如图,正方形的边长为2,以边上的动点为圆心,为半径作圆,将沿翻折至△,若过△一边上的中点,则的半径为 .
19.(2025 金凤区校级二模)如图,、、、为一个正多边形的顶点,为正多边形的中心,若,则这个正多边形的边数为 .
20.(2025 佳木斯三模)日常生活中常见的装饰盘由圆盘和支架组成(如图,它可以看作如图2所示的几何图形.已知,,垂足为点,,垂足为点,,的半径,则圆盘离桌面最近的距离是 .
三.解答题(共5小题)
21.(2025 绵阳)如图,为△的外接圆,弦,垂足为,直径交于点,连接,.若,.
(1)证明:四边形为平行四边形;
(2)求为值;
(3)求的值.
22.(2025 凉山州模拟)如图,在△中,,以为直径的交于点,为的中点,连接并延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求长.
23.(2025 武威三模)如图,以四边形的对角线为直径作圆,圆心为,过点作的延长线于点,已知平分.
(1)求证:是切线;
(2)若,,求的半径和的长.
24.(2025 烟台一模)如图,圆内接四边形的对角线,交于点,平分,.
(1)求证:为圆的直径;
(2)过点作交的延长线于点,若,,求此圆半径的长.
25.(2025 哈尔滨模拟)如图,内接于圆,连接.
(1)如图1,求证:;
(2)如图2,于交圆于,于,求证:;
(3)如图3,在(2)的条件下,若平分,延长交于,,,求长.
第二十四章 圆
参考答案与试题解析
一.选择题(共10小题)
1.(2025 绵阳)如图,在边长为2的正六边形中,连接,点在上运动,点为的中点,当△的周长最小时,
A. B. C.12 D.13
【答案】
【考点】轴对称最短路线问题;正多边形和圆
【专题】运算能力;多边形与平行四边形
【分析】要使△的周长最小时,最小,利用正六边形的性质可得点关于的对称点为点,连接交于点,连接,,那么有,最小,再根据正六边形的性质和勾股定理计算即可.
【解答】解:如图,
要使△的周长的最小,即最小,
利用正六边形的性质可得点关于的对称点为点,连接交于点,连接,,
那么有,最小,
,,
,
,,
,
故当△的周长最小时,.
故选:.
【点评】此题主要考查了正多边形和圆以及轴对称最短路线问题,得出点位置是解题关键.
2.(2025 绵阳)将一把折扇展开,可抽象成一个扇形,若该扇形的半径为2,弧长为,则扇形的圆心角大小为
A. B. C. D.
【答案】
【考点】弧长的计算
【专题】运算能力;与圆有关的计算
【分析】依据题意,根据弧长公式进行代入计算即可得解.
【解答】解:由题意,弧长,且,
.
故选:.
【点评】本题主要考查了弧长的计算,解题时要能熟练掌握并能准确计算是关键.
3.(2025 当阳市模拟)已知的半径为5,点在内,则的长可能是
A.7 B.6 C.5 D.4
【答案】
【考点】点与圆的位置关系
【专题】与圆有关的位置关系;推理能力
【分析】根据点在圆内,点到圆心的距离小于圆的半径进行判断.
【解答】解:的半径为5,点在内,
.
故选:.
【点评】本题考查了点与圆的位置关系:设的半径为,点到圆心的距离,则有:点在圆外;点在圆上;点在圆内.
4.(2025 任城区一模)如图,、是的两条直径,是劣弧的中点,若,则的度数是
A. B. C. D.
【答案】
【考点】圆心角、弧、弦的关系;圆周角定理
【专题】与圆有关的计算;推理能力
【分析】首先根据“同弧或等弧所对的弦长相等,对的圆心角也相等”求得,再根据等腰三角形“等边对等角”的性质求解即可.
【解答】解:如图,连接,
是劣弧的中点,
即弧弧,
,
,
,
,
,
即.
故选:.
【点评】本题主要考查了弧与圆心角的关系、等腰三角形的性质、三角形内角和定理等知识,熟练掌握相关知识并灵活运用是解题关键.
5.(2025 高邮市校级模拟)已知的半径是6,点是平面内一点且,则点与的位置关系是
A.圆内 B.圆外 C.圆上 D.无法确定
【答案】
【考点】点与圆的位置关系
【专题】与圆有关的位置关系;推理能力
【分析】根据点与圆的位置关系的判定方法对点与的位置关系进行判断即可.
【解答】解:的半径为6,,
点到圆心的距离大于圆的半径,
点在外.
故选:.
【点评】本题考查了点与圆的位置关系,熟知设的半径为,点到圆心的距离,则点在圆外;点在圆上;点在圆内是解题的关键.
6.(2025 雁塔区校级四模)如图,四边形内接于,已知点为的中点,若,则的度数为
A. B. C. D.
【答案】
【考点】圆心角、弧、弦的关系;圆周角定理;圆内接四边形的性质
【专题】推理能力;圆的有关概念及性质
【分析】根据圆内接四边形的性质得到,根据等腰三角形的性质即可得到结论.
【解答】解:四边形内接于,,
,
点为的中点,
,
,
故选:.
【点评】本题考查的是圆内接四边形的性质,圆心角、弧、弦的关系、圆周角定理的应用,掌握圆心角、弧、弦的关系定理和圆周角定理是解题的关键.
7.(2025 沙坪坝区校级一模)如图,是的直径,过的延长线上的点作的切线,切点为,点是上一点,连接,,若,则等于
A. B. C. D.
【答案】
【考点】圆周角定理;切线的性质
【专题】与圆有关的位置关系;推理能力
【分析】连接,如图,先根据切线的性质得到,再根据圆周角定理得到,然后利用互余可表示出.
【解答】解:连接,如图,
为的切线,
,
,
,
.
故选:.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理.
8.(2025 丛台区校级三模)如图,在中,满足,则下列对弦与弦大小关系表述正确的是
A. B. C. D.无法确定
【答案】
【考点】三角形三边关系;圆心角、弧、弦的关系
【专题】圆的有关概念及性质;推理能力
【分析】如图,取弧的中点,连接,.证明,再利用三角形的三边关系解决问题.
【解答】解:如图,取弧的中点,连接,.
,,
,
,
,
.
故选:.
【点评】本题考查圆心角,弧,弦之间等分关系,三角形的三边关系等知识,解题的关键是理解题意正确作出辅助线.
9.(2025 临邑县一模)如图,在矩形中,,以为直径作,将矩形绕点旋转,使所得矩形的边与相切,切点为,边与相交于点.若,则长为
A.9 B.10 C. D.12
【答案】
【考点】圆周角定理;矩形的性质;切线的判定与性质;旋转的性质
【专题】平移、旋转与对称;矩形 菱形 正方形;计算题;运算能力;推理能力
【分析】连接,延长交于点,设,则,由勾股定理得出,解得,则得出答案.
【解答】解:连接,延长交于点,
与相切,
,
又矩形中,,
,
,
矩形绕点旋转所得矩形为,
,,,
四边形为矩形,
,
设,则,
,
,
解得,
.
故选:.
【点评】本题主要考查圆的切线的判定与性质,解题的关键是掌握矩形的判定与性质、旋转的性质、切线的性质、垂径定理等知识点.
10.(2025 南岗区校级二模)如图,是的直径,,,是的弦且,则等于
A. B. C. D.
【答案】
【考点】圆心角、弧、弦的关系;圆周角定理
【专题】圆的有关概念及性质;推理能力
【分析】由已知可得,弦、、三等分半圆,从而不难求得的度数.
【解答】解:连接、,
,
,
弦、、三等分半圆,
弦和和对的圆心角均为,
.
故选:.
【点评】本题利用了弧、弦与圆心角的关系求解,注意半圆对的圆心角为.
二.填空题(共10小题)
11.(2025 滕州市一模)如图,在△中,,,,以点为圆心,的长为半径作弧,分别交,于点,,则图中阴影部分的面积为 .
【考点】含30度角的直角三角形;扇形面积的计算
【专题】与圆有关的计算;应用意识
【分析】连接,过点作,垂足为,找出即可求出答案.
【解答】解:连接,过点作,垂足为,如图所示,
,,,
,,,
以点为圆心,的长为半径作弧,
,
△是等边三角形,
,
,
△是等腰三角形,
,
,,
,
故答案为:.
【点评】本题考查扇形的面积,直角三角形的性质等知识,解题的关键是学会用分割法求面积,属于中考常考题型.
12.(2025 同心县模拟)如图,四边形是的内接四边形,,则 130 .
【考点】圆内接四边形的性质
【分析】先根据圆周角定理求出的度数,再由圆内接四边形的性质即可得出结论.
【解答】解:,
.
四边形是圆内接四边形,
.
故答案为:130.
【点评】本题考查的是圆内接四边形的性质,熟知圆内接四边形对角互补是解答此题的关键.
13.(2025 宝应县校级模拟)已知的半径为2,内接于,,则 或 .
【答案】或.
【考点】圆内接四边形的性质;三角形的外接圆与外心;等边三角形的判定与性质
【专题】推理能力
【分析】分点在优弧、劣弧两种情况讨论即可.
【解答】解:如图,
,
是等边三角形,
,
当点在优弧上时,
,
当点在劣弧上时,记为,
,
,
的度数为或.
故答案为:或.
【点评】本题考查三角形的外接圆与外心,等边三角形的判定和性质,圆内接四边形的性质,正确的作出图形是解题的关键.
14.(2025 盐城三模)圆在中式建筑中有着广泛的应用.如图,某园林中圆弧形门洞的顶端到地面的高度为,地面入口的宽度为,门枕的高度为,则该圆弧所在圆的半径为 1.3 .
【考点】垂径定理的应用
【专题】圆的有关概念及性质;推理能力
【分析】设该门洞的半径的半径为 ,过点作于点,延长交圆于点,连接,则,,由垂径定理得,然后在△中,由勾股定理得出方程,解方程即可.
【解答】解:设该门洞的半径的半径为 ,
如图,过点圆心作于点,延长交圆于点,连接,
则,,
,
在△中,由勾股定理得:,
,
解得:,
即该门洞的半径为,
故答案为:1.3.
【点评】本题考查了垂径定理的应用以及勾股定理的应用,掌握垂径定理,由勾股定理得出方程是解题的关键.
15.(2025 济宁二模)如图,在四边形中,,,,,点在线段上运动,点在线段上,,则线段的最小值为 8 .
【答案】8.
【考点】三角形内角和定理;勾股定理;圆周角定理
【专题】解直角三角形及其应用;运算能力;推理能力
【分析】设的中点为,以为直径画圆,连接,设与的交点为点,证明,可知点在以为直径的半圆上运动,当点运动到与的交点时,线段有最小值,据此求解即可.
【解答】解:设的中点为,以为直径画圆,连接,如图,
设与的交点为点,
,
,
,
,
,
点在以为直径的半圆上运动,
当点运动到与的交点时,线段有最小值,
,,
,
,
的最小值为.
故答案为:8.
【点评】本题主要考查了圆周角定理的推论、勾股定理、三角形内角和定理等知识,根据题意分析得到点的运动轨迹是解题的关键.
16.(2025 盱眙县校级模拟)《九章算术》第一章“方田”介绍了扇形面积计算方法,其中这样一道题:“今有宛田,下周三十步,径十六步,问为田几何?”意思是:有一块扇形状的田,弧长为30步,其所在圆的直径是16步,则这块田的面积为 120 平方步.
【考点】弧长的计算;扇形面积的计算
【专题】与圆有关的计算;推理能力
【分析】利用扇形面积公式即可计算的解.
【解答】解:扇形的田,弧长30步,其所在圆的直径是16步,
这块田的面积(平方步),
故答案为:120.
【点评】本题是扇形面积公式的应用,考查了推理能力,是基础题.
17.(2025 东莞市校级二模)如图,的半径为5,弦的长为8,是弦上的一个动点,则线段的长的最小值为 3 .
【答案】3.
【考点】勾股定理;垂径定理
【专题】圆的有关概念及性质;推理能力
【分析】过作,连接,由“过直线外一点与直线上的所有连线中垂线段最短”的知识可知,当于重合时最短,由垂径定理可得出的长,再根据勾股定理可求出的长,即线段长的最小值.
【解答】解:如图所示,过作,连接,
过直线外一点与直线上的所有连线中垂线段最短,
当于重合时最短,
,,
,
在中,,
线段长的最小值为3.
故答案为:3.
【点评】本题考查的是垂径定理,熟知垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.
18.(2025 浙江模拟)如图,正方形的边长为2,以边上的动点为圆心,为半径作圆,将沿翻折至△,若过△一边上的中点,则的半径为 或或 .
【答案】或或.
【考点】翻折变换(折叠问题);正方形的性质;圆周角定理
【专题】推理能力;运算能力;平移、旋转与对称;等腰三角形与直角三角形;矩形 菱形 正方形
【分析】分三种情况进行解答,即当以为半径的过△的边的中点,过△的边的中点,过△的边的中点,分别画出相应的图形,根据折叠的性质,勾股定理列方程求解即可.
【解答】解:如图1,当以为半径的过△的边的中点时,
由折叠可知,而,
,
;
如图2,当以为半径的过△的边的中点时,则,
设,则,,
在中,由勾股定理得,
,
即,
解得或舍去,
即半径;
如图3,当以为半径的过△的边的中点时,则,
设,则,,
在△中,由勾股定理得,
,
即,
解得,
即半径,
综上所述,半径的长为或或.
故答案为:或或.
【点评】本题考查翻折的性质,勾股定理,正方形的性质,掌握翻折的性质,勾股定理,正方形的性质以及分类讨论是正确解答的关键.
19.(2025 金凤区校级二模)如图,、、、为一个正多边形的顶点,为正多边形的中心,若,则这个正多边形的边数为 九 .
【答案】九.
【考点】正多边形和圆
【专题】圆的有关概念及性质;正多边形与圆;运算能力;应用意识
【分析】根据圆周角定理可得正多边形的边所对的圆心角,再根据正多边形的一条边所对的圆心角的度数与边数之间的关系可得答案.
【解答】解:如图,设正多边形的外接圆为,连接,,
,
,
而,
这个正多边形为正九边形,
故答案为:九.
【点评】本题考查正多边形与圆,圆周角,掌握圆周角定理是解决问题的关键,理解正多边形的边数与相应的圆心角之间的关系是解决问题的前提.
20.(2025 佳木斯三模)日常生活中常见的装饰盘由圆盘和支架组成(如图,它可以看作如图2所示的几何图形.已知,,垂足为点,,垂足为点,,的半径,则圆盘离桌面最近的距离是 .
【答案】.
【考点】垂径定理;勾股定理的应用
【专题】等腰三角形与直角三角形;圆的有关概念及性质;推理能力
【分析】连接,,过点作于点,交一点,交于点.利用垂径定理,勾股定理求出,,再求出可得结论.
【解答】解:如图2,连接,,过点作于点,交于点,交于点.
,,
,
,
四边形是平行四边形,
,
四边形是矩形,
,,
,
,
,
,
,
,
,
圆盘离桌面最近的距离是,
故答案为:.
【点评】本题考查垂径定理,勾股定理,矩形的判定和性质等知识,解题的关键是理解题意,学会添加常用辅助线,构造直角三角形解决问题.
三.解答题(共5小题)
21.(2025 绵阳)如图,为△的外接圆,弦,垂足为,直径交于点,连接,.若,.
(1)证明:四边形为平行四边形;
(2)求为值;
(3)求的值.
【答案】(1)见解析;
(2);
(3).
【考点】圆的综合题
【专题】几何综合题;运算能力;推理能力
【分析】(1)根据圆周角定理得到,根据平行线的判定定理得到,推出,得到,根据平行四边形的判定定理得到结论;
(2)设,得到,根据勾股定理得到,,得到,根据相似三角形的判定和性质定理即可得到结论;
(3)过点作于,根据勾股定理得到,根据相似三角形的性质得到,求得,,根据三角函数的定义即可得到结论.
【解答】(1)证明:是的直径,
,
,
,
,
,
,
,
,
,
,
,
,
四边形为平行四边形;
(2)解:设,
,
,
,
,
,
,
,
解得,
,,
,
由(1)知,,
,
△△,
,
;
(3)解:过点作于,
在△中,,
,
,
,
△△,
,
,
,,
,
,
,
,
在△中,,
.
【点评】本题是圆的综合题,考查了三角形外接圆和外心,平行四边形的判定,相似三角形的判定和性质,解直角三角形,圆周角定理,正地的作出辅助线是解题的关键.
22.(2025 凉山州模拟)如图,在△中,,以为直径的交于点,为的中点,连接并延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求长.
【答案】(1)见解析;
(2).
【考点】垂径定理;切线的判定与性质;含30度角的直角三角形;圆周角定理
【专题】推理能力;几何直观;等腰三角形与直角三角形;与圆有关的计算
【分析】(1)连接,,结合圆周角定理和直角三角形斜边中线等于斜边的一半求得,从而可得,然后根据切线的判定定理分析证明;
(2)结合含的直角三角形性质及勾股定理分析计算求解.
【解答】(1)证明:连接,,如图,
是的直径,
,
,
在△中,为的中点,
,
,
,
,
,
,
,
,
即,
为半径,,
是的切线;
(2)解:,
,
在△中,,
,,
设,则,
由勾股定理可得:,即,
解得,
,,
,
同理在△中,设,则,
由勾股定理可得:,即,
解得,即.
【点评】本题考查了切线的判定与性质,圆周角定理,直角三角形的性质及解直角三角形等知识.正确的作出辅助线构造直角三角形是解题的关键.
23.(2025 武威三模)如图,以四边形的对角线为直径作圆,圆心为,过点作的延长线于点,已知平分.
(1)求证:是切线;
(2)若,,求的半径和的长.
【考点】切线的判定与性质;圆周角定理;角平分线的性质
【专题】圆的有关概念及性质;证明题;与圆有关的计算;推理能力;运算能力
【分析】(1)连接,根据已知条件证明即可解决问题;
(2)取中点,连接,根据垂径定理可得,所以四边形是矩形,利用勾股定理即可求出结果.
【解答】(1)证明:如图,连接,
,
.
平分,
,
又,
,
,
,
是切线;
(2)解:如图,取中点,连接,
于点.
四边形是矩形,
,
.
在中,,
,
在中,,,
,
的长是.
【点评】本题考查了切线的判定与性质,垂径定理,圆周角定理,勾股定理,解决本题的关键是掌握切线的判定与性质.
24.(2025 烟台一模)如图,圆内接四边形的对角线,交于点,平分,.
(1)求证:为圆的直径;
(2)过点作交的延长线于点,若,,求此圆半径的长.
【答案】(1)证明见解析;
(2)4.
【考点】圆内接四边形的性质;圆周角定理
【专题】推理能力;与圆有关的计算
【分析】(1)根据同弧所对的圆周角相等,即可得到,根据角平分线的定义得到,根据圆内接四边形对角互补得到,从而证得,根据三角形内角和定理求出,最后根据的圆周角所对的弦是直径即可得证;
(2)先证是等边三角形,即可求出,再根据平行线的性质求出的度数,根据含角的直角三角形的性质得出的长,再在中求出的长,即可得出圆的半径.
【解答】(1)证明:,
又,
,
平分,
,
四边形是圆内接四边形,
,
,
,
即,
,
为圆的直径;
(2)解:平分,
,
,
,
,
,
是等边三角形,
,
,
,
,
,
,
,
,
,
,
,
为直径,
,
,,
,
,
圆的半径长为4.
【点评】本题考查了圆内接四边形的性质,圆周角定理及推论,等边三角形的判定与性质,含角的直角三角形的性质,平行线的性质,涉及的知识点较多,需熟练掌握.
25.(2025 哈尔滨模拟)如图,内接于圆,连接.
(1)如图1,求证:;
(2)如图2,于交圆于,于,求证:;
(3)如图3,在(2)的条件下,若平分,延长交于,,,求长.
【答案】(1)证明见解析;(2)证明见解析;(2).
【考点】圆的综合题
【专题】运算能力;推理能力;圆的有关概念及性质;等腰三角形与直角三角形;图形的全等;图形的相似;矩形 菱形 正方形
【分析】(1)延长,交于点,连接,利用圆周角定理和直角三角形的性质解答即可;
(2)作直径,连接,利用垂径定理和三角形的中位线定理得到;再利用圆周角定理,直角三角形的性质和(1)的结论得到,则,结论可得;
(3)过点作于点,过点作于点,连接,利用矩形的判定与性质,全等三角形的判定与性质得到,利用勾股定理得到,设,则,利用勾股定理求得值,再利用垂径定理和勾股定理解答即可得出结论.
【解答】(1)证明:延长,交于点,连接,如图,
则为的直径,
,
.
,
;
(2)证明:作直径,连接,如图,
,
,
为的直径,
,
,
,
,
为的中位线,
.
由(1)知:,
,
,
,
,
,
,
;
(3)解:过点作于点,过点作于点,连接,如图,
,,,
四边形为矩形,
,.
平分,
.
在和中,
,
,
,.
,
,
由(2)知:,
.
在和中,
,
,
,
,,
,
设,则,
,
,
,
.
,
,
.
,,
,
,
,
,
,
,
.
.
【点评】本题主要考查了圆的有关性质,圆周角定理,垂径定理,直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质,角平分线的定义,勾股定理,三角形的中位线定理,矩形的判定与性质,作出圆的直径构造直角三角形是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十四章 圆
一.选择题(共10小题)
1.(2025 绵阳)如图,在边长为2的正六边形中,连接,点在上运动,点为的中点,当△的周长最小时,
A. B. C.12 D.13
2.(2025 绵阳)将一把折扇展开,可抽象成一个扇形,若该扇形的半径为2,弧长为,则扇形的圆心角大小为
A. B. C. D.
3.(2025 当阳市模拟)已知的半径为5,点在内,则的长可能是
A.7 B.6 C.5 D.4
4.(2025 任城区一模)如图,、是的两条直径,是劣弧的中点,若,则的度数是
A. B. C. D.
5.(2025 高邮市校级模拟)已知的半径是6,点是平面内一点且,则点与的位置关系是
A.圆内 B.圆外 C.圆上 D.无法确定
6.(2025 雁塔区校级四模)如图,四边形内接于,已知点为的中点,若,则的度数为
A. B. C. D.
7.(2025 沙坪坝区校级一模)如图,是的直径,过的延长线上的点作的切线,切点为,点是上一点,连接,,若,则等于
A. B. C. D.
8.(2025 丛台区校级三模)如图,在中,满足,则下列对弦与弦大小关系表述正确的是
A. B. C. D.无法确定
9.(2025 临邑县一模)如图,在矩形中,,以为直径作,将矩形绕点旋转,使所得矩形的边与相切,切点为,边与相交于点.若,则长为
A.9 B.10 C. D.12
10.(2025 南岗区校级二模)如图,是的直径,,,是的弦且,则等于
A. B. C. D.
二.填空题(共10小题)
11.(2025 滕州市一模)如图,在△中,,,,以点为圆心,的长为半径作弧,分别交,于点,,则图中阴影部分的面积为 .
12.(2025 同心县模拟)如图,四边形是的内接四边形,,则 .
13.(2025 宝应县校级模拟)已知的半径为2,内接于,,则 .
14.(2025 盐城三模)圆在中式建筑中有着广泛的应用.如图,某园林中圆弧形门洞的顶端到地面的高度为,地面入口的宽度为,门枕的高度为,则该圆弧所在圆的半径为 .
15.(2025 济宁二模)如图,在四边形中,,,,,点在线段上运动,点在线段上,,则线段的最小值为 .
16.(2025 盱眙县校级模拟)《九章算术》第一章“方田”介绍了扇形面积计算方法,其中这样一道题:“今有宛田,下周三十步,径十六步,问为田几何?”意思是:有一块扇形状的田,弧长为30步,其所在圆的直径是16步,则这块田的面积为 平方步.
17.(2025 东莞市校级二模)如图,的半径为5,弦的长为8,是弦上的一个动点,则线段的长的最小值为 .
18.(2025 浙江模拟)如图,正方形的边长为2,以边上的动点为圆心,为半径作圆,将沿翻折至△,若过△一边上的中点,则的半径为 .
19.(2025 金凤区校级二模)如图,、、、为一个正多边形的顶点,为正多边形的中心,若,则这个正多边形的边数为 .
20.(2025 佳木斯三模)日常生活中常见的装饰盘由圆盘和支架组成(如图,它可以看作如图2所示的几何图形.已知,,垂足为点,,垂足为点,,的半径,则圆盘离桌面最近的距离是 .
三.解答题(共5小题)
21.(2025 绵阳)如图,为△的外接圆,弦,垂足为,直径交于点,连接,.若,.
(1)证明:四边形为平行四边形;
(2)求为值;
(3)求的值.
22.(2025 凉山州模拟)如图,在△中,,以为直径的交于点,为的中点,连接并延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求长.
23.(2025 武威三模)如图,以四边形的对角线为直径作圆,圆心为,过点作的延长线于点,已知平分.
(1)求证:是切线;
(2)若,,求的半径和的长.
24.(2025 烟台一模)如图,圆内接四边形的对角线,交于点,平分,.
(1)求证:为圆的直径;
(2)过点作交的延长线于点,若,,求此圆半径的长.
25.(2025 哈尔滨模拟)如图,内接于圆,连接.
(1)如图1,求证:;
(2)如图2,于交圆于,于,求证:;
(3)如图3,在(2)的条件下,若平分,延长交于,,,求长.
第二十四章 圆
参考答案与试题解析
一.选择题(共10小题)
1.(2025 绵阳)如图,在边长为2的正六边形中,连接,点在上运动,点为的中点,当△的周长最小时,
A. B. C.12 D.13
【答案】
【考点】轴对称最短路线问题;正多边形和圆
【专题】运算能力;多边形与平行四边形
【分析】要使△的周长最小时,最小,利用正六边形的性质可得点关于的对称点为点,连接交于点,连接,,那么有,最小,再根据正六边形的性质和勾股定理计算即可.
【解答】解:如图,
要使△的周长的最小,即最小,
利用正六边形的性质可得点关于的对称点为点,连接交于点,连接,,
那么有,最小,
,,
,
,,
,
故当△的周长最小时,.
故选:.
【点评】此题主要考查了正多边形和圆以及轴对称最短路线问题,得出点位置是解题关键.
2.(2025 绵阳)将一把折扇展开,可抽象成一个扇形,若该扇形的半径为2,弧长为,则扇形的圆心角大小为
A. B. C. D.
【答案】
【考点】弧长的计算
【专题】运算能力;与圆有关的计算
【分析】依据题意,根据弧长公式进行代入计算即可得解.
【解答】解:由题意,弧长,且,
.
故选:.
【点评】本题主要考查了弧长的计算,解题时要能熟练掌握并能准确计算是关键.
3.(2025 当阳市模拟)已知的半径为5,点在内,则的长可能是
A.7 B.6 C.5 D.4
【答案】
【考点】点与圆的位置关系
【专题】与圆有关的位置关系;推理能力
【分析】根据点在圆内,点到圆心的距离小于圆的半径进行判断.
【解答】解:的半径为5,点在内,
.
故选:.
【点评】本题考查了点与圆的位置关系:设的半径为,点到圆心的距离,则有:点在圆外;点在圆上;点在圆内.
4.(2025 任城区一模)如图,、是的两条直径,是劣弧的中点,若,则的度数是
A. B. C. D.
【答案】
【考点】圆心角、弧、弦的关系;圆周角定理
【专题】与圆有关的计算;推理能力
【分析】首先根据“同弧或等弧所对的弦长相等,对的圆心角也相等”求得,再根据等腰三角形“等边对等角”的性质求解即可.
【解答】解:如图,连接,
是劣弧的中点,
即弧弧,
,
,
,
,
,
即.
故选:.
【点评】本题主要考查了弧与圆心角的关系、等腰三角形的性质、三角形内角和定理等知识,熟练掌握相关知识并灵活运用是解题关键.
5.(2025 高邮市校级模拟)已知的半径是6,点是平面内一点且,则点与的位置关系是
A.圆内 B.圆外 C.圆上 D.无法确定
【答案】
【考点】点与圆的位置关系
【专题】与圆有关的位置关系;推理能力
【分析】根据点与圆的位置关系的判定方法对点与的位置关系进行判断即可.
【解答】解:的半径为6,,
点到圆心的距离大于圆的半径,
点在外.
故选:.
【点评】本题考查了点与圆的位置关系,熟知设的半径为,点到圆心的距离,则点在圆外;点在圆上;点在圆内是解题的关键.
6.(2025 雁塔区校级四模)如图,四边形内接于,已知点为的中点,若,则的度数为
A. B. C. D.
【答案】
【考点】圆心角、弧、弦的关系;圆周角定理;圆内接四边形的性质
【专题】推理能力;圆的有关概念及性质
【分析】根据圆内接四边形的性质得到,根据等腰三角形的性质即可得到结论.
【解答】解:四边形内接于,,
,
点为的中点,
,
,
故选:.
【点评】本题考查的是圆内接四边形的性质,圆心角、弧、弦的关系、圆周角定理的应用,掌握圆心角、弧、弦的关系定理和圆周角定理是解题的关键.
7.(2025 沙坪坝区校级一模)如图,是的直径,过的延长线上的点作的切线,切点为,点是上一点,连接,,若,则等于
A. B. C. D.
【答案】
【考点】圆周角定理;切线的性质
【专题】与圆有关的位置关系;推理能力
【分析】连接,如图,先根据切线的性质得到,再根据圆周角定理得到,然后利用互余可表示出.
【解答】解:连接,如图,
为的切线,
,
,
,
.
故选:.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理.
8.(2025 丛台区校级三模)如图,在中,满足,则下列对弦与弦大小关系表述正确的是
A. B. C. D.无法确定
【答案】
【考点】三角形三边关系;圆心角、弧、弦的关系
【专题】圆的有关概念及性质;推理能力
【分析】如图,取弧的中点,连接,.证明,再利用三角形的三边关系解决问题.
【解答】解:如图,取弧的中点,连接,.
,,
,
,
,
.
故选:.
【点评】本题考查圆心角,弧,弦之间等分关系,三角形的三边关系等知识,解题的关键是理解题意正确作出辅助线.
9.(2025 临邑县一模)如图,在矩形中,,以为直径作,将矩形绕点旋转,使所得矩形的边与相切,切点为,边与相交于点.若,则长为
A.9 B.10 C. D.12
【答案】
【考点】圆周角定理;矩形的性质;切线的判定与性质;旋转的性质
【专题】平移、旋转与对称;矩形 菱形 正方形;计算题;运算能力;推理能力
【分析】连接,延长交于点,设,则,由勾股定理得出,解得,则得出答案.
【解答】解:连接,延长交于点,
与相切,
,
又矩形中,,
,
,
矩形绕点旋转所得矩形为,
,,,
四边形为矩形,
,
设,则,
,
,
解得,
.
故选:.
【点评】本题主要考查圆的切线的判定与性质,解题的关键是掌握矩形的判定与性质、旋转的性质、切线的性质、垂径定理等知识点.
10.(2025 南岗区校级二模)如图,是的直径,,,是的弦且,则等于
A. B. C. D.
【答案】
【考点】圆心角、弧、弦的关系;圆周角定理
【专题】圆的有关概念及性质;推理能力
【分析】由已知可得,弦、、三等分半圆,从而不难求得的度数.
【解答】解:连接、,
,
,
弦、、三等分半圆,
弦和和对的圆心角均为,
.
故选:.
【点评】本题利用了弧、弦与圆心角的关系求解,注意半圆对的圆心角为.
二.填空题(共10小题)
11.(2025 滕州市一模)如图,在△中,,,,以点为圆心,的长为半径作弧,分别交,于点,,则图中阴影部分的面积为 .
【考点】含30度角的直角三角形;扇形面积的计算
【专题】与圆有关的计算;应用意识
【分析】连接,过点作,垂足为,找出即可求出答案.
【解答】解:连接,过点作,垂足为,如图所示,
,,,
,,,
以点为圆心,的长为半径作弧,
,
△是等边三角形,
,
,
△是等腰三角形,
,
,,
,
故答案为:.
【点评】本题考查扇形的面积,直角三角形的性质等知识,解题的关键是学会用分割法求面积,属于中考常考题型.
12.(2025 同心县模拟)如图,四边形是的内接四边形,,则 130 .
【考点】圆内接四边形的性质
【分析】先根据圆周角定理求出的度数,再由圆内接四边形的性质即可得出结论.
【解答】解:,
.
四边形是圆内接四边形,
.
故答案为:130.
【点评】本题考查的是圆内接四边形的性质,熟知圆内接四边形对角互补是解答此题的关键.
13.(2025 宝应县校级模拟)已知的半径为2,内接于,,则 或 .
【答案】或.
【考点】圆内接四边形的性质;三角形的外接圆与外心;等边三角形的判定与性质
【专题】推理能力
【分析】分点在优弧、劣弧两种情况讨论即可.
【解答】解:如图,
,
是等边三角形,
,
当点在优弧上时,
,
当点在劣弧上时,记为,
,
,
的度数为或.
故答案为:或.
【点评】本题考查三角形的外接圆与外心,等边三角形的判定和性质,圆内接四边形的性质,正确的作出图形是解题的关键.
14.(2025 盐城三模)圆在中式建筑中有着广泛的应用.如图,某园林中圆弧形门洞的顶端到地面的高度为,地面入口的宽度为,门枕的高度为,则该圆弧所在圆的半径为 1.3 .
【考点】垂径定理的应用
【专题】圆的有关概念及性质;推理能力
【分析】设该门洞的半径的半径为 ,过点作于点,延长交圆于点,连接,则,,由垂径定理得,然后在△中,由勾股定理得出方程,解方程即可.
【解答】解:设该门洞的半径的半径为 ,
如图,过点圆心作于点,延长交圆于点,连接,
则,,
,
在△中,由勾股定理得:,
,
解得:,
即该门洞的半径为,
故答案为:1.3.
【点评】本题考查了垂径定理的应用以及勾股定理的应用,掌握垂径定理,由勾股定理得出方程是解题的关键.
15.(2025 济宁二模)如图,在四边形中,,,,,点在线段上运动,点在线段上,,则线段的最小值为 8 .
【答案】8.
【考点】三角形内角和定理;勾股定理;圆周角定理
【专题】解直角三角形及其应用;运算能力;推理能力
【分析】设的中点为,以为直径画圆,连接,设与的交点为点,证明,可知点在以为直径的半圆上运动,当点运动到与的交点时,线段有最小值,据此求解即可.
【解答】解:设的中点为,以为直径画圆,连接,如图,
设与的交点为点,
,
,
,
,
,
点在以为直径的半圆上运动,
当点运动到与的交点时,线段有最小值,
,,
,
,
的最小值为.
故答案为:8.
【点评】本题主要考查了圆周角定理的推论、勾股定理、三角形内角和定理等知识,根据题意分析得到点的运动轨迹是解题的关键.
16.(2025 盱眙县校级模拟)《九章算术》第一章“方田”介绍了扇形面积计算方法,其中这样一道题:“今有宛田,下周三十步,径十六步,问为田几何?”意思是:有一块扇形状的田,弧长为30步,其所在圆的直径是16步,则这块田的面积为 120 平方步.
【考点】弧长的计算;扇形面积的计算
【专题】与圆有关的计算;推理能力
【分析】利用扇形面积公式即可计算的解.
【解答】解:扇形的田,弧长30步,其所在圆的直径是16步,
这块田的面积(平方步),
故答案为:120.
【点评】本题是扇形面积公式的应用,考查了推理能力,是基础题.
17.(2025 东莞市校级二模)如图,的半径为5,弦的长为8,是弦上的一个动点,则线段的长的最小值为 3 .
【答案】3.
【考点】勾股定理;垂径定理
【专题】圆的有关概念及性质;推理能力
【分析】过作,连接,由“过直线外一点与直线上的所有连线中垂线段最短”的知识可知,当于重合时最短,由垂径定理可得出的长,再根据勾股定理可求出的长,即线段长的最小值.
【解答】解:如图所示,过作,连接,
过直线外一点与直线上的所有连线中垂线段最短,
当于重合时最短,
,,
,
在中,,
线段长的最小值为3.
故答案为:3.
【点评】本题考查的是垂径定理,熟知垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.
18.(2025 浙江模拟)如图,正方形的边长为2,以边上的动点为圆心,为半径作圆,将沿翻折至△,若过△一边上的中点,则的半径为 或或 .
【答案】或或.
【考点】翻折变换(折叠问题);正方形的性质;圆周角定理
【专题】推理能力;运算能力;平移、旋转与对称;等腰三角形与直角三角形;矩形 菱形 正方形
【分析】分三种情况进行解答,即当以为半径的过△的边的中点,过△的边的中点,过△的边的中点,分别画出相应的图形,根据折叠的性质,勾股定理列方程求解即可.
【解答】解:如图1,当以为半径的过△的边的中点时,
由折叠可知,而,
,
;
如图2,当以为半径的过△的边的中点时,则,
设,则,,
在中,由勾股定理得,
,
即,
解得或舍去,
即半径;
如图3,当以为半径的过△的边的中点时,则,
设,则,,
在△中,由勾股定理得,
,
即,
解得,
即半径,
综上所述,半径的长为或或.
故答案为:或或.
【点评】本题考查翻折的性质,勾股定理,正方形的性质,掌握翻折的性质,勾股定理,正方形的性质以及分类讨论是正确解答的关键.
19.(2025 金凤区校级二模)如图,、、、为一个正多边形的顶点,为正多边形的中心,若,则这个正多边形的边数为 九 .
【答案】九.
【考点】正多边形和圆
【专题】圆的有关概念及性质;正多边形与圆;运算能力;应用意识
【分析】根据圆周角定理可得正多边形的边所对的圆心角,再根据正多边形的一条边所对的圆心角的度数与边数之间的关系可得答案.
【解答】解:如图,设正多边形的外接圆为,连接,,
,
,
而,
这个正多边形为正九边形,
故答案为:九.
【点评】本题考查正多边形与圆,圆周角,掌握圆周角定理是解决问题的关键,理解正多边形的边数与相应的圆心角之间的关系是解决问题的前提.
20.(2025 佳木斯三模)日常生活中常见的装饰盘由圆盘和支架组成(如图,它可以看作如图2所示的几何图形.已知,,垂足为点,,垂足为点,,的半径,则圆盘离桌面最近的距离是 .
【答案】.
【考点】垂径定理;勾股定理的应用
【专题】等腰三角形与直角三角形;圆的有关概念及性质;推理能力
【分析】连接,,过点作于点,交一点,交于点.利用垂径定理,勾股定理求出,,再求出可得结论.
【解答】解:如图2,连接,,过点作于点,交于点,交于点.
,,
,
,
四边形是平行四边形,
,
四边形是矩形,
,,
,
,
,
,
,
,
,
圆盘离桌面最近的距离是,
故答案为:.
【点评】本题考查垂径定理,勾股定理,矩形的判定和性质等知识,解题的关键是理解题意,学会添加常用辅助线,构造直角三角形解决问题.
三.解答题(共5小题)
21.(2025 绵阳)如图,为△的外接圆,弦,垂足为,直径交于点,连接,.若,.
(1)证明:四边形为平行四边形;
(2)求为值;
(3)求的值.
【答案】(1)见解析;
(2);
(3).
【考点】圆的综合题
【专题】几何综合题;运算能力;推理能力
【分析】(1)根据圆周角定理得到,根据平行线的判定定理得到,推出,得到,根据平行四边形的判定定理得到结论;
(2)设,得到,根据勾股定理得到,,得到,根据相似三角形的判定和性质定理即可得到结论;
(3)过点作于,根据勾股定理得到,根据相似三角形的性质得到,求得,,根据三角函数的定义即可得到结论.
【解答】(1)证明:是的直径,
,
,
,
,
,
,
,
,
,
,
,
,
四边形为平行四边形;
(2)解:设,
,
,
,
,
,
,
,
解得,
,,
,
由(1)知,,
,
△△,
,
;
(3)解:过点作于,
在△中,,
,
,
,
△△,
,
,
,,
,
,
,
,
在△中,,
.
【点评】本题是圆的综合题,考查了三角形外接圆和外心,平行四边形的判定,相似三角形的判定和性质,解直角三角形,圆周角定理,正地的作出辅助线是解题的关键.
22.(2025 凉山州模拟)如图,在△中,,以为直径的交于点,为的中点,连接并延长交的延长线于点.
(1)求证:是的切线;
(2)若,,求长.
【答案】(1)见解析;
(2).
【考点】垂径定理;切线的判定与性质;含30度角的直角三角形;圆周角定理
【专题】推理能力;几何直观;等腰三角形与直角三角形;与圆有关的计算
【分析】(1)连接,,结合圆周角定理和直角三角形斜边中线等于斜边的一半求得,从而可得,然后根据切线的判定定理分析证明;
(2)结合含的直角三角形性质及勾股定理分析计算求解.
【解答】(1)证明:连接,,如图,
是的直径,
,
,
在△中,为的中点,
,
,
,
,
,
,
,
,
即,
为半径,,
是的切线;
(2)解:,
,
在△中,,
,,
设,则,
由勾股定理可得:,即,
解得,
,,
,
同理在△中,设,则,
由勾股定理可得:,即,
解得,即.
【点评】本题考查了切线的判定与性质,圆周角定理,直角三角形的性质及解直角三角形等知识.正确的作出辅助线构造直角三角形是解题的关键.
23.(2025 武威三模)如图,以四边形的对角线为直径作圆,圆心为,过点作的延长线于点,已知平分.
(1)求证:是切线;
(2)若,,求的半径和的长.
【考点】切线的判定与性质;圆周角定理;角平分线的性质
【专题】圆的有关概念及性质;证明题;与圆有关的计算;推理能力;运算能力
【分析】(1)连接,根据已知条件证明即可解决问题;
(2)取中点,连接,根据垂径定理可得,所以四边形是矩形,利用勾股定理即可求出结果.
【解答】(1)证明:如图,连接,
,
.
平分,
,
又,
,
,
,
是切线;
(2)解:如图,取中点,连接,
于点.
四边形是矩形,
,
.
在中,,
,
在中,,,
,
的长是.
【点评】本题考查了切线的判定与性质,垂径定理,圆周角定理,勾股定理,解决本题的关键是掌握切线的判定与性质.
24.(2025 烟台一模)如图,圆内接四边形的对角线,交于点,平分,.
(1)求证:为圆的直径;
(2)过点作交的延长线于点,若,,求此圆半径的长.
【答案】(1)证明见解析;
(2)4.
【考点】圆内接四边形的性质;圆周角定理
【专题】推理能力;与圆有关的计算
【分析】(1)根据同弧所对的圆周角相等,即可得到,根据角平分线的定义得到,根据圆内接四边形对角互补得到,从而证得,根据三角形内角和定理求出,最后根据的圆周角所对的弦是直径即可得证;
(2)先证是等边三角形,即可求出,再根据平行线的性质求出的度数,根据含角的直角三角形的性质得出的长,再在中求出的长,即可得出圆的半径.
【解答】(1)证明:,
又,
,
平分,
,
四边形是圆内接四边形,
,
,
,
即,
,
为圆的直径;
(2)解:平分,
,
,
,
,
,
是等边三角形,
,
,
,
,
,
,
,
,
,
,
,
为直径,
,
,,
,
,
圆的半径长为4.
【点评】本题考查了圆内接四边形的性质,圆周角定理及推论,等边三角形的判定与性质,含角的直角三角形的性质,平行线的性质,涉及的知识点较多,需熟练掌握.
25.(2025 哈尔滨模拟)如图,内接于圆,连接.
(1)如图1,求证:;
(2)如图2,于交圆于,于,求证:;
(3)如图3,在(2)的条件下,若平分,延长交于,,,求长.
【答案】(1)证明见解析;(2)证明见解析;(2).
【考点】圆的综合题
【专题】运算能力;推理能力;圆的有关概念及性质;等腰三角形与直角三角形;图形的全等;图形的相似;矩形 菱形 正方形
【分析】(1)延长,交于点,连接,利用圆周角定理和直角三角形的性质解答即可;
(2)作直径,连接,利用垂径定理和三角形的中位线定理得到;再利用圆周角定理,直角三角形的性质和(1)的结论得到,则,结论可得;
(3)过点作于点,过点作于点,连接,利用矩形的判定与性质,全等三角形的判定与性质得到,利用勾股定理得到,设,则,利用勾股定理求得值,再利用垂径定理和勾股定理解答即可得出结论.
【解答】(1)证明:延长,交于点,连接,如图,
则为的直径,
,
.
,
;
(2)证明:作直径,连接,如图,
,
,
为的直径,
,
,
,
,
为的中位线,
.
由(1)知:,
,
,
,
,
,
,
;
(3)解:过点作于点,过点作于点,连接,如图,
,,,
四边形为矩形,
,.
平分,
.
在和中,
,
,
,.
,
,
由(2)知:,
.
在和中,
,
,
,
,,
,
设,则,
,
,
,
.
,
,
.
,,
,
,
,
,
,
,
.
.
【点评】本题主要考查了圆的有关性质,圆周角定理,垂径定理,直角三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质,角平分线的定义,勾股定理,三角形的中位线定理,矩形的判定与性质,作出圆的直径构造直角三角形是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
