(暑假冲A卷)期末巩固练习(一)(含解析)-数学七年级下册苏科版(2024)
文档属性
| 名称 | (暑假冲A卷)期末巩固练习(一)(含解析)-数学七年级下册苏科版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 788.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 07:35:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
(暑假冲A卷)期末巩固练习(一)-数学七年级下册苏科版(2024)
一、单选题
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.计算的结果是( )
A. B. C. D.
3.我们定义:,若,则的值为( )
A.4 B.16 C.64 D.256
4.若,下列结论中成立的是( )
A. B. C. D.
5.若关于x,y方程组有无数组解,则a与b的值分别是( )
A., B.,
C., D.,
6.下列命题是假命题的是( )
A.同位角相等 B.直角都相等
C.对顶角相等 D.同角的补角相等
7.在数轴上正确表示不等式组的解集的是( )
A. B.
C. D.
8.已知,则的值为( )
A.4 B.6 C.2 D.8
9.我国民间流传这样一道数学名题:
其大意是: 听见隔壁一些人在分银两,每人7两还缺7两,每人半斤则多半斤,问共有多少人?共有多少两银子? 数学原题: 只闻隔壁人分银,不知多少银和人,每人7两还缺7两,每人半斤多半斤,试问各位善算者,多少人分多 少银?(1斤等于10两)
设有个人,共分两银子,根据题意,可列方程组为( )
A. B. C. D.
10.如图,将沿方向平移一定距离得到,点D落在线段上,与交于点G,则下列结论:①;②;③;④;⑤;⑥.其中正确的结论个数是( )
A.3 B.4 C.5 D.6
二、填空题
11.写出命题“两个全等三角形的面积相等”的逆命题 .
12.请写一个解为 的二元一次方程 .
13.若,,则 .
14.若关于的不等式组的解集为,且关于的方程有非负整数解,则符合条件的整数的和是 .
15.每年的6月5日为世界环境日,为了提倡低碳环保,某公司决定购买节省能源的新设备,某种新设备为每套3万元,凡购买两套及以上的新设备,厂家推出两种优惠方案,第一种:一套设备按原价,其余的按原价的七五折优惠;第二种:全部按原价的八折销售.若该公司在购买相同数量新设备的情况下,要使第一种方案得到的优惠多,至少需要购买新设备 套.
16.如图,将绕点按逆时针方向旋转得到.若,则 .
17.关于x的方程的解是非负整数,且关于y的不等式组有且仅有3个整数解,则满足条件的所有整数a的和为 .
三、解答题
18.解方程组:.
19.解不等式组,并将解集表示在数轴上;
20.计算:
(1).
(2)
21.某非遗皮影制作工坊可制作传统人物皮影和动物皮影.已知制作3个传统人物皮影和2个动物皮影共需牛皮12平方分米,制作2个传统人物皮影和3个动物皮影共需牛皮13平方分米.
(1)求制作一个传统人物皮影和一个动物皮影分别需要牛皮多少平方分米?
(2)若该工坊计划用不超过50平方分米的牛皮制作两种皮影共20个,则最少制作传统人物皮影多少个?
22.已知关于x、y的二元一次方程组的解是正数.
(1)用含m的代数式表示方程组的解;
(2)求m的取值范围;
(3)关于z的一元一次方程的解是整数,求整数m的值.
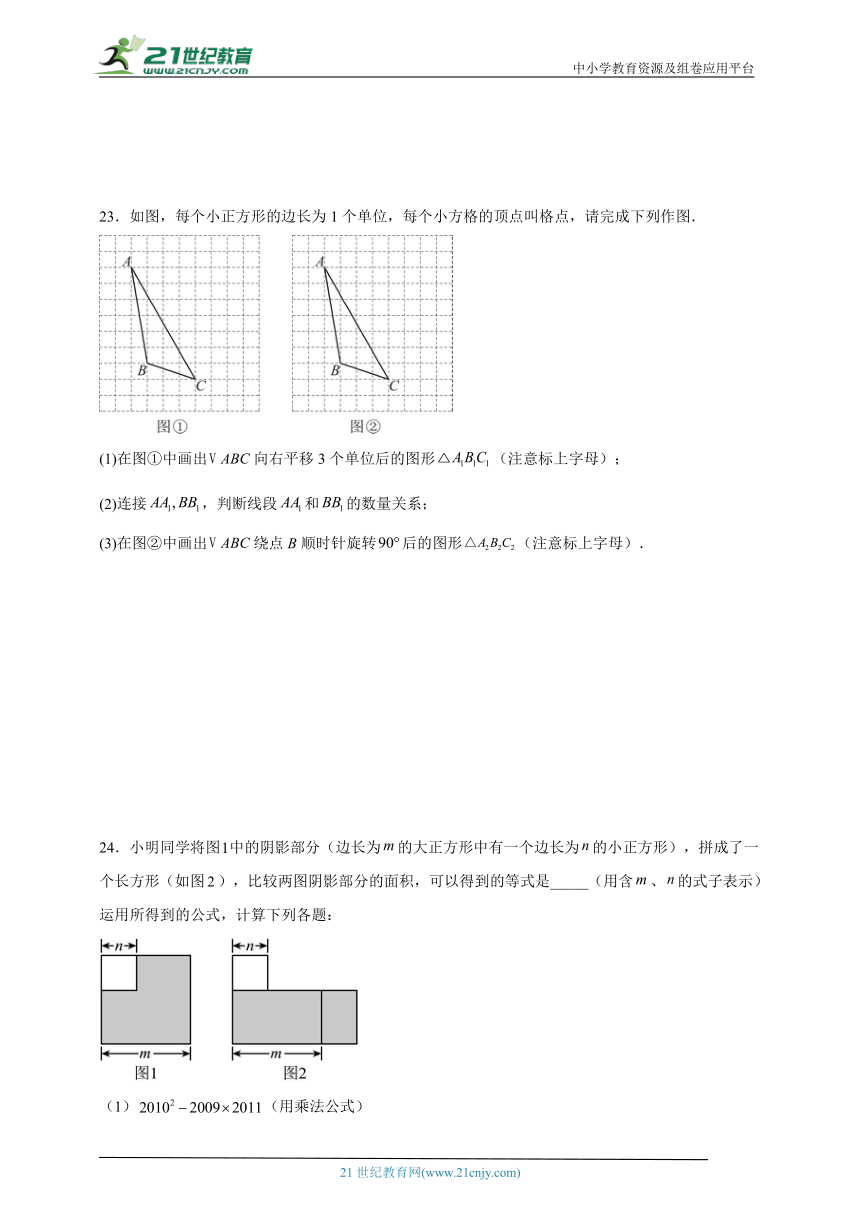
23.如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点,请完成下列作图.
(1)在图①中画出向右平移3个单位后的图形(注意标上字母);
(2)连接,判断线段和的数量关系;
(3)在图②中画出绕点B顺时针旋转后的图形(注意标上字母).
24.小明同学将图中的阴影部分(边长为的大正方形中有一个边长为的小正方形),拼成了一个长方形(如图),比较两图阴影部分的面积,可以得到的等式是_____(用含、的式子表示)运用所得到的公式,计算下列各题:
(1)(用乘法公式)
(2)
25.庙会,又称 “庙市” 或 “节场”,是中国传统民俗文化活动的重要组成部分,具有深厚的历史文化底蕴和浓郁的地方特色.庙会上不仅有丰富多彩的文化活动,在市集上还有各类文创商品.已知2个绢布扇和3个手账本需花费90元;3个绢布扇和4个手账本需花费125元.
(1)绢布扇和手账本的单价分别是多少元?(列方程组解答)
(2)某商店为吸引游客,推出了投壶小游戏,凡购买一件文创商品可获得一次投壶机会,投中1次即可免费赠送一个文创书签.一名游客恰好用110元购买了绢布扇和手账本两种文创商品,问该游客分别购买多少个绢布扇和手账本获得的投壶机会最多?
《(暑假冲A卷)期末巩固练习(一)-数学七年级下册苏科版(2024)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C B D A C C D C
1.D
【分析】本题主要考查了轴对称图形和中心对称图形,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
根据中心对称图形的定义和轴对称图形的定义进行逐项判断即可.
【详解】解:A.是轴对称图形,但不是中心对称图形,不符合题意;
B.不是轴对称图形,是中心对称图形,不符合题意;
C.是轴对称图形,但不是中心对称图形,不符合题意;
D.是轴对称图形,是中心对称图形,符合题意.
故选D.
2.D
【分析】本题考查同底数幂乘法,熟练掌握其运算法则是解题的关键.
利用同底数幂乘法法则计算即可.
【详解】解:,
故选:D.
3.C
【分析】本题考查了整式的混合运算、有理数的混合运算,解决本题的关键是求出.
由定义可得,,.
【详解】
解:因为,
所以,
所以,
因为,
所以
故选:C.
4.B
【分析】本题主要考查了不等式的基本性质,即不等式两边同时加或减去同一个整式,不等号的方向不变;不等式两边同时乘以或除以同一个大于的整式,不等号的方向不变;不等式两边同时乘以或除以同一个小于的整式,不等号的方向改变,熟练掌握不等式的基本性质是解题关键.
根据不等式的基本性质,逐一分析各选项即可.
【详解】解:A、根据题意,可得,即,故此选项不成立,不符合题意;
B、根据题意,可得,故此选项成立,符合题意;
C、根据题意,可得,故此选项不成立,不符合题意;
D、根据题意,可得,故此选项不成立,不符合题意.
故选:B.
5.D
【分析】本题考查了二元一次方程组的解,关键是要理解方程组有无数组解的含义.由关于x,y的方程组有无数组解,求出关于a,b的等式,再根据题意判断即可.
【详解】解∶
,得,
∵方程组有无数组解,
∴,,
∴,,
故选∶D.
6.A
【分析】本题考查几何命题的真假判断,需逐一分析各选项是否符合相关定理或定义,熟练掌握同位角的定义、直角的定义、对顶角的定义以及补角的定义是解此题的关键.
【详解】解:A、同位角相等:只有当两直线平行时,同位角才相等;若两直线不平行,同位角不一定相等;因此该命题缺少前提条件,是假命题,符合题意;
B、直角都相等:直角均为,度数固定,故所有直角都相等,为真命题,故不符合题意;
C、对顶角相等:根据对顶角定理,对顶角一定相等,为真命题,故不符合题意;
D、同角的补角相等:同一个角的补角均为减去该角,度数相同,故相等,为真命题,故不符合题意;
故选:A.
7.C
【分析】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.需要注意的是:如果是表示大于或小于号的点要用空心圆圈,如果是表示大于等于或小于等于号的点要用实心圆点.分别求解两个不等式,得到不等式组的解集,然后判断即可.
【详解】解:
解不等式①得:,
∴不等式组的解集为:,
∴表示在数轴上为:
故选:C.
8.C
【分析】本题考查了换元代入法求代数式的值.通过变量替换简化方程,利用完全平方公式求出,再利用平方差公式求解.
【详解】解:设,则
代入原方程得:,
整理得:,
所求表达式为:,
故选:C.
9.D
【分析】本题主要考查二元一次方程组的运用,理解数量关系是关键,根据题意,每人分7两缺7两,每人分5两多5两,建立方程组即可.
【详解】解:设共有人,两银子,
∵总需银两为,实际银两比所需少7两,
∴,
∵总需银两为,实际银两比所需多5两,
∴,
联立方程得:,
故选:D.
10.C
【分析】本题考查了平移的性质,根据平移的性质逐项分析即可得解,熟练掌握平移的性质是解此题的关键.
【详解】解:由平移的性质可得:,,,,,故①②③④正确,
∴,
∴,即,故⑥正确;
由已知条件不能说明,故⑤错误;
综上所述,正确的有个,
故选:C.
11.两个三角形面积相等则这两个三角形全等
【分析】本题考查了命题的逆命题,掌握逆命题的书写方法是关键.
对于两个命题,如果一个命题的条件和结论分别是另外一个命题的结论和条件,那么这两个命题叫做互逆命题,确定条件和结论,根据逆命题的书写方法即可求解.
【详解】解:“两个全等三角形的面积相等”的条件是“两个三角形全等”,结论是“这两个三角形的面积相等”,
∴逆命题为:两个三角形面积相等则这两个三角形全等,
故答案为:两个三角形面积相等则这两个三角形全等 .
12.(答案不唯一)
【分析】本题考查了二次一次方程组的定义和二元一次方程组的解,能熟记二元一次方程组的定义是解此题的关键.
此题是一道开放型的题目,答案不唯一,只要根据二次一次方程组的定义和二元一次方程组的解写出一个方程组即可.
【详解】解:解为的二元一次方程有.
故答案为:(答案不唯一).
13.
【分析】本题考查了同底数幂乘法的逆运算,利用同底数幂乘法的逆运算计算即可,掌握同底数幂乘法的逆运算是解题的关键.
【详解】解:∵,,
∴,
故答案为:.
14.
【分析】本题主要考查解一元一次不等式组和一元一次方程的整数值,解不等式组,结合其解集得出,解方程得出其解,结合解均为非负整数得出,综合前面的取值范围确定的最终取值,从而得出答案.
【详解】解:,
解不等式①得,
解不等式②得,
∵不等式的解集为,
,即,
解方程得,
∵方程有非负整数解,
,即,
应为偶数,即应为奇数,
符合条件的整数为,,,,
即符合条件的整数的和是.
故答案为:.
15.6
【分析】此题主要考查了一元一次不等式的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.设购买x套新设备第一种办法比第二种办法得到的更优惠,构建不等式求解即可.
【详解】解:设购买x套新设备第一种办法比第二种办法得到的更优惠.由题意得:
,
解得:.
故至少需要购买6套新设备.
故答案为:6.
16.80
【分析】本题考查旋转的性质,由旋转得,再根据可得答案.
【详解】解:由旋转得,,
∵,
∴.
故答案为:80.
17.8
【分析】本题主要考查了一元一次不等式组的整数解及一元一次方程的解,先根据所给方程的解为非负整数,得出a的取值范围,再结合所给不等式组的整数解只有3个即可解决问题.
【详解】解:由方程得,,
因为关于x的方程的解是非负整数,
所以,
解得,
解不等式组得,,
因为此不等式组有且仅有3个整数解,
所以,
解得,
∵为整数,
∴或5,
所以符合条件的所有整数a的和是:.
故答案为:8.
18.
【分析】本题考查解二元一次方程组,根据代入消元法解方程组即可求解.
【详解】解:,
由①得,③
把③代入②,得,
解这个方程,得,
把代入③,得,
所以这个方程组的解是.
19.,将解集表示在数轴上见解析
【分析】本题考查了解一元一次不等式组.也考查了在数轴上表示不等式的解集.分别解两个不等式,再根据大于小的小于大的取中间确定不等式组的解集,然后用数轴表示解集.
【详解】解:解不等式得,
解不等式得,
则不等式组的解集为,
解集在数轴上表示如解图所示.
.
20.(1)
(2)
【分析】本题考查了整式的运算,熟练掌握单项式乘以多项式,幂的运算是解题的关键;
(1)利用单项式乘以多项式的运算法则求解即可;
(2)根据零指数幂,有理数的乘方以及负整数指数幂进行计算即可求解.
【详解】(1)解:
(2)
21.(1)制作一个传统人物皮影需牛皮2平方分米,制作一个动物皮影需牛皮3平方分米
(2)10个
【分析】本题考查二元一次方程组、一元一次不等式解应用题,读懂题意,准确列出方程组及不等式求解是解决问题的关键.
(1)设制作一个传统人物皮影需平方分米的牛皮,制作一个动物皮影需平方分米的牛皮,读懂题意,找准等量关系列二元一次方程组求解即可得到答案;
(2)设制作传统人物皮影个,则制作动物皮影个,读懂题意,列出一元一次不等式求解即可得到答案.
【详解】(1)解:设制作一个传统人物皮影需平方分米的牛皮,制作一个动物皮影需平方分米的牛皮,
由题意得:,
解得,
答:制作一个传统人物皮影需牛皮2平方分米,制作一个动物皮影需牛皮3平分米;
(2)解:设制作传统人物皮影个,则制作动物皮影个,
由题意得,
解得,
答:最少可制作传统人物皮影10个.
22.(1)
(2)
(3)或2
【分析】本题考查的是方程组与不等式组的综合应用,一元一次方程的整数解问题;
(1)利用加减消元法先求解,再求解即可;
(2)由方程的解为正数可得,再解不等式组即可;
(3)由得,,结合方程的解是整数,且m也是整数,,再进一步解答即可.
【详解】(1)解:
由①②得,
∴,
将代入②得,
∴,
∴;
(2)解:∵
∴,
解得;
(3)解:由得,,
∵方程的解是整数,且m也是整数,
∴,
即,
又因为,
∴或2.
23.(1)见解析
(2)
(3)见解析
【分析】本题主要考查了画平移图形,画旋转图形,平移的性质,熟知相关知识是解题的关键.
(1)根据平移方式找到的位置,描出,并顺次连接即可;
(2)由平移的性质即可得到答案;
(3)根据旋转方式和网格的特点找到的位置,描出,并顺次连接即可.
【详解】(1)解:如图所示,即为所求;
(2)解:由平移的性质可得.
(3)解:如图所示,即为所求.
24.;();().
【分析】本题考查了平方差公式的几何图形,完全平方公式,表示图中阴影部分面积是解题的关键.
根据题意分别求出图与图阴影部分面积,然后由面积相等即可求解;
()利用平方差公式即可求解;
()利用平方差公式和完全平方公式即可求解.
【详解】解:图阴影面积:,图阴影面积:,
∵图与图阴影部分面积相等,
∴,
故答案为:;
()
;
()
.
25.(1)绢布扇的单价是15元,手账本的单价是20元
(2)购买6个绢布扇,1个手账本时,获得的投壶机会最多
【分析】本题主要考查了二元一次方程组的实际应用,根据题意,正确列方程或方程组是解题的关键;
(1)设绢布扇的单价是x元,手账本的单价是y元,根据题意列出方程组求解即可;
(2)设购买m个绢布扇,n个手账本,根据题意列出方程,求出m、n的值,再求出的最大值即可得到结论.
【详解】(1)设绢布扇的单价是x元,手账本的单价是y元.
根据题意,得,
解得,
答:绢布扇的单价是15元,手账本的单价是20元;
(2)设购买m个绢布扇,n个手账本.
根据题意,得.
,
又m,n均为正整数,
或,
或,,
购买一件文创商品可获得一次投壶机会,
购买6个绢布扇,1个手账本时,获得的投壶机会最多.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
(暑假冲A卷)期末巩固练习(一)-数学七年级下册苏科版(2024)
一、单选题
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
2.计算的结果是( )
A. B. C. D.
3.我们定义:,若,则的值为( )
A.4 B.16 C.64 D.256
4.若,下列结论中成立的是( )
A. B. C. D.
5.若关于x,y方程组有无数组解,则a与b的值分别是( )
A., B.,
C., D.,
6.下列命题是假命题的是( )
A.同位角相等 B.直角都相等
C.对顶角相等 D.同角的补角相等
7.在数轴上正确表示不等式组的解集的是( )
A. B.
C. D.
8.已知,则的值为( )
A.4 B.6 C.2 D.8
9.我国民间流传这样一道数学名题:
其大意是: 听见隔壁一些人在分银两,每人7两还缺7两,每人半斤则多半斤,问共有多少人?共有多少两银子? 数学原题: 只闻隔壁人分银,不知多少银和人,每人7两还缺7两,每人半斤多半斤,试问各位善算者,多少人分多 少银?(1斤等于10两)
设有个人,共分两银子,根据题意,可列方程组为( )
A. B. C. D.
10.如图,将沿方向平移一定距离得到,点D落在线段上,与交于点G,则下列结论:①;②;③;④;⑤;⑥.其中正确的结论个数是( )
A.3 B.4 C.5 D.6
二、填空题
11.写出命题“两个全等三角形的面积相等”的逆命题 .
12.请写一个解为 的二元一次方程 .
13.若,,则 .
14.若关于的不等式组的解集为,且关于的方程有非负整数解,则符合条件的整数的和是 .
15.每年的6月5日为世界环境日,为了提倡低碳环保,某公司决定购买节省能源的新设备,某种新设备为每套3万元,凡购买两套及以上的新设备,厂家推出两种优惠方案,第一种:一套设备按原价,其余的按原价的七五折优惠;第二种:全部按原价的八折销售.若该公司在购买相同数量新设备的情况下,要使第一种方案得到的优惠多,至少需要购买新设备 套.
16.如图,将绕点按逆时针方向旋转得到.若,则 .
17.关于x的方程的解是非负整数,且关于y的不等式组有且仅有3个整数解,则满足条件的所有整数a的和为 .
三、解答题
18.解方程组:.
19.解不等式组,并将解集表示在数轴上;
20.计算:
(1).
(2)
21.某非遗皮影制作工坊可制作传统人物皮影和动物皮影.已知制作3个传统人物皮影和2个动物皮影共需牛皮12平方分米,制作2个传统人物皮影和3个动物皮影共需牛皮13平方分米.
(1)求制作一个传统人物皮影和一个动物皮影分别需要牛皮多少平方分米?
(2)若该工坊计划用不超过50平方分米的牛皮制作两种皮影共20个,则最少制作传统人物皮影多少个?
22.已知关于x、y的二元一次方程组的解是正数.
(1)用含m的代数式表示方程组的解;
(2)求m的取值范围;
(3)关于z的一元一次方程的解是整数,求整数m的值.
23.如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点,请完成下列作图.
(1)在图①中画出向右平移3个单位后的图形(注意标上字母);
(2)连接,判断线段和的数量关系;
(3)在图②中画出绕点B顺时针旋转后的图形(注意标上字母).
24.小明同学将图中的阴影部分(边长为的大正方形中有一个边长为的小正方形),拼成了一个长方形(如图),比较两图阴影部分的面积,可以得到的等式是_____(用含、的式子表示)运用所得到的公式,计算下列各题:
(1)(用乘法公式)
(2)
25.庙会,又称 “庙市” 或 “节场”,是中国传统民俗文化活动的重要组成部分,具有深厚的历史文化底蕴和浓郁的地方特色.庙会上不仅有丰富多彩的文化活动,在市集上还有各类文创商品.已知2个绢布扇和3个手账本需花费90元;3个绢布扇和4个手账本需花费125元.
(1)绢布扇和手账本的单价分别是多少元?(列方程组解答)
(2)某商店为吸引游客,推出了投壶小游戏,凡购买一件文创商品可获得一次投壶机会,投中1次即可免费赠送一个文创书签.一名游客恰好用110元购买了绢布扇和手账本两种文创商品,问该游客分别购买多少个绢布扇和手账本获得的投壶机会最多?
《(暑假冲A卷)期末巩固练习(一)-数学七年级下册苏科版(2024)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C B D A C C D C
1.D
【分析】本题主要考查了轴对称图形和中心对称图形,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
根据中心对称图形的定义和轴对称图形的定义进行逐项判断即可.
【详解】解:A.是轴对称图形,但不是中心对称图形,不符合题意;
B.不是轴对称图形,是中心对称图形,不符合题意;
C.是轴对称图形,但不是中心对称图形,不符合题意;
D.是轴对称图形,是中心对称图形,符合题意.
故选D.
2.D
【分析】本题考查同底数幂乘法,熟练掌握其运算法则是解题的关键.
利用同底数幂乘法法则计算即可.
【详解】解:,
故选:D.
3.C
【分析】本题考查了整式的混合运算、有理数的混合运算,解决本题的关键是求出.
由定义可得,,.
【详解】
解:因为,
所以,
所以,
因为,
所以
故选:C.
4.B
【分析】本题主要考查了不等式的基本性质,即不等式两边同时加或减去同一个整式,不等号的方向不变;不等式两边同时乘以或除以同一个大于的整式,不等号的方向不变;不等式两边同时乘以或除以同一个小于的整式,不等号的方向改变,熟练掌握不等式的基本性质是解题关键.
根据不等式的基本性质,逐一分析各选项即可.
【详解】解:A、根据题意,可得,即,故此选项不成立,不符合题意;
B、根据题意,可得,故此选项成立,符合题意;
C、根据题意,可得,故此选项不成立,不符合题意;
D、根据题意,可得,故此选项不成立,不符合题意.
故选:B.
5.D
【分析】本题考查了二元一次方程组的解,关键是要理解方程组有无数组解的含义.由关于x,y的方程组有无数组解,求出关于a,b的等式,再根据题意判断即可.
【详解】解∶
,得,
∵方程组有无数组解,
∴,,
∴,,
故选∶D.
6.A
【分析】本题考查几何命题的真假判断,需逐一分析各选项是否符合相关定理或定义,熟练掌握同位角的定义、直角的定义、对顶角的定义以及补角的定义是解此题的关键.
【详解】解:A、同位角相等:只有当两直线平行时,同位角才相等;若两直线不平行,同位角不一定相等;因此该命题缺少前提条件,是假命题,符合题意;
B、直角都相等:直角均为,度数固定,故所有直角都相等,为真命题,故不符合题意;
C、对顶角相等:根据对顶角定理,对顶角一定相等,为真命题,故不符合题意;
D、同角的补角相等:同一个角的补角均为减去该角,度数相同,故相等,为真命题,故不符合题意;
故选:A.
7.C
【分析】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.需要注意的是:如果是表示大于或小于号的点要用空心圆圈,如果是表示大于等于或小于等于号的点要用实心圆点.分别求解两个不等式,得到不等式组的解集,然后判断即可.
【详解】解:
解不等式①得:,
∴不等式组的解集为:,
∴表示在数轴上为:
故选:C.
8.C
【分析】本题考查了换元代入法求代数式的值.通过变量替换简化方程,利用完全平方公式求出,再利用平方差公式求解.
【详解】解:设,则
代入原方程得:,
整理得:,
所求表达式为:,
故选:C.
9.D
【分析】本题主要考查二元一次方程组的运用,理解数量关系是关键,根据题意,每人分7两缺7两,每人分5两多5两,建立方程组即可.
【详解】解:设共有人,两银子,
∵总需银两为,实际银两比所需少7两,
∴,
∵总需银两为,实际银两比所需多5两,
∴,
联立方程得:,
故选:D.
10.C
【分析】本题考查了平移的性质,根据平移的性质逐项分析即可得解,熟练掌握平移的性质是解此题的关键.
【详解】解:由平移的性质可得:,,,,,故①②③④正确,
∴,
∴,即,故⑥正确;
由已知条件不能说明,故⑤错误;
综上所述,正确的有个,
故选:C.
11.两个三角形面积相等则这两个三角形全等
【分析】本题考查了命题的逆命题,掌握逆命题的书写方法是关键.
对于两个命题,如果一个命题的条件和结论分别是另外一个命题的结论和条件,那么这两个命题叫做互逆命题,确定条件和结论,根据逆命题的书写方法即可求解.
【详解】解:“两个全等三角形的面积相等”的条件是“两个三角形全等”,结论是“这两个三角形的面积相等”,
∴逆命题为:两个三角形面积相等则这两个三角形全等,
故答案为:两个三角形面积相等则这两个三角形全等 .
12.(答案不唯一)
【分析】本题考查了二次一次方程组的定义和二元一次方程组的解,能熟记二元一次方程组的定义是解此题的关键.
此题是一道开放型的题目,答案不唯一,只要根据二次一次方程组的定义和二元一次方程组的解写出一个方程组即可.
【详解】解:解为的二元一次方程有.
故答案为:(答案不唯一).
13.
【分析】本题考查了同底数幂乘法的逆运算,利用同底数幂乘法的逆运算计算即可,掌握同底数幂乘法的逆运算是解题的关键.
【详解】解:∵,,
∴,
故答案为:.
14.
【分析】本题主要考查解一元一次不等式组和一元一次方程的整数值,解不等式组,结合其解集得出,解方程得出其解,结合解均为非负整数得出,综合前面的取值范围确定的最终取值,从而得出答案.
【详解】解:,
解不等式①得,
解不等式②得,
∵不等式的解集为,
,即,
解方程得,
∵方程有非负整数解,
,即,
应为偶数,即应为奇数,
符合条件的整数为,,,,
即符合条件的整数的和是.
故答案为:.
15.6
【分析】此题主要考查了一元一次不等式的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.设购买x套新设备第一种办法比第二种办法得到的更优惠,构建不等式求解即可.
【详解】解:设购买x套新设备第一种办法比第二种办法得到的更优惠.由题意得:
,
解得:.
故至少需要购买6套新设备.
故答案为:6.
16.80
【分析】本题考查旋转的性质,由旋转得,再根据可得答案.
【详解】解:由旋转得,,
∵,
∴.
故答案为:80.
17.8
【分析】本题主要考查了一元一次不等式组的整数解及一元一次方程的解,先根据所给方程的解为非负整数,得出a的取值范围,再结合所给不等式组的整数解只有3个即可解决问题.
【详解】解:由方程得,,
因为关于x的方程的解是非负整数,
所以,
解得,
解不等式组得,,
因为此不等式组有且仅有3个整数解,
所以,
解得,
∵为整数,
∴或5,
所以符合条件的所有整数a的和是:.
故答案为:8.
18.
【分析】本题考查解二元一次方程组,根据代入消元法解方程组即可求解.
【详解】解:,
由①得,③
把③代入②,得,
解这个方程,得,
把代入③,得,
所以这个方程组的解是.
19.,将解集表示在数轴上见解析
【分析】本题考查了解一元一次不等式组.也考查了在数轴上表示不等式的解集.分别解两个不等式,再根据大于小的小于大的取中间确定不等式组的解集,然后用数轴表示解集.
【详解】解:解不等式得,
解不等式得,
则不等式组的解集为,
解集在数轴上表示如解图所示.
.
20.(1)
(2)
【分析】本题考查了整式的运算,熟练掌握单项式乘以多项式,幂的运算是解题的关键;
(1)利用单项式乘以多项式的运算法则求解即可;
(2)根据零指数幂,有理数的乘方以及负整数指数幂进行计算即可求解.
【详解】(1)解:
(2)
21.(1)制作一个传统人物皮影需牛皮2平方分米,制作一个动物皮影需牛皮3平方分米
(2)10个
【分析】本题考查二元一次方程组、一元一次不等式解应用题,读懂题意,准确列出方程组及不等式求解是解决问题的关键.
(1)设制作一个传统人物皮影需平方分米的牛皮,制作一个动物皮影需平方分米的牛皮,读懂题意,找准等量关系列二元一次方程组求解即可得到答案;
(2)设制作传统人物皮影个,则制作动物皮影个,读懂题意,列出一元一次不等式求解即可得到答案.
【详解】(1)解:设制作一个传统人物皮影需平方分米的牛皮,制作一个动物皮影需平方分米的牛皮,
由题意得:,
解得,
答:制作一个传统人物皮影需牛皮2平方分米,制作一个动物皮影需牛皮3平分米;
(2)解:设制作传统人物皮影个,则制作动物皮影个,
由题意得,
解得,
答:最少可制作传统人物皮影10个.
22.(1)
(2)
(3)或2
【分析】本题考查的是方程组与不等式组的综合应用,一元一次方程的整数解问题;
(1)利用加减消元法先求解,再求解即可;
(2)由方程的解为正数可得,再解不等式组即可;
(3)由得,,结合方程的解是整数,且m也是整数,,再进一步解答即可.
【详解】(1)解:
由①②得,
∴,
将代入②得,
∴,
∴;
(2)解:∵
∴,
解得;
(3)解:由得,,
∵方程的解是整数,且m也是整数,
∴,
即,
又因为,
∴或2.
23.(1)见解析
(2)
(3)见解析
【分析】本题主要考查了画平移图形,画旋转图形,平移的性质,熟知相关知识是解题的关键.
(1)根据平移方式找到的位置,描出,并顺次连接即可;
(2)由平移的性质即可得到答案;
(3)根据旋转方式和网格的特点找到的位置,描出,并顺次连接即可.
【详解】(1)解:如图所示,即为所求;
(2)解:由平移的性质可得.
(3)解:如图所示,即为所求.
24.;();().
【分析】本题考查了平方差公式的几何图形,完全平方公式,表示图中阴影部分面积是解题的关键.
根据题意分别求出图与图阴影部分面积,然后由面积相等即可求解;
()利用平方差公式即可求解;
()利用平方差公式和完全平方公式即可求解.
【详解】解:图阴影面积:,图阴影面积:,
∵图与图阴影部分面积相等,
∴,
故答案为:;
()
;
()
.
25.(1)绢布扇的单价是15元,手账本的单价是20元
(2)购买6个绢布扇,1个手账本时,获得的投壶机会最多
【分析】本题主要考查了二元一次方程组的实际应用,根据题意,正确列方程或方程组是解题的关键;
(1)设绢布扇的单价是x元,手账本的单价是y元,根据题意列出方程组求解即可;
(2)设购买m个绢布扇,n个手账本,根据题意列出方程,求出m、n的值,再求出的最大值即可得到结论.
【详解】(1)设绢布扇的单价是x元,手账本的单价是y元.
根据题意,得,
解得,
答:绢布扇的单价是15元,手账本的单价是20元;
(2)设购买m个绢布扇,n个手账本.
根据题意,得.
,
又m,n均为正整数,
或,
或,,
购买一件文创商品可获得一次投壶机会,
购买6个绢布扇,1个手账本时,获得的投壶机会最多.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
