苏教版高中数学必修第一册第1章集合1.1集合的概念与表示教学课件(共97张PPT)
文档属性
| 名称 | 苏教版高中数学必修第一册第1章集合1.1集合的概念与表示教学课件(共97张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览









文档简介
(共97张PPT)
苏教版2019高一数学(必修一)第一章 集合
1.1 集合的概念与表示
学习目标
1.通过实例了解集合的含义;理解元素与集合的属于关系.
2.记住常用数集的表示符号,并会应用.
3.通过集合概念及元素与集合关系的学习,培养数学抽象素养,
提升数学运算素养.
军训的时候,随着教官一声口令“高一(1)班集合”,高一(1)班的同学都从四面八方聚集到教官的身边来,不是高一(1)班的同学就会自动走开,这样就把“一些确定的不同的对象”聚集在一起了.这就是我们将要学习的集合问题.
情景导入
在初中的数学学习中,我们曾做过下面的作业:
这里有“正数集合”“负数集合”“整数集合”“分数集合”,那么,什么是集合 如何用数学语言表示集合
新知探究
集合与元素
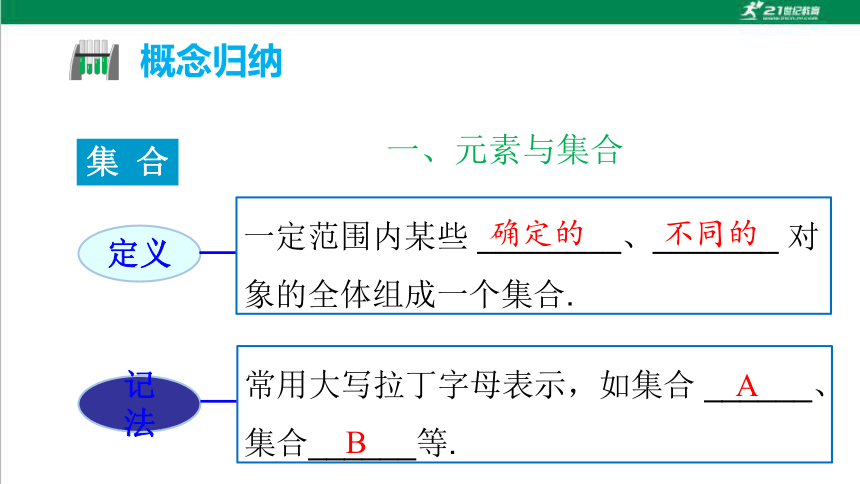
一、元素与集合
集 合
定义
记 法
一定范围内某些 ________、_______ 对象的全体组成一个集合.
确定的
不同的
常用大写拉丁字母表示,如集合 ______、集合______等.
A
B
概念归纳
元 素
定义
记 法
集合中的 __________ 称为该集合的元素,简称元.
每一个对象
常用小写的拉丁字母a,b,c,···表示.
概念归纳
“中国的直辖市”组成一个集合,该集合的元素就是北京、天津上海和重庆这 4 个城市.
“young 中的字母”组成一个集合,该集合的元素就是 y,o,u,n,g 这5个字母.
“book 中的字母”也组成一个集合,该集合的元素就是 b,o,k 这3个字母.
“1~10 以内的所有质数”组成一个集合,该集合的元素就是 2,3,5,7这4个数.
(1)某班所有的“帅哥”能否构成一个集合
(2)某班身高高于175厘米的男生能否构成一个集合
提示 (1)某班所有的“帅哥”不能构成集合,因为“帅哥”没有明确的标准.
(2)某班身高高于175厘米的男生能构成一个集合,因为标准确定.
议一议
【思考】
(1) 集合中的“研究对象”所指的就是数学中的数、点、 代数式吗
提示:集合中的“研究对象”所指的范围非常广泛,可以是数学中的数、点、代数式,也可以是现实生活中的各种各样的事物或人等.
(2) 根据集合的定义思考:集合中的元素具有哪些特性
提示:确定性、互异性和无序性.
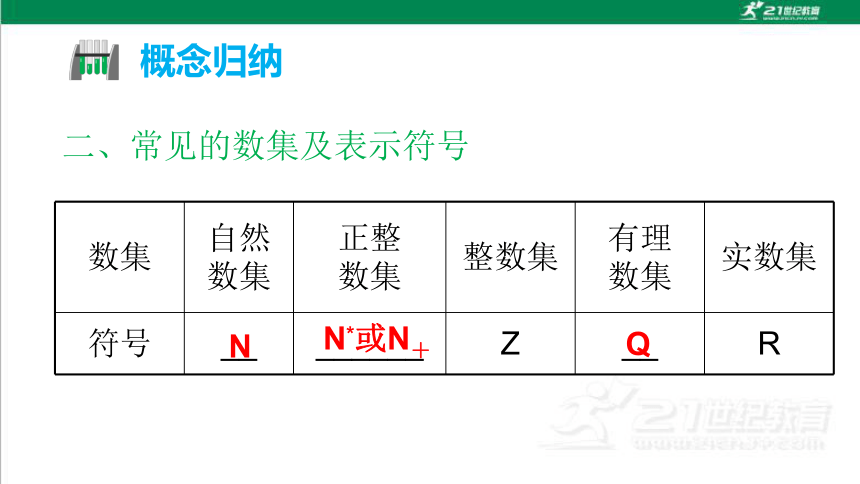
二、常见的数集及表示符号
数集 自然数集 正整
数集 整数集 有理
数集 实数集
符号 __ ______ Z __ R
N
N*或N+
Q
概念归纳
特别地,全体自然数组成的集合,叫作自然数集,记作 N;
全体正整数组成的集合,叫作正整数集,记作 N*或N+;
全体整数组成的集合,叫作整数集,记作 Z;
全体有理数组成的集合,叫作有理数集,记作 Q;
全体实数组成的集合,叫作实数集,记作 R.
概念归纳
【思考】
N 与 N+ (或N*) 有何区别
提示:N+ (或N*) 是所有正整数组成的集合,而N是由0和所有的正整数组成的集合,所以N比N+ (或N*) 多一个元素0.
三.元素与集合的关系
知识点 关系 概念 记法 读法
元素与
集合的关系 属于 如果a是集合A中的元素,就说a______A ________ “a属于A”
不属于 如果a不是集合A中的元素,就说a________A ________ “a不属于A”
属于
a∈A
不属于
a A
概念归纳
【思考】
元素与集合之间有第三种关系吗
提示:对于一个元素a与一个集合A而言,只有
“a∈A”与“a A”这两种结果.
例1.考察下列每组对象,能构成集合的是( )
①中国各地最美的乡村;
②直角坐标系中横、纵坐标相等的点;
③不小于3的自然数;
④第31届奥运会金牌获得者.
A.③④ B.②③④
C.②③ D.②④
答案 B
解析 ①中“最美”标准不明确,不符合确定性,②③④中的元素标准明确,均可构成集合,故选B.
典例剖析
B
1.判断下列说法是否正确,并说明理由.
(1)大于3小于5的所有自然数构成一个集合;
(2)平面直角坐标系中第一象限的一些点组成一个集合;
(3)方程(x-1)2(x+2)=0所有解组成的集合有3个元素.
解 (1)正确,(1)中的元素是确定的,可以构成一个集合.
(2)不正确,“一些点”标准不明确,不能构成一个集合.
(3)不正确,方程的解只有1和-2,集合中有2个元素.
练一练
点拨:判断一组对象能否组成集合的标准
判断一组对象能否组成集合,关键看该组对象是否满足确定性,如果此组对象满足确定性,就可以组成集合;否则,不能组成集合.同时还要注意集合中元素的互异性、无序性.
例2.(1)下列所给关系正确的个数是( )
①π∈R;② Q;③-1∈N*;④|-5| N*.
A.1 B.2 C.3 D.4
(2)已知集合A含有三个元素2,4,6,且当a∈A时,有6-a∈A,那么a为( )
A.2 B.2或4
C.4 D.6
B
B
典例剖析
解析 (1)①π是实数,所以π∈R正确;
③-1不是正整数,所以-1∈N*错误;
④|-5|=5为正整数,所以|-5| N*错误.故选B.
(2)a=2∈A,6-a=4∈A,所以a=2符合题意;a=4∈A,6-a=2∈A,所以a=4符合题意;a=6∈A,6-a=0 A,所以a=6不符合题意.综上所述,a=2或4.故选B.
点拨:判断元素与集合间关系的方法
判断一个对象是否为某个集合的元素,就是判断这个对象是否具有这个集合的元素的共同特征.如果一个对象是某个集合的元素,那么这个对象必定具有这个集合的元素的共同特征.
练一练
例3.已知集合A含有两个元素1和a2,若a∈A,求实数a的值.
解 由题意可知,a=1或a2=a,
(1)若a=1,则a2=1,这与a2≠1相矛盾,故a≠1.
(2)若a2=a,则a=0或a=1(舍去),又当a=0时,A中含有元素1和0,满足集合中元素的互异性,符合题意.
综上可知,实数a的值为0.
典例剖析
延伸探究:若本例去掉条件“a∈A”,其他条件不变,求实数a组成的集合.
解 由集合中元素的互异性可知a2≠1,即a≠±1.故实数a组成的集合为{a|a≠±1,a∈R}.
点拨:解含参元素与集合之间关系问题的求解策略
(1)常用到分类讨论的思想,在进行分类讨论时,务必明确分类标准.
(2)本例题在解方程求得a的值后,常因忘记验证集合中元素的互异性,而造成过程性失分.
例4.已知集合A是由方程ax2-3x-4=0(a∈R)的实数根组成的.
(1)当A中有且只有一个元素时,求a的值,并求此元素;
(2)当A中有两个元素时,求a满足的条件;
(3)当A中至少有一个元素时,求a满足的条件.
典例剖析
解 (1)当A中有且只有一个元素时,要分方程ax2-3x-4=0是一元一次方程还是一元二次方程来解决,若方程是一元一次方程,则有且只有一个根;若方程是一元二次方程,则有两个相等的实数根.
(2)集合A中有两个元素,即方程ax2-3x-4=0有两个不相等的实数根.
分类讨论思想在集合中的应用
求解集合中参数的值常与方程知识相联系,结合集合中元素的特性(确定性、无序性、互异性),通过解方程(组),求出集合中参数的值.
对于“方程ax2+bx+c=0”要分两种情况加以讨论:①当a=0,b≠0时,该方程是一元一次方程.②当a≠0时,该方程是一元二次方程,也只有在这种情况下才能用判别式Δ来确定方程实数根的情况.
点拨:
判断形如ax2+bx+c=0的方程实数根的个数的方法:
(1)当a=0时,原方程可化为bx+c=0的形式,再根据b的取值
讨论方程根的个数:
②若b=0,c=0,则任意一个实数均为方程的实数根;
③若b=0,c≠0,则方程无实数根.
(2)当a≠0时,需根据Δ的值与0的大小关系来确定方程根的个数:
①若Δ=b2-4ac>0,则方程有两个不相等的实数根;
②若Δ=b2-4ac=0,则方程有两个相等的实数根;
③若Δ=b2-4ac<0,则方程无实数根.
1.由“look”中的字母组成的集合中元素个数为( )
A.1 B.2 C.3 D.4
答案 C
解析 集合中任何两个元素都不相同,所以集合中的元素有3个,分别是l,o,k.故选C.
练一练
2.思考辨析,判断正误
(1)漂亮的花可以组成集合.( )
提示 “漂亮的花”具有不确定性,故不能组成集合.
(2)元素1,2,3和元素3,2,1组成的集合不是同一集合.( )
提示 集合中的元素具有无序性,所以元素1,2,3和元素3,2,1组成的集合是同一集合.
(3)若直线y=x+1上的所有点构成集合A,则点(1,2)∈A.( )
(4)若a∈Q,则一定有a∈R.( )
×
×
√
√
练一练
3.已知集合A含有三个元素1,a,a-1,若-2∈A,则实数a的值为( )
A.-2 B.-1
C.-1或-2 D.-2或-3
解析 因为集合A含有三个元素1,a,a-1,且-2∈A,所以a=-2或a-1=-2.当a=-2时,A中元素为1,-2,-3,符合题意;当a-1=-2时,a=-1,A中元素为1,-1,-2,也符合题意.故实数a的值为-1或-2.故选C.
练一练
C
B
4.考察下列每组对象,能构成集合的是( )
①中国各地的美丽乡村;
②直角坐标系中横、纵坐标相等的点;
③不小于3的自然数;
④截止到2020年1月1日,参加“一带一路”的国家.
A.③④ B.②③④
C.②③ D.②④
解析 ①中“美丽”标准不明确,不符合确定性,②③④中的元素标准明确,均可构成集合,故选B.
练一练
5.已知1,x,x2三个实数构成一个集合,则x满足的条件是( )
A.x≠0 B.x≠1
C.x≠±1 D.x≠0且x≠±1
解析 根据集合中元素的互异性,
D
练一练
6.用“∈”或“ ”填空.
7.已知集合M中有两个元素3和a+1,且4∈M,则实数a= .
答案 3
解析 由题意可知a+1=4,即a=3.
练一练
3
8.集合A中含有三个元素0,1,x,且x2∈A,则实数x的值为 .
答案 -1
解析 当x=0,1,-1时,都有x2∈A,但考虑到集合中元素的互异性,x≠0,x≠1,故x=-1.
-1
练一练
1. 列举法
(1) 方法:将集合的元素_________出来,并置于花括
号_________内.
例如{北京,天津,上海,重庆},{y,o,u,n,g}.
(2) 注意事项:①元素之间要用_______分隔;
②列举时与元素的_______无关.
四、集合的表示
一一列举
“{ }”
逗号
次序
概念归纳
【思考】
一一列举元素时,需要考虑元素的顺序吗
提示:用列举法表示集合时不必考虑元素的顺序.
例如:{a,b}与 {b,a} 表示同一个集合.
2. 描述法
(1) 形式:{ x∣p(x)},其中x为集合的代表元素,p(x)
指元素 x 具有的性质.
(2) 本质:它是集合符号语言的具体体现,可将集
合中元素的规律与性质清楚地表示出来.
如:{ x∣x 为中国的直辖市,{ x∣x 为 young 中的字母},
{ x∣ x<-3,x ∈ R}.
【思考】
{ (x,y) ∣y=x2+2}能否写为{ x∣y=x2+2} 或{ y∣y=x2+2}呢
提示:不能,(x,y) 表示集合的元素是有序实数对或点,而x或y则表示集合的元素是数,所以用描述法表示集合时一定要弄清集合的元素是什么.
3. Venn图法
(1) 形式:画一条封闭的曲线,用它的内部来表示一个集合.
(2) 作用:直观地表示集合.
北京,上海,天津,重庆
(1)
y,o,u,n,g
(2)
例如
例如,由方程 x2-1=0 所有的实数解组成的集合,可以表示为下列形式.
(1) 列举法:{-1,1}(也可以是{1,-1});
一个集合可以用不同的方法表示.
(2) 描述法:{ x∣x2-1=0, x∈R} (也可以是
{ x∣x为方程 x2-1=0 的实数解}).
4. 集合相等
(1) 定义:如果两个集合所含的元素完全相同,那么
称这两个集合相等.
(2) 本质:A与B相等,即A中的元素都是B的元素,
B中的元素也都是A的元素.
例如,{北京,天津,上海,重庆}
={上海,北京,天津,重庆}.
例1.用列举法表示下列集合:
(1) 大于1且小于 13 的所有偶数组成的集合;
解:设大于1且小于 13 的所有偶数组成的集合为 A,
那么A= {2,4,6,8,10,12}.
(2) 由1~15 以内的所有质数组成的集合.
7
解:设由 1~15 以内的所有质数组成的集合为 B,
那么 B = {2,3,5,7,11,13}.
例2.用描述法表示下列集合:
(1) 大于1的所有偶数组成的集合;
解: 设大于1的偶数为 x,并且满足条件
x>1,x=2k,k∈N,
因此,这个集合表示为
A={ x∣x>1,x=2k,k∈N}.
(2) 不等式 2x-3>5 的解集.
解:由 2x-3>5可得x>4,故不等式2x-3>5的解集
为 { x∣x>4,x∈R }.
例1中的集合的元素都有有限个,例2中的集合的元素都有无限个.
五、集合的分类
(1) 含有__________元素的集合称为有限集;
(2) 含有__________元素的集合称为无限集;
(3) _______________的集合称为空集,记作 .
有限个
无限个
不含任何元素
解
典例剖析
解析
B
练一练
解析
C
练一练
解析
B
练一练
解析
有限集
无限集
无限集
有限集
练一练
解
练一练
解析
-1
练一练
1. 用“∈”或“ ”填空:
∈
∈
∈
∈
∈
∈
课本练习
2. 用列举法表示下列集合 :
(1) { x∣ x + 1 = 0};
解: x+1=0
x =-1.
∴{ x ∣ x+1= 0} ={- 1}
综上所述,结论是:{- 1};
课本练习
(2) { x∣ x 为15的正约数 };
解:15=1×15=3×5.
∴{ x∣x 为15的正约数} ={1,3,5,15}
综上所述,结论是:{1,3,5,15};
课本练习
(3) { x∣ x为不大于10 的正偶数}.
解:不大于10 的正偶数是:2,4,6,8,10
∴ { x∣x 为不大于10的正偶数}
={2,4,6,8,10}
综上所述,结论是:{2,4,6,8,10}.
课本练习
3. 用描述法表示下列集合:
(1) 数的集合;
(2) 正数的集合;
解:奇数的集合= {n=2k-1∣k∈Z};
解:正偶数的集合={z=2k∣ k∈N*};
(3) 不等式 x2+1≤0 的解集.
解: x ∈ R,x2≥0,
∴ x2+1≥1,
∴ 不等式 x2+1 < 0的解集为
= { x ∣ x2+1≤0}.
课本练习
4. 用适当的方法表示下列集合:
(1) 方程 x2+2x-15=0 的根的集合;
解:因为方程 x2+2x-15=0的根为 x=-5 或 x=3,
所以方程 x2+2x-15=0 的根的集合为:
{-5,3}.
课本练习
(2) 不等式 4x-3<5的解集.
解:不等式 4x-3<5 的解集为{ x∣x<2}.
课本练习
5. 用列举法表示下列集合:
(1) { a∣0 ≤ a < 6,a∈N };
解:∵0≤a<6 且 a∈N,
∴a = 0,1,2,3,4,5.
∴用列举法表示为{0,1,2,3,4,5}
课本练习
(2) “mathematics 中的字母”组成的集合;
(3) 汉字“永”的笔画组成的集合.
解:∵ mathematics中出现的字母有 a,c,e,h,i,
m,s,t,重复出现的字母只记一次,
∴ 用列举法表示为{a,c,e,h,i,m,s,t};
解:永字的笔画为“、, ,フ, 丿, ”,
∴用列举法表示为{、, ,フ, 丿, ”}.
课本练习
习题1.1
感受 理解
∈
∈
∈
2.用列举法表示下列集合:
(1)(x | x + 3x-18 = 0,x∈R};
(2){x | x为不超过5的自然数};
(3){x|-3<2x-1≤3,x∈Z);
(4){(x,y)|0≤a≤2,0≤y<2,x,y∈Z).
解:(1){3,-6}.
(2){0,1,2,3,4,5}
(3){0,1,2}.
(4){(0,0),(0,1),(1,0),(1,1),(2,0), (2,1).}
感受 理解
感受·理解
3.用描述法表示下列集合:
(1)不等式 3x +2>5 的解集;
(2)平面直角坐标系中第二象限的点组成的集合;
(3)二次函数y=x2-2x+3 图象上的点组成的集合.
解:
(1)由 3x+2>5,得 x>1,故不等式 3x+2>5 的解集为{x|x>1,x∈R} .
(2){(x,y)|x<0,y>0}.
(3){(x,y)|y=x -2x+3}.
4.用“∈”或“ ”填空:
(1)若A={x|x -x=0},则1 A,-1 A;
(2)若B={x|1≤x≤5,x∈N},则1 B,1.5 B;
(3)若C={x|-1∈
∈
5.设a,b 为实数,已知 M ={1,2},N ={a,b},且 M = N,
求 a,b的值.
a=1,b=2 或a=2,b=1.
思考·运用
6.已知 A={x|x=3k+1,k∈Z),问:-1,5,三个数中,哪些数是 A的元素?
思考·运用
7.(写作题)我们使用符号“∈”代表短语“是……的元素”(is an element of).符号“3∈A”表示“3是集合A的元素”.如果“3不是集合A的元素”,那么写成“3 A”.虽然“∈”看起来有点像字母“e”,但这两个符号并不相同,不应混淆.
请查阅有关资料,寻找最先引入符号“∈”的数学家,以及符号“∈”的原始意义等信息,写一篇关于符号“∈”的短文.
探究·拓展
解:“∈”表示一个元素属于某一集合的记号,是意大利数学学家皮亚诺(Peano)在1889年的数学著作中首先使用的.
在数系理论研究方面,皮亚诺作出了重大贡献,在1889年出版的《算术原理新办法》一书中,皮亚诺提出“皮亚诺自然数公理”举世闻名,在书中他还对许多逻辑符号进行了创新在1891年创建了《数学杂志》,皮亚诺在这个杂志上利用数理逻辑符号写下自然数公理,并对它们的独立性进行了证明.皮亚诺于1893年发表《无穷小分析教程》,该书被德国的数学百科全书列在“自L.欧拉(Euler)和A.L,柯西(GAUCHY)时代以来最重要的19本微积分教科书”之中.皮亚诺撰写的《数学百科全书》中有很多地方引人注目,例如推广微分中值定理;多变量函数一致连续性的判定定理;隐函数存在定理以及其可微性定理的证明;部分可微但整体不可微的函数的例子;当时流行的极小理论的反例等.
探究·拓展
易错点1 忽略集合中元素的互异性而致错
解析
{2,4}
错因分析
易错点2 不能正确理解集合的表示方法而致错
解析
A
错因分析
解析
①②③
易错点2 不能正确理解集合的表示方法而致错
错因分析
易错点3 不理解自定义的集合(运算)而致错
解析
D
错因分析
易错点4 不理解集合中元素的确定性而致错
解析
CD
错因分析
解析
B
易错点4 不理解集合中元素的确定性而致错
错因分析
解析
29 970
易错点4 不理解集合中元素的确定性而致错
错因分析
B
一、选择题
1.以下各组对象不能组成集合的是( )
A.中国古代四大发明
B.地球上的小河流
C.方程x2-7=0的实数解
D.周长为10 cm的三角形
解析 因为没有明确的标准确定什么样的河流称为小河流,故地球上的小河流不能组成集合.
分层练习-基础
2.若a是R中的元素,但不是Q中的元素,则a可以是( )
D
分层练习-基础
3.(多选题)下列说法正确的是( )
A.N中最小的元素是1
B.由单词“banana”中的所有字母组成的集合中有3个元素
C.若x∈N,则满足2x-5<0的元素组成的集合中的所有元素之和为3
D.在直角坐标系中,在坐标轴上的所有点组成一个集合
解析 N表示自然数集,最小的元素是0,故A错;B正确,元素分别为字母b,a,n;C中,由2x-5<0且x∈N,知x=0,1,2,故所有元素之和为3,正确;D正确.
BCD
分层练习-基础
4.若a,b,c,d为集合A的四个元素,则以a,b,c,d为边长构成的四边形可能是( )
A.矩形 B.平行四边形
C.菱形 D.梯形
D
解析 由集合中的元素具有互异性可知a,b,c,d互不相等,而梯形的四条边可以互不相等,故选D.
分层练习-基础
5.由a2,2-a,4组成一个集合A,且集合A中含有3个元素,则实数a的取值可以是( )
A.1 B.-2 C.-1 D.2
解析 由题意知a2≠4,2-a≠4,a2≠2-a,解得a≠±2,且a≠1,结合选项知C正确,故选C.
C
分层练习-基础
二、填空题
6.已知集合M中有2个元素x,2-x,若-1 M,则3________M,1________M.(用∈, 填空)
解析 若3∈M,则-1∈M,不合题意,故3 M.当x=1时,2-x=1,M中的两元素为1,1,不合题意,故1 M.
分层练习-基础
7.已知集合A是由0,m,m2-3m+2三个元素构成的集合,且2∈A,则实数m=________.
3
解析 由题意知,m=2或m2-3m+2=2,
解得m=2或m=0或m=3.经验证,
当m=0或m=2时,不满足集合中元素的互异性,
当m=3时,满足题意,故m=3.
分层练习-基础
8.用∈, 填空:
(1)0________N*;
(2)π________Q;
∈
∈
分层练习-基础
三、解答题
9.已知集合A中的元素为0,2,4,2-a,若a2-a+2∈A,求实数a.
解 (1)若a2-a+2=0,无解;
(2)若a2-a+2=2,即a2-a=0,∴a=0或1.
但a=0时,2-a=2,不满足元素互异性,舍去,a=1满足;
(3)若a2-a+2=4,即a2-a-2=0,a=2或a=-1.
但a=2时,2-a=0,不满足元素互异性,舍去,a=-1满足;
(4)若a2-a+2=2-a,a=0,由以上可知不满足题意.
综上,a=1或-1.
分层练习-巩固
10.已知集合A中的元素x满足ax2-3x+1=0,a∈R.
(1)若1∈A,求实数a的值;
(2)若A为单元素集合,求实数a的值;
解 (1)∵1∈A,∴a·12-3×1+1=0,∴a=2.
当a≠0时,要使A为单元素集合,则方程ax2-3x+1=0有两个相等的实数根,
分层练习-巩固
(3)若A为双元素集合,求实数a的取值范围.
解 若A为双元素集合,则方程ax2-3x+1=0有两个不相等的实数根,
∴a≠0且Δ=(-3)2-4a>0,
分层练习-巩固
2
分层练习-巩固
0
3
且3个元素的和为2+(-2)+0=0.
分层练习-巩固
即a2+a-1=0,
(1)若2∈A,任意写出A中的两个元素;
(2)若A为单元素集合,求实数a.
分层练习-巩固
14.对于任意两个自然数m,n,定义 运算如下:当m,n都为奇数或偶数时,m n=m+n;当m,n中一个为偶数,另一个为奇数时,m n=mn,则在此定义下,集合M中满足a b=18,a∈N,b∈N的元素(a,b)个数为________.
23
解析 a b=18,a∈N,b∈N,若a和b一奇一偶,则ab=18,满足此条件的有1×18=2×9=3×6,故(a,b)有6个;若a和b都为奇数或偶数,则a+b=18,满足此条件的有1+17=2+16=3+15=4+14=……=17+1,故(a,b)有17个,所以集合M中满足a b=18,a∈N,b∈N的元素(a,b)个数为6+17=23.
分层练习-拓展
1.记牢3个知识点
(1)元素与集合的概念,元素与集合的关系.
(2)常用数集的表示.
(3)集合中元素的特性及应用.
2.掌握2种方法
(1)元素与集合关系的判定方法.
(2)解答含有字母的元素与集合关系的问题时,要有分类讨论意识.
3.注意4个易错点
集合中的元素具有三个特性,求解与集合有关的字母参数值(范围)时,需借助元素的互异性来检验所求参数是否符合要求.
课堂小结
苏教版2019高一数学(必修一)第一章 集合
1.1 集合的概念与表示
学习目标
1.通过实例了解集合的含义;理解元素与集合的属于关系.
2.记住常用数集的表示符号,并会应用.
3.通过集合概念及元素与集合关系的学习,培养数学抽象素养,
提升数学运算素养.
军训的时候,随着教官一声口令“高一(1)班集合”,高一(1)班的同学都从四面八方聚集到教官的身边来,不是高一(1)班的同学就会自动走开,这样就把“一些确定的不同的对象”聚集在一起了.这就是我们将要学习的集合问题.
情景导入
在初中的数学学习中,我们曾做过下面的作业:
这里有“正数集合”“负数集合”“整数集合”“分数集合”,那么,什么是集合 如何用数学语言表示集合
新知探究
集合与元素
一、元素与集合
集 合
定义
记 法
一定范围内某些 ________、_______ 对象的全体组成一个集合.
确定的
不同的
常用大写拉丁字母表示,如集合 ______、集合______等.
A
B
概念归纳
元 素
定义
记 法
集合中的 __________ 称为该集合的元素,简称元.
每一个对象
常用小写的拉丁字母a,b,c,···表示.
概念归纳
“中国的直辖市”组成一个集合,该集合的元素就是北京、天津上海和重庆这 4 个城市.
“young 中的字母”组成一个集合,该集合的元素就是 y,o,u,n,g 这5个字母.
“book 中的字母”也组成一个集合,该集合的元素就是 b,o,k 这3个字母.
“1~10 以内的所有质数”组成一个集合,该集合的元素就是 2,3,5,7这4个数.
(1)某班所有的“帅哥”能否构成一个集合
(2)某班身高高于175厘米的男生能否构成一个集合
提示 (1)某班所有的“帅哥”不能构成集合,因为“帅哥”没有明确的标准.
(2)某班身高高于175厘米的男生能构成一个集合,因为标准确定.
议一议
【思考】
(1) 集合中的“研究对象”所指的就是数学中的数、点、 代数式吗
提示:集合中的“研究对象”所指的范围非常广泛,可以是数学中的数、点、代数式,也可以是现实生活中的各种各样的事物或人等.
(2) 根据集合的定义思考:集合中的元素具有哪些特性
提示:确定性、互异性和无序性.
二、常见的数集及表示符号
数集 自然数集 正整
数集 整数集 有理
数集 实数集
符号 __ ______ Z __ R
N
N*或N+
Q
概念归纳
特别地,全体自然数组成的集合,叫作自然数集,记作 N;
全体正整数组成的集合,叫作正整数集,记作 N*或N+;
全体整数组成的集合,叫作整数集,记作 Z;
全体有理数组成的集合,叫作有理数集,记作 Q;
全体实数组成的集合,叫作实数集,记作 R.
概念归纳
【思考】
N 与 N+ (或N*) 有何区别
提示:N+ (或N*) 是所有正整数组成的集合,而N是由0和所有的正整数组成的集合,所以N比N+ (或N*) 多一个元素0.
三.元素与集合的关系
知识点 关系 概念 记法 读法
元素与
集合的关系 属于 如果a是集合A中的元素,就说a______A ________ “a属于A”
不属于 如果a不是集合A中的元素,就说a________A ________ “a不属于A”
属于
a∈A
不属于
a A
概念归纳
【思考】
元素与集合之间有第三种关系吗
提示:对于一个元素a与一个集合A而言,只有
“a∈A”与“a A”这两种结果.
例1.考察下列每组对象,能构成集合的是( )
①中国各地最美的乡村;
②直角坐标系中横、纵坐标相等的点;
③不小于3的自然数;
④第31届奥运会金牌获得者.
A.③④ B.②③④
C.②③ D.②④
答案 B
解析 ①中“最美”标准不明确,不符合确定性,②③④中的元素标准明确,均可构成集合,故选B.
典例剖析
B
1.判断下列说法是否正确,并说明理由.
(1)大于3小于5的所有自然数构成一个集合;
(2)平面直角坐标系中第一象限的一些点组成一个集合;
(3)方程(x-1)2(x+2)=0所有解组成的集合有3个元素.
解 (1)正确,(1)中的元素是确定的,可以构成一个集合.
(2)不正确,“一些点”标准不明确,不能构成一个集合.
(3)不正确,方程的解只有1和-2,集合中有2个元素.
练一练
点拨:判断一组对象能否组成集合的标准
判断一组对象能否组成集合,关键看该组对象是否满足确定性,如果此组对象满足确定性,就可以组成集合;否则,不能组成集合.同时还要注意集合中元素的互异性、无序性.
例2.(1)下列所给关系正确的个数是( )
①π∈R;② Q;③-1∈N*;④|-5| N*.
A.1 B.2 C.3 D.4
(2)已知集合A含有三个元素2,4,6,且当a∈A时,有6-a∈A,那么a为( )
A.2 B.2或4
C.4 D.6
B
B
典例剖析
解析 (1)①π是实数,所以π∈R正确;
③-1不是正整数,所以-1∈N*错误;
④|-5|=5为正整数,所以|-5| N*错误.故选B.
(2)a=2∈A,6-a=4∈A,所以a=2符合题意;a=4∈A,6-a=2∈A,所以a=4符合题意;a=6∈A,6-a=0 A,所以a=6不符合题意.综上所述,a=2或4.故选B.
点拨:判断元素与集合间关系的方法
判断一个对象是否为某个集合的元素,就是判断这个对象是否具有这个集合的元素的共同特征.如果一个对象是某个集合的元素,那么这个对象必定具有这个集合的元素的共同特征.
练一练
例3.已知集合A含有两个元素1和a2,若a∈A,求实数a的值.
解 由题意可知,a=1或a2=a,
(1)若a=1,则a2=1,这与a2≠1相矛盾,故a≠1.
(2)若a2=a,则a=0或a=1(舍去),又当a=0时,A中含有元素1和0,满足集合中元素的互异性,符合题意.
综上可知,实数a的值为0.
典例剖析
延伸探究:若本例去掉条件“a∈A”,其他条件不变,求实数a组成的集合.
解 由集合中元素的互异性可知a2≠1,即a≠±1.故实数a组成的集合为{a|a≠±1,a∈R}.
点拨:解含参元素与集合之间关系问题的求解策略
(1)常用到分类讨论的思想,在进行分类讨论时,务必明确分类标准.
(2)本例题在解方程求得a的值后,常因忘记验证集合中元素的互异性,而造成过程性失分.
例4.已知集合A是由方程ax2-3x-4=0(a∈R)的实数根组成的.
(1)当A中有且只有一个元素时,求a的值,并求此元素;
(2)当A中有两个元素时,求a满足的条件;
(3)当A中至少有一个元素时,求a满足的条件.
典例剖析
解 (1)当A中有且只有一个元素时,要分方程ax2-3x-4=0是一元一次方程还是一元二次方程来解决,若方程是一元一次方程,则有且只有一个根;若方程是一元二次方程,则有两个相等的实数根.
(2)集合A中有两个元素,即方程ax2-3x-4=0有两个不相等的实数根.
分类讨论思想在集合中的应用
求解集合中参数的值常与方程知识相联系,结合集合中元素的特性(确定性、无序性、互异性),通过解方程(组),求出集合中参数的值.
对于“方程ax2+bx+c=0”要分两种情况加以讨论:①当a=0,b≠0时,该方程是一元一次方程.②当a≠0时,该方程是一元二次方程,也只有在这种情况下才能用判别式Δ来确定方程实数根的情况.
点拨:
判断形如ax2+bx+c=0的方程实数根的个数的方法:
(1)当a=0时,原方程可化为bx+c=0的形式,再根据b的取值
讨论方程根的个数:
②若b=0,c=0,则任意一个实数均为方程的实数根;
③若b=0,c≠0,则方程无实数根.
(2)当a≠0时,需根据Δ的值与0的大小关系来确定方程根的个数:
①若Δ=b2-4ac>0,则方程有两个不相等的实数根;
②若Δ=b2-4ac=0,则方程有两个相等的实数根;
③若Δ=b2-4ac<0,则方程无实数根.
1.由“look”中的字母组成的集合中元素个数为( )
A.1 B.2 C.3 D.4
答案 C
解析 集合中任何两个元素都不相同,所以集合中的元素有3个,分别是l,o,k.故选C.
练一练
2.思考辨析,判断正误
(1)漂亮的花可以组成集合.( )
提示 “漂亮的花”具有不确定性,故不能组成集合.
(2)元素1,2,3和元素3,2,1组成的集合不是同一集合.( )
提示 集合中的元素具有无序性,所以元素1,2,3和元素3,2,1组成的集合是同一集合.
(3)若直线y=x+1上的所有点构成集合A,则点(1,2)∈A.( )
(4)若a∈Q,则一定有a∈R.( )
×
×
√
√
练一练
3.已知集合A含有三个元素1,a,a-1,若-2∈A,则实数a的值为( )
A.-2 B.-1
C.-1或-2 D.-2或-3
解析 因为集合A含有三个元素1,a,a-1,且-2∈A,所以a=-2或a-1=-2.当a=-2时,A中元素为1,-2,-3,符合题意;当a-1=-2时,a=-1,A中元素为1,-1,-2,也符合题意.故实数a的值为-1或-2.故选C.
练一练
C
B
4.考察下列每组对象,能构成集合的是( )
①中国各地的美丽乡村;
②直角坐标系中横、纵坐标相等的点;
③不小于3的自然数;
④截止到2020年1月1日,参加“一带一路”的国家.
A.③④ B.②③④
C.②③ D.②④
解析 ①中“美丽”标准不明确,不符合确定性,②③④中的元素标准明确,均可构成集合,故选B.
练一练
5.已知1,x,x2三个实数构成一个集合,则x满足的条件是( )
A.x≠0 B.x≠1
C.x≠±1 D.x≠0且x≠±1
解析 根据集合中元素的互异性,
D
练一练
6.用“∈”或“ ”填空.
7.已知集合M中有两个元素3和a+1,且4∈M,则实数a= .
答案 3
解析 由题意可知a+1=4,即a=3.
练一练
3
8.集合A中含有三个元素0,1,x,且x2∈A,则实数x的值为 .
答案 -1
解析 当x=0,1,-1时,都有x2∈A,但考虑到集合中元素的互异性,x≠0,x≠1,故x=-1.
-1
练一练
1. 列举法
(1) 方法:将集合的元素_________出来,并置于花括
号_________内.
例如{北京,天津,上海,重庆},{y,o,u,n,g}.
(2) 注意事项:①元素之间要用_______分隔;
②列举时与元素的_______无关.
四、集合的表示
一一列举
“{ }”
逗号
次序
概念归纳
【思考】
一一列举元素时,需要考虑元素的顺序吗
提示:用列举法表示集合时不必考虑元素的顺序.
例如:{a,b}与 {b,a} 表示同一个集合.
2. 描述法
(1) 形式:{ x∣p(x)},其中x为集合的代表元素,p(x)
指元素 x 具有的性质.
(2) 本质:它是集合符号语言的具体体现,可将集
合中元素的规律与性质清楚地表示出来.
如:{ x∣x 为中国的直辖市,{ x∣x 为 young 中的字母},
{ x∣ x<-3,x ∈ R}.
【思考】
{ (x,y) ∣y=x2+2}能否写为{ x∣y=x2+2} 或{ y∣y=x2+2}呢
提示:不能,(x,y) 表示集合的元素是有序实数对或点,而x或y则表示集合的元素是数,所以用描述法表示集合时一定要弄清集合的元素是什么.
3. Venn图法
(1) 形式:画一条封闭的曲线,用它的内部来表示一个集合.
(2) 作用:直观地表示集合.
北京,上海,天津,重庆
(1)
y,o,u,n,g
(2)
例如
例如,由方程 x2-1=0 所有的实数解组成的集合,可以表示为下列形式.
(1) 列举法:{-1,1}(也可以是{1,-1});
一个集合可以用不同的方法表示.
(2) 描述法:{ x∣x2-1=0, x∈R} (也可以是
{ x∣x为方程 x2-1=0 的实数解}).
4. 集合相等
(1) 定义:如果两个集合所含的元素完全相同,那么
称这两个集合相等.
(2) 本质:A与B相等,即A中的元素都是B的元素,
B中的元素也都是A的元素.
例如,{北京,天津,上海,重庆}
={上海,北京,天津,重庆}.
例1.用列举法表示下列集合:
(1) 大于1且小于 13 的所有偶数组成的集合;
解:设大于1且小于 13 的所有偶数组成的集合为 A,
那么A= {2,4,6,8,10,12}.
(2) 由1~15 以内的所有质数组成的集合.
7
解:设由 1~15 以内的所有质数组成的集合为 B,
那么 B = {2,3,5,7,11,13}.
例2.用描述法表示下列集合:
(1) 大于1的所有偶数组成的集合;
解: 设大于1的偶数为 x,并且满足条件
x>1,x=2k,k∈N,
因此,这个集合表示为
A={ x∣x>1,x=2k,k∈N}.
(2) 不等式 2x-3>5 的解集.
解:由 2x-3>5可得x>4,故不等式2x-3>5的解集
为 { x∣x>4,x∈R }.
例1中的集合的元素都有有限个,例2中的集合的元素都有无限个.
五、集合的分类
(1) 含有__________元素的集合称为有限集;
(2) 含有__________元素的集合称为无限集;
(3) _______________的集合称为空集,记作 .
有限个
无限个
不含任何元素
解
典例剖析
解析
B
练一练
解析
C
练一练
解析
B
练一练
解析
有限集
无限集
无限集
有限集
练一练
解
练一练
解析
-1
练一练
1. 用“∈”或“ ”填空:
∈
∈
∈
∈
∈
∈
课本练习
2. 用列举法表示下列集合 :
(1) { x∣ x + 1 = 0};
解: x+1=0
x =-1.
∴{ x ∣ x+1= 0} ={- 1}
综上所述,结论是:{- 1};
课本练习
(2) { x∣ x 为15的正约数 };
解:15=1×15=3×5.
∴{ x∣x 为15的正约数} ={1,3,5,15}
综上所述,结论是:{1,3,5,15};
课本练习
(3) { x∣ x为不大于10 的正偶数}.
解:不大于10 的正偶数是:2,4,6,8,10
∴ { x∣x 为不大于10的正偶数}
={2,4,6,8,10}
综上所述,结论是:{2,4,6,8,10}.
课本练习
3. 用描述法表示下列集合:
(1) 数的集合;
(2) 正数的集合;
解:奇数的集合= {n=2k-1∣k∈Z};
解:正偶数的集合={z=2k∣ k∈N*};
(3) 不等式 x2+1≤0 的解集.
解: x ∈ R,x2≥0,
∴ x2+1≥1,
∴ 不等式 x2+1 < 0的解集为
= { x ∣ x2+1≤0}.
课本练习
4. 用适当的方法表示下列集合:
(1) 方程 x2+2x-15=0 的根的集合;
解:因为方程 x2+2x-15=0的根为 x=-5 或 x=3,
所以方程 x2+2x-15=0 的根的集合为:
{-5,3}.
课本练习
(2) 不等式 4x-3<5的解集.
解:不等式 4x-3<5 的解集为{ x∣x<2}.
课本练习
5. 用列举法表示下列集合:
(1) { a∣0 ≤ a < 6,a∈N };
解:∵0≤a<6 且 a∈N,
∴a = 0,1,2,3,4,5.
∴用列举法表示为{0,1,2,3,4,5}
课本练习
(2) “mathematics 中的字母”组成的集合;
(3) 汉字“永”的笔画组成的集合.
解:∵ mathematics中出现的字母有 a,c,e,h,i,
m,s,t,重复出现的字母只记一次,
∴ 用列举法表示为{a,c,e,h,i,m,s,t};
解:永字的笔画为“、, ,フ, 丿, ”,
∴用列举法表示为{、, ,フ, 丿, ”}.
课本练习
习题1.1
感受 理解
∈
∈
∈
2.用列举法表示下列集合:
(1)(x | x + 3x-18 = 0,x∈R};
(2){x | x为不超过5的自然数};
(3){x|-3<2x-1≤3,x∈Z);
(4){(x,y)|0≤a≤2,0≤y<2,x,y∈Z).
解:(1){3,-6}.
(2){0,1,2,3,4,5}
(3){0,1,2}.
(4){(0,0),(0,1),(1,0),(1,1),(2,0), (2,1).}
感受 理解
感受·理解
3.用描述法表示下列集合:
(1)不等式 3x +2>5 的解集;
(2)平面直角坐标系中第二象限的点组成的集合;
(3)二次函数y=x2-2x+3 图象上的点组成的集合.
解:
(1)由 3x+2>5,得 x>1,故不等式 3x+2>5 的解集为{x|x>1,x∈R} .
(2){(x,y)|x<0,y>0}.
(3){(x,y)|y=x -2x+3}.
4.用“∈”或“ ”填空:
(1)若A={x|x -x=0},则1 A,-1 A;
(2)若B={x|1≤x≤5,x∈N},则1 B,1.5 B;
(3)若C={x|-1
∈
5.设a,b 为实数,已知 M ={1,2},N ={a,b},且 M = N,
求 a,b的值.
a=1,b=2 或a=2,b=1.
思考·运用
6.已知 A={x|x=3k+1,k∈Z),问:-1,5,三个数中,哪些数是 A的元素?
思考·运用
7.(写作题)我们使用符号“∈”代表短语“是……的元素”(is an element of).符号“3∈A”表示“3是集合A的元素”.如果“3不是集合A的元素”,那么写成“3 A”.虽然“∈”看起来有点像字母“e”,但这两个符号并不相同,不应混淆.
请查阅有关资料,寻找最先引入符号“∈”的数学家,以及符号“∈”的原始意义等信息,写一篇关于符号“∈”的短文.
探究·拓展
解:“∈”表示一个元素属于某一集合的记号,是意大利数学学家皮亚诺(Peano)在1889年的数学著作中首先使用的.
在数系理论研究方面,皮亚诺作出了重大贡献,在1889年出版的《算术原理新办法》一书中,皮亚诺提出“皮亚诺自然数公理”举世闻名,在书中他还对许多逻辑符号进行了创新在1891年创建了《数学杂志》,皮亚诺在这个杂志上利用数理逻辑符号写下自然数公理,并对它们的独立性进行了证明.皮亚诺于1893年发表《无穷小分析教程》,该书被德国的数学百科全书列在“自L.欧拉(Euler)和A.L,柯西(GAUCHY)时代以来最重要的19本微积分教科书”之中.皮亚诺撰写的《数学百科全书》中有很多地方引人注目,例如推广微分中值定理;多变量函数一致连续性的判定定理;隐函数存在定理以及其可微性定理的证明;部分可微但整体不可微的函数的例子;当时流行的极小理论的反例等.
探究·拓展
易错点1 忽略集合中元素的互异性而致错
解析
{2,4}
错因分析
易错点2 不能正确理解集合的表示方法而致错
解析
A
错因分析
解析
①②③
易错点2 不能正确理解集合的表示方法而致错
错因分析
易错点3 不理解自定义的集合(运算)而致错
解析
D
错因分析
易错点4 不理解集合中元素的确定性而致错
解析
CD
错因分析
解析
B
易错点4 不理解集合中元素的确定性而致错
错因分析
解析
29 970
易错点4 不理解集合中元素的确定性而致错
错因分析
B
一、选择题
1.以下各组对象不能组成集合的是( )
A.中国古代四大发明
B.地球上的小河流
C.方程x2-7=0的实数解
D.周长为10 cm的三角形
解析 因为没有明确的标准确定什么样的河流称为小河流,故地球上的小河流不能组成集合.
分层练习-基础
2.若a是R中的元素,但不是Q中的元素,则a可以是( )
D
分层练习-基础
3.(多选题)下列说法正确的是( )
A.N中最小的元素是1
B.由单词“banana”中的所有字母组成的集合中有3个元素
C.若x∈N,则满足2x-5<0的元素组成的集合中的所有元素之和为3
D.在直角坐标系中,在坐标轴上的所有点组成一个集合
解析 N表示自然数集,最小的元素是0,故A错;B正确,元素分别为字母b,a,n;C中,由2x-5<0且x∈N,知x=0,1,2,故所有元素之和为3,正确;D正确.
BCD
分层练习-基础
4.若a,b,c,d为集合A的四个元素,则以a,b,c,d为边长构成的四边形可能是( )
A.矩形 B.平行四边形
C.菱形 D.梯形
D
解析 由集合中的元素具有互异性可知a,b,c,d互不相等,而梯形的四条边可以互不相等,故选D.
分层练习-基础
5.由a2,2-a,4组成一个集合A,且集合A中含有3个元素,则实数a的取值可以是( )
A.1 B.-2 C.-1 D.2
解析 由题意知a2≠4,2-a≠4,a2≠2-a,解得a≠±2,且a≠1,结合选项知C正确,故选C.
C
分层练习-基础
二、填空题
6.已知集合M中有2个元素x,2-x,若-1 M,则3________M,1________M.(用∈, 填空)
解析 若3∈M,则-1∈M,不合题意,故3 M.当x=1时,2-x=1,M中的两元素为1,1,不合题意,故1 M.
分层练习-基础
7.已知集合A是由0,m,m2-3m+2三个元素构成的集合,且2∈A,则实数m=________.
3
解析 由题意知,m=2或m2-3m+2=2,
解得m=2或m=0或m=3.经验证,
当m=0或m=2时,不满足集合中元素的互异性,
当m=3时,满足题意,故m=3.
分层练习-基础
8.用∈, 填空:
(1)0________N*;
(2)π________Q;
∈
∈
分层练习-基础
三、解答题
9.已知集合A中的元素为0,2,4,2-a,若a2-a+2∈A,求实数a.
解 (1)若a2-a+2=0,无解;
(2)若a2-a+2=2,即a2-a=0,∴a=0或1.
但a=0时,2-a=2,不满足元素互异性,舍去,a=1满足;
(3)若a2-a+2=4,即a2-a-2=0,a=2或a=-1.
但a=2时,2-a=0,不满足元素互异性,舍去,a=-1满足;
(4)若a2-a+2=2-a,a=0,由以上可知不满足题意.
综上,a=1或-1.
分层练习-巩固
10.已知集合A中的元素x满足ax2-3x+1=0,a∈R.
(1)若1∈A,求实数a的值;
(2)若A为单元素集合,求实数a的值;
解 (1)∵1∈A,∴a·12-3×1+1=0,∴a=2.
当a≠0时,要使A为单元素集合,则方程ax2-3x+1=0有两个相等的实数根,
分层练习-巩固
(3)若A为双元素集合,求实数a的取值范围.
解 若A为双元素集合,则方程ax2-3x+1=0有两个不相等的实数根,
∴a≠0且Δ=(-3)2-4a>0,
分层练习-巩固
2
分层练习-巩固
0
3
且3个元素的和为2+(-2)+0=0.
分层练习-巩固
即a2+a-1=0,
(1)若2∈A,任意写出A中的两个元素;
(2)若A为单元素集合,求实数a.
分层练习-巩固
14.对于任意两个自然数m,n,定义 运算如下:当m,n都为奇数或偶数时,m n=m+n;当m,n中一个为偶数,另一个为奇数时,m n=mn,则在此定义下,集合M中满足a b=18,a∈N,b∈N的元素(a,b)个数为________.
23
解析 a b=18,a∈N,b∈N,若a和b一奇一偶,则ab=18,满足此条件的有1×18=2×9=3×6,故(a,b)有6个;若a和b都为奇数或偶数,则a+b=18,满足此条件的有1+17=2+16=3+15=4+14=……=17+1,故(a,b)有17个,所以集合M中满足a b=18,a∈N,b∈N的元素(a,b)个数为6+17=23.
分层练习-拓展
1.记牢3个知识点
(1)元素与集合的概念,元素与集合的关系.
(2)常用数集的表示.
(3)集合中元素的特性及应用.
2.掌握2种方法
(1)元素与集合关系的判定方法.
(2)解答含有字母的元素与集合关系的问题时,要有分类讨论意识.
3.注意4个易错点
集合中的元素具有三个特性,求解与集合有关的字母参数值(范围)时,需借助元素的互异性来检验所求参数是否符合要求.
课堂小结
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
