苏教版高中数学必修第一册第2章常用逻辑用语2.3.1全程量词命题与存在量词命题教学课件(共53张PPT)
文档属性
| 名称 | 苏教版高中数学必修第一册第2章常用逻辑用语2.3.1全程量词命题与存在量词命题教学课件(共53张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览











文档简介
(共53张PPT)
苏教版2019高一数学(必修一)第一章 集合
2.3.2 全程量词命题与存在量词命题
学习目标
1.理解全称量词与存在量词的意义.
2.会判断命题是全称量词命题还是存在量词命题,
并会判断它的真假.(重点)
3.用全称量词、存在量词梳理、表达学过的相应数学内容,
重点提升数学抽象、逻辑推理素养.(难点)
情景导入
在某个城市中有一位理发师,他的广告词是这样写的:
“本人的理发技艺十分高超,誉满全城.我将为本城所有不给自己刮脸的人刮脸,我也只给这些人刮脸.我对各位表示热诚欢迎!”
来找他刮脸的人络绎不绝,这些人自然都是那些不给自己刮脸的人.
可是,有一天,这位理发师从镜子里看见自己的胡子长了,他本能地抓起了剃刀.
你们觉得他能不能给自己刮脸呢
如果他不给自己刮脸,他就属于“不给自己刮脸的人”,他就要给自己刮脸.而如果他给自己刮脸,他又属于“给自己刮脸的人”,他就不该给自己刮脸.
这就是著名的“罗素理发师悖论”问题,如果我们学习了全称量词命题与存在量词命题的知识,就可以通过逻辑推理方法进行分析了.
在日常生活和学习中,我们经常遇到这样的语句:
(1)对任意实数 x,都有 x >0;
(2)存在有理数x,使x -2=0;
(3)有的矩形是菱形;
(4)所有的质数都是奇数;
(5)有一个素数是偶数.
这些语句中用到了“任意”“存在”“有的”等词,它们表示什么含义?
1.全称量词与存在量词
新知探究
语句(1)使用了“任意”,
表示对每一个实数x,必定有“x ≥0”,
即没有使“x ≥0”不成立的实数x存在.
语句(2)使用了“存在”,
表示至少可以找到一个有理数 x,使“x —2 = 0”成立.
语句(3)使用了“有的”,
表示可以找到一个矩形,它是菱形.
语句(4)使用了“所有”,
表示每一个质数都是奇数.
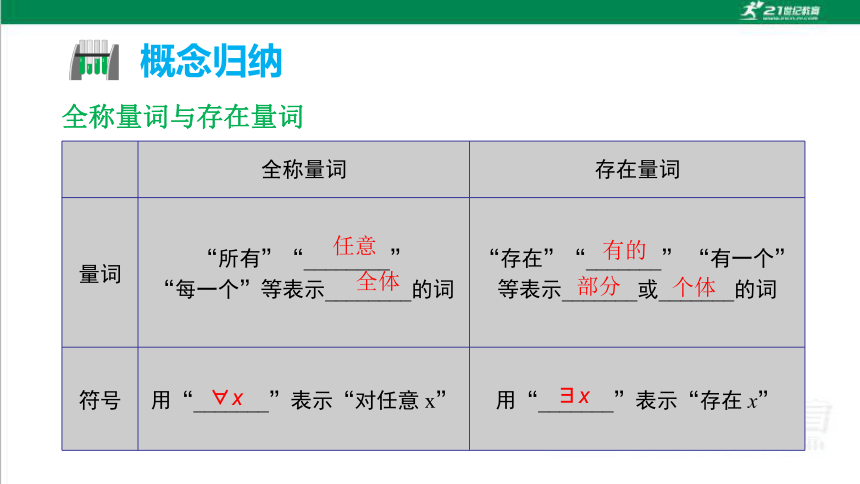
全称量词与存在量词
全称量词 存在量词
量词 “所有”“________”
“每一个”等表示________的词 “存在”“_______” “有一个”等表示_______或_______的词
符号 用“_______”表示“对任意 x” 用“_______”表示“存在 x”
任意
全体
有的
部分
个体
x
x
概念归纳
例如:
上面的语句(1)可以表示为“ ∈R,x ≥ 0”,
即“任意实数的平方都不小于 0”.
上面的语句(2)可以表示为“ x∈Q,x —2=0”,
即“方程x -2 =0 存在有理数解”.
那么你知道常见的全称量词、存在量词还有哪些
答:(答案不唯一)
常见的全称量词还有“一切”“任给”“凡是”等.
常见的存在量词还有“有些”“对某些”“有的”等.
想一想
(1) 定义和表示方法:
全称量词命题 存在量词命题
定义 含有_________的命题称为全称量词命题 含有_________的命题称为存在量词命题
表示 一般形式可表示为:____________ 一般形式可表示为:____________
全称量词
存在量词
x∈M,p(x)
x∈M,p(x)
2.全称量词命题与存在量词命题
新知探究
(2) 本质:
全称量词的含义是“任意性”,存在量词的含义是“存在性”.
(3) 应用:
全称量词、存在量词是数学和日常生活中使用频率很高的一种逻辑用语,数学中存在大量的全称量词命题和存在量词命题.
概念归纳
全称量词命题中的“x,M与p(x)”表达的含义分别是什么
答:元素x可以表示实数、方程、函数、不等式,也可以表示几何图形,
相应的集合M是这些元素的某一特定的范围,
p(x)表示集合M的所有元素满足的性质,也可以用q(x),r(x)等符号表示.
想一想
判断下列命题的真假:
课本例1
解:因为对任意实数x,都有 x2≥0 ,
所以对任意实数x,都有 x2+2≥2>0,
即对任意实数x,都有 x2+2>0 成立,
因此,“ x∈R,x2+2>0”是真命题.
由例1我们发现:
要判定一个存在量词命题为真,只要在给定的集合中找到一个元素,使命题为真即可;否则命题为假.
要判定一个全称量词命题为真,必须对给定的集合中的每一个元素,命题都为真;但要判定一个全称量词命题为假,只要在给定的集合中找到一个元素,使命题为假.
概念归纳
给定的集合对存在量词命题、全称量词命题的真假有没有影响
试举例说明.
思考探究
例 1.判断下列命题是全称量词命题还是存在量词命题,并判断其真假.
(1)平面内,凸多边形的外角和等于360° ;
(2)至少有一个整数,它既能被11整除,又能被9整除;
(3) x∈{x|x>0},x+ ≥2.
解 (1)可以改写为“平面内,所有凸多边形的外角和都等于360°”,故是全称量词命题,是真命题.
(2)命题中含有存在量词“至少有一个”,因此是存在量词命题,是真命题.
(3)命题中含有全称量词“ ”,是全称量词命题,是真命题.
典例剖析
题型一 全称量词命题与存在量词命题的辨析及真假判断
1.判断命题是全称量词命题还是存在量词命题的方法
(1)分析命题中是否含有量词;
(2)分析量词是全称量词还是存在量词;
(3)若命题中不含量词,要根据命题的意义去判断.
归纳总结
2.全称量词命题与存在量词命题真假的判断方法
(1)要判定全称量词命题“ x∈M,p(x)”是真命题,需要对集合M中每个元素x,证明p(x)都成立;如果在集合M中找到一个元素x,使得p(x)不成立,那么这个全称量词命题就是假命题.
(2)要判定存在量词命题“ x∈M,p(x)”是真命题,只需在集合M中找到一个元素x,使p(x)成立即可;如果在集合M中,使p(x)成立的元素x不存在,那么这个存在量词命题就是假命题.
归纳总结
1.以下四个命题既是存在量词命题又是真命题的是( )
A.锐角三角形的内角是锐角或钝角
B.至少有一个实数x,使x2≤0
C.两个无理数的和必是无理数
D.存在一个负数x,使 >2
B
练一练
例2.若命题p“ x∈R,2x2-3ax+9<0”为假命题,则实数a的取值范围是 .
解析 命题p的否定为“ x∈R,2x2-3ax+9≥0”,真命题.
典例剖析
题型二 由全称(存在)量词命题的真假确定参数的范围
应用全称(存在)量词命题求参数范围的两类题型
(1)全称量词命题的常见题型是“恒成立”问题,全称量词命题为真时,意味着命题对应的集合中的每一个元素都具有某种性质,所以可以利用代入体现集合中相应元素的具体性质中求解,也可以根据函数等数学知识来解决.
(2)存在量词命题的常见题型是以适合某种条件的结论“存在”“不存在”“是否存在”等语句表述.解答这类问题,一般要先对结论作出肯定存在的假设,然后从肯定的假设出发,结合已知条件进行推理证明,若推出合理的结论,则存在性随之解决;若导致矛盾,则否定了假设.
归纳总结
2.是否存在整数m,使得命题“ x≥- ,-5<3-4m若存在,求出m的值;若不存在,说明理由.
练一练
1.(2020广东广州期末)设命题p: x∈[0,1],都有x2-1≤0.则命题p的否定为( )
A. x∈[0,1],使x2-1≤0
B. x∈[0,1],使x2-1≥0
C. x∈[0,1],使x2-1>0
D. x∈[0,1],使x2-1>0
解析 根据全称量词命题的否定为存在量词命题,命题p: x∈[0,1],都有x2-1≤0的否定为 x∈[0,1],使x2-1>0.故选C.
C
随堂练
2.(2020山东滕州第一中学新校高一月考)设命题p: k∈N,k2>2k+3,则命题p的否定为( )
A. k∈N,k2>2k+3
B. k∈N,k2<2k+3
C. k∈N,k2≤2k+3
D. k∈N,k2≤2k+3
随堂练
解析 因为命题p: k∈N,k2>2k+3,所以其否定为 k∈N,k2≤2k+3.故选C.
C
3.(2020江苏南京外国语学校高一月考)下列命题为真命题的是( )
A. x∈Z,1<4x<3
B. x∈Z,15x+1=0
C. x∈R,x2-1=0
D. x∈R,x2+x+2>0
D
随堂练
4.已知命题:“ x∈[1,2],使x2+2x+a≥0”为真命题,则实数a的取值范围是 .
解析 当x∈[1,2]时,x2+2x=(x+1)2-1单调递增,
所以3≤x2+2x≤8,由题意可得a+8≥0,解得a≥-8.
随堂练
[-8,+∞)
5.判断下列命题是全称量词命题还是存在量词命题,并判断其真假.
(1)对某些实数x,有2x+1>0;
(2) x∈{3,5,7},3x+1是偶数;
(3) x∈Q,x2=3.
随堂练
解: (1)命题中含有存在量词“某些”,因此是存在量词命题,真命题.
(2)命题中含有全称量词的符号“ ”,因此是全称量词命题.
把3,5,7分别代入3x+1,得10,16,22,都是偶数,因此,该命题是真命题.
(3)命题中含有存在量词的符号“ ”,因此是存在量词命题.
由于使x2=3成立的实数只有± ,且它们都不是有理数,故没有一个有理数的平方等于3,所以该命题是假命题.
随堂练
1. 判断下列命题是全称量词命题还是存在量词命题:
(1) 任何实数的平方都是非负数;
(2) 任何数与0相乘,都等于0;
任何实数指都是,故是全称命题;
任何实数指都是,故是全称命题;
课本练习
(3) 任何一个实数都有相反数;
(4) 有些三角形的三个内角都是锐角.
任何实数指都是,故是全称命题;
有些是指存在的,故是存在性命题.
课本练习
2. 判断下列命题的真假:
(1) 任意一个平行四边形对边都相等;
(2) 有的四边形既是矩形又是菱形;
因为平行四边形的对边相等,所以任意一个平行四边形对边都相等是正确的,所以是真命题.
正方形既是矩形又是菱形,所以是真命题.
课本练习
(3) 实系数方程都有实数解;
(4) 有的正数比它的倒数小.
实系数方程 x2+1=0没有实数解,所以是假命题;
课本练习
错因分析
易错点 不能正确理解全称量词与存在量词的概念而致错
判断下列命题是全称量词命题还是存在量词命题.
(1)矩形有一个外接圆;
(2)非负实数有两个平方根;
(3)有一对实数(x,y),使2x-y+1<0成立.
解:
(1)可以改写为“所有的矩形都有一个外接圆”,是全称量词命题.
(2)可以改写为“所有的非负实数都有两个平方根”,是全称量词命题.
(3)可以改写为“ x∈R,y∈R,使2x-y+1<0成立”,是存在量词命题.
一、选择题
1.下列命题中存在量词命题的个数是( )
①有些自然数是偶数;②正方形是菱形;③能被6整除的数也能被3整除;
④对于任意x∈R,总有|x|≥0.
A.0 B.1 C.2 D.3
B
解析:命题①含有存在量词;命题②可以叙述为“所有的正方形都是菱形”,是全称量词命题;命题③可以叙述为“一切能被6整除的数也都能被3整除”,是全称量词命题;而命题④是全称量词命题,故有一个存在量词命题.
分层练习-基础
2.已知命题p: x∈R,x2+4x+a=0,若命题p是假命题,则实数a的取值范围是( )
A.(0,4) B.(4,+∞) C.(-∞,0) D.[4,+∞)
解析 ∵p是假命题,
∴方程x2+4x+a=0没有实数根,
即Δ=16-4a<0,即a>4.
B
分层练习-基础
3.下列命题不是“ x∈R,x2>3”的表述方法的是( )
A.有一个x∈R,使得x2>3成立
B.对有些x∈R,使得x2>3成立
C.任选一个x∈R,都有x2>3成立
D.至少有一个x∈R,使得x2>3成立
解析:“任选一个”“任意一个”是全称量词.
C
分层练习-基础
A
4.将命题“x2+y2≥2xy”改写成全称量词命题为( )
A.对任意x,y∈R,都有x2+y2≥2xy成立
B.存在x,y∈R,使x2+y2≥2xy成立
C.对任意x>0,y>0,都有x2+y2≥2xy成立
D.存在x<0,y<0,使x2+y2≤2xy成立
解析:B,D有存在量词“存在”,
C中,x,y的范围与原命题不符.
分层练习-基础
5.(多选题)下列命题中的真命题是( )
ACD
解析:A项,∵x∈R,∴|x|+1>0,故A正确;
B项,∵x∈N*,∴当x=1时,(x-1)2=0与(x-1)2>0矛盾,故B错误;
D项,当x=1时,5x-3=2,故D正确.
分层练习-基础
二、填空题
6.命题“有些负数满足不等式(1+x)(1-9x)2>0”用“ ”写成存在量词命题为__________________________.
解析:存在量词命题“存在M中的元素x,使p(x)成立”可用符号简记为“ x∈M,p(x)”.
x<0,(1+x)(1-9x)2>0
分层练习-基础
7.若命题“ x∈R,使x2+2x-3m=0”为真命题,则实数m的取值范围为
________________.
解析 由方程有实根,即Δ=4+12m≥0,
分层练习-基础
8.下列全称量词命题中真命题的个数为________.
① x∈R,x2+2>0;
② x∈N,x4≥1;
③对任意x,y,都有x2+y2≠0.
1
解析:①由于 x∈R,都有x2≥0,因而有x2+2≥2>0,即x2+2>0,
所以命题“ x∈R,x2+2>0”是真命题.
②由于0∈N,当x=0时,x4≥1不成立,所以命题“ x∈N,x4≥1”是假命题.
③当x=y=0时,x2+y2=0,所以是假命题.
分层练习-基础
三、解答题
9.判断下列命题是全称量词命题还是存在量词命题?
(1)矩形有一个外接圆.
(2)非负实数有两个平方根.
(3)方程x2-x+1=0有实数根.
解 (1)原命题可改写为“所有的矩形都有一个外接圆”,是全称量词命题.
(2)原命题可改写为“任意的非负实数都有两个平方根”,是全称量词命题.
(3)原命题可改写为“存在实数x,使x2-x+1=0”,是存在量词命题.
分层练习-巩固
10.用量词符号“ ”“ ”表示下列命题,并判断其真假.
(1)实数都能写成分数形式;
解:(1) x∈R,x能写成分数形式.因为无理数不能写成分数形式,
所以该命题是假命题.
分层练习-巩固
(3)平行四边形的对角线互相平分;
(4)至少有一个集合A,满足A?{1,2,3}.
解:(3) x∈{x|x是平行四边形},x的对角线互相平分.
由平行四边形的性质可知此命题是真命题.
(4) A∈{A|A是集合},A?{1,2,3}.
例如存在A={3},使A?{1,2,3}成立,所以该命题是真命题.
分层练习-巩固
11.已知命题p: x≥3,使2x-15
解析:命题p为假命题,则任意x≥3,2x-1因为当x≥3时,2x-1≥5,故m≤5.
分层练习-巩固
12.(多选题)已知a>0,函数y=ax2+bx+c,实数m满足关于x的方程2ax+b=0,当x=m时的函数值记为M,则下列选项中的命题为真命题的是( )
A. x∈R,ax2+bx+c≤M B. x∈R,ax2+bx+c≥M
C. x∈R,ax2+bx+c≤M D. x∈R,ax2+bx+c≥M
ABD
分层练习-巩固
13.若 x∈R,函数y=mx2+x-m-a的图象和x轴恒有公共点,求实数a的取值范围.
解 (1)当m=0时,y=x-a与x轴恒有公共点,所以a∈R.
(2)当m≠0时,二次函数y=mx2+x-m-a的图象和x轴恒有公共点的充要条件是Δ=1+4m(m+a)≥0恒成立,即4m2+4am+1≥0恒成立.
设y1=4m2+4am+1,则可转化为此关于m的二次函数的图象恒在m轴上方(或图象顶点在m轴上)的充要条件是Δ1=(4a)2-16≤0,可得-1≤a≤1.
综上所述,当m=0时,a∈R;
当m≠0时,a∈{a|-1≤a≤1}.
分层练习-巩固
14.已知命题p:存在实数x∈R,使得ax2+2x-1=0成立.若命题p为真命题,求实数a的取值范围.
解 当a=0时,方程2x-1=0显然有解,符合题意;
当a≠0时,由题意可知Δ=4+4a≥0,∴a≥-1且a≠0.
综上a的取值范围为[-1,+∞).
分层练习-巩固
15.已知函数y=x2-2x+5.
(1)是否存在实数m,使不等式m+y>0对于任意x∈R恒成立,并说明理由;
(2)若存在一个实数x,使不等式m-y>0成立,求实数m的取值范围.
分层练习-拓展
全称(存在)量词命题在不等式中的应用
解 (1)存在.不等式m+y>0可化为m>-y,即m>-x2+2x-5=-(x-1)2-4.
要使m>-(x-1)2-4对于任意x∈R恒成立,只需m>-4即可.
故存在实数m,使不等式m+y>0对于任意x∈R恒成立,且m>-4.
(2)不等式m-y>0可化为m>y,若存在一个实数x,使不等式m>y成立,只需m>ymin.
又y=(x-1)2+4,∴ymin=4,则m>4.
故实数m的取值范围是(4,+∞).
分层练习-拓展
一般地,对任意的实数x,a>y恒成立,只要a>ymax;
若存在一个实数x,使a>y成立,只需a>ymin.
课堂小结
1.理解2个概念
(1)全称量词命题.
(2)存在量词命题.
2.掌握3种方法
(1)判断命题是全称量词命题还是存在量词命题,主要是看命题中是否含有全称量词或存在量词,有些全称量词命题不含全称量词,可以根据命题涉及的意义去判断.
(2)要确定一个全称量词命题是真命题,需保证该命题对所有的元素都成立;若能举出一个反例说明命题不成立,则该全称量词命题是假命题.
(3)要确定一个存在量词命题是真命题,举出一个例子说明该命题成立即可;若经过逻辑推理得到命题对所有的元素都不成立,则该存在量词命题是假命题.
课堂小结
全程量词命题与存在量词命题
全程量词
存在量词
全程量词命题
全程量词命题
苏教版2019高一数学(必修一)第一章 集合
2.3.2 全程量词命题与存在量词命题
学习目标
1.理解全称量词与存在量词的意义.
2.会判断命题是全称量词命题还是存在量词命题,
并会判断它的真假.(重点)
3.用全称量词、存在量词梳理、表达学过的相应数学内容,
重点提升数学抽象、逻辑推理素养.(难点)
情景导入
在某个城市中有一位理发师,他的广告词是这样写的:
“本人的理发技艺十分高超,誉满全城.我将为本城所有不给自己刮脸的人刮脸,我也只给这些人刮脸.我对各位表示热诚欢迎!”
来找他刮脸的人络绎不绝,这些人自然都是那些不给自己刮脸的人.
可是,有一天,这位理发师从镜子里看见自己的胡子长了,他本能地抓起了剃刀.
你们觉得他能不能给自己刮脸呢
如果他不给自己刮脸,他就属于“不给自己刮脸的人”,他就要给自己刮脸.而如果他给自己刮脸,他又属于“给自己刮脸的人”,他就不该给自己刮脸.
这就是著名的“罗素理发师悖论”问题,如果我们学习了全称量词命题与存在量词命题的知识,就可以通过逻辑推理方法进行分析了.
在日常生活和学习中,我们经常遇到这样的语句:
(1)对任意实数 x,都有 x >0;
(2)存在有理数x,使x -2=0;
(3)有的矩形是菱形;
(4)所有的质数都是奇数;
(5)有一个素数是偶数.
这些语句中用到了“任意”“存在”“有的”等词,它们表示什么含义?
1.全称量词与存在量词
新知探究
语句(1)使用了“任意”,
表示对每一个实数x,必定有“x ≥0”,
即没有使“x ≥0”不成立的实数x存在.
语句(2)使用了“存在”,
表示至少可以找到一个有理数 x,使“x —2 = 0”成立.
语句(3)使用了“有的”,
表示可以找到一个矩形,它是菱形.
语句(4)使用了“所有”,
表示每一个质数都是奇数.
全称量词与存在量词
全称量词 存在量词
量词 “所有”“________”
“每一个”等表示________的词 “存在”“_______” “有一个”等表示_______或_______的词
符号 用“_______”表示“对任意 x” 用“_______”表示“存在 x”
任意
全体
有的
部分
个体
x
x
概念归纳
例如:
上面的语句(1)可以表示为“ ∈R,x ≥ 0”,
即“任意实数的平方都不小于 0”.
上面的语句(2)可以表示为“ x∈Q,x —2=0”,
即“方程x -2 =0 存在有理数解”.
那么你知道常见的全称量词、存在量词还有哪些
答:(答案不唯一)
常见的全称量词还有“一切”“任给”“凡是”等.
常见的存在量词还有“有些”“对某些”“有的”等.
想一想
(1) 定义和表示方法:
全称量词命题 存在量词命题
定义 含有_________的命题称为全称量词命题 含有_________的命题称为存在量词命题
表示 一般形式可表示为:____________ 一般形式可表示为:____________
全称量词
存在量词
x∈M,p(x)
x∈M,p(x)
2.全称量词命题与存在量词命题
新知探究
(2) 本质:
全称量词的含义是“任意性”,存在量词的含义是“存在性”.
(3) 应用:
全称量词、存在量词是数学和日常生活中使用频率很高的一种逻辑用语,数学中存在大量的全称量词命题和存在量词命题.
概念归纳
全称量词命题中的“x,M与p(x)”表达的含义分别是什么
答:元素x可以表示实数、方程、函数、不等式,也可以表示几何图形,
相应的集合M是这些元素的某一特定的范围,
p(x)表示集合M的所有元素满足的性质,也可以用q(x),r(x)等符号表示.
想一想
判断下列命题的真假:
课本例1
解:因为对任意实数x,都有 x2≥0 ,
所以对任意实数x,都有 x2+2≥2>0,
即对任意实数x,都有 x2+2>0 成立,
因此,“ x∈R,x2+2>0”是真命题.
由例1我们发现:
要判定一个存在量词命题为真,只要在给定的集合中找到一个元素,使命题为真即可;否则命题为假.
要判定一个全称量词命题为真,必须对给定的集合中的每一个元素,命题都为真;但要判定一个全称量词命题为假,只要在给定的集合中找到一个元素,使命题为假.
概念归纳
给定的集合对存在量词命题、全称量词命题的真假有没有影响
试举例说明.
思考探究
例 1.判断下列命题是全称量词命题还是存在量词命题,并判断其真假.
(1)平面内,凸多边形的外角和等于360° ;
(2)至少有一个整数,它既能被11整除,又能被9整除;
(3) x∈{x|x>0},x+ ≥2.
解 (1)可以改写为“平面内,所有凸多边形的外角和都等于360°”,故是全称量词命题,是真命题.
(2)命题中含有存在量词“至少有一个”,因此是存在量词命题,是真命题.
(3)命题中含有全称量词“ ”,是全称量词命题,是真命题.
典例剖析
题型一 全称量词命题与存在量词命题的辨析及真假判断
1.判断命题是全称量词命题还是存在量词命题的方法
(1)分析命题中是否含有量词;
(2)分析量词是全称量词还是存在量词;
(3)若命题中不含量词,要根据命题的意义去判断.
归纳总结
2.全称量词命题与存在量词命题真假的判断方法
(1)要判定全称量词命题“ x∈M,p(x)”是真命题,需要对集合M中每个元素x,证明p(x)都成立;如果在集合M中找到一个元素x,使得p(x)不成立,那么这个全称量词命题就是假命题.
(2)要判定存在量词命题“ x∈M,p(x)”是真命题,只需在集合M中找到一个元素x,使p(x)成立即可;如果在集合M中,使p(x)成立的元素x不存在,那么这个存在量词命题就是假命题.
归纳总结
1.以下四个命题既是存在量词命题又是真命题的是( )
A.锐角三角形的内角是锐角或钝角
B.至少有一个实数x,使x2≤0
C.两个无理数的和必是无理数
D.存在一个负数x,使 >2
B
练一练
例2.若命题p“ x∈R,2x2-3ax+9<0”为假命题,则实数a的取值范围是 .
解析 命题p的否定为“ x∈R,2x2-3ax+9≥0”,真命题.
典例剖析
题型二 由全称(存在)量词命题的真假确定参数的范围
应用全称(存在)量词命题求参数范围的两类题型
(1)全称量词命题的常见题型是“恒成立”问题,全称量词命题为真时,意味着命题对应的集合中的每一个元素都具有某种性质,所以可以利用代入体现集合中相应元素的具体性质中求解,也可以根据函数等数学知识来解决.
(2)存在量词命题的常见题型是以适合某种条件的结论“存在”“不存在”“是否存在”等语句表述.解答这类问题,一般要先对结论作出肯定存在的假设,然后从肯定的假设出发,结合已知条件进行推理证明,若推出合理的结论,则存在性随之解决;若导致矛盾,则否定了假设.
归纳总结
2.是否存在整数m,使得命题“ x≥- ,-5<3-4m
练一练
1.(2020广东广州期末)设命题p: x∈[0,1],都有x2-1≤0.则命题p的否定为( )
A. x∈[0,1],使x2-1≤0
B. x∈[0,1],使x2-1≥0
C. x∈[0,1],使x2-1>0
D. x∈[0,1],使x2-1>0
解析 根据全称量词命题的否定为存在量词命题,命题p: x∈[0,1],都有x2-1≤0的否定为 x∈[0,1],使x2-1>0.故选C.
C
随堂练
2.(2020山东滕州第一中学新校高一月考)设命题p: k∈N,k2>2k+3,则命题p的否定为( )
A. k∈N,k2>2k+3
B. k∈N,k2<2k+3
C. k∈N,k2≤2k+3
D. k∈N,k2≤2k+3
随堂练
解析 因为命题p: k∈N,k2>2k+3,所以其否定为 k∈N,k2≤2k+3.故选C.
C
3.(2020江苏南京外国语学校高一月考)下列命题为真命题的是( )
A. x∈Z,1<4x<3
B. x∈Z,15x+1=0
C. x∈R,x2-1=0
D. x∈R,x2+x+2>0
D
随堂练
4.已知命题:“ x∈[1,2],使x2+2x+a≥0”为真命题,则实数a的取值范围是 .
解析 当x∈[1,2]时,x2+2x=(x+1)2-1单调递增,
所以3≤x2+2x≤8,由题意可得a+8≥0,解得a≥-8.
随堂练
[-8,+∞)
5.判断下列命题是全称量词命题还是存在量词命题,并判断其真假.
(1)对某些实数x,有2x+1>0;
(2) x∈{3,5,7},3x+1是偶数;
(3) x∈Q,x2=3.
随堂练
解: (1)命题中含有存在量词“某些”,因此是存在量词命题,真命题.
(2)命题中含有全称量词的符号“ ”,因此是全称量词命题.
把3,5,7分别代入3x+1,得10,16,22,都是偶数,因此,该命题是真命题.
(3)命题中含有存在量词的符号“ ”,因此是存在量词命题.
由于使x2=3成立的实数只有± ,且它们都不是有理数,故没有一个有理数的平方等于3,所以该命题是假命题.
随堂练
1. 判断下列命题是全称量词命题还是存在量词命题:
(1) 任何实数的平方都是非负数;
(2) 任何数与0相乘,都等于0;
任何实数指都是,故是全称命题;
任何实数指都是,故是全称命题;
课本练习
(3) 任何一个实数都有相反数;
(4) 有些三角形的三个内角都是锐角.
任何实数指都是,故是全称命题;
有些是指存在的,故是存在性命题.
课本练习
2. 判断下列命题的真假:
(1) 任意一个平行四边形对边都相等;
(2) 有的四边形既是矩形又是菱形;
因为平行四边形的对边相等,所以任意一个平行四边形对边都相等是正确的,所以是真命题.
正方形既是矩形又是菱形,所以是真命题.
课本练习
(3) 实系数方程都有实数解;
(4) 有的正数比它的倒数小.
实系数方程 x2+1=0没有实数解,所以是假命题;
课本练习
错因分析
易错点 不能正确理解全称量词与存在量词的概念而致错
判断下列命题是全称量词命题还是存在量词命题.
(1)矩形有一个外接圆;
(2)非负实数有两个平方根;
(3)有一对实数(x,y),使2x-y+1<0成立.
解:
(1)可以改写为“所有的矩形都有一个外接圆”,是全称量词命题.
(2)可以改写为“所有的非负实数都有两个平方根”,是全称量词命题.
(3)可以改写为“ x∈R,y∈R,使2x-y+1<0成立”,是存在量词命题.
一、选择题
1.下列命题中存在量词命题的个数是( )
①有些自然数是偶数;②正方形是菱形;③能被6整除的数也能被3整除;
④对于任意x∈R,总有|x|≥0.
A.0 B.1 C.2 D.3
B
解析:命题①含有存在量词;命题②可以叙述为“所有的正方形都是菱形”,是全称量词命题;命题③可以叙述为“一切能被6整除的数也都能被3整除”,是全称量词命题;而命题④是全称量词命题,故有一个存在量词命题.
分层练习-基础
2.已知命题p: x∈R,x2+4x+a=0,若命题p是假命题,则实数a的取值范围是( )
A.(0,4) B.(4,+∞) C.(-∞,0) D.[4,+∞)
解析 ∵p是假命题,
∴方程x2+4x+a=0没有实数根,
即Δ=16-4a<0,即a>4.
B
分层练习-基础
3.下列命题不是“ x∈R,x2>3”的表述方法的是( )
A.有一个x∈R,使得x2>3成立
B.对有些x∈R,使得x2>3成立
C.任选一个x∈R,都有x2>3成立
D.至少有一个x∈R,使得x2>3成立
解析:“任选一个”“任意一个”是全称量词.
C
分层练习-基础
A
4.将命题“x2+y2≥2xy”改写成全称量词命题为( )
A.对任意x,y∈R,都有x2+y2≥2xy成立
B.存在x,y∈R,使x2+y2≥2xy成立
C.对任意x>0,y>0,都有x2+y2≥2xy成立
D.存在x<0,y<0,使x2+y2≤2xy成立
解析:B,D有存在量词“存在”,
C中,x,y的范围与原命题不符.
分层练习-基础
5.(多选题)下列命题中的真命题是( )
ACD
解析:A项,∵x∈R,∴|x|+1>0,故A正确;
B项,∵x∈N*,∴当x=1时,(x-1)2=0与(x-1)2>0矛盾,故B错误;
D项,当x=1时,5x-3=2,故D正确.
分层练习-基础
二、填空题
6.命题“有些负数满足不等式(1+x)(1-9x)2>0”用“ ”写成存在量词命题为__________________________.
解析:存在量词命题“存在M中的元素x,使p(x)成立”可用符号简记为“ x∈M,p(x)”.
x<0,(1+x)(1-9x)2>0
分层练习-基础
7.若命题“ x∈R,使x2+2x-3m=0”为真命题,则实数m的取值范围为
________________.
解析 由方程有实根,即Δ=4+12m≥0,
分层练习-基础
8.下列全称量词命题中真命题的个数为________.
① x∈R,x2+2>0;
② x∈N,x4≥1;
③对任意x,y,都有x2+y2≠0.
1
解析:①由于 x∈R,都有x2≥0,因而有x2+2≥2>0,即x2+2>0,
所以命题“ x∈R,x2+2>0”是真命题.
②由于0∈N,当x=0时,x4≥1不成立,所以命题“ x∈N,x4≥1”是假命题.
③当x=y=0时,x2+y2=0,所以是假命题.
分层练习-基础
三、解答题
9.判断下列命题是全称量词命题还是存在量词命题?
(1)矩形有一个外接圆.
(2)非负实数有两个平方根.
(3)方程x2-x+1=0有实数根.
解 (1)原命题可改写为“所有的矩形都有一个外接圆”,是全称量词命题.
(2)原命题可改写为“任意的非负实数都有两个平方根”,是全称量词命题.
(3)原命题可改写为“存在实数x,使x2-x+1=0”,是存在量词命题.
分层练习-巩固
10.用量词符号“ ”“ ”表示下列命题,并判断其真假.
(1)实数都能写成分数形式;
解:(1) x∈R,x能写成分数形式.因为无理数不能写成分数形式,
所以该命题是假命题.
分层练习-巩固
(3)平行四边形的对角线互相平分;
(4)至少有一个集合A,满足A?{1,2,3}.
解:(3) x∈{x|x是平行四边形},x的对角线互相平分.
由平行四边形的性质可知此命题是真命题.
(4) A∈{A|A是集合},A?{1,2,3}.
例如存在A={3},使A?{1,2,3}成立,所以该命题是真命题.
分层练习-巩固
11.已知命题p: x≥3,使2x-1
解析:命题p为假命题,则任意x≥3,2x-1
分层练习-巩固
12.(多选题)已知a>0,函数y=ax2+bx+c,实数m满足关于x的方程2ax+b=0,当x=m时的函数值记为M,则下列选项中的命题为真命题的是( )
A. x∈R,ax2+bx+c≤M B. x∈R,ax2+bx+c≥M
C. x∈R,ax2+bx+c≤M D. x∈R,ax2+bx+c≥M
ABD
分层练习-巩固
13.若 x∈R,函数y=mx2+x-m-a的图象和x轴恒有公共点,求实数a的取值范围.
解 (1)当m=0时,y=x-a与x轴恒有公共点,所以a∈R.
(2)当m≠0时,二次函数y=mx2+x-m-a的图象和x轴恒有公共点的充要条件是Δ=1+4m(m+a)≥0恒成立,即4m2+4am+1≥0恒成立.
设y1=4m2+4am+1,则可转化为此关于m的二次函数的图象恒在m轴上方(或图象顶点在m轴上)的充要条件是Δ1=(4a)2-16≤0,可得-1≤a≤1.
综上所述,当m=0时,a∈R;
当m≠0时,a∈{a|-1≤a≤1}.
分层练习-巩固
14.已知命题p:存在实数x∈R,使得ax2+2x-1=0成立.若命题p为真命题,求实数a的取值范围.
解 当a=0时,方程2x-1=0显然有解,符合题意;
当a≠0时,由题意可知Δ=4+4a≥0,∴a≥-1且a≠0.
综上a的取值范围为[-1,+∞).
分层练习-巩固
15.已知函数y=x2-2x+5.
(1)是否存在实数m,使不等式m+y>0对于任意x∈R恒成立,并说明理由;
(2)若存在一个实数x,使不等式m-y>0成立,求实数m的取值范围.
分层练习-拓展
全称(存在)量词命题在不等式中的应用
解 (1)存在.不等式m+y>0可化为m>-y,即m>-x2+2x-5=-(x-1)2-4.
要使m>-(x-1)2-4对于任意x∈R恒成立,只需m>-4即可.
故存在实数m,使不等式m+y>0对于任意x∈R恒成立,且m>-4.
(2)不等式m-y>0可化为m>y,若存在一个实数x,使不等式m>y成立,只需m>ymin.
又y=(x-1)2+4,∴ymin=4,则m>4.
故实数m的取值范围是(4,+∞).
分层练习-拓展
一般地,对任意的实数x,a>y恒成立,只要a>ymax;
若存在一个实数x,使a>y成立,只需a>ymin.
课堂小结
1.理解2个概念
(1)全称量词命题.
(2)存在量词命题.
2.掌握3种方法
(1)判断命题是全称量词命题还是存在量词命题,主要是看命题中是否含有全称量词或存在量词,有些全称量词命题不含全称量词,可以根据命题涉及的意义去判断.
(2)要确定一个全称量词命题是真命题,需保证该命题对所有的元素都成立;若能举出一个反例说明命题不成立,则该全称量词命题是假命题.
(3)要确定一个存在量词命题是真命题,举出一个例子说明该命题成立即可;若经过逻辑推理得到命题对所有的元素都不成立,则该存在量词命题是假命题.
课堂小结
全程量词命题与存在量词命题
全程量词
存在量词
全程量词命题
全程量词命题
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
