苏教版高中数学必修第一册第6章幂函数、指数函数和对数函数6.2指数函数(第一课时指数函数的图象与性质)教学课件(共38张PPT)
文档属性
| 名称 | 苏教版高中数学必修第一册第6章幂函数、指数函数和对数函数6.2指数函数(第一课时指数函数的图象与性质)教学课件(共38张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览











文档简介
(共38张PPT)
6.2 指数函数(第一课时)
指数函数的图象与性质
课标要求 素养要求
1.了解指数函数的实际背景,理解指数函数的概念.
2.掌握指数函数的图象及简单性质.
3.会用指数函数的图象与性质解决问题. 通过指数函数的图象及性质的理解与应用,提升直观想象素养、逻辑推理素养和数学抽象素养.
新知探究
将一张报纸连续对折,折叠次数x与对应的层数y间存在什么关系?对折后的面积S(设原面积为1)与折叠的次数有怎样的关系?
提示 (1)幂的形式;(2)幂的底数是一个大于0且不等于1的常数;(3)幂的指数是一个变量.
1.指数函数的概念
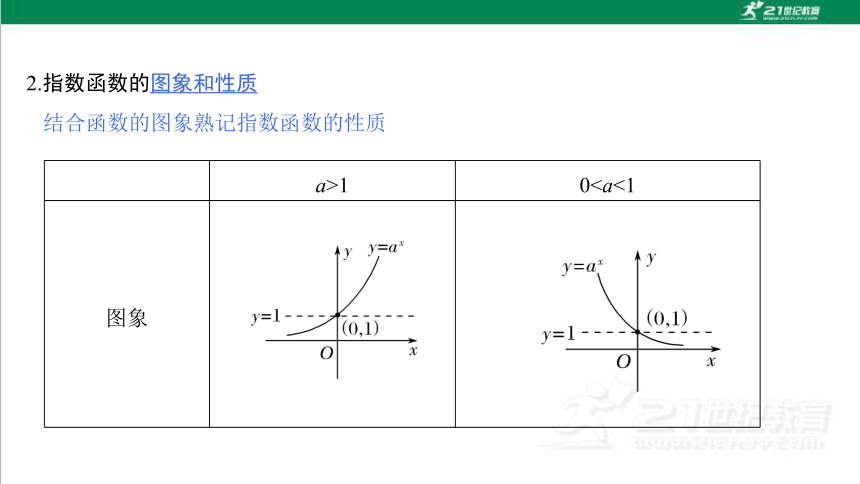
2.指数函数的图象和性质
结合函数的图象熟记指数函数的性质
a>1 0图象
(0,+∞)
(0,1)
00y>1
减函数
R
基础自测
[判断题]
1.函数y=2x+1是指数函数.( )
提示 因为指数不是x,所以函数y=2x+1不是指数函数.
2.函数y=(-5)x是指数函数.( )
提示 因为底数小于0,所以函数y=(-5)x不是指数函数.
3.y=ax(a>0且a≠1)的最小值为0.( )
提示 因为指数函数的图象都在x轴上方,值域为(0,+∞),没有最小值.
×
×
×
[基础训练]
1.下列函数中一定是指数函数的是( )
答案 B
2.函数y=2-x的图象是( )
答案 B
3.若函数f(x)是指数函数,且f(2)=2,则f(x)=________.
[思考题]
1.为什么规定指数函数的底数a>0且a≠1
提示 规定y=ax中a>0,且a≠1的理由:①当a≤0时,ax可能无意义;②当a>0时,x可以取任何实数;③当a=1时,ax=1(x∈R),无研究价值.因此规定y=ax中a>0,且a≠1.
2.若x10且a≠1)大小关系如何?
提示 当a>1时,y=ax在R上为单调增函数.
所以ax1ax2.
题型一 指数函数的概念
【例1】 (1)给出下列函数:
①y=2·3x;②y=3x+1;③y=3x;④y=x3;⑤y=(-2)x.其中,指数函数的个数是( )
A.0 B.1 C.2 D.4
解析 (1)①中,3x的系数是2,故①不是指数函数;②中,y=3x+1的指数是x+1,不是自变量x,故②不是指数函数;③中,3x的系数是1,幂的指数是自变量x,且只有3x一项,故③是指数函数;④中,y=x3的底为自变量,指数为常数,故④不是指数函数.⑤中,底数-2<0,不是指数函数.
答案 (1)B (2)125
规律方法 1.指数函数的解析式必须具有三个特征:
(1)底数a为大于0且不等于1的常数;(2)指数位置是自变量x;(3)ax的系数是1.
2.求指数函数的关键是求底数a,并注意a的限制条件.
【训练1】 (1)若函数y=a2(2-a)x是指数函数,则( )
A.a=1或-1 B.a=1
C.a=-1 D.a>0且a≠1
(2)已知指数函数f(x)的图象过点(3,π),则函数f(x)的解析式为________.
题型二 指数函数的性质
角度1 函数过定点
【例2-1】 函数f(x)=2ax+1-3(a>0,且a≠1)的图象恒过的定点是________.
解析 因为y=ax的图象过定点(0,1),所以令x+1=0,即x=-1,则f(-1)=-1,故f(x)=2ax+1-3的图象过定点(-1,-1).
答案 (-1,-1)
角度2 函数的定义域、值域
【例2-2】 (1)若函数f(x)=2x+3,x∈[2,3],则函数f(x)的值域为________.
(2)函数f(x)=2-x-1的值域是________.
解析 (1)由题意知函数f(x)=2x+3在R上是增函数,且x∈[2,3],所以2x∈[4,8],故f(x)的值域为[7,11].
∴值域为(-1,+∞).
答案 (1)[7,11] (2)(-1,+∞)
角度3 由单调性比较大小
【例2-3】 比较下列各组数的大小:
规律方法 (1)抓住特殊点:指数函数的图象过定点(0,1),求指数型函数图象所过的定点时,只要令指数为0,求出对应的y的值,即可得函数图象所过的定点.
(2)合理利用指数型函数的单调性、图象的变化规律及中间值进行幂的大小判断.
(3)对于三个(或三个以上)数的大小比较,则应先根据特殊值0,1进行分组,再比较各组数的大小.
【训练2】 (1)函数y=a2x+1-4(a>0,且a≠1)的图象恒过点________,值域为________.
题型三 指数函数的图象变换
【例3】 画出下列函数的图象,并说明它们是由函数f(x)=2x的图象经过怎样的变换得到的.
(1)y=2x-1;(2)y=2x+1;(3)y=2|x|;
(4)y=|2x-1|;(5)y=-2x;(6)y=-2-x.
解 如图所示.
(1)y=2x-1的图象是由y=2x的图象向右平移1个单位长度得到的.
(2)y=2x+1的图象是由y=2x的图象向上平移1个单位长度得到的.
(3)y=2|x|的图象是由y=2x的y轴右侧的图象和其关于y轴对称的图象组成的,包括y轴上的(0,1)点.
(4)y=|2x-1|的图象是由y=2x的图象向下平移1个单位长度,然后将其x轴下方的图象翻折到x轴上方得到的.
(5)y=-2x的图象与y=2x的图象关于x轴对称.
(6)y=-2-x的图象与y=2x的图象关于原点对称.
规律方法 函数图象的变换规律
(1)平移变换:将函数y=f(x)的图象向右平移m(m>0)个单位长度得函数y=f(x-m)的图象(若m<0,就是向左平移|m|个单位长度),将函数y=f(x)的图象向上平移n(n>0)个单位长度,得到函数y=f(x)+n的图象(若n<0,就是向下平移|n|个单位长度).
(2)对称变换:
①函数y=f(x)的图象与函数y=f(-x)的图象关于y轴对称,函数y=f(x)的图象与函数y=-f(x)的图象关于x轴对称,函数y=f(x)的图象与函数y=-f(-x)的图象关于原点对称;
②函数y=f(|x|)是一个偶函数,其图象关于y轴对称,是将函数y=f(x)位于y轴右侧的图象保留(左侧的擦去),然后将y轴右侧的图象沿y轴对称到左侧,就得到函数y=f(|x|)的图象;
③函数y=|f(x)|的图象是将函数y=f(x)的图象在x轴下方的部分沿x轴翻折到上方,x轴上方的部分不变.
【训练3】 (1)如图是指数函数①y=ax;②y=bx;③y=cx;④y=dx的图象,则a,b,c,d与1的大小关系是( )
A.aC.1(2)函数f(x)=ax-b的图象如图所示,其中a,b为常数,则下列结论正确的是( )
A.a>1,b<0
B.a>1,b>0
C.00
D.0解析 (1)可先分两类,③④的底数大于1,①②的底数小于1,再由图象③④比较c,d的大小,由图象①②比较a,b的大小.在y轴右侧,当指数函数的底数大于1时,图象上升,且底数越大,图象越靠近y轴,当指数函数的底数大于0且小于1时,图象下降,且底数越小,图象越靠近x轴(即用x=1截图,底大图高),故选B.
(2)从曲线的变化趋势,可以得到函数f(x)为减函数,从而有00,即b<0(或令x=0得a-b<1即a-b0,即b<0).
答案 (1)B (2)D
一、课堂小结
1.通过指数函数的图象与性质的学习,提升数学直观想象素养、逻辑推理素养与数学抽象素养.
2.判断一个函数是不是指数函数,关键是看解析式是否符合y=ax(a>0且a≠1)这一结构形式,即ax的系数是1,指数是x且系数为1.
3.指数函数的图象与性质,要注意分a>1与0二、课堂检测
1.指数函数y=ax与y=bx的图象如图所示,则( )
A.a<0,b<0
B.a<0,b>0
C.01
D.0解析 结合指数函数图象的特点可知01.
答案 C
2.当x∈[-2,2)时,y=3-x-1的值域是( )
答案 A
3.函数f(x)=2·ax-1+1的图象恒过定点________.
解析 令x-1=0,得x=1,f(1)=2×1+1=3,所以f(x)的图象恒过定点(1,3).
答案 (1,3)
4.不等式23-2x<0.53x-4的解集为________.
解析 原不等式可化为23-2x<24-3x,因为函数y=2x是R上的增函数,所以3-2x<4-3x,解得x<1,则解集为{x|x<1}.
答案 {x|x<1}
5.比较下列各组值的大小:
(1)1.8-0.1,1.8-0.2;
(2)1.90.3,0.73.1;
(3)a1.3,a2.5(a>0,且a≠1).
解 (1)因为函数y=1.8x是R上的增函数,且-0.1>-0.2,所以1.8-0.1>1.8-0.2.
(2)因为1.90.3>1.90=1,0.73.1<0.70=1,
所以1.90.3>0.73.1.
(3)当a>1时,函数y=ax是R上的增函数,又1.3<2.5,故a1.3当0a2.5.
6.2 指数函数(第一课时)
指数函数的图象与性质
课标要求 素养要求
1.了解指数函数的实际背景,理解指数函数的概念.
2.掌握指数函数的图象及简单性质.
3.会用指数函数的图象与性质解决问题. 通过指数函数的图象及性质的理解与应用,提升直观想象素养、逻辑推理素养和数学抽象素养.
新知探究
将一张报纸连续对折,折叠次数x与对应的层数y间存在什么关系?对折后的面积S(设原面积为1)与折叠的次数有怎样的关系?
提示 (1)幂的形式;(2)幂的底数是一个大于0且不等于1的常数;(3)幂的指数是一个变量.
1.指数函数的概念
2.指数函数的图象和性质
结合函数的图象熟记指数函数的性质
a>1 0
(0,+∞)
(0,1)
0
减函数
R
基础自测
[判断题]
1.函数y=2x+1是指数函数.( )
提示 因为指数不是x,所以函数y=2x+1不是指数函数.
2.函数y=(-5)x是指数函数.( )
提示 因为底数小于0,所以函数y=(-5)x不是指数函数.
3.y=ax(a>0且a≠1)的最小值为0.( )
提示 因为指数函数的图象都在x轴上方,值域为(0,+∞),没有最小值.
×
×
×
[基础训练]
1.下列函数中一定是指数函数的是( )
答案 B
2.函数y=2-x的图象是( )
答案 B
3.若函数f(x)是指数函数,且f(2)=2,则f(x)=________.
[思考题]
1.为什么规定指数函数的底数a>0且a≠1
提示 规定y=ax中a>0,且a≠1的理由:①当a≤0时,ax可能无意义;②当a>0时,x可以取任何实数;③当a=1时,ax=1(x∈R),无研究价值.因此规定y=ax中a>0,且a≠1.
2.若x1
提示 当a>1时,y=ax在R上为单调增函数.
所以ax1
题型一 指数函数的概念
【例1】 (1)给出下列函数:
①y=2·3x;②y=3x+1;③y=3x;④y=x3;⑤y=(-2)x.其中,指数函数的个数是( )
A.0 B.1 C.2 D.4
解析 (1)①中,3x的系数是2,故①不是指数函数;②中,y=3x+1的指数是x+1,不是自变量x,故②不是指数函数;③中,3x的系数是1,幂的指数是自变量x,且只有3x一项,故③是指数函数;④中,y=x3的底为自变量,指数为常数,故④不是指数函数.⑤中,底数-2<0,不是指数函数.
答案 (1)B (2)125
规律方法 1.指数函数的解析式必须具有三个特征:
(1)底数a为大于0且不等于1的常数;(2)指数位置是自变量x;(3)ax的系数是1.
2.求指数函数的关键是求底数a,并注意a的限制条件.
【训练1】 (1)若函数y=a2(2-a)x是指数函数,则( )
A.a=1或-1 B.a=1
C.a=-1 D.a>0且a≠1
(2)已知指数函数f(x)的图象过点(3,π),则函数f(x)的解析式为________.
题型二 指数函数的性质
角度1 函数过定点
【例2-1】 函数f(x)=2ax+1-3(a>0,且a≠1)的图象恒过的定点是________.
解析 因为y=ax的图象过定点(0,1),所以令x+1=0,即x=-1,则f(-1)=-1,故f(x)=2ax+1-3的图象过定点(-1,-1).
答案 (-1,-1)
角度2 函数的定义域、值域
【例2-2】 (1)若函数f(x)=2x+3,x∈[2,3],则函数f(x)的值域为________.
(2)函数f(x)=2-x-1的值域是________.
解析 (1)由题意知函数f(x)=2x+3在R上是增函数,且x∈[2,3],所以2x∈[4,8],故f(x)的值域为[7,11].
∴值域为(-1,+∞).
答案 (1)[7,11] (2)(-1,+∞)
角度3 由单调性比较大小
【例2-3】 比较下列各组数的大小:
规律方法 (1)抓住特殊点:指数函数的图象过定点(0,1),求指数型函数图象所过的定点时,只要令指数为0,求出对应的y的值,即可得函数图象所过的定点.
(2)合理利用指数型函数的单调性、图象的变化规律及中间值进行幂的大小判断.
(3)对于三个(或三个以上)数的大小比较,则应先根据特殊值0,1进行分组,再比较各组数的大小.
【训练2】 (1)函数y=a2x+1-4(a>0,且a≠1)的图象恒过点________,值域为________.
题型三 指数函数的图象变换
【例3】 画出下列函数的图象,并说明它们是由函数f(x)=2x的图象经过怎样的变换得到的.
(1)y=2x-1;(2)y=2x+1;(3)y=2|x|;
(4)y=|2x-1|;(5)y=-2x;(6)y=-2-x.
解 如图所示.
(1)y=2x-1的图象是由y=2x的图象向右平移1个单位长度得到的.
(2)y=2x+1的图象是由y=2x的图象向上平移1个单位长度得到的.
(3)y=2|x|的图象是由y=2x的y轴右侧的图象和其关于y轴对称的图象组成的,包括y轴上的(0,1)点.
(4)y=|2x-1|的图象是由y=2x的图象向下平移1个单位长度,然后将其x轴下方的图象翻折到x轴上方得到的.
(5)y=-2x的图象与y=2x的图象关于x轴对称.
(6)y=-2-x的图象与y=2x的图象关于原点对称.
规律方法 函数图象的变换规律
(1)平移变换:将函数y=f(x)的图象向右平移m(m>0)个单位长度得函数y=f(x-m)的图象(若m<0,就是向左平移|m|个单位长度),将函数y=f(x)的图象向上平移n(n>0)个单位长度,得到函数y=f(x)+n的图象(若n<0,就是向下平移|n|个单位长度).
(2)对称变换:
①函数y=f(x)的图象与函数y=f(-x)的图象关于y轴对称,函数y=f(x)的图象与函数y=-f(x)的图象关于x轴对称,函数y=f(x)的图象与函数y=-f(-x)的图象关于原点对称;
②函数y=f(|x|)是一个偶函数,其图象关于y轴对称,是将函数y=f(x)位于y轴右侧的图象保留(左侧的擦去),然后将y轴右侧的图象沿y轴对称到左侧,就得到函数y=f(|x|)的图象;
③函数y=|f(x)|的图象是将函数y=f(x)的图象在x轴下方的部分沿x轴翻折到上方,x轴上方的部分不变.
【训练3】 (1)如图是指数函数①y=ax;②y=bx;③y=cx;④y=dx的图象,则a,b,c,d与1的大小关系是( )
A.a
A.a>1,b<0
B.a>1,b>0
C.0
D.0
(2)从曲线的变化趋势,可以得到函数f(x)为减函数,从而有0
答案 (1)B (2)D
一、课堂小结
1.通过指数函数的图象与性质的学习,提升数学直观想象素养、逻辑推理素养与数学抽象素养.
2.判断一个函数是不是指数函数,关键是看解析式是否符合y=ax(a>0且a≠1)这一结构形式,即ax的系数是1,指数是x且系数为1.
3.指数函数的图象与性质,要注意分a>1与0
1.指数函数y=ax与y=bx的图象如图所示,则( )
A.a<0,b<0
B.a<0,b>0
C.0
D.0
答案 C
2.当x∈[-2,2)时,y=3-x-1的值域是( )
答案 A
3.函数f(x)=2·ax-1+1的图象恒过定点________.
解析 令x-1=0,得x=1,f(1)=2×1+1=3,所以f(x)的图象恒过定点(1,3).
答案 (1,3)
4.不等式23-2x<0.53x-4的解集为________.
解析 原不等式可化为23-2x<24-3x,因为函数y=2x是R上的增函数,所以3-2x<4-3x,解得x<1,则解集为{x|x<1}.
答案 {x|x<1}
5.比较下列各组值的大小:
(1)1.8-0.1,1.8-0.2;
(2)1.90.3,0.73.1;
(3)a1.3,a2.5(a>0,且a≠1).
解 (1)因为函数y=1.8x是R上的增函数,且-0.1>-0.2,所以1.8-0.1>1.8-0.2.
(2)因为1.90.3>1.90=1,0.73.1<0.70=1,
所以1.90.3>0.73.1.
(3)当a>1时,函数y=ax是R上的增函数,又1.3<2.5,故a1.3
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
