苏教版高中数学必修第一册第6章幂函数、指数函数和对数函数6.3对数函数(第二课时)教学课件(共48张PPT)
文档属性
| 名称 | 苏教版高中数学必修第一册第6章幂函数、指数函数和对数函数6.3对数函数(第二课时)教学课件(共48张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览











文档简介
(共48张PPT)
6.3 对数函数(第二课时)
课标要求 素养要求
1.进一步理解对数函数的图象和性质.
2.能运用对数函数的图象和性质解决相关问题. 结合对数函数的图象理解反函数的概念,掌握对数型函数的有关性质,发展直观想象素养、数学抽象素养及数学运算素养.
新知探究
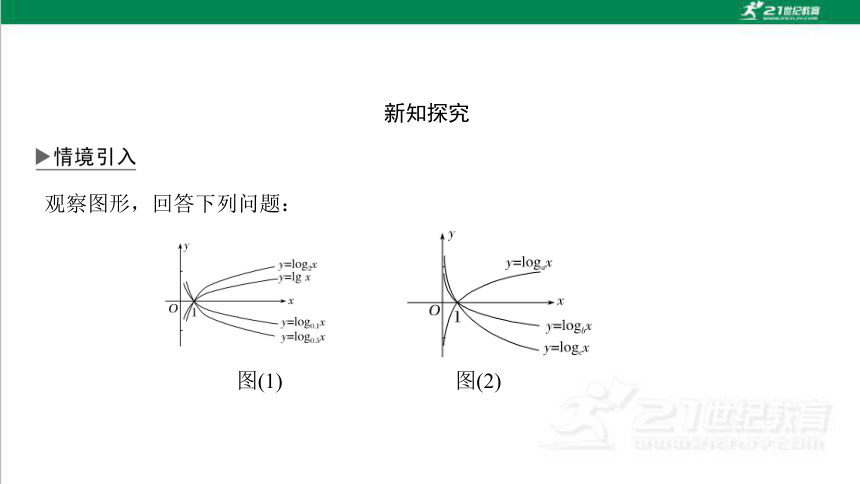
观察图形,回答下列问题:
图(1) 图(2)
问题 (1)观察图(1)所示的函数y=log2x,y=log0.5x,y=log10x,y=log0.1x图象,你能得出什么结论?
(2)函数y=logax,y=logbx,y=logcx的图象如图(2)所示,那么a,b,c的大小关系如何?
提示 (1)对于底数a>1的对数函数,在(1,+∞)内,底数越大越靠近x轴;对于底数0(2)由图象可知a>1,b,c都大于0且小于1,由于y=logbx的图象在(1,+∞)上比y=logcx的图象靠近x轴,所以b反函数
(1)当a>0,a≠1时,y=logax称为______的反函数,反之,y=ax也称为________的反函数.一般地,如果函数y=f(x)存在反函数,那么反函数记作____________.
(2)互为反函数的两个函数,图象关于y=x对称.
y=ax
y=logax
y=f-1(x)
基础自测
[判断题]
2.ln x<1的解集为(-∞,e).( )
提示 由ln x<1,解得03.y=ax与x=logay的图象相同(a>0且a≠1).( )
4.由函数y=log2x的图象向左平移1个单位可得y=log2x+1的图象.( )
提示 向左平移1个单位可得y=log2(x+1)的图象.
×
×
√
×
[基础训练]
2.已知log7(2x)解析 由0<2x答案 (0,2)
答案 (-∞,0)
[思考]
1.不同底的对数函数y=logax与y=logbx,a≠b的图象之间有何相对位置关系?
提示 作直线y=1,与各图象会有交点,底数越大,交点越靠右,简称“底大图右”.
2.y=ax与y=logax(a>0,a≠1)互为反函数,它们的性质有何关系?
提示 ①y=ax的定义域为y=logax的值域,y=ax的值域为y=logax的定义域.
②y=ax上任一点为(m,n),则点(n,m)必在其反函数y=logax的图象上,即互为反函数的两个函数的图象关于y=x对称.
③互为反函数的两个函数的单调性相同,但单调区间不一定相同.
题型一 对数函数的图象及应用
【例1】 (1)当a>1时,在同一坐标系中,函数y=a-x与y=logax的图象为( )
(2)已知f(x)=loga|x|,满足f(-5)=1,试画出函数f(x)的图象.
答案 C
对数函数y=logax在(0,+∞)上是增函数,过定点(1,0).故选C.
(2)解 ∵f(x)=loga|x|,
∴f(-5)=loga5=1,即a=5,
∴f(x)=log5|x|,
∴f(x)是偶函数,其图象如图所示.
【迁移1】 (变换条件)将本例(1)的条件“a>1”去掉,函数“y=logax”改为“y=loga(-x)”,则函数y=a-x与y=loga(-x)的图象可能是( )
解析 ∵在y=loga(-x)中,-x>0,∴x<0,
∴图象只能在y轴的左侧,故排除A,D;
当a>1时,y=loga(-x)是减函数,
答案 C
【迁移2】 (变换条件)将本例(2)中的函数改为f(x)=loga|x+1|,且满足f(-5)=1,求解析式并画其图象.
解 由f(-5)=loga|-5+1|=1得a=4,
即f(x)=log4|x+1|.
其图象画法:①先作y=log4x的图象,②将y=log4x的图象向左平移1个单位得y=log4(x+1)的图象,③再将y=log4(x+1)的图象关于x=-1对称,如图所示.
规律方法 有关对数函数图象间的变换规律
(1)一般地,函数y=f(x+a)+b(a,b为实数)的图象是由函数y=f(x)的图象沿x轴向左(a>0)或向右(a<0)平移|a|个单位长度,再沿y轴向上(b>0)或向下(b<0)平移|b|个单位长度得到的.
(2)含有绝对值的函数的图象是一种对称变换,一般地,y=f(|x-a|)的图象是关于直线x=a对称的轴对称图形;函数y=|f(x)|的图象与y=f(x)的图象在f(x)≥0的部分相同,在f(x)<0的部分关于x轴对称.
【训练1】 作出下列函数的大致图象:
(1)y=|log2x|;(2)y=|log2(x-1)|;
(3)y=|log2(1-x)|.
解 (1)第一步:作函数y=log2x的图象;
第二步:把函数y=log2x的图象位于x轴下方的部分沿x轴翻折(位于x轴和x轴上方的不变),即得y=|log2x|的图象(如图①).
(2)第一步和第二步同(1);
第三步:把y=|log2x|的图象向右平移1个单位长度即得y=|log2(x-1)|的图象(如图②).
(3)第一步:作函数y=log2x的图象;
第二步:把函数y=log2x的图象沿y轴翻折,
得y=log2(-x)的图象;
第三步:把y=log2(-x)的图象向右平移1个单位长度,得函数y=log2(1-x)的图象;
第四步:把y=log2(1-x)的图象位于x轴下方的部分沿x轴翻折(x轴上及x轴上方的不变),即得y=|log2(1-x)|的图象(如图③).
题型二 对数型函数的单调性
角度1 解对数不等式
【例2-1】 解下列不等式.
(2)因为log3x<1=log33,
所以原不等式的解集为{x|0所以原不等式的解集为{x|0当a>1时,函数y=logax在定义域内是增函数,
当0所以x2<1,所以-1因此函数的定义域为(-1,1).
令t=1-x2,x∈(-1,1).
单调递增区间为[0,1).
角度3 由单调性求参数
【例2-3】 (1)若函数f(x)=loga(6-ax)在[0,2]上为减函数,则a的取值范围是( )
A.(0,1) B.(1,3)
C.(1,3] D.[3,+∞)
解析 (1)函数由y=logau,u=6-ax复合而成,因为a>0,所以u=6-ax是减函数,那么函数y=logau就是增函数,所以a>1,因为[0,2]为定义域的子集,所以当x=2时,u=6-ax取得最小值,所以6-2a>0,解得a<3,所以1答案 (1)B (2)(-8,-6]
规律方法 1.对数不等式的三种类型及解法
(1)形如logax>logab的不等式,借助函数y=logax的单调性求解,如果a的取值不确定,需分a>1与0(2)形如logax>b的不等式,应将b化为以a为底数的对数的形式,再借助函数y=logax的单调性求解.
(3)形如logax>logbx的不等式,利用换底公式化为同底的对数进行求解或利用图象求解.
2.若a>1,则y=logaf(x)的单调性与y=f(x)的单调性相同,若0【训练2】 (1)已知log0.3(3x)答案 A
题型三 对数型函数性质的综合问题
角度1 值域问题
【例3-1】 求下列函数的值域.
(1)y=log2(x2-4x+6);
(2)y=log2(x2-4x-5).
解 (1)令u=x2-4x+6.∵x2-4x+6=(x-2)2+2≥2,
又f(x)=log2u在(0,+∞)上是增函数,∴log2(x2-4x+6)≥log22=1,
∴函数的值域是[1,+∞).
(2)∵x2-4x-5=(x-2)2-9≥-9,∴x2-4x-5能取到所有正实数,
∴函数y=log2(x2-4x-5)的值域是R.
角度2 奇偶性判断
所以f(-x)=-f(x),
角度3 综合应用
解得x>1或x<-1,故此函数的定义域为(-∞,-1)∪(1,+∞).
规律方法 (1)对于y=logaf(x)型函数,在函数定义域中确定t=f(x)的值域,再由y=logat的单调性确定函数的值域.
(2)含对数式的奇偶性判断,一般用f(x)±f(-x)=0来判断,运算相对简单.
【训练3】 已知f(x)=log4(4x-1).
(1)求f(x)的定义域;
(2)讨论f(x)的单调性;
解 (1)由4x-1>0,解得x>0,
因此f(x)的定义域为(0,+∞).
(2)设0因此log4(4x1-1)即f(x1)一、课堂小结
1.由对数函数的图象,反函数概念,研究对数型函数的性质,发展直观想象素养,数学抽象素养及数学运算素养.
2.比较两个对数值的大小及解对数不等式问题,其依据是对数函数的单调性.若对数的底数是字母且范围不明确,一般要分a>1和03.解决与对数函数相关的问题时要树立“定义域优先”的原则,同时注意数形结合思想和分类讨论思想在解决问题中的应用.
4.y=logaf(x)型函数性质的研究
(1)定义域:由f(x)>0解得x的取值范围,即为函数的定义域.
(2)值域:在函数y=logaf(x)的定义域中确定t=f(x)的值域,再由y=logat的单调性确定函数的值域.
(3)单调性:在定义域内考虑t=f(x)与y=logat的单调性,根据同增异减法则判定(或运用单调性定义判定).
(4)奇偶性:根据奇偶函数的定义判定.
(5)最值:在f(x)>0的条件下,确定t=f(x)的值域,再根据a确定函数y=logat的单调性,最后确定最值.
二、课堂检测
1.函数y=ax与y=-logax(a>0,且a≠1)在同一坐标系中的图象形状可能是( )
解析 函数y=-logax恒过定点(1,0),排除B;当a>1时,y=ax是增函数,y=-logax是减函数,当0答案 A
答案 D
3.已知f(x)=|log3x|,若f(a)>f(2),则a的取值范围为________.
解 设t=-x2+2x+1,则t=-(x-1)2+2.
6.3 对数函数(第二课时)
课标要求 素养要求
1.进一步理解对数函数的图象和性质.
2.能运用对数函数的图象和性质解决相关问题. 结合对数函数的图象理解反函数的概念,掌握对数型函数的有关性质,发展直观想象素养、数学抽象素养及数学运算素养.
新知探究
观察图形,回答下列问题:
图(1) 图(2)
问题 (1)观察图(1)所示的函数y=log2x,y=log0.5x,y=log10x,y=log0.1x图象,你能得出什么结论?
(2)函数y=logax,y=logbx,y=logcx的图象如图(2)所示,那么a,b,c的大小关系如何?
提示 (1)对于底数a>1的对数函数,在(1,+∞)内,底数越大越靠近x轴;对于底数0
(1)当a>0,a≠1时,y=logax称为______的反函数,反之,y=ax也称为________的反函数.一般地,如果函数y=f(x)存在反函数,那么反函数记作____________.
(2)互为反函数的两个函数,图象关于y=x对称.
y=ax
y=logax
y=f-1(x)
基础自测
[判断题]
2.ln x<1的解集为(-∞,e).( )
提示 由ln x<1,解得0
4.由函数y=log2x的图象向左平移1个单位可得y=log2x+1的图象.( )
提示 向左平移1个单位可得y=log2(x+1)的图象.
×
×
√
×
[基础训练]
2.已知log7(2x)
答案 (-∞,0)
[思考]
1.不同底的对数函数y=logax与y=logbx,a≠b的图象之间有何相对位置关系?
提示 作直线y=1,与各图象会有交点,底数越大,交点越靠右,简称“底大图右”.
2.y=ax与y=logax(a>0,a≠1)互为反函数,它们的性质有何关系?
提示 ①y=ax的定义域为y=logax的值域,y=ax的值域为y=logax的定义域.
②y=ax上任一点为(m,n),则点(n,m)必在其反函数y=logax的图象上,即互为反函数的两个函数的图象关于y=x对称.
③互为反函数的两个函数的单调性相同,但单调区间不一定相同.
题型一 对数函数的图象及应用
【例1】 (1)当a>1时,在同一坐标系中,函数y=a-x与y=logax的图象为( )
(2)已知f(x)=loga|x|,满足f(-5)=1,试画出函数f(x)的图象.
答案 C
对数函数y=logax在(0,+∞)上是增函数,过定点(1,0).故选C.
(2)解 ∵f(x)=loga|x|,
∴f(-5)=loga5=1,即a=5,
∴f(x)=log5|x|,
∴f(x)是偶函数,其图象如图所示.
【迁移1】 (变换条件)将本例(1)的条件“a>1”去掉,函数“y=logax”改为“y=loga(-x)”,则函数y=a-x与y=loga(-x)的图象可能是( )
解析 ∵在y=loga(-x)中,-x>0,∴x<0,
∴图象只能在y轴的左侧,故排除A,D;
当a>1时,y=loga(-x)是减函数,
答案 C
【迁移2】 (变换条件)将本例(2)中的函数改为f(x)=loga|x+1|,且满足f(-5)=1,求解析式并画其图象.
解 由f(-5)=loga|-5+1|=1得a=4,
即f(x)=log4|x+1|.
其图象画法:①先作y=log4x的图象,②将y=log4x的图象向左平移1个单位得y=log4(x+1)的图象,③再将y=log4(x+1)的图象关于x=-1对称,如图所示.
规律方法 有关对数函数图象间的变换规律
(1)一般地,函数y=f(x+a)+b(a,b为实数)的图象是由函数y=f(x)的图象沿x轴向左(a>0)或向右(a<0)平移|a|个单位长度,再沿y轴向上(b>0)或向下(b<0)平移|b|个单位长度得到的.
(2)含有绝对值的函数的图象是一种对称变换,一般地,y=f(|x-a|)的图象是关于直线x=a对称的轴对称图形;函数y=|f(x)|的图象与y=f(x)的图象在f(x)≥0的部分相同,在f(x)<0的部分关于x轴对称.
【训练1】 作出下列函数的大致图象:
(1)y=|log2x|;(2)y=|log2(x-1)|;
(3)y=|log2(1-x)|.
解 (1)第一步:作函数y=log2x的图象;
第二步:把函数y=log2x的图象位于x轴下方的部分沿x轴翻折(位于x轴和x轴上方的不变),即得y=|log2x|的图象(如图①).
(2)第一步和第二步同(1);
第三步:把y=|log2x|的图象向右平移1个单位长度即得y=|log2(x-1)|的图象(如图②).
(3)第一步:作函数y=log2x的图象;
第二步:把函数y=log2x的图象沿y轴翻折,
得y=log2(-x)的图象;
第三步:把y=log2(-x)的图象向右平移1个单位长度,得函数y=log2(1-x)的图象;
第四步:把y=log2(1-x)的图象位于x轴下方的部分沿x轴翻折(x轴上及x轴上方的不变),即得y=|log2(1-x)|的图象(如图③).
题型二 对数型函数的单调性
角度1 解对数不等式
【例2-1】 解下列不等式.
(2)因为log3x<1=log33,
所以原不等式的解集为{x|0
当0
令t=1-x2,x∈(-1,1).
单调递增区间为[0,1).
角度3 由单调性求参数
【例2-3】 (1)若函数f(x)=loga(6-ax)在[0,2]上为减函数,则a的取值范围是( )
A.(0,1) B.(1,3)
C.(1,3] D.[3,+∞)
解析 (1)函数由y=logau,u=6-ax复合而成,因为a>0,所以u=6-ax是减函数,那么函数y=logau就是增函数,所以a>1,因为[0,2]为定义域的子集,所以当x=2时,u=6-ax取得最小值,所以6-2a>0,解得a<3,所以1
规律方法 1.对数不等式的三种类型及解法
(1)形如logax>logab的不等式,借助函数y=logax的单调性求解,如果a的取值不确定,需分a>1与0
(3)形如logax>logbx的不等式,利用换底公式化为同底的对数进行求解或利用图象求解.
2.若a>1,则y=logaf(x)的单调性与y=f(x)的单调性相同,若0
题型三 对数型函数性质的综合问题
角度1 值域问题
【例3-1】 求下列函数的值域.
(1)y=log2(x2-4x+6);
(2)y=log2(x2-4x-5).
解 (1)令u=x2-4x+6.∵x2-4x+6=(x-2)2+2≥2,
又f(x)=log2u在(0,+∞)上是增函数,∴log2(x2-4x+6)≥log22=1,
∴函数的值域是[1,+∞).
(2)∵x2-4x-5=(x-2)2-9≥-9,∴x2-4x-5能取到所有正实数,
∴函数y=log2(x2-4x-5)的值域是R.
角度2 奇偶性判断
所以f(-x)=-f(x),
角度3 综合应用
解得x>1或x<-1,故此函数的定义域为(-∞,-1)∪(1,+∞).
规律方法 (1)对于y=logaf(x)型函数,在函数定义域中确定t=f(x)的值域,再由y=logat的单调性确定函数的值域.
(2)含对数式的奇偶性判断,一般用f(x)±f(-x)=0来判断,运算相对简单.
【训练3】 已知f(x)=log4(4x-1).
(1)求f(x)的定义域;
(2)讨论f(x)的单调性;
解 (1)由4x-1>0,解得x>0,
因此f(x)的定义域为(0,+∞).
(2)设0
1.由对数函数的图象,反函数概念,研究对数型函数的性质,发展直观想象素养,数学抽象素养及数学运算素养.
2.比较两个对数值的大小及解对数不等式问题,其依据是对数函数的单调性.若对数的底数是字母且范围不明确,一般要分a>1和0
4.y=logaf(x)型函数性质的研究
(1)定义域:由f(x)>0解得x的取值范围,即为函数的定义域.
(2)值域:在函数y=logaf(x)的定义域中确定t=f(x)的值域,再由y=logat的单调性确定函数的值域.
(3)单调性:在定义域内考虑t=f(x)与y=logat的单调性,根据同增异减法则判定(或运用单调性定义判定).
(4)奇偶性:根据奇偶函数的定义判定.
(5)最值:在f(x)>0的条件下,确定t=f(x)的值域,再根据a确定函数y=logat的单调性,最后确定最值.
二、课堂检测
1.函数y=ax与y=-logax(a>0,且a≠1)在同一坐标系中的图象形状可能是( )
解析 函数y=-logax恒过定点(1,0),排除B;当a>1时,y=ax是增函数,y=-logax是减函数,当0
答案 D
3.已知f(x)=|log3x|,若f(a)>f(2),则a的取值范围为________.
解 设t=-x2+2x+1,则t=-(x-1)2+2.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
