苏教版高中数学必修第一册第7章三角函数7.1.2弧度制教学课件(共36张PPT)
文档属性
| 名称 | 苏教版高中数学必修第一册第7章三角函数7.1.2弧度制教学课件(共36张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览











文档简介
(共36张PPT)
7.1角与弧度(第二课时)弧度制
课标要求 素养要求
1.理解角度制与弧度制的概念,能对弧度和角度进行正确的转换.
2.体会引入弧度制的必要性,建立角的集合与实数集的一一对应关系.
3.掌握并能应用弧度制下的弧长公式和扇形面积公式. 1.借助单位圆建立弧度制的概念,体会引入弧度制的必要性,重点提升学生的数学抽象素养.
2.应用弧度制下的弧长公式和扇形面积公式解决相关问题,重点提升数学运算素养.
新知探究
摄氏度与华氏温度
“在一个标准大气压下,把冰水混合物的温度定为零度,把沸水的温度定为100度,它们之间分成100等份,每一等份是摄氏度的一个单位,叫做1摄氏度.”
摄氏度的发明者是安德斯·摄尔修斯(Anders Celsius 1701~1744),其结冰点是0 ℃,沸点为100 ℃.1714年德国人法勒海特(Fahrenheit)以水银为测温介质,制成玻璃水银温度计,选取氯化铵和冰水的混合物的温度为温度计的零度.
人体温度为温度计的100度,把水银温度计从0度到100度按水银的体积膨胀距离分成100份,每一份为1华氏度,记作“1 ?”.按照华氏温标,则水的冰点为32 ?,沸点为212 ?.“华氏温标”是经验温标之一.在美国的日常生活中,多采用这种温标.规定在一大气压下水的冰点为32度,沸点为212度,两个标准点之间分为180等份,每等份代表1度.华氏温度用字母“F”表示.
摄氏温度(℃)和华氏温度(?)之间的换算关系为:
华氏度(?)=32+摄氏度(℃)×1.8,摄氏度(℃)=(华氏度(?)-32)÷1.8.
问题 温度可以用摄氏温度与华氏温度来表示,测量角除了角度外,是否还有其他单位?它是怎样定义的?
提示 弧度,弧长等于半径的弧所对的圆心角即为1弧度的角.
1.度量角的两种单位制
在用弧度制表示角时,单位可以省略
度
弧度
半径长
rad
2.弧度数
(1)正角:正角的弧度数是______.
(2)负角:负角的弧度数是______.
(3)零角:零角的弧度数是____.
(4)如果半径为r的圆的圆心角α所对弧的长为l,那么,角α的弧度数的绝对值是
|α|=______.
正数
负数
0
3.角度制与弧度制的换算
2π rad
360°
π rad
180°
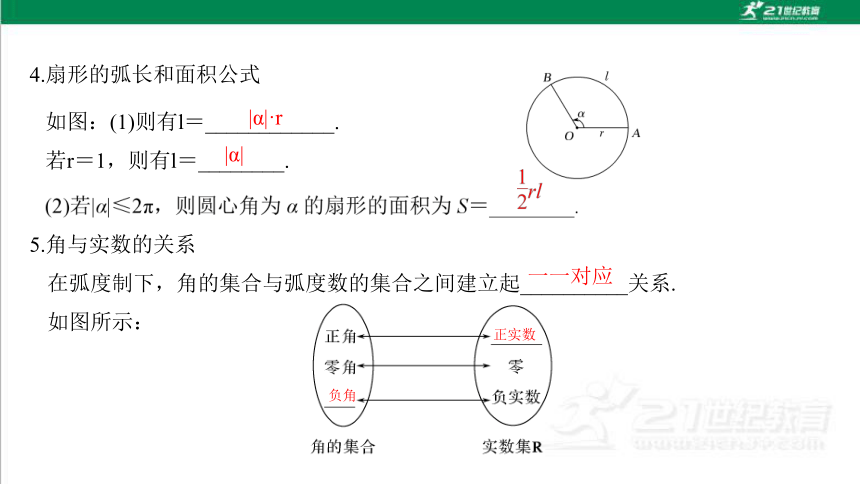
4.扇形的弧长和面积公式
如图:(1)则有l=____________.
若r=1,则有l=________.
5.角与实数的关系
在弧度制下,角的集合与弧度数的集合之间建立起__________关系.
如图所示:
|α|·r
|α|
一一对应
正实数
负角
基础自测
[判断题]
1.1弧度就是1°的圆心角所对的弧.( )
提示 1弧度是长度等于半径的弧所对的圆心角.
2.“1弧度的角”的大小和所在圆的半径大小无关.( )
4.扇形的半径为1 cm,圆心角为30°,则扇形的弧长l=r|α|=1×30=30(cm).( )
提示 扇形的弧长公式l=|α|r,α的单位为弧度.
×
√
√
×
[基础训练]
1.下列命题中的假命题是( )
解析 根据1度、1弧度的定义可知只有D为假命题,故选D.
答案 D
2.将2 340°转化为弧度为________.
答案 13π
4.若θ=-5,则角θ的终边在第________象限.
解析 2π-5与-5的终边相同,
答案 一
[思考]
1.对于角度制和弧度制,在具体的应用中,两者可混用吗?如何书写才是规范的?
2.角α的弧度数与α所在的圆的半径有关吗?
提示 α的弧度数由角α的大小唯一确立,而与其所在圆的大小(半径)无关.
题型一 角度与弧度的互化及应用
【例1】 将下列角度与弧度进行互化:
题型二 用弧度制表示角的集合
【例2】 用弧度表示顶点在原点,始边重合于x轴的非负半轴,终边落在阴影部分内的角的集合(不包括边界,如图).
规律方法 根据已知图形写出区域角的集合的步骤
(1)仔细观察图形.
(2)写出区域边界作为终边时角的表示.
(3)用不等式表示区域范围内的角.
(4)按逆时针方向书写.
【训练2】 已知角α=2 010°.
(1)将α改写成β+2kπ(k∈Z,0≤β<2π)的形式,并指出α是第几象限角;
(2)在区间[-5π,0)上找出与α终边相同的角.
又-5π≤γ<0,
解 如图所示,
根据题意可知,当⊙O1是扇形AOB内切圆时,广场的占地面积最大,
设⊙O1与OA切于C点.连接O1O,O1C.
OO1=OA-O1C=300-O1C,
解得O1C=100 m.
这时⊙O1的面积为π·1002=10 000 π(m2).
规律方法 扇形弧长公式及面积公式的应用类问题的解决方法
首先,将角度转化为弧度表示,弧度制的引入使相关的弧长公式、扇形面积公式均得到了简化,所以解决这类问题时通常采用弧度制.一般地,在几何图形中研究的角,其范围是(0,2π),其次,利用α,l,R,S四个量“知二求二”代入公式.在求解的过程中要注意:
(1)看清角的度量制,选用相应的公式;
(2)扇形的周长等于弧长加两个半径长,对于扇形周长或面积的最值问题,通常转化为某个函数的最值问题.
∴OD=OA+AD=100+20=120,
一、课堂小结
1.通过本节课的学习,重点提升学生的数学抽象、数学运算素养.
2.本节课主要讲述角度制与弧度制的互化和利用弧长公式、面积公式解决有关计算问题.
二、课堂检测
1.下列各命题中,真命题是( )
A.1弧度就是1°的圆心角所对的弧
B.1弧度是长度等于半径的弧
C.1弧度是1°的弧与1°的角之和
D.1弧度是长度等于半径的弧所对的圆心角
解析 根据弧度制和角度制的规定可知A,B,C均错误,D正确.
答案 D
2.将-1 485°化成α+2kπ(0≤α<2π,k∈Z)的形式是( )
答案 D
4.中国扇文化有着深厚的文化底蕴,文人雅士喜在扇面上写字作画.如图是书画家唐寅(1 470—1 523)的一幅书法扇面,其尺寸如图所示,则该扇面的面积为________cm2.
解析 如图,设∠AOB=θ,OA=OB=r,
答案 704
5.已知一个扇形的周长为a,求当扇形的圆心角多大时,扇形的面积最大,并求这个最大值.
解 设扇形的弧长为l,半径为r,圆心角为α,面积为S.由已知,2r+l=a,即l=a-2r.
∵r>0,l=a-2r>0,
7.1角与弧度(第二课时)弧度制
课标要求 素养要求
1.理解角度制与弧度制的概念,能对弧度和角度进行正确的转换.
2.体会引入弧度制的必要性,建立角的集合与实数集的一一对应关系.
3.掌握并能应用弧度制下的弧长公式和扇形面积公式. 1.借助单位圆建立弧度制的概念,体会引入弧度制的必要性,重点提升学生的数学抽象素养.
2.应用弧度制下的弧长公式和扇形面积公式解决相关问题,重点提升数学运算素养.
新知探究
摄氏度与华氏温度
“在一个标准大气压下,把冰水混合物的温度定为零度,把沸水的温度定为100度,它们之间分成100等份,每一等份是摄氏度的一个单位,叫做1摄氏度.”
摄氏度的发明者是安德斯·摄尔修斯(Anders Celsius 1701~1744),其结冰点是0 ℃,沸点为100 ℃.1714年德国人法勒海特(Fahrenheit)以水银为测温介质,制成玻璃水银温度计,选取氯化铵和冰水的混合物的温度为温度计的零度.
人体温度为温度计的100度,把水银温度计从0度到100度按水银的体积膨胀距离分成100份,每一份为1华氏度,记作“1 ?”.按照华氏温标,则水的冰点为32 ?,沸点为212 ?.“华氏温标”是经验温标之一.在美国的日常生活中,多采用这种温标.规定在一大气压下水的冰点为32度,沸点为212度,两个标准点之间分为180等份,每等份代表1度.华氏温度用字母“F”表示.
摄氏温度(℃)和华氏温度(?)之间的换算关系为:
华氏度(?)=32+摄氏度(℃)×1.8,摄氏度(℃)=(华氏度(?)-32)÷1.8.
问题 温度可以用摄氏温度与华氏温度来表示,测量角除了角度外,是否还有其他单位?它是怎样定义的?
提示 弧度,弧长等于半径的弧所对的圆心角即为1弧度的角.
1.度量角的两种单位制
在用弧度制表示角时,单位可以省略
度
弧度
半径长
rad
2.弧度数
(1)正角:正角的弧度数是______.
(2)负角:负角的弧度数是______.
(3)零角:零角的弧度数是____.
(4)如果半径为r的圆的圆心角α所对弧的长为l,那么,角α的弧度数的绝对值是
|α|=______.
正数
负数
0
3.角度制与弧度制的换算
2π rad
360°
π rad
180°
4.扇形的弧长和面积公式
如图:(1)则有l=____________.
若r=1,则有l=________.
5.角与实数的关系
在弧度制下,角的集合与弧度数的集合之间建立起__________关系.
如图所示:
|α|·r
|α|
一一对应
正实数
负角
基础自测
[判断题]
1.1弧度就是1°的圆心角所对的弧.( )
提示 1弧度是长度等于半径的弧所对的圆心角.
2.“1弧度的角”的大小和所在圆的半径大小无关.( )
4.扇形的半径为1 cm,圆心角为30°,则扇形的弧长l=r|α|=1×30=30(cm).( )
提示 扇形的弧长公式l=|α|r,α的单位为弧度.
×
√
√
×
[基础训练]
1.下列命题中的假命题是( )
解析 根据1度、1弧度的定义可知只有D为假命题,故选D.
答案 D
2.将2 340°转化为弧度为________.
答案 13π
4.若θ=-5,则角θ的终边在第________象限.
解析 2π-5与-5的终边相同,
答案 一
[思考]
1.对于角度制和弧度制,在具体的应用中,两者可混用吗?如何书写才是规范的?
2.角α的弧度数与α所在的圆的半径有关吗?
提示 α的弧度数由角α的大小唯一确立,而与其所在圆的大小(半径)无关.
题型一 角度与弧度的互化及应用
【例1】 将下列角度与弧度进行互化:
题型二 用弧度制表示角的集合
【例2】 用弧度表示顶点在原点,始边重合于x轴的非负半轴,终边落在阴影部分内的角的集合(不包括边界,如图).
规律方法 根据已知图形写出区域角的集合的步骤
(1)仔细观察图形.
(2)写出区域边界作为终边时角的表示.
(3)用不等式表示区域范围内的角.
(4)按逆时针方向书写.
【训练2】 已知角α=2 010°.
(1)将α改写成β+2kπ(k∈Z,0≤β<2π)的形式,并指出α是第几象限角;
(2)在区间[-5π,0)上找出与α终边相同的角.
又-5π≤γ<0,
解 如图所示,
根据题意可知,当⊙O1是扇形AOB内切圆时,广场的占地面积最大,
设⊙O1与OA切于C点.连接O1O,O1C.
OO1=OA-O1C=300-O1C,
解得O1C=100 m.
这时⊙O1的面积为π·1002=10 000 π(m2).
规律方法 扇形弧长公式及面积公式的应用类问题的解决方法
首先,将角度转化为弧度表示,弧度制的引入使相关的弧长公式、扇形面积公式均得到了简化,所以解决这类问题时通常采用弧度制.一般地,在几何图形中研究的角,其范围是(0,2π),其次,利用α,l,R,S四个量“知二求二”代入公式.在求解的过程中要注意:
(1)看清角的度量制,选用相应的公式;
(2)扇形的周长等于弧长加两个半径长,对于扇形周长或面积的最值问题,通常转化为某个函数的最值问题.
∴OD=OA+AD=100+20=120,
一、课堂小结
1.通过本节课的学习,重点提升学生的数学抽象、数学运算素养.
2.本节课主要讲述角度制与弧度制的互化和利用弧长公式、面积公式解决有关计算问题.
二、课堂检测
1.下列各命题中,真命题是( )
A.1弧度就是1°的圆心角所对的弧
B.1弧度是长度等于半径的弧
C.1弧度是1°的弧与1°的角之和
D.1弧度是长度等于半径的弧所对的圆心角
解析 根据弧度制和角度制的规定可知A,B,C均错误,D正确.
答案 D
2.将-1 485°化成α+2kπ(0≤α<2π,k∈Z)的形式是( )
答案 D
4.中国扇文化有着深厚的文化底蕴,文人雅士喜在扇面上写字作画.如图是书画家唐寅(1 470—1 523)的一幅书法扇面,其尺寸如图所示,则该扇面的面积为________cm2.
解析 如图,设∠AOB=θ,OA=OB=r,
答案 704
5.已知一个扇形的周长为a,求当扇形的圆心角多大时,扇形的面积最大,并求这个最大值.
解 设扇形的弧长为l,半径为r,圆心角为α,面积为S.由已知,2r+l=a,即l=a-2r.
∵r>0,l=a-2r>0,
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
