苏教版高中数学必修第一册第7章三角函数7.2.3三角函数的诱导公式(第二课时诱导公式五、六)教学课件(共31张PPT)
文档属性
| 名称 | 苏教版高中数学必修第一册第7章三角函数7.2.3三角函数的诱导公式(第二课时诱导公式五、六)教学课件(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
7.2.3 三角函数的诱导公式(第二课时)诱导公式五、六
课标要求 素养要求
1.在诱导公式一~四的基础上,掌握诱导公式五~六的推导.
2.能够利用诱导公式解决简单的求值、化简与证明问题. 通过诱导公式的推导及应用,逐步培养学生的数学抽象、逻辑推理和数学运算素养.
新知探究
同学们听了老师的记忆口诀后,更是摸不着头脑,老师随后做了解释,同学们脑洞大开,都拍手叫绝.
问题 (1)六组诱导公式左边的角能统一写成什么形式?
(2)你能举例说明“奇变偶不变,符号看象限”的含义吗?
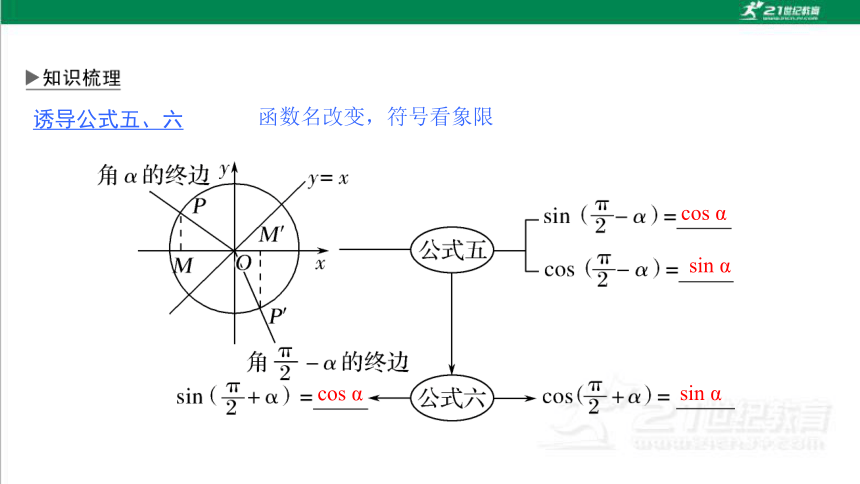
诱导公式五、六
函数名改变,符号看象限
cos α
sin α
cos α
sin α
基础自测
[判断题]
×
×
3.若cos 10°=a,则sin 100°=a.( )
√
√
[训练题]
1.已知sin 25.3°=a,则cos 64.7°=________.
解析 cos 64.7°=cos (90°-25.3°)=sin 25.3°=a.
答案 a
3.cos21°+cos22°+cos23°+…+cos289°=________.
答案 44.5
[思考]
题型一 利用诱导公式求值
∴原等式成立.
规律方法 利用诱导公式证明等式问题,关键在于公式的灵活应用,其证明的常用方法有:
(1)从一边开始,使得它等于另一边,一般由繁到简.
(2)左右归一法:即证明左右两边都等于同一个式子.
(3)针对题设与结论间的差异,有针对性地进行变形,以消除差异.
∴左边=右边,故原等式成立.
题型三 诱导公式的综合应用
一、课堂小结
二、课堂检测
答案 B
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案 B
7.2.3 三角函数的诱导公式(第二课时)诱导公式五、六
课标要求 素养要求
1.在诱导公式一~四的基础上,掌握诱导公式五~六的推导.
2.能够利用诱导公式解决简单的求值、化简与证明问题. 通过诱导公式的推导及应用,逐步培养学生的数学抽象、逻辑推理和数学运算素养.
新知探究
同学们听了老师的记忆口诀后,更是摸不着头脑,老师随后做了解释,同学们脑洞大开,都拍手叫绝.
问题 (1)六组诱导公式左边的角能统一写成什么形式?
(2)你能举例说明“奇变偶不变,符号看象限”的含义吗?
诱导公式五、六
函数名改变,符号看象限
cos α
sin α
cos α
sin α
基础自测
[判断题]
×
×
3.若cos 10°=a,则sin 100°=a.( )
√
√
[训练题]
1.已知sin 25.3°=a,则cos 64.7°=________.
解析 cos 64.7°=cos (90°-25.3°)=sin 25.3°=a.
答案 a
3.cos21°+cos22°+cos23°+…+cos289°=________.
答案 44.5
[思考]
题型一 利用诱导公式求值
∴原等式成立.
规律方法 利用诱导公式证明等式问题,关键在于公式的灵活应用,其证明的常用方法有:
(1)从一边开始,使得它等于另一边,一般由繁到简.
(2)左右归一法:即证明左右两边都等于同一个式子.
(3)针对题设与结论间的差异,有针对性地进行变形,以消除差异.
∴左边=右边,故原等式成立.
题型三 诱导公式的综合应用
一、课堂小结
二、课堂检测
答案 B
A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案 B
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
