苏教版高中数学必修第一册第7章三角函数7.3.2三角函数的图像与性质(第二课时正、余弦函数的图象与性质(二))教学课件(共31张PPT)
文档属性
| 名称 | 苏教版高中数学必修第一册第7章三角函数7.3.2三角函数的图像与性质(第二课时正、余弦函数的图象与性质(二))教学课件(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 20:20:03 | ||
图片预览











文档简介
(共31张PPT)
7.3.2三角函数的图像与性质(第二课时)正、余弦函数的图象与性质(二)
课标要求 素养要求
1.掌握y=sin x,y=cos x的最大值与最小值,并会求简单三角函数的值域和最值.
2.掌握y=sin x,y=cos x的单调性,并能利用单调性比较大小.
3.会求函数y=Asin(ωx+φ)及y=Acos(ωx+φ)的单调区间. 借助y=sin x与y=cos x的图象,理清单调区间和取得最值的条件,构建直观模型,重点提升学生的直观想象、数学抽象、逻辑推理、数学运算素养.
新知探究
过山车是一项富有刺激性的娱乐工具.那种风驰电掣、有惊无险的快感令不少人着迷.过山车的运动包含了许多物理学原理,人们在设计过山车时巧妙地运用了这些原理.如果能亲身体验一下由能量守恒、加速度和力交织在一起产生的效果,那感觉真是妙不可言.一个基本的过山车构造中,包含了爬升、滑落、倒转(儿童过山车没有倒转),几个循环路径.
问题 (1)函数y=sin x与y=cos x也像过山车一样“爬升”,“滑落”,这是y=sin x,y=cos x的哪些性质?
(2)过山车爬升到最高点,然后滑落到最低点,然后再爬升,对应y=sin x,y=cos x的哪些性质?y=sin x,y=cos x在什么位置取得最大(小)值?
提示 (1)单调性. (2)最值,波峰和波谷.
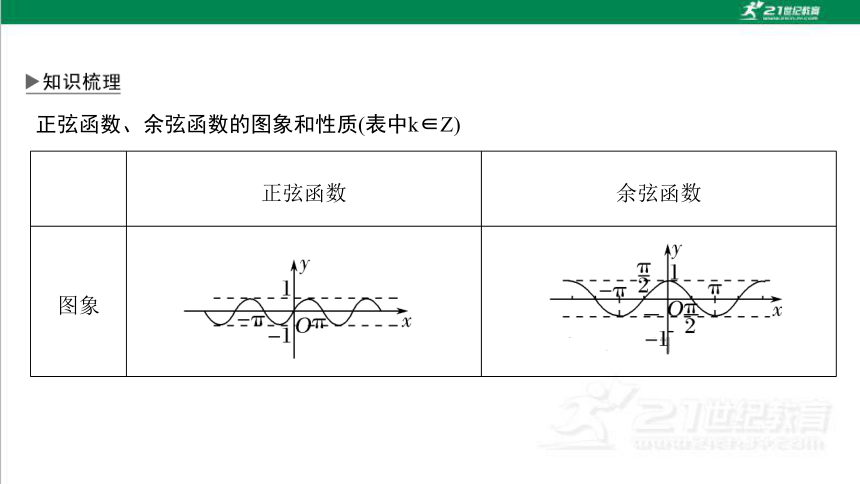
正弦函数、余弦函数的图象和性质(表中k∈Z)
正弦函数 余弦函数
图象
[-1,1]
[-1,1]
[-π+2kπ,2kπ]
[2kπ,π+2kπ]
2kπ
π+2kπ
基础自测
[判断题]
1.正弦函数、余弦函数在定义域内是单调函数.( )
提示 正弦函数、余弦函数在定义域内不单调.
提示 余弦函数最大值为1.
3.余弦函数y=cos x在[0,π]上是减函数.( )
×
×
√
[基础训练]
答案 [1,3]
2.函数y=2-sin x取得最大值时x的值为________.
3.比较sin 250°与sin 260°的大小.
解 ∵sin 250°=sin (180°+70°)=-sin 70°,sin 260°=sin (180°+80°)=-sin 80°,而sin 70°-sin 80°.∴sin 250°>sin 260°.
[思考]
2.正弦函数y=sin x是奇函数,正弦曲线关于原点对称,即原点是正弦曲线的对称中心.
(1)除原点外,正弦曲线还有其他对称中心吗?如果有,那么对称中心的坐标是多少?
(2)正弦函数是轴对称图形吗?如果是,对称轴的方程是什么?
(3)余弦函数y=cos x呢?有以上的性质吗?
提示 (1)y=sin x还有其他对称中心,它们为点(kπ,0)(k∈Z).
(3)y=cos x既是中心对称图形,又是轴对称图形.
题型一 求正弦、余弦函数的单调区间
要求y=-2sin z的单调递增区间,即求sin z的单调递减区间,
规律方法 用整体替换法求函数y=Asin(ωx+φ)或y=Acos(ωx+φ)的单调区间时,如果式子中x的系数为负数,先利用诱导公式将x的系数变为正数再求其单调区间.求单调区间时,需将最终结果写成区间形式.
题型二 利用正弦、余弦函数的单调性比较大小
【例2】 利用三角函数的单调性,比较下列各组数的大小.
规律方法 用正弦函数或余弦函数的单调性比较大小时,应先将异名化同名,把不在同一单调区间内的角用诱导公式转化到同一单调区间,再利用单调性来比较大小.
【训练2】 比较下列各组数的大小:
题型三 正弦、余弦函数的最值(值域)问题
【例3】 求下列函数的值域:
(2)y=cos2x-4cos x+5,令t=cos x,则-1≤t≤1.
y=t2-4t+5=(t-2)2+1,当t=-1,函数取得最大值10;
t=1时,函数取得最小值2,所以函数的值域为[2,10].
规律方法 求三角函数值域或最值的常用方法
(1)形如y=sin(ωx+φ)的三角函数,令t=ωx+φ,根据题中x的取值范围,求出t的取值范围,再利用三角函数的单调性求出y=sin t的最值(值域).
(2)形如y=asin2x+bsin x+c(a≠0)的三角函数,可先设t=sin x,将函数y=asin2x+bsin x+c(a≠0)化为关于t的二次函数y=at2+bt+c(a≠0),根据二次函数的单调性求值域(最值).
(3)对于形如y=asin x(或y=acos x)的函数的最值还要注意对a的讨论.
解 ∵y=a-bcos x(b>0),
∴y=-4acos bx=-2cos x,
所以函数y=-4acos bx的最大值为2,最小值为-2,最小正周期为2π.
一、课堂小结
3.比较三角函数值的大小,先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较,再利用单调性作出判断.
4.求三角函数值域或最值的常用方法:
将y表示成以sin x(或cos x)为元的一次或二次等复合函数,再利用换元或配方或利用函数的单调性等来确定y的范围.
通过上述问题,不断提高学生的数学运算、逻辑推理的素养.
二、课堂检测
A.[-2,2] B.[0,2]
C.[-2,0] D.[-1,1]
答案 A
2.下列关系式中正确的是( )
A.sin 11°B.sin 168°C.sin 11°D.sin 168°解析 因为sin 168°=sin 12°,cos 10°=sin 80°,由正弦函数的单调性得sin 11°答案 C
7.3.2三角函数的图像与性质(第二课时)正、余弦函数的图象与性质(二)
课标要求 素养要求
1.掌握y=sin x,y=cos x的最大值与最小值,并会求简单三角函数的值域和最值.
2.掌握y=sin x,y=cos x的单调性,并能利用单调性比较大小.
3.会求函数y=Asin(ωx+φ)及y=Acos(ωx+φ)的单调区间. 借助y=sin x与y=cos x的图象,理清单调区间和取得最值的条件,构建直观模型,重点提升学生的直观想象、数学抽象、逻辑推理、数学运算素养.
新知探究
过山车是一项富有刺激性的娱乐工具.那种风驰电掣、有惊无险的快感令不少人着迷.过山车的运动包含了许多物理学原理,人们在设计过山车时巧妙地运用了这些原理.如果能亲身体验一下由能量守恒、加速度和力交织在一起产生的效果,那感觉真是妙不可言.一个基本的过山车构造中,包含了爬升、滑落、倒转(儿童过山车没有倒转),几个循环路径.
问题 (1)函数y=sin x与y=cos x也像过山车一样“爬升”,“滑落”,这是y=sin x,y=cos x的哪些性质?
(2)过山车爬升到最高点,然后滑落到最低点,然后再爬升,对应y=sin x,y=cos x的哪些性质?y=sin x,y=cos x在什么位置取得最大(小)值?
提示 (1)单调性. (2)最值,波峰和波谷.
正弦函数、余弦函数的图象和性质(表中k∈Z)
正弦函数 余弦函数
图象
[-1,1]
[-1,1]
[-π+2kπ,2kπ]
[2kπ,π+2kπ]
2kπ
π+2kπ
基础自测
[判断题]
1.正弦函数、余弦函数在定义域内是单调函数.( )
提示 正弦函数、余弦函数在定义域内不单调.
提示 余弦函数最大值为1.
3.余弦函数y=cos x在[0,π]上是减函数.( )
×
×
√
[基础训练]
答案 [1,3]
2.函数y=2-sin x取得最大值时x的值为________.
3.比较sin 250°与sin 260°的大小.
解 ∵sin 250°=sin (180°+70°)=-sin 70°,sin 260°=sin (180°+80°)=-sin 80°,而sin 70°
[思考]
2.正弦函数y=sin x是奇函数,正弦曲线关于原点对称,即原点是正弦曲线的对称中心.
(1)除原点外,正弦曲线还有其他对称中心吗?如果有,那么对称中心的坐标是多少?
(2)正弦函数是轴对称图形吗?如果是,对称轴的方程是什么?
(3)余弦函数y=cos x呢?有以上的性质吗?
提示 (1)y=sin x还有其他对称中心,它们为点(kπ,0)(k∈Z).
(3)y=cos x既是中心对称图形,又是轴对称图形.
题型一 求正弦、余弦函数的单调区间
要求y=-2sin z的单调递增区间,即求sin z的单调递减区间,
规律方法 用整体替换法求函数y=Asin(ωx+φ)或y=Acos(ωx+φ)的单调区间时,如果式子中x的系数为负数,先利用诱导公式将x的系数变为正数再求其单调区间.求单调区间时,需将最终结果写成区间形式.
题型二 利用正弦、余弦函数的单调性比较大小
【例2】 利用三角函数的单调性,比较下列各组数的大小.
规律方法 用正弦函数或余弦函数的单调性比较大小时,应先将异名化同名,把不在同一单调区间内的角用诱导公式转化到同一单调区间,再利用单调性来比较大小.
【训练2】 比较下列各组数的大小:
题型三 正弦、余弦函数的最值(值域)问题
【例3】 求下列函数的值域:
(2)y=cos2x-4cos x+5,令t=cos x,则-1≤t≤1.
y=t2-4t+5=(t-2)2+1,当t=-1,函数取得最大值10;
t=1时,函数取得最小值2,所以函数的值域为[2,10].
规律方法 求三角函数值域或最值的常用方法
(1)形如y=sin(ωx+φ)的三角函数,令t=ωx+φ,根据题中x的取值范围,求出t的取值范围,再利用三角函数的单调性求出y=sin t的最值(值域).
(2)形如y=asin2x+bsin x+c(a≠0)的三角函数,可先设t=sin x,将函数y=asin2x+bsin x+c(a≠0)化为关于t的二次函数y=at2+bt+c(a≠0),根据二次函数的单调性求值域(最值).
(3)对于形如y=asin x(或y=acos x)的函数的最值还要注意对a的讨论.
解 ∵y=a-bcos x(b>0),
∴y=-4acos bx=-2cos x,
所以函数y=-4acos bx的最大值为2,最小值为-2,最小正周期为2π.
一、课堂小结
3.比较三角函数值的大小,先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较,再利用单调性作出判断.
4.求三角函数值域或最值的常用方法:
将y表示成以sin x(或cos x)为元的一次或二次等复合函数,再利用换元或配方或利用函数的单调性等来确定y的范围.
通过上述问题,不断提高学生的数学运算、逻辑推理的素养.
二、课堂检测
A.[-2,2] B.[0,2]
C.[-2,0] D.[-1,1]
答案 A
2.下列关系式中正确的是( )
A.sin 11°
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
