苏教版高中数学必修第一册第7章三角函数7.4三角函数应用教学课件(共32张PPT)
文档属性
| 名称 | 苏教版高中数学必修第一册第7章三角函数7.4三角函数应用教学课件(共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
7.4 三角函数应用
课标要求 素养要求
1.会用三角函数解决简单的实际问题.
2.体会可以利用三角函数构建刻画事物周期变化的数学模型. 通过实际问题,构建三角函数数学模型,重点提升学生的数学抽象、数学运算和数学建模素养.
新知探究
温州市区著名景点——江心屿,江心屿上面有座寺庙——江心寺,在江心寺中题了一副非常知名的对联.上联是:云朝朝 朝朝朝 朝朝朝散;下联是:潮长长 长长长 长长长消.该对联巧妙地运用了叠字诗展现了瓯江潮水涨落的壮阔画面.下面是瓯江江心屿码头在某年某个季节每天的时间与水深的关系表:
江心屿
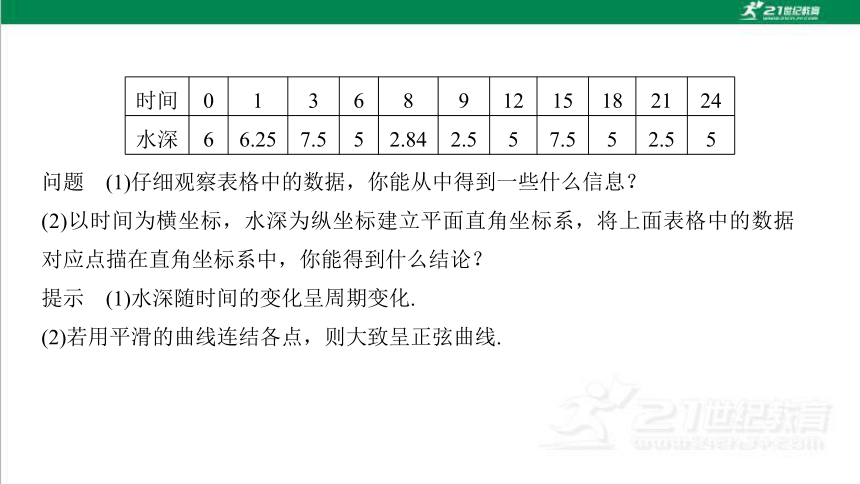
问题 (1)仔细观察表格中的数据,你能从中得到一些什么信息?
(2)以时间为横坐标,水深为纵坐标建立平面直角坐标系,将上面表格中的数据对应点描在直角坐标系中,你能得到什么结论?
提示 (1)水深随时间的变化呈周期变化.
(2)若用平滑的曲线连结各点,则大致呈正弦曲线.
时间 0 1 3 6 8 9 12 15 18 21 24
水深 6 6.25 7.5 5 2.84 2.5 5 7.5 5 2.5 5
简谐运动(单摆、弹簧振子等)是一种周期运动,其运动规律可以用三角函数表达为y=Asin(ωx+φ),其中x表示______,y表示相对于__________的偏离;
①A表示物体运动时离开平衡位置的最大距离,称为______;
时间
平衡位置
振幅
周期
频率
相位
初相
基础自测
[判断题]
1.函数y=Asin(ωx+φ)x∈R的最大值为A.( )
提示 当A>0时,ymax=A;当A<0时,ymax=-A.
2.函数y=Asin(ωx-φ)的初相为φ.( )
提示 初相为-φ.
×
×
√
[基础训练]
答案 2.5
答案 3πx-π
答案 1
1.现实世界中的周期现象可以用哪种数学模型描述?
提示 三角函数模型.
2.在简谐运动中,y=Asin(ωx+φ)的初相,振幅、周期分别为多少?
[思考]
③小球来回摆动一次需要多少时间?
列表:
描点画图:
(2)①小球开始摆动(t=0),离开平衡位置为3 厘米.
②小球摆动时离开平衡位置的最大距离是6 厘米.
③小球来回摆动一次需要1 秒(即周期).
【训练1】 已知电流I与时间t的关系为I=Asin(ωt+φ).
∴ω≥300π>942,又ω∈N+,
故所求最小正整数ω=943.
题型二 三角函数模型在生活中的应用
【例2】 如图,游乐场中的摩天轮匀速旋转,每转一圈需要12分钟,其中心O距离地面40.5米,半径40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时.请解答下列问题.
(1)求出你与地面的距离y与时间t之间的函数解析式;
(2)当你第四次距离地面60.5米时,用了多长时间?
(3)当你登上摩天轮2分钟后,你的朋友也在摩天轮最低处登上摩天轮,问:你的朋友登上摩天轮多长时间后,你和你的朋友与地面的距离之差最大?并求出最大值.
解 (1)可以用余弦型函数来表示该函数解析式,
由已知可设y=40.5-40cos ωt(t≥0),
由周期为12分钟可知,当t=6分钟时到达最高点,
即函数取得最大值,
故80.5=40.5-40cos 6ω,即得cos 6ω=-1,
解得t=4+12k,k∈Z或t=8+12k,k∈Z,
又∵t≥0,故第四次距离地面60.5米时,用了12+8=20(分钟).
(3)与地面的距离之差最大,此时你必须在你的朋友的正上方,或你的朋友在你的正上方,由周期性知,再过2分钟后,你恰好在你的朋友的正上方;再过半个周期时,恰相反,故过(6k+2)(k∈N)分钟后,你和你的朋友与地面的距离之差最大,最大值为40米.
规律方法 解决三角函数的实际应用问题必须按照一般应用题的解题步骤执行:(1)认真审题,理清问题中的已知条件与所求结论.(2)建立三角函数模型,将实际问题数学化.(3)利用三角函数的有关知识解决关于三角函数的问题,求得数学模型的解.(4)根据实际问题的意义,得出实际问题的解.(5)将所得结论返回、转译成实际问题的答案.
一、课堂小结
1.通过本节课的学习,重点提升学生的数学抽象、数学运算、数学建模素养.
2.三角函数模型构建的步骤:
(1)收集数据,观察数据,发现是否具有周期性的重复现象.
(2)制作散点图,选择函数模型进行拟合.
(3)利用三角函数模型解决实际问题.
(4)根据问题的实际意义,对答案的合理性进行检验.
二、课堂检测
答案 A
答案 B
答案 50
5.如图,某动物种群数量1月1日(t=0时)低至700,7月1日高至900,其总量在此两值之间依正弦型曲线变化.
(1)求出种群数量y关于时间t的函数表达式(其中t以年初以来的月为计量单位);
(2)估计当年3月1日动物种群数量.
解 (1)设种群数量y关于t的解析式为y=Asin(ωt+φ)+b(A>0,ω>0),
解得A=100,b=800.
又当t=6时,y=900,
∴sin(π+φ)=1,∴sin φ=-1,
(2)当t=2时,
即当年3月1日动物种群数量约是750.
7.4 三角函数应用
课标要求 素养要求
1.会用三角函数解决简单的实际问题.
2.体会可以利用三角函数构建刻画事物周期变化的数学模型. 通过实际问题,构建三角函数数学模型,重点提升学生的数学抽象、数学运算和数学建模素养.
新知探究
温州市区著名景点——江心屿,江心屿上面有座寺庙——江心寺,在江心寺中题了一副非常知名的对联.上联是:云朝朝 朝朝朝 朝朝朝散;下联是:潮长长 长长长 长长长消.该对联巧妙地运用了叠字诗展现了瓯江潮水涨落的壮阔画面.下面是瓯江江心屿码头在某年某个季节每天的时间与水深的关系表:
江心屿
问题 (1)仔细观察表格中的数据,你能从中得到一些什么信息?
(2)以时间为横坐标,水深为纵坐标建立平面直角坐标系,将上面表格中的数据对应点描在直角坐标系中,你能得到什么结论?
提示 (1)水深随时间的变化呈周期变化.
(2)若用平滑的曲线连结各点,则大致呈正弦曲线.
时间 0 1 3 6 8 9 12 15 18 21 24
水深 6 6.25 7.5 5 2.84 2.5 5 7.5 5 2.5 5
简谐运动(单摆、弹簧振子等)是一种周期运动,其运动规律可以用三角函数表达为y=Asin(ωx+φ),其中x表示______,y表示相对于__________的偏离;
①A表示物体运动时离开平衡位置的最大距离,称为______;
时间
平衡位置
振幅
周期
频率
相位
初相
基础自测
[判断题]
1.函数y=Asin(ωx+φ)x∈R的最大值为A.( )
提示 当A>0时,ymax=A;当A<0时,ymax=-A.
2.函数y=Asin(ωx-φ)的初相为φ.( )
提示 初相为-φ.
×
×
√
[基础训练]
答案 2.5
答案 3πx-π
答案 1
1.现实世界中的周期现象可以用哪种数学模型描述?
提示 三角函数模型.
2.在简谐运动中,y=Asin(ωx+φ)的初相,振幅、周期分别为多少?
[思考]
③小球来回摆动一次需要多少时间?
列表:
描点画图:
(2)①小球开始摆动(t=0),离开平衡位置为3 厘米.
②小球摆动时离开平衡位置的最大距离是6 厘米.
③小球来回摆动一次需要1 秒(即周期).
【训练1】 已知电流I与时间t的关系为I=Asin(ωt+φ).
∴ω≥300π>942,又ω∈N+,
故所求最小正整数ω=943.
题型二 三角函数模型在生活中的应用
【例2】 如图,游乐场中的摩天轮匀速旋转,每转一圈需要12分钟,其中心O距离地面40.5米,半径40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时.请解答下列问题.
(1)求出你与地面的距离y与时间t之间的函数解析式;
(2)当你第四次距离地面60.5米时,用了多长时间?
(3)当你登上摩天轮2分钟后,你的朋友也在摩天轮最低处登上摩天轮,问:你的朋友登上摩天轮多长时间后,你和你的朋友与地面的距离之差最大?并求出最大值.
解 (1)可以用余弦型函数来表示该函数解析式,
由已知可设y=40.5-40cos ωt(t≥0),
由周期为12分钟可知,当t=6分钟时到达最高点,
即函数取得最大值,
故80.5=40.5-40cos 6ω,即得cos 6ω=-1,
解得t=4+12k,k∈Z或t=8+12k,k∈Z,
又∵t≥0,故第四次距离地面60.5米时,用了12+8=20(分钟).
(3)与地面的距离之差最大,此时你必须在你的朋友的正上方,或你的朋友在你的正上方,由周期性知,再过2分钟后,你恰好在你的朋友的正上方;再过半个周期时,恰相反,故过(6k+2)(k∈N)分钟后,你和你的朋友与地面的距离之差最大,最大值为40米.
规律方法 解决三角函数的实际应用问题必须按照一般应用题的解题步骤执行:(1)认真审题,理清问题中的已知条件与所求结论.(2)建立三角函数模型,将实际问题数学化.(3)利用三角函数的有关知识解决关于三角函数的问题,求得数学模型的解.(4)根据实际问题的意义,得出实际问题的解.(5)将所得结论返回、转译成实际问题的答案.
一、课堂小结
1.通过本节课的学习,重点提升学生的数学抽象、数学运算、数学建模素养.
2.三角函数模型构建的步骤:
(1)收集数据,观察数据,发现是否具有周期性的重复现象.
(2)制作散点图,选择函数模型进行拟合.
(3)利用三角函数模型解决实际问题.
(4)根据问题的实际意义,对答案的合理性进行检验.
二、课堂检测
答案 A
答案 B
答案 50
5.如图,某动物种群数量1月1日(t=0时)低至700,7月1日高至900,其总量在此两值之间依正弦型曲线变化.
(1)求出种群数量y关于时间t的函数表达式(其中t以年初以来的月为计量单位);
(2)估计当年3月1日动物种群数量.
解 (1)设种群数量y关于t的解析式为y=Asin(ωt+φ)+b(A>0,ω>0),
解得A=100,b=800.
又当t=6时,y=900,
∴sin(π+φ)=1,∴sin φ=-1,
(2)当t=2时,
即当年3月1日动物种群数量约是750.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
