苏教版高中数学必修第一册第7章三角函数7.3.2三角函数的图像与性质(第三课时正切函数的图象与性质)教学课件(共37张PPT)
文档属性
| 名称 | 苏教版高中数学必修第一册第7章三角函数7.3.2三角函数的图像与性质(第三课时正切函数的图象与性质)教学课件(共37张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 20:25:40 | ||
图片预览











文档简介
(共37张PPT)
7.3.2三角函数的图像与性质(第三课时)正切函数的图象与性质
课标要求 素养要求
1.了解正切函数图象的画法,理解并掌握正切函数的性质.
2.能利用正切函数的图象与性质解决有关问题. 通过利用正切函数的图象,发现数学规律,重点提升学生的数学抽象、逻辑推理素养.
新知探究
学习了y=sin x,y=cos x的图象与性质后,明确了y=sin x,y=cos x的图象是“波浪”型,连续不断的,且都是周期函数,都有最大(小)值.
问题 类比y=sin x,y=cos x的图象与性质.
(1)y=tan x是周期函数吗?有最大(小)值吗?
(2)正切函数的图象是连续的吗?
提示 (1)y=tan x是周期函数,且T=π,无最大,最小值.
(2)正切函数的图象在定义域上不是连续的.
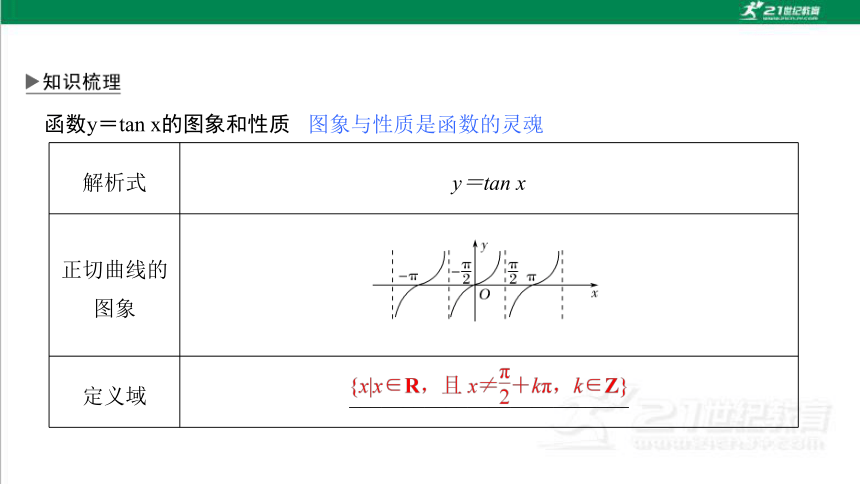
函数y=tan x的图象和性质
图象与性质是函数的灵魂
解析式 y=tan x
正切曲线的图象
定义域 __________________________
R
π
奇函数
基础自测
[判断题]
1.函数y=tan x在其定义域上是增函数.( )
2.函数y=tan 2x的周期为π.( )
×
×
√
√
[基础训练]
1.tan x≥1的解集为( )
答案 D
2.函数y=2tan (-x)是( )
A.奇函数 B.偶函数
C.既是奇函数,又是偶函数 D.非奇非偶函数
解析 y=2tan (-x)=-2tan x,为奇函数.
答案 A
答案 D
[思考]
1.正切曲线是中心对称图形吗?若是,对称中心是什么?是轴对称图形吗?
2.正切函数在其定义域内为增函数是否正确?为什么?
题型一 正切函数的定义域、值域问题
∵二次函数y=u2-2u=(u-1)2-1图象开口向上,对称轴方程为u=1,
∴当u=1时,ymin=-1,
规律方法 (1)求定义域时,要注意正切函数自身的限制条件,另外解不等式时,要充分利用三角函数的图象或三角函数线.
(2)处理正切函数值域时,应注意正切函数自身值域为R,将问题转化为某种函数的值域求解.
又y=tan x的周期为π,
题型二 求正切函数的单调区间
题型三 利用正切函数的单调性比较大小
【例3】 比较大小:
解析 (1)tan 215°=tan(180°+35°)=tan 35°,
∵当0°∴tan 32°答案 (1)< (2)<
规律方法 运用正切函数的单调性比较大小的步骤
(1)运用函数的周期性或诱导公式将角化到同一单调区间内.
(2)运用单调性比较大小关系.
【训练3】 比较下列正切值的大小:
(1)tan 1 320°与tan 70°;
解 (1)tan 1 320°=tan(360°×3+240°)
=tan 240°=tan 60°,
所以tan 60°题型四 正切函数图象、性质的应用
【训练4】 画出f(x)=tan|x|的图象,并根据其图象判断其单调区间、周期性、奇偶性.
根据y=tan x的图象,作出f(x)=tan|x|的图象,如图所示,
一、课堂小结
二、课堂检测
答案 D
答案 C
答案 >
5.求函数y=tan 2x的定义域、值域和周期,并作出它在区间[-π,π]内的图象.
7.3.2三角函数的图像与性质(第三课时)正切函数的图象与性质
课标要求 素养要求
1.了解正切函数图象的画法,理解并掌握正切函数的性质.
2.能利用正切函数的图象与性质解决有关问题. 通过利用正切函数的图象,发现数学规律,重点提升学生的数学抽象、逻辑推理素养.
新知探究
学习了y=sin x,y=cos x的图象与性质后,明确了y=sin x,y=cos x的图象是“波浪”型,连续不断的,且都是周期函数,都有最大(小)值.
问题 类比y=sin x,y=cos x的图象与性质.
(1)y=tan x是周期函数吗?有最大(小)值吗?
(2)正切函数的图象是连续的吗?
提示 (1)y=tan x是周期函数,且T=π,无最大,最小值.
(2)正切函数的图象在定义域上不是连续的.
函数y=tan x的图象和性质
图象与性质是函数的灵魂
解析式 y=tan x
正切曲线的图象
定义域 __________________________
R
π
奇函数
基础自测
[判断题]
1.函数y=tan x在其定义域上是增函数.( )
2.函数y=tan 2x的周期为π.( )
×
×
√
√
[基础训练]
1.tan x≥1的解集为( )
答案 D
2.函数y=2tan (-x)是( )
A.奇函数 B.偶函数
C.既是奇函数,又是偶函数 D.非奇非偶函数
解析 y=2tan (-x)=-2tan x,为奇函数.
答案 A
答案 D
[思考]
1.正切曲线是中心对称图形吗?若是,对称中心是什么?是轴对称图形吗?
2.正切函数在其定义域内为增函数是否正确?为什么?
题型一 正切函数的定义域、值域问题
∵二次函数y=u2-2u=(u-1)2-1图象开口向上,对称轴方程为u=1,
∴当u=1时,ymin=-1,
规律方法 (1)求定义域时,要注意正切函数自身的限制条件,另外解不等式时,要充分利用三角函数的图象或三角函数线.
(2)处理正切函数值域时,应注意正切函数自身值域为R,将问题转化为某种函数的值域求解.
又y=tan x的周期为π,
题型二 求正切函数的单调区间
题型三 利用正切函数的单调性比较大小
【例3】 比较大小:
解析 (1)tan 215°=tan(180°+35°)=tan 35°,
∵当0°
规律方法 运用正切函数的单调性比较大小的步骤
(1)运用函数的周期性或诱导公式将角化到同一单调区间内.
(2)运用单调性比较大小关系.
【训练3】 比较下列正切值的大小:
(1)tan 1 320°与tan 70°;
解 (1)tan 1 320°=tan(360°×3+240°)
=tan 240°=tan 60°,
所以tan 60°
【训练4】 画出f(x)=tan|x|的图象,并根据其图象判断其单调区间、周期性、奇偶性.
根据y=tan x的图象,作出f(x)=tan|x|的图象,如图所示,
一、课堂小结
二、课堂检测
答案 D
答案 C
答案 >
5.求函数y=tan 2x的定义域、值域和周期,并作出它在区间[-π,π]内的图象.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
