苏教版高中数学必修第一册第8章函数应用8.2函数与数学模型(第2课时函数的实际应用)教学课件(共30张PPT)
文档属性
| 名称 | 苏教版高中数学必修第一册第8章函数应用8.2函数与数学模型(第2课时函数的实际应用)教学课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1001.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 20:28:09 | ||
图片预览











文档简介
(共30张PPT)
8.2函数与数学模型(第二课时)
函数的实际应用
课标要求 素养要求
1.会利用已知函数模型解决实际问题.
2.能建立函数模型解决实际问题. 通过本节内容的学习,使学生认识函数模型的作用,提升学生数学建模、数据分析等素养.
新知探究
爱因斯坦说过,复利的威力比原子弹还可怕.若每月坚持投资100元,40年之后将成为百万富翁.也就是说随着变量的增长,指数函数值的增长是非常迅速的,可以根据这一特点来进行资金的管理.例如,按复利计算利率的一种储蓄,本金为a元,每期的利率为r,设本利和为y,存期为x,那么要知道存一定期限之后所得的本利和,就要写出本利和y关于存期x的函数式.假设存入的本金为1 000元,每期的利率为2.25%.
问题 五期后的本利和是多少?
提示 解决这一问题,首先要建立一个指数函数关系式,即y=a(1+r)x,将相应的数据代入该关系式就可得到五年期的本利和.
1.常见的函数模型
常用函数模型 (1)一次函数模型 y=kx+b(k,b为常数,k≠0)
(2)二次函数模型 y=ax2+bx+c(a,b,c为常数,a≠0)
(3)指数函数模型 y=bax+c(a,b,c为常数,b≠0,a>0且a≠1)
(4)对数函数模型 y=mlogax+n(m,a,n为常数,m≠0,a>0且a≠1)
(5)幂函数模型 y=axn+b(a,b为常数,a≠0)
(6)分段函数模型
2.解决实际问题的一般程序:
实际问题→建立数学模型→求解数学模型→解决实际问题
基础自测
[判断题]
1.实际问题中两个变量之间一定有确定的函数关系.( )
提示 两个变量之间可以有关系,但不一定是确定的函数关系.
2.函数模型中,要求的定义域只需使函数式有意义.( )
提示 函数模型中定义域必须满足实际意义.
3.用函数模型预测的结果和实际结果必须相等,否则函数模型就无存在意义了.( )
提示 拟合函数预测的结果近似的符合实际结果即可.
4.利用函数模型求实际应用问题的最值时,要特别注意取得最值时的自变量与实际意义是否相符.( )
×
×
×
√
[基础训练]
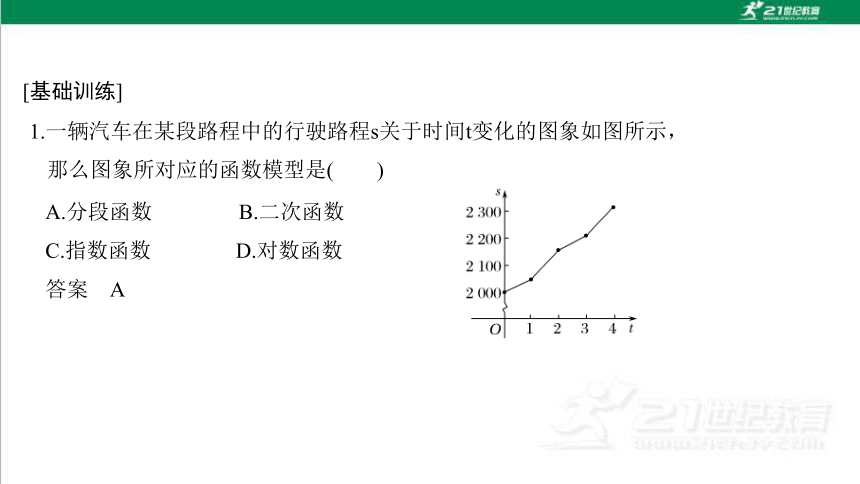
1.一辆汽车在某段路程中的行驶路程s关于时间t变化的图象如图所示,那么图象所对应的函数模型是( )
A.分段函数 B.二次函数
C.指数函数 D.对数函数
答案 A
2.若镭经过100年后剩留原来质量的95.76%,设质量为1的镭经过x年后剩留量为y,则x,y的函数关系是( )
答案 A
3.2014年我国人口总数约为14亿,如果人口的自然年增长率控制在1.25%,则预计________年我国人口将首次超过20亿(lg 2≈0.301 0,lg 3≈0.477 1,lg 7≈0.845 1).
答案 2043
[思考]
在幂函数模型的解析式中,n的正负如何影响函数的单调性?
提示 当x>0,n>0时,函数的图象在第一象限内是上升的,在(0,+∞)上为增函数;当x>0,n<0时,函数的图象在第一象限内是下降的,在(0,+∞)上为减函数.
(1)将利润表示为月产量的函数(用f(x)表示);
(2)当月产量为何值时,车间所获利润最大?最大利润为多少元?(总收入=总成本+利润)
解 (1)设每月产量为x台,则总成本为t=10 000+100x.又f(x)=H(x)-t,
(2)当0≤x≤200时,f(x)=-(x-150)2+12 500,
所以当x=150时,有最大值12 500;
当x>200时,f(x)=30 000-100x是减函数,
f(x)<30 000-100×200<12 500.
所以当x=150时,f(x)取最大值,最大值为12 500.
所以每月生产150台仪器时,利润最大,最大利润为12 500元.
规律方法 1.利用二次函数求最值的方法及注意点
(1)方法:根据实际问题建立函数模型解析式后,可利用配方法、判别式法、换元法及利用函数的单调性等方法求最值,从而解决实际问题中的利润最大、用料最省等最值问题.
(2)注意:取得最值时的自变量与实际意义是否相符.
2.应用分段函数时的三个注意点
(1)分段函数的“段”一定要分得合理,不重不漏.
(2)分段函数的定义域为对应每一段自变量取值范围的并集.
(3)分段函数的值域求法为:逐段求函数值的范围,最后比较再下结论.
【训练1】 在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).某公司每月最多生产100台报警系统装置,生产x台(x∈N*)的收入函数为R(x)=3 000x-20x2(单位:元),其成本函数为C(x)=500x+4 000(单位:元),利润是收入与成本之差.
(1)求利润函数P(x)及边际利润函数MP(x);
(2)利润函数P(x)与边际利润函数MP(x)是否具有相同的最大值?
解 (1)由题意知,x∈[1,100],且x∈N*.
P(x)=R(x)-C(x)=3 000x-20x2-(500x+4 000)=-20x2+2 500x-4 000,
MP(x)=P(x+1)-P(x)
=-20(x+1)2+2 500(x+1)-4 000-(-20x2+2 500x-4 000)=2 480-40x.
因为MP(x)=2 480-40x是减函数,当x=1时,MP(x)的最大值为2 440(元).
因此,利润函数P(x)与边际利润函数MP(x)不具有相同的最大值.
求a和m的值.
(2)为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
(1)已知生活中几种声音的强度如表:
声音来源
声音大小 风吹落叶沙沙声 轻声耳语 很嘈杂的马路
强度I(瓦/平方米) 1×10-11 1×10-10 1×10-3
强弱等级L(分贝) 10 m 90
规律方法 指数型、对数型函数问题的类型及解法
(1)指数函数模型:y=max(a>0且a≠1,m≠0),在实际问题中,有关人口增长、银行利率、细胞分裂等增长率问题都可用指数型函数模型来表示.
(2)对数函数模型:y=mlogax+c(m≠0,a>0且a≠1),对数函数模型一般给出函数关系式,然后利用对数的运算求解.
(3)指数型、对数型函数应用题的解题思路:①依题意找出或建立数学模型,②依实际情况确立解析式中的参数,③依题设数据解决数学问题,④得出结论.
(1)求p%的值;
(2)到今年为止该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
故今后最多还能砍伐15年.
一、课堂小结
1.通过利用已知函数模型解决实际问题,提升数学建模素养;通过建立函数模型解决实际问题,提升数据分析素养.
2.函数模型的应用实例主要包括三个方面:
(1)利用给定的函数模型解决实际问题;
(2)建立确定性的函数模型解决实际问题;
(3)建立拟合函数模型解决实际问题.
3.在引入自变量建立函数解决函数应用题时,一是要注意自变量的取值范围,二是要检验所得结果,必要时运用估算和近似计算,以使结果符合实际问题的要求.
二、课堂检测
1.某种植物生长发育的数量y与时间x的关系如下表:
则下面的函数关系式中拟合效果最好的是( )
A.y=2x-1 B.y=x2-1
C.y=2x-1 D.y=1.5x2-2.5x+2
x 1 2 3 …
y 1 3 8 …
解析 将数值代入各选项中,三个点均与D项吻合,故选D.
答案 D
2.已知国内邮寄1 000 g以内的包裹的邮资标准如下表:
如果某人在西安要邮寄800 g的包裹到距西安1 200 km的某地,那么他应付的邮资是( )
A.5.00元 B.6.00元
C.7.00元 D.8.00元
答案 C
运送距离x(km) 0≤500 500< x≤
1 000 1 0001 500 1 500≤2 000 …
邮资y(元) 5.00 6.00 7.00 8.00 …
3.通常表明地震能量大小的尺度是里氏震级,其计算公式是M=lg A-lg A0,其中,A是被测地震的最大振幅,A0是“标准地震”的振幅,M为震级.则7级地震的最大振幅是5级地震最大振幅的________倍.
答案 100
4.有一位商人从北京向上海的家中打电话,通话m分钟的电话费(单位:元)由函数f(m)=1.06×(0.5[m]+1)决定,其中m>0,[m]是大于或等于m的最小整数,则从北京到上海通话时间为5.5分钟的电话费为________元.
解析 由于f(m)=1.06×(0.5[m]+1),其中m>0,[m]是大于或等于m的最小整数,则当m=5.5时,[m]=6,
即有f(5.5)=1.06×(0.5×6+1)=4.24.
答案 4.24
解 设可获得总利润为R(x)万元,
∵R(x)在[0,210]上是增函数,
∴当x=210时,
∴年产量为210吨时,可获得最大利润1 660万元.
8.2函数与数学模型(第二课时)
函数的实际应用
课标要求 素养要求
1.会利用已知函数模型解决实际问题.
2.能建立函数模型解决实际问题. 通过本节内容的学习,使学生认识函数模型的作用,提升学生数学建模、数据分析等素养.
新知探究
爱因斯坦说过,复利的威力比原子弹还可怕.若每月坚持投资100元,40年之后将成为百万富翁.也就是说随着变量的增长,指数函数值的增长是非常迅速的,可以根据这一特点来进行资金的管理.例如,按复利计算利率的一种储蓄,本金为a元,每期的利率为r,设本利和为y,存期为x,那么要知道存一定期限之后所得的本利和,就要写出本利和y关于存期x的函数式.假设存入的本金为1 000元,每期的利率为2.25%.
问题 五期后的本利和是多少?
提示 解决这一问题,首先要建立一个指数函数关系式,即y=a(1+r)x,将相应的数据代入该关系式就可得到五年期的本利和.
1.常见的函数模型
常用函数模型 (1)一次函数模型 y=kx+b(k,b为常数,k≠0)
(2)二次函数模型 y=ax2+bx+c(a,b,c为常数,a≠0)
(3)指数函数模型 y=bax+c(a,b,c为常数,b≠0,a>0且a≠1)
(4)对数函数模型 y=mlogax+n(m,a,n为常数,m≠0,a>0且a≠1)
(5)幂函数模型 y=axn+b(a,b为常数,a≠0)
(6)分段函数模型
2.解决实际问题的一般程序:
实际问题→建立数学模型→求解数学模型→解决实际问题
基础自测
[判断题]
1.实际问题中两个变量之间一定有确定的函数关系.( )
提示 两个变量之间可以有关系,但不一定是确定的函数关系.
2.函数模型中,要求的定义域只需使函数式有意义.( )
提示 函数模型中定义域必须满足实际意义.
3.用函数模型预测的结果和实际结果必须相等,否则函数模型就无存在意义了.( )
提示 拟合函数预测的结果近似的符合实际结果即可.
4.利用函数模型求实际应用问题的最值时,要特别注意取得最值时的自变量与实际意义是否相符.( )
×
×
×
√
[基础训练]
1.一辆汽车在某段路程中的行驶路程s关于时间t变化的图象如图所示,那么图象所对应的函数模型是( )
A.分段函数 B.二次函数
C.指数函数 D.对数函数
答案 A
2.若镭经过100年后剩留原来质量的95.76%,设质量为1的镭经过x年后剩留量为y,则x,y的函数关系是( )
答案 A
3.2014年我国人口总数约为14亿,如果人口的自然年增长率控制在1.25%,则预计________年我国人口将首次超过20亿(lg 2≈0.301 0,lg 3≈0.477 1,lg 7≈0.845 1).
答案 2043
[思考]
在幂函数模型的解析式中,n的正负如何影响函数的单调性?
提示 当x>0,n>0时,函数的图象在第一象限内是上升的,在(0,+∞)上为增函数;当x>0,n<0时,函数的图象在第一象限内是下降的,在(0,+∞)上为减函数.
(1)将利润表示为月产量的函数(用f(x)表示);
(2)当月产量为何值时,车间所获利润最大?最大利润为多少元?(总收入=总成本+利润)
解 (1)设每月产量为x台,则总成本为t=10 000+100x.又f(x)=H(x)-t,
(2)当0≤x≤200时,f(x)=-(x-150)2+12 500,
所以当x=150时,有最大值12 500;
当x>200时,f(x)=30 000-100x是减函数,
f(x)<30 000-100×200<12 500.
所以当x=150时,f(x)取最大值,最大值为12 500.
所以每月生产150台仪器时,利润最大,最大利润为12 500元.
规律方法 1.利用二次函数求最值的方法及注意点
(1)方法:根据实际问题建立函数模型解析式后,可利用配方法、判别式法、换元法及利用函数的单调性等方法求最值,从而解决实际问题中的利润最大、用料最省等最值问题.
(2)注意:取得最值时的自变量与实际意义是否相符.
2.应用分段函数时的三个注意点
(1)分段函数的“段”一定要分得合理,不重不漏.
(2)分段函数的定义域为对应每一段自变量取值范围的并集.
(3)分段函数的值域求法为:逐段求函数值的范围,最后比较再下结论.
【训练1】 在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).某公司每月最多生产100台报警系统装置,生产x台(x∈N*)的收入函数为R(x)=3 000x-20x2(单位:元),其成本函数为C(x)=500x+4 000(单位:元),利润是收入与成本之差.
(1)求利润函数P(x)及边际利润函数MP(x);
(2)利润函数P(x)与边际利润函数MP(x)是否具有相同的最大值?
解 (1)由题意知,x∈[1,100],且x∈N*.
P(x)=R(x)-C(x)=3 000x-20x2-(500x+4 000)=-20x2+2 500x-4 000,
MP(x)=P(x+1)-P(x)
=-20(x+1)2+2 500(x+1)-4 000-(-20x2+2 500x-4 000)=2 480-40x.
因为MP(x)=2 480-40x是减函数,当x=1时,MP(x)的最大值为2 440(元).
因此,利润函数P(x)与边际利润函数MP(x)不具有相同的最大值.
求a和m的值.
(2)为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
(1)已知生活中几种声音的强度如表:
声音来源
声音大小 风吹落叶沙沙声 轻声耳语 很嘈杂的马路
强度I(瓦/平方米) 1×10-11 1×10-10 1×10-3
强弱等级L(分贝) 10 m 90
规律方法 指数型、对数型函数问题的类型及解法
(1)指数函数模型:y=max(a>0且a≠1,m≠0),在实际问题中,有关人口增长、银行利率、细胞分裂等增长率问题都可用指数型函数模型来表示.
(2)对数函数模型:y=mlogax+c(m≠0,a>0且a≠1),对数函数模型一般给出函数关系式,然后利用对数的运算求解.
(3)指数型、对数型函数应用题的解题思路:①依题意找出或建立数学模型,②依实际情况确立解析式中的参数,③依题设数据解决数学问题,④得出结论.
(1)求p%的值;
(2)到今年为止该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
故今后最多还能砍伐15年.
一、课堂小结
1.通过利用已知函数模型解决实际问题,提升数学建模素养;通过建立函数模型解决实际问题,提升数据分析素养.
2.函数模型的应用实例主要包括三个方面:
(1)利用给定的函数模型解决实际问题;
(2)建立确定性的函数模型解决实际问题;
(3)建立拟合函数模型解决实际问题.
3.在引入自变量建立函数解决函数应用题时,一是要注意自变量的取值范围,二是要检验所得结果,必要时运用估算和近似计算,以使结果符合实际问题的要求.
二、课堂检测
1.某种植物生长发育的数量y与时间x的关系如下表:
则下面的函数关系式中拟合效果最好的是( )
A.y=2x-1 B.y=x2-1
C.y=2x-1 D.y=1.5x2-2.5x+2
x 1 2 3 …
y 1 3 8 …
解析 将数值代入各选项中,三个点均与D项吻合,故选D.
答案 D
2.已知国内邮寄1 000 g以内的包裹的邮资标准如下表:
如果某人在西安要邮寄800 g的包裹到距西安1 200 km的某地,那么他应付的邮资是( )
A.5.00元 B.6.00元
C.7.00元 D.8.00元
答案 C
运送距离x(km) 0
1 000 1 000
邮资y(元) 5.00 6.00 7.00 8.00 …
3.通常表明地震能量大小的尺度是里氏震级,其计算公式是M=lg A-lg A0,其中,A是被测地震的最大振幅,A0是“标准地震”的振幅,M为震级.则7级地震的最大振幅是5级地震最大振幅的________倍.
答案 100
4.有一位商人从北京向上海的家中打电话,通话m分钟的电话费(单位:元)由函数f(m)=1.06×(0.5[m]+1)决定,其中m>0,[m]是大于或等于m的最小整数,则从北京到上海通话时间为5.5分钟的电话费为________元.
解析 由于f(m)=1.06×(0.5[m]+1),其中m>0,[m]是大于或等于m的最小整数,则当m=5.5时,[m]=6,
即有f(5.5)=1.06×(0.5×6+1)=4.24.
答案 4.24
解 设可获得总利润为R(x)万元,
∵R(x)在[0,210]上是增函数,
∴当x=210时,
∴年产量为210吨时,可获得最大利润1 660万元.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
