人教新课标A数学必修1 第三章函数的应用质量检测
文档属性
| 名称 | 人教新课标A数学必修1 第三章函数的应用质量检测 |

|
|
| 格式 | zip | ||
| 文件大小 | 404.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-29 00:00:00 | ||
图片预览




文档简介
第三章函数的应用质量检测
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.21世纪教育网版权所有
1.函数的零点所在的大致区间是 ( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
2.若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:21·cn·jy·com
那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为 ( )
A、1.2 B、1.3 C、1.4 D、1.5
3.函数的零点个数是( )
A.1 B.2 C. 3 D.42·1·c·n·j·y
4.二次方程,有一个根比大,另一个根比小,则的取值范围是( )
A. B.
C. D.
5.已知函数,,若,则( )
A.1 B.2 C.3 D.-1
6.已知函数,把函数的零点从小到大的顺序排成一列,依次为,则与大小关系为( )
A. B. C. D.无法确定
7.若函数恰有三个不同的零点,则实数的最大值是( )
A.1 B.1.5 C.2 D.2.5
8.已知两地相距千米,某人开汽车以千米/小时的速度从地到达地,在地停留小时后再以千米/小时的速度返回地,把汽车离开地的距离表示为时间(小时)的函数表达式( )www.21-cn-jy.com
A. B.
C. D.
9.是定义在上的奇函数,且当时,,则函数的零点的个数是( )
A. B. C. D.【来源:21·世纪·教育·网】
10.襄荆高速公路连接襄阳、荆门、荆州三市,全长约188公里,是湖北省大三角经济主骨架的干线公路之一.若某汽车从进入该高速公路后以不低于60千米/时且不高于120千米/时的速度匀速行驶,已知该汽车每小时的运输成本由固定部分和可变部分组成,固定部分为200元,可变部分与速度v(千米/时)的平方成正比(比例系数记为k).当汽车以最快速度行驶时,每小时的运输成本为488元.若使汽车的全程运输成本最低,其速度为
A.80 km /小时 B.90 km /小时 C.100 km /小时 D.110 km /小时
11.如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为,运动的距离为.下面表示与的函数关系式的图象大致是( )21·世纪*教育网
12.设函数,若对任意,都存在,使,则实数的取值范围为( )
A. B. C. D.
二、填空题(每题4分,满分16分,将答案填在答题纸上)
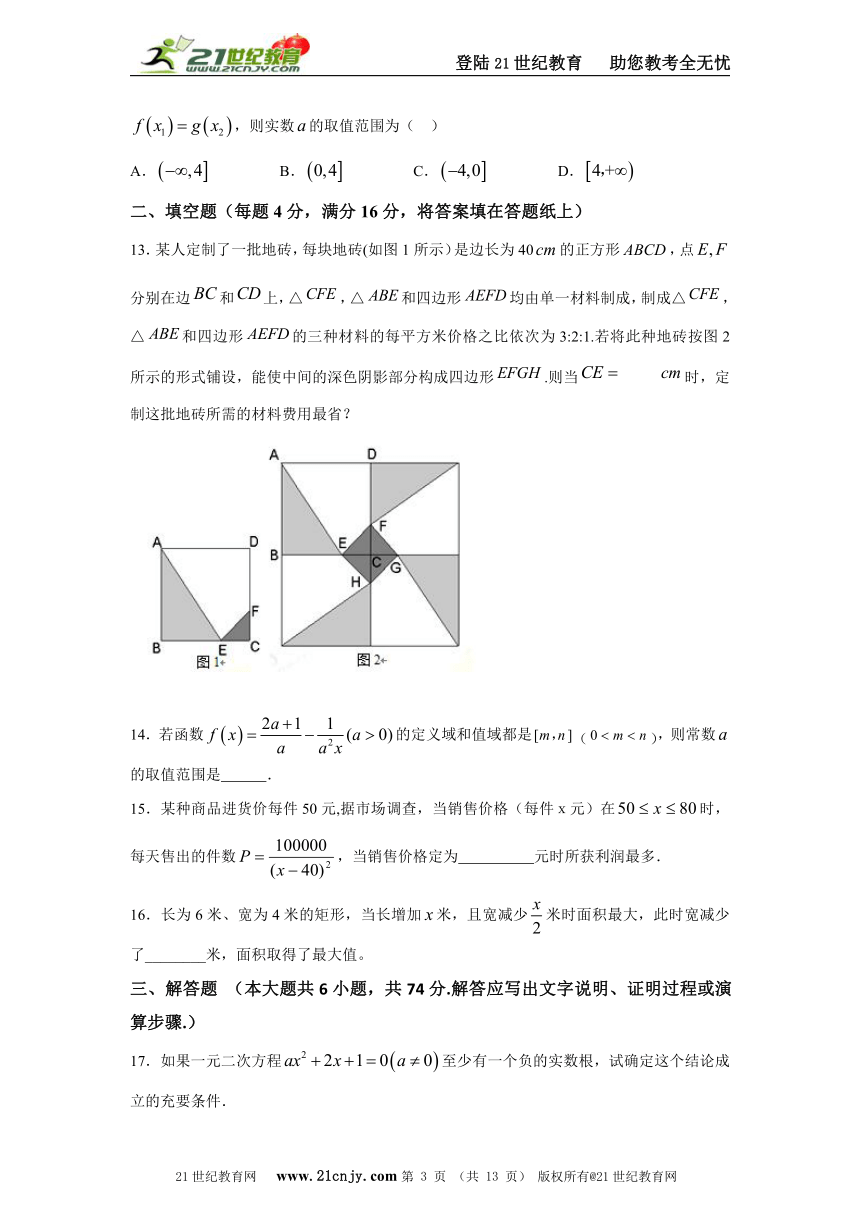
13.某人定制了一批地砖,每块地砖(如图1所示)是边长为40的正方形,点分别在边和上,△,△和四边形均由单一材料制成,制成△,△和四边形的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形.则当 时,定制这批地砖所需的材料费用最省?www-2-1-cnjy-com
14.若函数的定义域和值域都是(),则常数的取值范围是 .
15.某种商品进货价每件50元,据市场调查,当销售价格(每件x元)在时,每天售出的件数,当销售价格定为 元时所获利润最多.
16.长为6米、宽为4米的矩形,当长增加米,且宽减少米时面积最大,此时宽减少了________米,面积取得了最大值。2-1-c-n-j-y
三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
17.如果一元二次方程至少有一个负的实数根,试确定这个结论成立的充要条件.
18.双流中学食堂旁边有一块矩形空地,学校想要在这块空地上修建一个内接四边形花坛(如下图所示),该花坛的四个顶点分别落在矩形的四条边上,已知,,且,设,花坛的面积记为. 21*cnjy*com
(1)求的解析式,并指出这个函数的定义域;
(2)当为何值时,花坛面积最大?并求出最大面积.
19.已知函数.
(1)求的单调区间;
(2)若方程有四个不等实根,求实数的取值范围.
20.已知函数.
(I)若,试比较与的大小;
(Ⅱ)若函数,且在区间上没有零点,求实数m的取值范围.
21.已知函数,函数
(1)当时,求时的最大值;
(2)若在恒成立,求的取值范围;
(3)当时,函数在有两个不同的零点,求的取值范围.
22.已知函数且.
(Ⅰ) 若1是关于x的方程的一个解,求t的值;
(Ⅱ) 当且时,解不等式;
(Ⅲ)若函数在区间(-1,2]上有零点,求t的取值范围.
第三章函数的应用质量检测
参考答案及解析
1.B【解析】∵,而,
∴函数的零点所在区间是 (1,2),故选B.
2.C【解析】在区间上有零点,即方程x3+x2-2x-2=0的根在上,所以近似根为1.4
3.D【解析】由题,求零点得:,得: ,零点为:,有4个.
4.C【解析】设,因为方程有一个根比大,另一个根比小,所以整理可得,解得,故选C.
5.A【解析】由题意可得:.
6.B【解析】因为函数,所以
函数的零点即是的根,所以,故选B.
7.C【解析】由题意得,函数恰有三个不同的零点,则函数在区间上有一个零点,在区间上有两个零点,所以,解得,所以实数的最大值是,故选C.21教育网
8.D【解析】在从地到达地的过程中,时间满足,距离与时间的关系为;在地停留小时,则,而不变;返回地的过程中,时间满足,距离与时间的关系为.故选择D.【来源:21cnj*y.co*m】
9.B【解析】函数在上为单调递增函数,且当时,,即存在使得,结合函数的单调性可知函数在有且仅有一个零点;因为函数为奇函数,所以在上也只有一个零点,故本题的正确选项为B.【出处:21教育名师】
10.C【解析】每小时的运输成本为,由汽车以最快速度行驶时,每小时的运输成本为488元可求出,全程运输成本为,由基本不等式可知,当且仅当即时取得最小值,答案选C.
11.C【解析】设等腰直角三角形的直角边长为1,当0≤x≤1时,
三角形CEG的面积y=EC?GE=x2为抛物线,
当1<x≤2时,
重合的部分为△FBG,此时EC=x,BE=x-1,BF=1-(x-1)=2-x,对应的面积y=(2-x)2,x>1.故对应的图象为C, 故选:C【版权所有:21教育】
12.A【解析】
设的值域为,由于值域为,要取遍中的每一个数,又,于是,实数满足
13.10【解析】设,则,设△,△和四边形的面积,分别为,地砖的总费用为,则
二次函数开口向上,其对称轴为 ,所以时,即费用最少.
14.【解析】分析可知函数在定义域上单调递增,于是根据题意,从而可知是方程的二不等实根,即,于是,注意到,解得.21教育名师原创作品
15.60【解析】设销售价格每件元,每天获利润元,
则;
问题转化为的最大值即可,
这是一个关于的二次函数,
当,即时,取得最大值.
所以当销售价格每件为60元时所获利润最大.
16.0.5(或米)【解析】由题意有:设面积为,
则
当米时, 则米。故填0.5(或米)。
17.【解析】由题意得 ,一元二次方程有实数根的充要条件是,即,设方程的根是,由,可知,方程有一个负的实数根,即,方程有两个负的实数根,即,综上所述,一元二次方程至少有一个负实数根的充要条件是或.
18.【解析】(1)
则
由,得
(2)由(1)知
综上所述:当时,;
当时,
19. 【解析】(1).
由反比例函数的单调性知:
的单调递减区间是和,单调递增区间是.
(2)①若,则方程,即,由(1)知,仅唯一零点,不合题意;
②若,有四个实根即函数与开口向下的抛物线有四个交点.
当时,单调递减,单调递增,故最多一个交点,
当时,,,仅有一个交点,这与他们有四个交点不符;
③若,由知,是其一根.
当时,有,即.
因为,所以该方程在实数范围有两根,而,
故方程在上仅有一根,
因此在上有两实数根,
即在上有两实数根,等价于有两个不等的负实根,
令,又,故,
此时由韦达定理知有两个不等负根,且均不等于.
综上可知的取值范围是.
20.【解析】(I).
当时,,
所以,从而,
即.
所以.
(Ⅱ)由(I)知,在递增,
所以在递增.
∵ 在区间上没有零点,
∴
或,
∴ 或.
21.【解析】(1),在单调递增,
(2)在恒成立,在恒成立
(3)解法一:当时,函数,有两个不同的零点
在有两个不同的解
令作出函数的图象容易得出:
解法二:在有两个不同的解,令
解得:
22.【解析】(Ⅰ)∵若1是关于的方程的解,
,又.
(Ⅱ) 时,,
又,∴解集为:;
(Ⅲ)若,则在上没有零点.下面就时分三种情况讨论:方程在上有重根,则,解得;①
在上只有一个零点,且不是方程的重根,则有,解得,又经检验:时,在上都有零点,.②;在上有两个相异实根,则有:21cnjy.com
或,解得,③;综合①②③可知的取值范围为或.
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.21世纪教育网版权所有
1.函数的零点所在的大致区间是 ( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
2.若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,参考数据如下表:21·cn·jy·com
那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为 ( )
A、1.2 B、1.3 C、1.4 D、1.5
3.函数的零点个数是( )
A.1 B.2 C. 3 D.42·1·c·n·j·y
4.二次方程,有一个根比大,另一个根比小,则的取值范围是( )
A. B.
C. D.
5.已知函数,,若,则( )
A.1 B.2 C.3 D.-1
6.已知函数,把函数的零点从小到大的顺序排成一列,依次为,则与大小关系为( )
A. B. C. D.无法确定
7.若函数恰有三个不同的零点,则实数的最大值是( )
A.1 B.1.5 C.2 D.2.5
8.已知两地相距千米,某人开汽车以千米/小时的速度从地到达地,在地停留小时后再以千米/小时的速度返回地,把汽车离开地的距离表示为时间(小时)的函数表达式( )www.21-cn-jy.com
A. B.
C. D.
9.是定义在上的奇函数,且当时,,则函数的零点的个数是( )
A. B. C. D.【来源:21·世纪·教育·网】
10.襄荆高速公路连接襄阳、荆门、荆州三市,全长约188公里,是湖北省大三角经济主骨架的干线公路之一.若某汽车从进入该高速公路后以不低于60千米/时且不高于120千米/时的速度匀速行驶,已知该汽车每小时的运输成本由固定部分和可变部分组成,固定部分为200元,可变部分与速度v(千米/时)的平方成正比(比例系数记为k).当汽车以最快速度行驶时,每小时的运输成本为488元.若使汽车的全程运输成本最低,其速度为
A.80 km /小时 B.90 km /小时 C.100 km /小时 D.110 km /小时
11.如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为,运动的距离为.下面表示与的函数关系式的图象大致是( )21·世纪*教育网
12.设函数,若对任意,都存在,使,则实数的取值范围为( )
A. B. C. D.
二、填空题(每题4分,满分16分,将答案填在答题纸上)
13.某人定制了一批地砖,每块地砖(如图1所示)是边长为40的正方形,点分别在边和上,△,△和四边形均由单一材料制成,制成△,△和四边形的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形.则当 时,定制这批地砖所需的材料费用最省?www-2-1-cnjy-com
14.若函数的定义域和值域都是(),则常数的取值范围是 .
15.某种商品进货价每件50元,据市场调查,当销售价格(每件x元)在时,每天售出的件数,当销售价格定为 元时所获利润最多.
16.长为6米、宽为4米的矩形,当长增加米,且宽减少米时面积最大,此时宽减少了________米,面积取得了最大值。2-1-c-n-j-y
三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
17.如果一元二次方程至少有一个负的实数根,试确定这个结论成立的充要条件.
18.双流中学食堂旁边有一块矩形空地,学校想要在这块空地上修建一个内接四边形花坛(如下图所示),该花坛的四个顶点分别落在矩形的四条边上,已知,,且,设,花坛的面积记为. 21*cnjy*com
(1)求的解析式,并指出这个函数的定义域;
(2)当为何值时,花坛面积最大?并求出最大面积.
19.已知函数.
(1)求的单调区间;
(2)若方程有四个不等实根,求实数的取值范围.
20.已知函数.
(I)若,试比较与的大小;
(Ⅱ)若函数,且在区间上没有零点,求实数m的取值范围.
21.已知函数,函数
(1)当时,求时的最大值;
(2)若在恒成立,求的取值范围;
(3)当时,函数在有两个不同的零点,求的取值范围.
22.已知函数且.
(Ⅰ) 若1是关于x的方程的一个解,求t的值;
(Ⅱ) 当且时,解不等式;
(Ⅲ)若函数在区间(-1,2]上有零点,求t的取值范围.
第三章函数的应用质量检测
参考答案及解析
1.B【解析】∵,而,
∴函数的零点所在区间是 (1,2),故选B.
2.C【解析】在区间上有零点,即方程x3+x2-2x-2=0的根在上,所以近似根为1.4
3.D【解析】由题,求零点得:,得: ,零点为:,有4个.
4.C【解析】设,因为方程有一个根比大,另一个根比小,所以整理可得,解得,故选C.
5.A【解析】由题意可得:.
6.B【解析】因为函数,所以
函数的零点即是的根,所以,故选B.
7.C【解析】由题意得,函数恰有三个不同的零点,则函数在区间上有一个零点,在区间上有两个零点,所以,解得,所以实数的最大值是,故选C.21教育网
8.D【解析】在从地到达地的过程中,时间满足,距离与时间的关系为;在地停留小时,则,而不变;返回地的过程中,时间满足,距离与时间的关系为.故选择D.【来源:21cnj*y.co*m】
9.B【解析】函数在上为单调递增函数,且当时,,即存在使得,结合函数的单调性可知函数在有且仅有一个零点;因为函数为奇函数,所以在上也只有一个零点,故本题的正确选项为B.【出处:21教育名师】
10.C【解析】每小时的运输成本为,由汽车以最快速度行驶时,每小时的运输成本为488元可求出,全程运输成本为,由基本不等式可知,当且仅当即时取得最小值,答案选C.
11.C【解析】设等腰直角三角形的直角边长为1,当0≤x≤1时,
三角形CEG的面积y=EC?GE=x2为抛物线,
当1<x≤2时,
重合的部分为△FBG,此时EC=x,BE=x-1,BF=1-(x-1)=2-x,对应的面积y=(2-x)2,x>1.故对应的图象为C, 故选:C【版权所有:21教育】
12.A【解析】
设的值域为,由于值域为,要取遍中的每一个数,又,于是,实数满足
13.10【解析】设,则,设△,△和四边形的面积,分别为,地砖的总费用为,则
二次函数开口向上,其对称轴为 ,所以时,即费用最少.
14.【解析】分析可知函数在定义域上单调递增,于是根据题意,从而可知是方程的二不等实根,即,于是,注意到,解得.21教育名师原创作品
15.60【解析】设销售价格每件元,每天获利润元,
则;
问题转化为的最大值即可,
这是一个关于的二次函数,
当,即时,取得最大值.
所以当销售价格每件为60元时所获利润最大.
16.0.5(或米)【解析】由题意有:设面积为,
则
当米时, 则米。故填0.5(或米)。
17.【解析】由题意得 ,一元二次方程有实数根的充要条件是,即,设方程的根是,由,可知,方程有一个负的实数根,即,方程有两个负的实数根,即,综上所述,一元二次方程至少有一个负实数根的充要条件是或.
18.【解析】(1)
则
由,得
(2)由(1)知
综上所述:当时,;
当时,
19. 【解析】(1).
由反比例函数的单调性知:
的单调递减区间是和,单调递增区间是.
(2)①若,则方程,即,由(1)知,仅唯一零点,不合题意;
②若,有四个实根即函数与开口向下的抛物线有四个交点.
当时,单调递减,单调递增,故最多一个交点,
当时,,,仅有一个交点,这与他们有四个交点不符;
③若,由知,是其一根.
当时,有,即.
因为,所以该方程在实数范围有两根,而,
故方程在上仅有一根,
因此在上有两实数根,
即在上有两实数根,等价于有两个不等的负实根,
令,又,故,
此时由韦达定理知有两个不等负根,且均不等于.
综上可知的取值范围是.
20.【解析】(I).
当时,,
所以,从而,
即.
所以.
(Ⅱ)由(I)知,在递增,
所以在递增.
∵ 在区间上没有零点,
∴
或,
∴ 或.
21.【解析】(1),在单调递增,
(2)在恒成立,在恒成立
(3)解法一:当时,函数,有两个不同的零点
在有两个不同的解
令作出函数的图象容易得出:
解法二:在有两个不同的解,令
解得:
22.【解析】(Ⅰ)∵若1是关于的方程的解,
,又.
(Ⅱ) 时,,
又,∴解集为:;
(Ⅲ)若,则在上没有零点.下面就时分三种情况讨论:方程在上有重根,则,解得;①
在上只有一个零点,且不是方程的重根,则有,解得,又经检验:时,在上都有零点,.②;在上有两个相异实根,则有:21cnjy.com
或,解得,③;综合①②③可知的取值范围为或.
