初中数学沪科版九年级下册 24.3 圆周角 教学设计
文档属性
| 名称 | 初中数学沪科版九年级下册 24.3 圆周角 教学设计 | 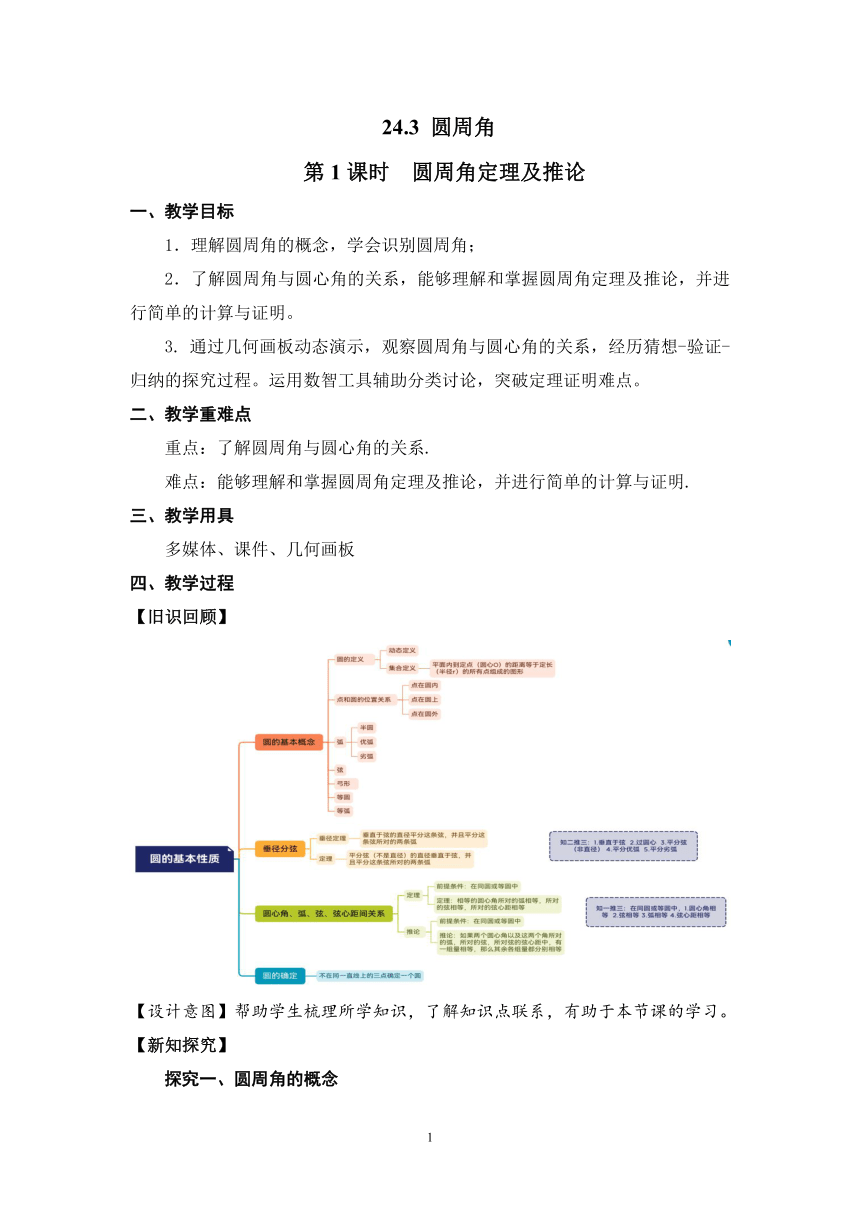 | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 11:51:17 | ||
图片预览



文档简介
24.3 圆周角
第1课时 圆周角定理及推论
一、教学目标
1.理解圆周角的概念,学会识别圆周角;
2.了解圆周角与圆心角的关系,能够理解和掌握圆周角定理及推论,并进行简单的计算与证明。
3. 通过几何画板动态演示,观察圆周角与圆心角的关系,经历猜想-验证-归纳的探究过程。运用数智工具辅助分类讨论,突破定理证明难点。
二、教学重难点
重点:了解圆周角与圆心角的关系.
难点:能够理解和掌握圆周角定理及推论,并进行简单的计算与证明.
三、教学用具
多媒体、课件、几何画板
四、教学过程
【旧识回顾】
【设计意图】帮助学生梳理所学知识,了解知识点联系,有助于本节课的学习。
【新知探究】
探究一、圆周角的概念
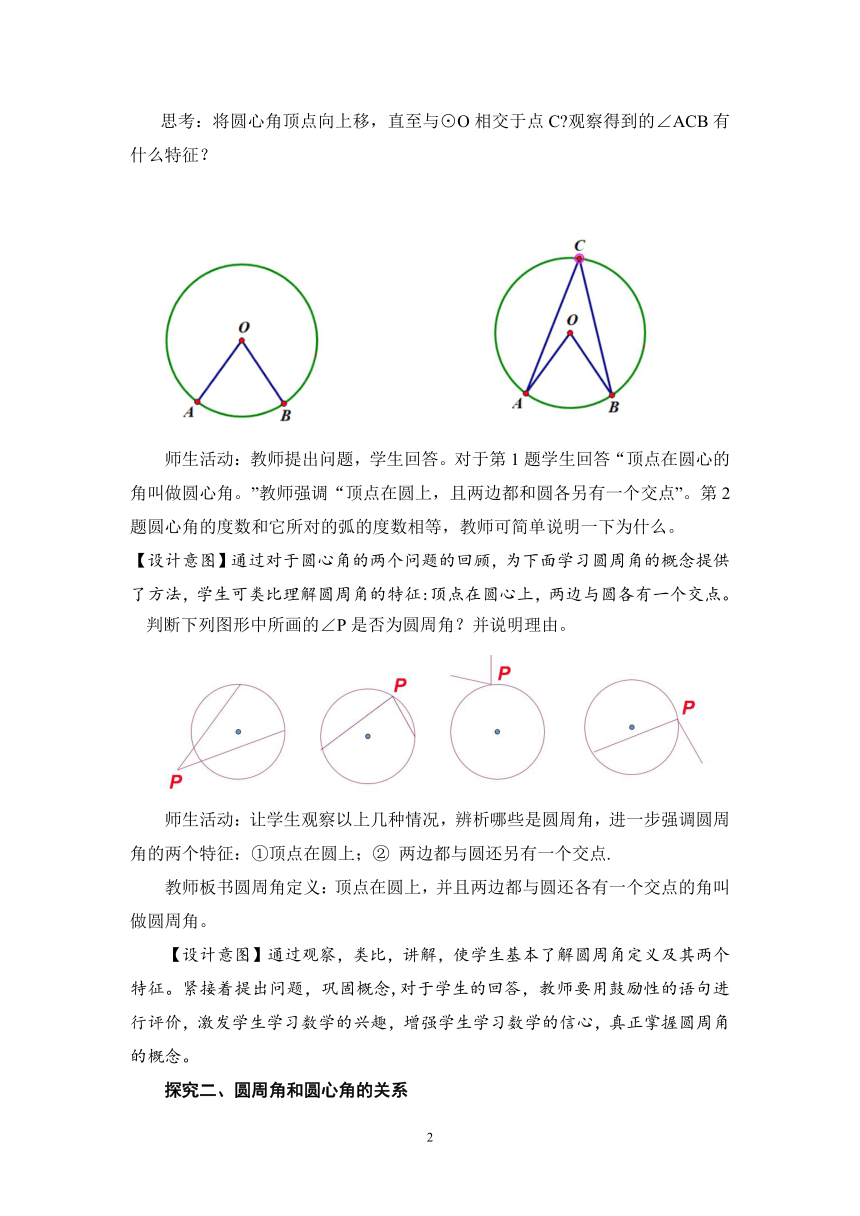
思考:将圆心角顶点向上移,直至与⊙O相交于点C 观察得到的∠ACB有什么特征?
师生活动:教师提出问题,学生回答。对于第1题学生回答“顶点在圆心的角叫做圆心角。”教师强调“顶点在圆上,且两边都和圆各另有一个交点”。第2题圆心角的度数和它所对的弧的度数相等,教师可简单说明一下为什么。
【设计意图】通过对于圆心角的两个问题的回顾,为下面学习圆周角的概念提供了方法,学生可类比理解圆周角的特征:顶点在圆心上,两边与圆各有一个交点。
师生活动:让学生观察以上几种情况,辨析哪些是圆周角,进一步强调圆周角的两个特征:①顶点在圆上;② 两边都与圆还另有一个交点.
教师板书圆周角定义:顶点在圆上,并且两边都与圆还各有一个交点的角叫做圆周角。
【设计意图】通过观察,类比,讲解,使学生基本了解圆周角定义及其两个特征。紧接着提出问题,巩固概念,对于学生的回答,教师要用鼓励性的语句进行评价,激发学生学习数学的兴趣,增强学生学习数学的信心,真正掌握圆周角的概念。
探究二、圆周角和圆心角的关系
数智技术融合设计
1. 第一课时:圆周角定理发现
活动1:动态观察与猜想
使用几何画板动态演示:拖动圆周角顶点,观察角与对应弧的关系。
问题链:
当圆心在圆周角内部/外部/边上时,圆周角与圆心角有何数量关系?
同弧所对的圆周角是否相等?
技术工具:几何画板、动态测量工具(实时显示角度数值)。
活动2:数据采集与验证
学生分组操作几何画板,记录不同位置圆周角与圆心角的度数,填写电子实验报告(如Google Forms)。
技术工具:数据可视化工具(生成角度关系图表)。
2. 第二课时:定理证明与分类讨论
活动1:辅助线智能提示
通过几何画板提供辅助线添加提示,引导学生完成三种位置关系的证明。
技术工具:分步动画演示、错误提示系统。
活动2:虚拟实验与协作学习
使用Mentimeter实时收集学生证明思路,运用Xmind生成思维导图,全班协作优化证明过程。
技术工具:Mentimeter、Xmind。
过程:如图,△ABC是等边三角形, ⊙O是其外接圆。你能发现∠BAC和∠BOC的大小有什么关系吗?
师生活动:教师投影,学生思考,得出结论:
∠A=∠BOC或∠BOC=2∠A.
即所对的圆周角等于它所对圆心角的一半.
学生结论的获得可能是通过度量也可能是推理,教师均给予鼓励.
教师画图并板书推理过程:
在图中
∵OA=OC,∴∠A=∠OCA.
又∠BOC=∠A+∠OCA=2∠A, ∴∠A=∠BOC.
教师提问:我们能否据此就说“一条弧所对的圆周角等于它所对圆心角的一半”
学生回答:不行,因为不能用特殊来代替一般。
教师提问:刚才我们看到的是圆心在圆周角一边时情形,那么圆心与圆周角的位置有哪些情形呢?
教师演示几何画板,让学生自主归纳得出:共有三种情形,即圆心在圆周角的一条边上,圆心在圆周角的内部和圆心在圆周角的外部。
教师投影出示圆心与圆周角的三种位置关系,并提问:另外两种情形中也有“所对的圆周角等于它所对圆心角的一半”吗?学生思考,教师在黑板上画
出图形。
教师引导学生把圆心在圆周角的内部和圆心在圆周角的外部这两种情形转化为第一种情形来证明,可让学生交流讨论完成推理过程.
教师板书证明过程:图(2)中,
连接AO并延长交⊙O于点D,再连接OB、OC,则由图(1)中结论可得:∠DAC=∠DOC,∠DAB=∠DOB.
∴∠BAC=∠DAC+∠DAB =∠DOC+∠DOB=∠COB.
在图(3)中,连接AO并延长交⊙O于点D,再连接OB、OC,
则由图(3)可得:∠DAC=∠DOC,∠DAB=∠DOB.
∴∠BAC=∠DAC-∠DAB=∠DOC-∠DOB=∠COB.
【设计意图】由特殊情形,提出猜想,使学生更容易自主探究,由特殊到一般,使探究的过程充满乐趣,增强了学生探究的信心。通过几何画板演示,揭示了圆周角与圆心位置关系只有三种情形,体现了分类讨论的数学思想。圆心在圆周角的内部和圆心在圆周角的外部两种情形的证明教师要引导学生运用圆心在圆周角一条边上的这一特殊情形的结论,适时渗透转化的数学思想。
定理归纳:由图(1)、图(2)和图(3)可知“在⊙O中,所对的圆周角总等于它所对圆心角的一半”
学生自主归纳,教师板书定理 .
教师板书圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
【设计意图】将圆心与圆周角位置关系的所有可能都考虑在内,三种情形都证明了猜想的正确性,最后归纳出圆周角定理,这实际上是完全归纳法。让学生学会正确表述定理,掌握用符号语言表达定理,理解定理表述的严密性,养成严谨的数学学习习惯,同时渗透分类讨论、从特殊到一般的数学思想。
探究三、同弧或等弧所对圆周角之间关系
类比猜想:“在同圆或等圆中,弧相等可得到圆心角相等,反之亦然”
在同圆或等圆中,圆周角与其所对的弧有什么关系?
师生活动:小组合作,猜想可能的结果,教师几何画板演示动画过程,学生进行验证。
问题1:同一条弧所对的圆周角∠C、∠D、∠E之间有什么关系?
问题2:等弧所对的∠C、∠F的大小有什么关系?为什么?
学生思考、证明,教师总结结论:同弧或等弧所对的圆周角相等。
教师继续追问:反过来,相等的圆周角和其所对弧有什么关系?引导学生分类讨论:相等的圆周角分别出现在同圆、等圆、半径不相等的圆中时,探讨其所对的弧的大小关系。教师几何画板展示三种情况:
第一种情况:在同圆中时,已知∠BAC=∠EDF,那么相等的圆周角所对的弧之间有什么关系?
第二种情况:在等圆中时,已知∠BAC=∠EDF,那么相等的圆周角所对的弧之间有什么关系?
第二种情况:在半径不相等的圆中时,已知∠BAC=∠EDF,那么相等的圆周角所对的弧之间有什么关系?
得出结论,教师板书在黑板上,圆周角推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等。
【设计意图】通过回顾之前圆周角定理及推论,类比猜想圆心角和所对弧之间的关系,通过应用刚学的圆周角定理进行证明,也让学生对刚学的知识点进行了巩固,同时渗透了分类讨论的数学思想,让学生学会了在考虑问题时要全面、细致。
随堂练习:
1.如图,四边形ABCD的四个顶点在⊙O上,找出图中分别与1、2、3、4相等的角。
【设计意图】通过练习,培养学生正确运用所学知识的应用能力,巩固所学的定理。
做一做:如图,AB是直径,C是圆上任意一点(不与A、B重合),求ACB °.
让学生根据所学知识,分析求出角度。
分析:因为∠ACB是弦AB(或半圆AB)所对的圆周角,根据圆周角定理可知,∠ACB等于∠AOB的一半,由于AB是直径,所以∠AOB=180°,从而推出2
∠ACB=90°。
教师继续追问:如果ACB90°,能得出AB是直径吗?
让学生思考,并提问学生进行分析、证明。
从而总结得出圆周角推论2,教师板书。圆周角推论2:半圆(或直径)所对的圆周角是直角, 90°的圆周角所对的弦是直径。
【设计意图】再进一步探究圆周角性质时,学生可根据已学的圆周角定理和推论自行证明,让学生学会了知识的转化和应用。
【应用新知】
例1 如图,AB为⊙O的直径,弦CD交AB于点P,ACD60°,ADC70°. 求∠APC的度数。
【设计意图】通过习题,巩固刚学的定理和推论,提升学生对知识的把握和综合应用能力。
【智能分层练习】
基于Kahoot!平台推送分层习题,系统自动批改并生成个性化错题本。
技术工具:Kahoot!、AI错题分析系统。
【设计意图】巩固和检验所学知识,使学生得到提高和发展。
【评价与反馈】
过程性评价:通过ClassDojo记录学生课堂参与度与探究表现。
结果性评价:在线测试(如Quizizz)评估知识掌握情况,系统生成班级能力雷达图。
技术赋能反馈:利用数据分析平台(如Power BI)可视化学习轨迹,调整后续教学策略。
【教学反思与优化】
技术融合点:动态演示降低抽象难度,协作工具促进深度学习,数据反馈实现精准教学。
改进方向:增加VR几何实验模块,进一步提升空间想象能力。
判断下列图形中所画的∠P是否为圆周角?并说明理由。
PAGE
9
第1课时 圆周角定理及推论
一、教学目标
1.理解圆周角的概念,学会识别圆周角;
2.了解圆周角与圆心角的关系,能够理解和掌握圆周角定理及推论,并进行简单的计算与证明。
3. 通过几何画板动态演示,观察圆周角与圆心角的关系,经历猜想-验证-归纳的探究过程。运用数智工具辅助分类讨论,突破定理证明难点。
二、教学重难点
重点:了解圆周角与圆心角的关系.
难点:能够理解和掌握圆周角定理及推论,并进行简单的计算与证明.
三、教学用具
多媒体、课件、几何画板
四、教学过程
【旧识回顾】
【设计意图】帮助学生梳理所学知识,了解知识点联系,有助于本节课的学习。
【新知探究】
探究一、圆周角的概念
思考:将圆心角顶点向上移,直至与⊙O相交于点C 观察得到的∠ACB有什么特征?
师生活动:教师提出问题,学生回答。对于第1题学生回答“顶点在圆心的角叫做圆心角。”教师强调“顶点在圆上,且两边都和圆各另有一个交点”。第2题圆心角的度数和它所对的弧的度数相等,教师可简单说明一下为什么。
【设计意图】通过对于圆心角的两个问题的回顾,为下面学习圆周角的概念提供了方法,学生可类比理解圆周角的特征:顶点在圆心上,两边与圆各有一个交点。
师生活动:让学生观察以上几种情况,辨析哪些是圆周角,进一步强调圆周角的两个特征:①顶点在圆上;② 两边都与圆还另有一个交点.
教师板书圆周角定义:顶点在圆上,并且两边都与圆还各有一个交点的角叫做圆周角。
【设计意图】通过观察,类比,讲解,使学生基本了解圆周角定义及其两个特征。紧接着提出问题,巩固概念,对于学生的回答,教师要用鼓励性的语句进行评价,激发学生学习数学的兴趣,增强学生学习数学的信心,真正掌握圆周角的概念。
探究二、圆周角和圆心角的关系
数智技术融合设计
1. 第一课时:圆周角定理发现
活动1:动态观察与猜想
使用几何画板动态演示:拖动圆周角顶点,观察角与对应弧的关系。
问题链:
当圆心在圆周角内部/外部/边上时,圆周角与圆心角有何数量关系?
同弧所对的圆周角是否相等?
技术工具:几何画板、动态测量工具(实时显示角度数值)。
活动2:数据采集与验证
学生分组操作几何画板,记录不同位置圆周角与圆心角的度数,填写电子实验报告(如Google Forms)。
技术工具:数据可视化工具(生成角度关系图表)。
2. 第二课时:定理证明与分类讨论
活动1:辅助线智能提示
通过几何画板提供辅助线添加提示,引导学生完成三种位置关系的证明。
技术工具:分步动画演示、错误提示系统。
活动2:虚拟实验与协作学习
使用Mentimeter实时收集学生证明思路,运用Xmind生成思维导图,全班协作优化证明过程。
技术工具:Mentimeter、Xmind。
过程:如图,△ABC是等边三角形, ⊙O是其外接圆。你能发现∠BAC和∠BOC的大小有什么关系吗?
师生活动:教师投影,学生思考,得出结论:
∠A=∠BOC或∠BOC=2∠A.
即所对的圆周角等于它所对圆心角的一半.
学生结论的获得可能是通过度量也可能是推理,教师均给予鼓励.
教师画图并板书推理过程:
在图中
∵OA=OC,∴∠A=∠OCA.
又∠BOC=∠A+∠OCA=2∠A, ∴∠A=∠BOC.
教师提问:我们能否据此就说“一条弧所对的圆周角等于它所对圆心角的一半”
学生回答:不行,因为不能用特殊来代替一般。
教师提问:刚才我们看到的是圆心在圆周角一边时情形,那么圆心与圆周角的位置有哪些情形呢?
教师演示几何画板,让学生自主归纳得出:共有三种情形,即圆心在圆周角的一条边上,圆心在圆周角的内部和圆心在圆周角的外部。
教师投影出示圆心与圆周角的三种位置关系,并提问:另外两种情形中也有“所对的圆周角等于它所对圆心角的一半”吗?学生思考,教师在黑板上画
出图形。
教师引导学生把圆心在圆周角的内部和圆心在圆周角的外部这两种情形转化为第一种情形来证明,可让学生交流讨论完成推理过程.
教师板书证明过程:图(2)中,
连接AO并延长交⊙O于点D,再连接OB、OC,则由图(1)中结论可得:∠DAC=∠DOC,∠DAB=∠DOB.
∴∠BAC=∠DAC+∠DAB =∠DOC+∠DOB=∠COB.
在图(3)中,连接AO并延长交⊙O于点D,再连接OB、OC,
则由图(3)可得:∠DAC=∠DOC,∠DAB=∠DOB.
∴∠BAC=∠DAC-∠DAB=∠DOC-∠DOB=∠COB.
【设计意图】由特殊情形,提出猜想,使学生更容易自主探究,由特殊到一般,使探究的过程充满乐趣,增强了学生探究的信心。通过几何画板演示,揭示了圆周角与圆心位置关系只有三种情形,体现了分类讨论的数学思想。圆心在圆周角的内部和圆心在圆周角的外部两种情形的证明教师要引导学生运用圆心在圆周角一条边上的这一特殊情形的结论,适时渗透转化的数学思想。
定理归纳:由图(1)、图(2)和图(3)可知“在⊙O中,所对的圆周角总等于它所对圆心角的一半”
学生自主归纳,教师板书定理 .
教师板书圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
【设计意图】将圆心与圆周角位置关系的所有可能都考虑在内,三种情形都证明了猜想的正确性,最后归纳出圆周角定理,这实际上是完全归纳法。让学生学会正确表述定理,掌握用符号语言表达定理,理解定理表述的严密性,养成严谨的数学学习习惯,同时渗透分类讨论、从特殊到一般的数学思想。
探究三、同弧或等弧所对圆周角之间关系
类比猜想:“在同圆或等圆中,弧相等可得到圆心角相等,反之亦然”
在同圆或等圆中,圆周角与其所对的弧有什么关系?
师生活动:小组合作,猜想可能的结果,教师几何画板演示动画过程,学生进行验证。
问题1:同一条弧所对的圆周角∠C、∠D、∠E之间有什么关系?
问题2:等弧所对的∠C、∠F的大小有什么关系?为什么?
学生思考、证明,教师总结结论:同弧或等弧所对的圆周角相等。
教师继续追问:反过来,相等的圆周角和其所对弧有什么关系?引导学生分类讨论:相等的圆周角分别出现在同圆、等圆、半径不相等的圆中时,探讨其所对的弧的大小关系。教师几何画板展示三种情况:
第一种情况:在同圆中时,已知∠BAC=∠EDF,那么相等的圆周角所对的弧之间有什么关系?
第二种情况:在等圆中时,已知∠BAC=∠EDF,那么相等的圆周角所对的弧之间有什么关系?
第二种情况:在半径不相等的圆中时,已知∠BAC=∠EDF,那么相等的圆周角所对的弧之间有什么关系?
得出结论,教师板书在黑板上,圆周角推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等。
【设计意图】通过回顾之前圆周角定理及推论,类比猜想圆心角和所对弧之间的关系,通过应用刚学的圆周角定理进行证明,也让学生对刚学的知识点进行了巩固,同时渗透了分类讨论的数学思想,让学生学会了在考虑问题时要全面、细致。
随堂练习:
1.如图,四边形ABCD的四个顶点在⊙O上,找出图中分别与1、2、3、4相等的角。
【设计意图】通过练习,培养学生正确运用所学知识的应用能力,巩固所学的定理。
做一做:如图,AB是直径,C是圆上任意一点(不与A、B重合),求ACB °.
让学生根据所学知识,分析求出角度。
分析:因为∠ACB是弦AB(或半圆AB)所对的圆周角,根据圆周角定理可知,∠ACB等于∠AOB的一半,由于AB是直径,所以∠AOB=180°,从而推出2
∠ACB=90°。
教师继续追问:如果ACB90°,能得出AB是直径吗?
让学生思考,并提问学生进行分析、证明。
从而总结得出圆周角推论2,教师板书。圆周角推论2:半圆(或直径)所对的圆周角是直角, 90°的圆周角所对的弦是直径。
【设计意图】再进一步探究圆周角性质时,学生可根据已学的圆周角定理和推论自行证明,让学生学会了知识的转化和应用。
【应用新知】
例1 如图,AB为⊙O的直径,弦CD交AB于点P,ACD60°,ADC70°. 求∠APC的度数。
【设计意图】通过习题,巩固刚学的定理和推论,提升学生对知识的把握和综合应用能力。
【智能分层练习】
基于Kahoot!平台推送分层习题,系统自动批改并生成个性化错题本。
技术工具:Kahoot!、AI错题分析系统。
【设计意图】巩固和检验所学知识,使学生得到提高和发展。
【评价与反馈】
过程性评价:通过ClassDojo记录学生课堂参与度与探究表现。
结果性评价:在线测试(如Quizizz)评估知识掌握情况,系统生成班级能力雷达图。
技术赋能反馈:利用数据分析平台(如Power BI)可视化学习轨迹,调整后续教学策略。
【教学反思与优化】
技术融合点:动态演示降低抽象难度,协作工具促进深度学习,数据反馈实现精准教学。
改进方向:增加VR几何实验模块,进一步提升空间想象能力。
判断下列图形中所画的∠P是否为圆周角?并说明理由。
PAGE
9
