5.3.1密度的简单计算-2025-2026学年沪粤版物理八年级上册教学课件(52页PPT)
文档属性
| 名称 | 5.3.1密度的简单计算-2025-2026学年沪粤版物理八年级上册教学课件(52页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪粤版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-13 07:53:47 | ||
图片预览









文档简介
(共52张PPT)
5.3.1密度的简单计算
第五章 质量与密度
沪粤版2025-2026学年 物理八年级上册【精做课件】
授课教师:********
班 级:********
时 间:********
5.3.1 密度的简单计算
教学目标
能熟练运用密度公式 ρ=m/V 及变形公式 m=ρV、V=m/ρ 进行简单计算。(重点)
学会分析题目中的已知条件和所求量,选择合适的公式进行计算。
掌握单位换算在密度计算中的应用,确保计算过程中单位统一。(难点)
能运用密度计算解决生活中的简单实际问题,体会密度知识的实用性。
密度公式及变形
基本公式
密度的定义公式为:ρ = m / V
其中,ρ 表示物质的密度,单位为 kg/m 或 g/cm ;m 表示物体的质量,单位为 kg 或 g;V 表示物体的体积,单位为 m 或 cm 。
变形公式
已知密度和体积,求质量:m = ρV
已知密度和质量,求体积:V = m / ρ
单位换算要点
在计算过程中,需保证单位统一:
当密度单位为 kg/m 时,质量单位对应 kg,体积单位对应 m ;
当密度单位为 g/cm 时,质量单位对应 g,体积单位对应 cm ;
常用换算关系:1g/cm = 10 kg/m ,1m = 10 cm ,1kg = 10 g。
常见题型及例题解析
题型一:已知质量和体积,求密度
例题 1:一块长方体铁块,质量为 7.9kg,体积为 1dm ,求铁块的密度。
解析:
已知:m = 7.9kg,V = 1dm = 1×10 m (单位换算:1dm = 10 m )
求:ρ
解:根据 ρ = m / V,代入数据得:
ρ = 7.9kg / 1×10 m = 7.9×10 kg/m
答:铁块的密度为 7.9×10 kg/m 。
例题 2:一个装满水的烧杯,总质量为 350g,将一个质量为 50g 的石块放入水中,溢出部分水后,总质量为 380g,求石块的密度。
解析:
关键:先求出石块的体积(等于溢出水的体积)
溢出水的质量:m 溢 = 350g + 50g - 380g = 20g
水的密度 ρ 水 = 1g/cm ,由 V = m/ρ 得溢出水的体积:
V 溢 = 20g / 1g/cm = 20cm ,即石块体积 V = 20cm
石块密度:ρ = m / V = 50g / 20cm = 2.5g/cm = 2.5×10 kg/m
答:石块的密度为 2.5×10 kg/m 。
题型二:已知密度和体积,求质量
例题 3:一个容积为 50L 的油箱,装满了密度为 0.71×10 kg/m 的汽油,求油箱内汽油的质量。
解析:
已知:V = 50L = 50dm = 0.05m (单位换算:1L = 1dm = 10 m ),ρ = 0.71×10 kg/m
求:m
解:根据 m = ρV,代入数据得:
m = 0.71×10 kg/m × 0.05m = 35.5kg
答:油箱内汽油的质量为 35.5kg。
题型三:已知密度和质量,求体积
例题 4:一个质量为 1.32kg 的铜球,已知铜的密度为 8.9×10 kg/m ,求这个铜球的体积。
解析:
已知:m = 1.32kg,ρ = 8.9×10 kg/m
求:V
解:根据 V = m / ρ,代入数据得:
V = 1.32kg / 8.9×10 kg/m ≈ 0.148×10 m = 148cm
答:这个铜球的体积约为 148cm 。
题型四:结合物体实心、空心的判断
例题 5:一个铝球的质量为 54g,体积为 30cm ,铝的密度为 2.7g/cm ,判断该铝球是否为空心?若为空心,空心部分体积是多少?
解析:
步骤 1:假设铝球为实心,计算其体积:
V 实 = m / ρ = 54g / 2.7g/cm = 20cm
步骤 2:比较实际体积与实心体积:
因 30cm > 20cm ,故铝球为空心。
步骤 3:计算空心部分体积:
V 空 = V 实 - V 球 = 30cm - 20cm = 10cm
答:该铝球是空心的,空心部分体积为 10cm 。
计算注意事项
单位统一:计算前需将质量、体积的单位换算为与密度单位匹配的单位(如 ρ 用 kg/m 时,m 用 kg,V 用 m )。
公式选择:根据已知量和未知量,灵活选择 ρ=m/V、m=ρV 或 V=m/ρ,避免公式混淆。
规范步骤:写出已知条件、所求量、公式,代入数据(带单位),计算结果(保留合理小数位数),最后作答。
隐含条件挖掘:如 “装满液体” 表示液体体积等于容器容积;“物体浸没” 表示物体体积等于排开液体体积。
课堂练习
一块体积为 20cm 的大理石,质量为 50g,求大理石的密度(结果保留两位小数)。
已知水的密度为 1×10 kg/m ,一个蓄水池的容积为 500m ,求该蓄水池装满水时水的质量。
某品牌食用油的密度为 0.9×10 kg/m ,一瓶 5L 装的该食用油质量是多少 kg?
一个质量为 117g 的铁球,体积为 20cm (ρ 铁 = 7.9g/cm ),判断该铁球是否为空心?若空心,空心部分体积多大?
课堂总结
密度计算的核心是灵活运用基本公式 ρ=m/V 及变形公式 m=ρV、V=m/ρ。
计算时必须保证单位统一,明确各物理量的单位换算关系。
解决实际问题时,需先分析已知条件,挖掘隐含信息(如体积相等、质量关系等),再选择合适公式计算。
通过密度计算可以解决物质鉴别、质量 / 体积估算、物体实心空心判断等问题,体现了密度知识在生活中的实用价值。
课后作业
一个长方体木块,长 5cm、宽 4cm、高 3cm,质量为 120g,求木块的密度。
修建一座桥需要用密度为 2.5×10 kg/m 的石料 500m ,这些石料的总质量是多少吨?
一个空瓶的质量为 200g,装满水后总质量为 700g,若装满某种液体后总质量为 600g,求该液体的密度。
查阅资料,找到你家所用防盗门的材质及密度,测量其长、宽、厚,估算防盗门的质量。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.密度的公式?
2.水的密度是多少?表示什么含义?
3.知道了密度公式中的任意两个,如何求第三个量?
复习与回顾
求质量
求体积
鉴别物质
一、密度公式应用
应用类型 应用公式 适用情境
求密度 ρ = 测物质密度、鉴别物质
求质量 m =ρV 求质量不易直接测量的物体的质量(如高大的石碑、油罐车中的油、成堆的粮食)
求体积 V = 求不便直接测量体积的物体的体积(如铜线的体积、不规则容器的容积等)
一、密度公式应用
1.某地有一水库,如图所示,已知它的最大容积为7.5×106m3,那么,这个水库最多可以积蓄多少吨水?
练一练
解:m=ρV=1.0×103kg/m3×7.5×106m3
=7.5×106kg
=7.5×106t
一、密度公式应用
例2:例某城市有一座大理石雕塑,如图所示,已知其质量为18.5t,它的体积是多少?
一、密度公式应用
物质名称 密度 物质名称 密度
锇 铝
金 大理石
铅 砖
银 冰
铜 蜡
钢、铁 干松木
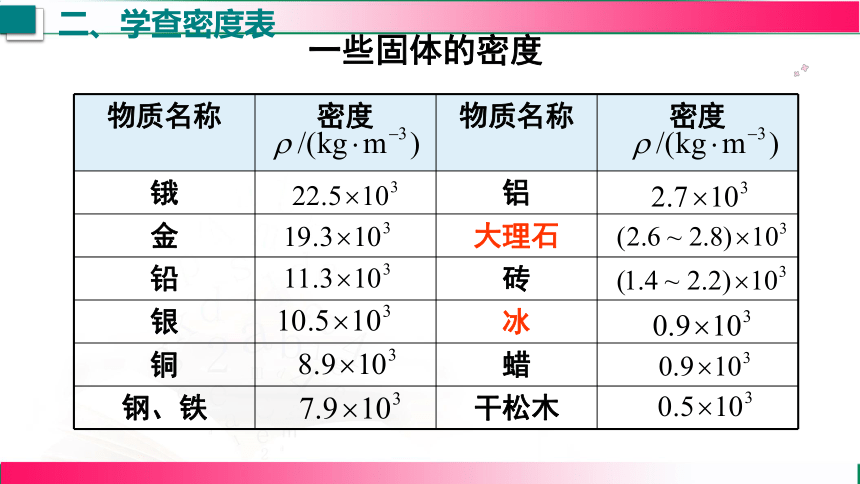
一些固体的密度
二、学查密度表
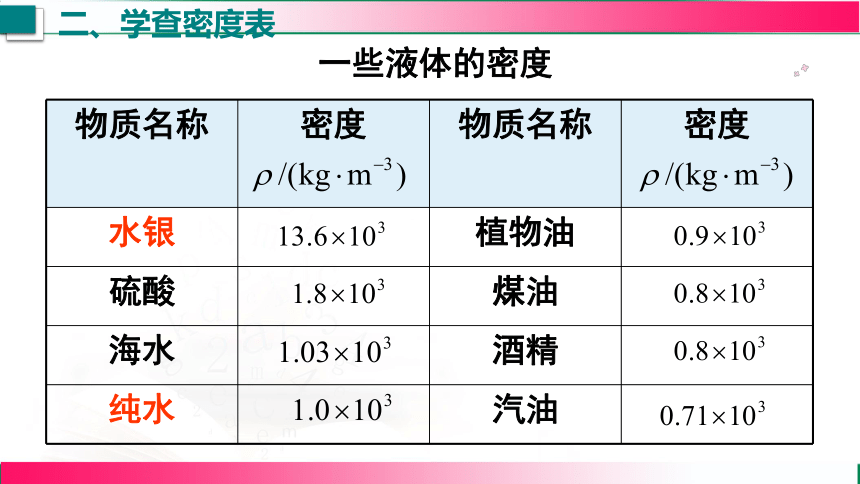
一些液体的密度
物质名称 密度 物质名称 密度
水银 植物油
硫酸 煤油
海水 酒精
纯水 汽油
二、学查密度表
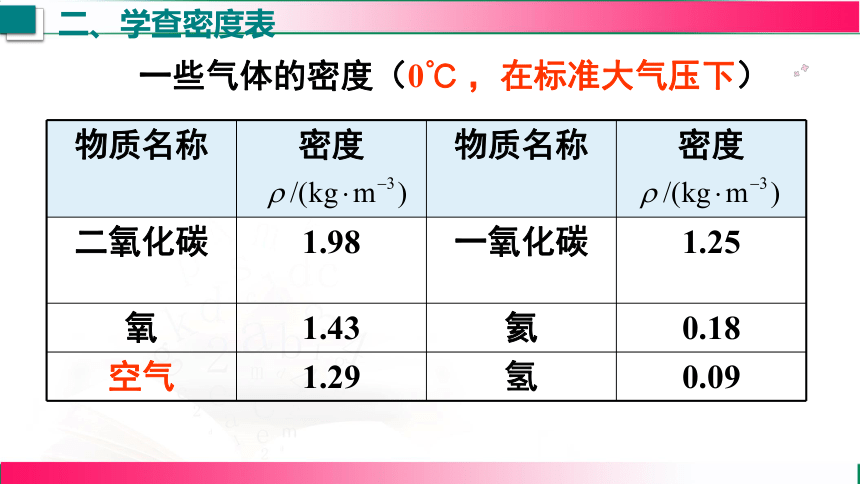
一些气体的密度(0℃ ,在标准大气压下)
物质名称 密度 物质名称 密度
二氧化碳 1.98 一氧化碳 1.25
氧 1.43 氦 0.18
空气 1.29 氢 0.09
二、学查密度表
1.一般:ρ固>ρ液>ρ气 ;
2.一些物质密度相同:如冰和蜡,酒精和煤油;
3.同种物质物态不同密度可能不同:如冰和水;
4.固体和液体密度用国际单位,数值都表示为“×103 ”的形式,如ρ水=1.0×103 kg/m3 ;气体密度用国际单位,数值没有“×103”,如 ρ空气=1.29 kg/m3。
观察表中数据能发现一些规律吗?
二、学查密度表
例1:如图所示,一枚第25届奥运会的纪念币,它的质量为16.1g,体积为1.8cm3。试求制成这种纪念币的金属的密度,并从密度表中找出它是那种金属。
已知:纪念币的质量m=16.1g=1.61×10-2kg,纪念币的体积V=1.8cm3=1.8×10-6m3。
求:制成纪念币的金属的密度ρ。
答:制成纪念币的金属的密度为8.9×103kg/m3。
查密度表可知纪念币是铜币
二、学查密度表
1.比例题
例1 甲、乙两种物质密度之比是3:2,质量之比是
2:1,求它们的体积之比。
三、密度计算应用
2.巧妙测量
例2 一只空瓶质量是0.2kg,装满水后总质量是1.0kg,倒掉水后再装满另一种液体,总质量是1.64kg,求这种液体的密度。
分析:该液体的密度要用它的质量与其体积之比求得,而其质量等于液体与瓶的总质量减去瓶的质量,其体积等于瓶的容积,也等于水的体积,水的体积等于水的质量除以水的密度,而水的质量又等于水和瓶的总质量减去瓶的质量。
三、密度计算应用
解题心得归纳:
解这类题时要抓住同一个瓶子装满不同的液体其容积不变。
三、密度计算应用
例3 为了测定某种小钢球的密度,先在一只空瓶中装满水,测得总质量是540g,然后将质量是97.5g的小钢球装入瓶内,溢出一部分水后,再测其总质量是625g,求这种小钢球的密度。
分析:因为题中已经给出了钢球的质量,要求钢球的密度,关键是求出小钢球的体积.小钢球的体积等于钢球排出的水的体积。只要求出钢球排出的水的质量,利用密度变形公式就可以求出水的体积。而排出的水的质量可以这样求:用原来满瓶水和瓶的总质量减去剩下的水和瓶的总质量即可。
三、密度计算应用
三、密度计算应用
例4 学校安装电路需用铜线,手头有一卷铜线,其质量为178kg,横截面积为2.5mm2,则这卷铜线有多长?
分析:要求铜线的长,则必须知道铜线的体积,然后根据V=SL求出长度。
三、密度计算应用
3.合金问题
例5 金、银合金的质量是530g,体积是35cm3,则金、银各有多少克?
分析
合金问题要抓住的思路。
三、密度计算应用
三、密度计算应用
例6 某实验室需要密度是1.1×103kg/m3 的盐水.现配制了0.5dm3的盐水,称得盐水的质量是0.6kg,这种盐水是否符合要求?若不符合要求,应该加盐还是加水?加多少?
分析:先求出盐水的密度,然后与标准盐水的密度进行比较,如果等于标准盐水密度,那么就符合要求。如果大于或小于标准盐水密度,就都不符合要求。若大于标准盐水密度,则应加水;若小于标准盐水密度,则应加盐。
三、密度计算应用
三、密度计算应用
5.选材问题
例9 一位飞机设计师,为减轻飞机的重力,要把一个钢制零件换成铝制零件,使其质量减少104kg,则这个零件共需铝多少千克?
分析:
钢制零件换成铝制零件其体积不变。
三、密度计算应用
三、密度计算应用
知识点1 密度公式的应用
1.母题 教材P133信息浏览 现代宇宙科学告诉我们,恒星在
演变过程中会形成密度很大的天体,如中子星、黑洞等。据
推测中子星的质量约为__________ ,则
中子星的密度约为__________ 。
返回
2.[2024·合肥蜀山区模拟]已知原来烧杯中盛有的酒精和烧
杯的总质量为 ,将部分酒精倒入量筒后,剩余的酒精与
烧杯的总质量如图甲所示,倒入量筒中的酒精的体积如图乙
所示,则可计算该酒精的密度为___________ 。
【点拨】图甲中剩余的酒精与烧杯的总质量
,量筒中酒精的质量
,由图乙可知,量筒的
分度值是,量筒中酒精的体积 ,酒
精的密度 。
返回
3.质量为的空瓶,装满水后的总质量为 ,瓶的容
积为_______。该瓶最多能装质量为 的某液体,此
液体的密度为__________。(水的密度为 )
1 500
【点拨】瓶子装满水后,水的质量
,瓶子的容积
,该瓶最多能装质量为
的某液体,此液体的密度
。
返回
4.过年小明收到了一份特殊的“压岁钱”——一两的银元宝。
小明给一个碗里装入适量水并测出总质量为 ,再将银元
宝浸没在水中,在水面处标上标记,测出总质量为 。将
银元宝从水中取出,再向碗里加水到标记处,测出总质量为
。银元宝的体积是___ ;银元宝的密度是_________
;所测的密度值______(填“偏大”“偏小”或“准确”)。
5
准确
【点拨】由题意得,将银元宝从水中取出,再向碗里加水,
所加水的体积即为银元宝的体积。所加水的质量
,银元宝的体积
; 据题知,银元宝的质量
,所以银元宝的密度
,虽然将银元
宝拿出时带走了一部分水,但是再补水至标记处时被带走的
水又会被补充回来,所以结果仍然准确。
返回
5.为了测饮料的密度,小军进行了如下操作:他找了一个玻
璃瓶,测出其质量为 ,将其盛满水测得总质量
为 ,然后把水倒干净,盛满饮料测得总质量为
。(水的密度为 )求:
(1)玻璃瓶的容积。
【解】玻璃瓶装满水后水的质量
,
由 可得,水的体积
,玻璃瓶的容积
。
(2)饮料的密度。
【解】饮料的质量
,
饮料的体积 ,
饮料的密度 。
(3)一个标有“ ”的塑料瓶,最多能盛多少千克这种饮料?
【解】一个标有“ ”的塑料瓶,最多能盛饮料的体积
,
最多盛饮料的质量
。
返回
知识点2 密度表与物质鉴别
6. [2024·北京西城区期中]下表是常温常压下部分物质的
密度值。根据表格中信息,下列说法正确的是( )
金 汞
铜 纯水
钢、铁 植物油
酒精
A. 固体的密度一定比液体的密度大
B. 体积相同的植物油和酒精,酒精的质量大
C. 质量相同的实心铜块和铁块,铁块的体积大
D. 不同物质的密度一定不同
√
【点拨】由表格数据可知,冰的密度小于纯水的密度,因此
固体的密度不一定比液体的密度大,故A错误;由表格数据
可知,植物油的密度大于酒精的密度,由 可知,体积
相同的植物油和酒精相比,植物油质量大,故B错误;由表
格数据可知,铜的密度大于铁的密度,由 可知,质量
相同的实心铜块和铁块相比,铁块的体积大,故C正确;由
表格数据可知,冰和植物油的密度相同,因此不同物质的密
度可能相同,故D错误。
返回
7.“摘星星”的妈妈王亚平从空间站回到地球,把自己从太空
摘的“星星”送给了女儿。若这枚来自太空的实心星星纪念币
的质量为,体积为 ,则这枚纪念币的密度是
__________ ,______(填“是”或“不是”)纯金制成
的。
不是
【点拨】根据 得,纪念币的密度
,已知
, ,故该纪念币不是用纯金制
成的。
返回
纠易错 不能正确计算混合物体的密度
8. 由质量相等的甲、乙两种金属制成合金块,两种金属的密
度分别为和 ,若总体积不变,则合金块的密度为( )
C
A. B. C. D.
【点拨】设甲、乙两金属的质量均为 ,则两金属的体积分
别为, ,合金块的密度
。
返回
9. 如图所示,天平已调平,将4个相同的甲球和5个相同的乙
球按图示摆放至天平左右两盘时,天平仍平衡,已知甲球和
乙球的体积相同,下列说法正确的是( )
D
(第9题)
A. 1个甲球与1个乙球的质量之比为
B. 3个甲球与4个乙球的质量之比为
C. 甲球与乙球的密度之比为
D. 甲球与乙球的密度之比为
(第9题)
【点拨】由题意和图示可得,
,整理可得
,即1个甲球与1个乙球
的质量之比为 ,故A错误;3个甲球
与4个乙球的质量之比为 ,
故B错误;已知,由 可得,甲、乙两球的密度
之比 ,故C错误,D正确。
返回
(第10题)
10.[2025·合肥专题练习]某医院 重症
监护室内配有充满氧气的钢瓶,其总质量
为,瓶内氧气的密度为;使用 后,
总质量变为 ,瓶内氧气的密度变为
; 再使用一段时间后,总质量变为
20
,则此时瓶内氧气的密度为_____,氧气瓶的质量是
____ 。如图所示为某物质的密度与体积的关系,则阴影部
分的面积 表示的物理量的值为_____。
(第10题)
【点拨】设氧气瓶的质量为 ,其容积为
,则由 可得,刚启用时瓶内氧气的
密度 ,使用1小时,总质量
变为 ,而氧气的体积不变(等于氧气
瓶的容积),此时瓶内氧气的密度为
, 解得氧气瓶的质量
,总质量为 的氧气瓶,最
初氧气的质量为 ,再
使用一段时间,总质量变为 ,则此时
瓶内氧气的质量为 ,
氧气的体积一定,根据 可知,氧气的
密度和氧气的质量成正比,所以,此时瓶
(第10题)
内的氧气密度应为原来的,应为 。
分析图像中的横坐标和纵坐标可知,横坐
标表示体积,纵坐标表示密度,故此时阴
影部分的面积 ,即为该物质的质量,
则 。
(第10题)
返回
11.[2025·盐城期末]走到刚下的积雪上面,感觉很松软。
小宇用一个带有刻度的容器收集了 积雪,用电子秤
测得该容器装雪前后质量之差为 。问:
(1)小宇采集的积雪的密度是多少克每立方厘米?
【解】积雪密度 。
(2)若组成雪花的冰晶密度为 ,则小宇采集的积
雪中,空心的体积占了多少?(用百分比表示)
【解】组成雪花的冰晶的体积 ,
空心的体积 ,
空心的体积占比为 。
(3)查阅资料发现,降雪量是指将雪熔化后,以毫米为计
量单位的水的深度。小宇测出地面上积雪平均厚度为 ,
则本次降雪量大小是多少?
【解】雪熔化前后质量不变,有,由 得,
,则 ,
,代入得
,解得
。
返回
密度知识的应用
密度表
密度知识的应用
固体、液体、气体的密度
比例题
巧妙测量
冰和水的问题
合金问题
选材问题
用密度知识解释生活中的常见现象
课堂小结
谢谢观看!
5.3.1密度的简单计算
第五章 质量与密度
沪粤版2025-2026学年 物理八年级上册【精做课件】
授课教师:********
班 级:********
时 间:********
5.3.1 密度的简单计算
教学目标
能熟练运用密度公式 ρ=m/V 及变形公式 m=ρV、V=m/ρ 进行简单计算。(重点)
学会分析题目中的已知条件和所求量,选择合适的公式进行计算。
掌握单位换算在密度计算中的应用,确保计算过程中单位统一。(难点)
能运用密度计算解决生活中的简单实际问题,体会密度知识的实用性。
密度公式及变形
基本公式
密度的定义公式为:ρ = m / V
其中,ρ 表示物质的密度,单位为 kg/m 或 g/cm ;m 表示物体的质量,单位为 kg 或 g;V 表示物体的体积,单位为 m 或 cm 。
变形公式
已知密度和体积,求质量:m = ρV
已知密度和质量,求体积:V = m / ρ
单位换算要点
在计算过程中,需保证单位统一:
当密度单位为 kg/m 时,质量单位对应 kg,体积单位对应 m ;
当密度单位为 g/cm 时,质量单位对应 g,体积单位对应 cm ;
常用换算关系:1g/cm = 10 kg/m ,1m = 10 cm ,1kg = 10 g。
常见题型及例题解析
题型一:已知质量和体积,求密度
例题 1:一块长方体铁块,质量为 7.9kg,体积为 1dm ,求铁块的密度。
解析:
已知:m = 7.9kg,V = 1dm = 1×10 m (单位换算:1dm = 10 m )
求:ρ
解:根据 ρ = m / V,代入数据得:
ρ = 7.9kg / 1×10 m = 7.9×10 kg/m
答:铁块的密度为 7.9×10 kg/m 。
例题 2:一个装满水的烧杯,总质量为 350g,将一个质量为 50g 的石块放入水中,溢出部分水后,总质量为 380g,求石块的密度。
解析:
关键:先求出石块的体积(等于溢出水的体积)
溢出水的质量:m 溢 = 350g + 50g - 380g = 20g
水的密度 ρ 水 = 1g/cm ,由 V = m/ρ 得溢出水的体积:
V 溢 = 20g / 1g/cm = 20cm ,即石块体积 V = 20cm
石块密度:ρ = m / V = 50g / 20cm = 2.5g/cm = 2.5×10 kg/m
答:石块的密度为 2.5×10 kg/m 。
题型二:已知密度和体积,求质量
例题 3:一个容积为 50L 的油箱,装满了密度为 0.71×10 kg/m 的汽油,求油箱内汽油的质量。
解析:
已知:V = 50L = 50dm = 0.05m (单位换算:1L = 1dm = 10 m ),ρ = 0.71×10 kg/m
求:m
解:根据 m = ρV,代入数据得:
m = 0.71×10 kg/m × 0.05m = 35.5kg
答:油箱内汽油的质量为 35.5kg。
题型三:已知密度和质量,求体积
例题 4:一个质量为 1.32kg 的铜球,已知铜的密度为 8.9×10 kg/m ,求这个铜球的体积。
解析:
已知:m = 1.32kg,ρ = 8.9×10 kg/m
求:V
解:根据 V = m / ρ,代入数据得:
V = 1.32kg / 8.9×10 kg/m ≈ 0.148×10 m = 148cm
答:这个铜球的体积约为 148cm 。
题型四:结合物体实心、空心的判断
例题 5:一个铝球的质量为 54g,体积为 30cm ,铝的密度为 2.7g/cm ,判断该铝球是否为空心?若为空心,空心部分体积是多少?
解析:
步骤 1:假设铝球为实心,计算其体积:
V 实 = m / ρ = 54g / 2.7g/cm = 20cm
步骤 2:比较实际体积与实心体积:
因 30cm > 20cm ,故铝球为空心。
步骤 3:计算空心部分体积:
V 空 = V 实 - V 球 = 30cm - 20cm = 10cm
答:该铝球是空心的,空心部分体积为 10cm 。
计算注意事项
单位统一:计算前需将质量、体积的单位换算为与密度单位匹配的单位(如 ρ 用 kg/m 时,m 用 kg,V 用 m )。
公式选择:根据已知量和未知量,灵活选择 ρ=m/V、m=ρV 或 V=m/ρ,避免公式混淆。
规范步骤:写出已知条件、所求量、公式,代入数据(带单位),计算结果(保留合理小数位数),最后作答。
隐含条件挖掘:如 “装满液体” 表示液体体积等于容器容积;“物体浸没” 表示物体体积等于排开液体体积。
课堂练习
一块体积为 20cm 的大理石,质量为 50g,求大理石的密度(结果保留两位小数)。
已知水的密度为 1×10 kg/m ,一个蓄水池的容积为 500m ,求该蓄水池装满水时水的质量。
某品牌食用油的密度为 0.9×10 kg/m ,一瓶 5L 装的该食用油质量是多少 kg?
一个质量为 117g 的铁球,体积为 20cm (ρ 铁 = 7.9g/cm ),判断该铁球是否为空心?若空心,空心部分体积多大?
课堂总结
密度计算的核心是灵活运用基本公式 ρ=m/V 及变形公式 m=ρV、V=m/ρ。
计算时必须保证单位统一,明确各物理量的单位换算关系。
解决实际问题时,需先分析已知条件,挖掘隐含信息(如体积相等、质量关系等),再选择合适公式计算。
通过密度计算可以解决物质鉴别、质量 / 体积估算、物体实心空心判断等问题,体现了密度知识在生活中的实用价值。
课后作业
一个长方体木块,长 5cm、宽 4cm、高 3cm,质量为 120g,求木块的密度。
修建一座桥需要用密度为 2.5×10 kg/m 的石料 500m ,这些石料的总质量是多少吨?
一个空瓶的质量为 200g,装满水后总质量为 700g,若装满某种液体后总质量为 600g,求该液体的密度。
查阅资料,找到你家所用防盗门的材质及密度,测量其长、宽、厚,估算防盗门的质量。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.密度的公式?
2.水的密度是多少?表示什么含义?
3.知道了密度公式中的任意两个,如何求第三个量?
复习与回顾
求质量
求体积
鉴别物质
一、密度公式应用
应用类型 应用公式 适用情境
求密度 ρ = 测物质密度、鉴别物质
求质量 m =ρV 求质量不易直接测量的物体的质量(如高大的石碑、油罐车中的油、成堆的粮食)
求体积 V = 求不便直接测量体积的物体的体积(如铜线的体积、不规则容器的容积等)
一、密度公式应用
1.某地有一水库,如图所示,已知它的最大容积为7.5×106m3,那么,这个水库最多可以积蓄多少吨水?
练一练
解:m=ρV=1.0×103kg/m3×7.5×106m3
=7.5×106kg
=7.5×106t
一、密度公式应用
例2:例某城市有一座大理石雕塑,如图所示,已知其质量为18.5t,它的体积是多少?
一、密度公式应用
物质名称 密度 物质名称 密度
锇 铝
金 大理石
铅 砖
银 冰
铜 蜡
钢、铁 干松木
一些固体的密度
二、学查密度表
一些液体的密度
物质名称 密度 物质名称 密度
水银 植物油
硫酸 煤油
海水 酒精
纯水 汽油
二、学查密度表
一些气体的密度(0℃ ,在标准大气压下)
物质名称 密度 物质名称 密度
二氧化碳 1.98 一氧化碳 1.25
氧 1.43 氦 0.18
空气 1.29 氢 0.09
二、学查密度表
1.一般:ρ固>ρ液>ρ气 ;
2.一些物质密度相同:如冰和蜡,酒精和煤油;
3.同种物质物态不同密度可能不同:如冰和水;
4.固体和液体密度用国际单位,数值都表示为“×103 ”的形式,如ρ水=1.0×103 kg/m3 ;气体密度用国际单位,数值没有“×103”,如 ρ空气=1.29 kg/m3。
观察表中数据能发现一些规律吗?
二、学查密度表
例1:如图所示,一枚第25届奥运会的纪念币,它的质量为16.1g,体积为1.8cm3。试求制成这种纪念币的金属的密度,并从密度表中找出它是那种金属。
已知:纪念币的质量m=16.1g=1.61×10-2kg,纪念币的体积V=1.8cm3=1.8×10-6m3。
求:制成纪念币的金属的密度ρ。
答:制成纪念币的金属的密度为8.9×103kg/m3。
查密度表可知纪念币是铜币
二、学查密度表
1.比例题
例1 甲、乙两种物质密度之比是3:2,质量之比是
2:1,求它们的体积之比。
三、密度计算应用
2.巧妙测量
例2 一只空瓶质量是0.2kg,装满水后总质量是1.0kg,倒掉水后再装满另一种液体,总质量是1.64kg,求这种液体的密度。
分析:该液体的密度要用它的质量与其体积之比求得,而其质量等于液体与瓶的总质量减去瓶的质量,其体积等于瓶的容积,也等于水的体积,水的体积等于水的质量除以水的密度,而水的质量又等于水和瓶的总质量减去瓶的质量。
三、密度计算应用
解题心得归纳:
解这类题时要抓住同一个瓶子装满不同的液体其容积不变。
三、密度计算应用
例3 为了测定某种小钢球的密度,先在一只空瓶中装满水,测得总质量是540g,然后将质量是97.5g的小钢球装入瓶内,溢出一部分水后,再测其总质量是625g,求这种小钢球的密度。
分析:因为题中已经给出了钢球的质量,要求钢球的密度,关键是求出小钢球的体积.小钢球的体积等于钢球排出的水的体积。只要求出钢球排出的水的质量,利用密度变形公式就可以求出水的体积。而排出的水的质量可以这样求:用原来满瓶水和瓶的总质量减去剩下的水和瓶的总质量即可。
三、密度计算应用
三、密度计算应用
例4 学校安装电路需用铜线,手头有一卷铜线,其质量为178kg,横截面积为2.5mm2,则这卷铜线有多长?
分析:要求铜线的长,则必须知道铜线的体积,然后根据V=SL求出长度。
三、密度计算应用
3.合金问题
例5 金、银合金的质量是530g,体积是35cm3,则金、银各有多少克?
分析
合金问题要抓住的思路。
三、密度计算应用
三、密度计算应用
例6 某实验室需要密度是1.1×103kg/m3 的盐水.现配制了0.5dm3的盐水,称得盐水的质量是0.6kg,这种盐水是否符合要求?若不符合要求,应该加盐还是加水?加多少?
分析:先求出盐水的密度,然后与标准盐水的密度进行比较,如果等于标准盐水密度,那么就符合要求。如果大于或小于标准盐水密度,就都不符合要求。若大于标准盐水密度,则应加水;若小于标准盐水密度,则应加盐。
三、密度计算应用
三、密度计算应用
5.选材问题
例9 一位飞机设计师,为减轻飞机的重力,要把一个钢制零件换成铝制零件,使其质量减少104kg,则这个零件共需铝多少千克?
分析:
钢制零件换成铝制零件其体积不变。
三、密度计算应用
三、密度计算应用
知识点1 密度公式的应用
1.母题 教材P133信息浏览 现代宇宙科学告诉我们,恒星在
演变过程中会形成密度很大的天体,如中子星、黑洞等。据
推测中子星的质量约为__________ ,则
中子星的密度约为__________ 。
返回
2.[2024·合肥蜀山区模拟]已知原来烧杯中盛有的酒精和烧
杯的总质量为 ,将部分酒精倒入量筒后,剩余的酒精与
烧杯的总质量如图甲所示,倒入量筒中的酒精的体积如图乙
所示,则可计算该酒精的密度为___________ 。
【点拨】图甲中剩余的酒精与烧杯的总质量
,量筒中酒精的质量
,由图乙可知,量筒的
分度值是,量筒中酒精的体积 ,酒
精的密度 。
返回
3.质量为的空瓶,装满水后的总质量为 ,瓶的容
积为_______。该瓶最多能装质量为 的某液体,此
液体的密度为__________。(水的密度为 )
1 500
【点拨】瓶子装满水后,水的质量
,瓶子的容积
,该瓶最多能装质量为
的某液体,此液体的密度
。
返回
4.过年小明收到了一份特殊的“压岁钱”——一两的银元宝。
小明给一个碗里装入适量水并测出总质量为 ,再将银元
宝浸没在水中,在水面处标上标记,测出总质量为 。将
银元宝从水中取出,再向碗里加水到标记处,测出总质量为
。银元宝的体积是___ ;银元宝的密度是_________
;所测的密度值______(填“偏大”“偏小”或“准确”)。
5
准确
【点拨】由题意得,将银元宝从水中取出,再向碗里加水,
所加水的体积即为银元宝的体积。所加水的质量
,银元宝的体积
; 据题知,银元宝的质量
,所以银元宝的密度
,虽然将银元
宝拿出时带走了一部分水,但是再补水至标记处时被带走的
水又会被补充回来,所以结果仍然准确。
返回
5.为了测饮料的密度,小军进行了如下操作:他找了一个玻
璃瓶,测出其质量为 ,将其盛满水测得总质量
为 ,然后把水倒干净,盛满饮料测得总质量为
。(水的密度为 )求:
(1)玻璃瓶的容积。
【解】玻璃瓶装满水后水的质量
,
由 可得,水的体积
,玻璃瓶的容积
。
(2)饮料的密度。
【解】饮料的质量
,
饮料的体积 ,
饮料的密度 。
(3)一个标有“ ”的塑料瓶,最多能盛多少千克这种饮料?
【解】一个标有“ ”的塑料瓶,最多能盛饮料的体积
,
最多盛饮料的质量
。
返回
知识点2 密度表与物质鉴别
6. [2024·北京西城区期中]下表是常温常压下部分物质的
密度值。根据表格中信息,下列说法正确的是( )
金 汞
铜 纯水
钢、铁 植物油
酒精
A. 固体的密度一定比液体的密度大
B. 体积相同的植物油和酒精,酒精的质量大
C. 质量相同的实心铜块和铁块,铁块的体积大
D. 不同物质的密度一定不同
√
【点拨】由表格数据可知,冰的密度小于纯水的密度,因此
固体的密度不一定比液体的密度大,故A错误;由表格数据
可知,植物油的密度大于酒精的密度,由 可知,体积
相同的植物油和酒精相比,植物油质量大,故B错误;由表
格数据可知,铜的密度大于铁的密度,由 可知,质量
相同的实心铜块和铁块相比,铁块的体积大,故C正确;由
表格数据可知,冰和植物油的密度相同,因此不同物质的密
度可能相同,故D错误。
返回
7.“摘星星”的妈妈王亚平从空间站回到地球,把自己从太空
摘的“星星”送给了女儿。若这枚来自太空的实心星星纪念币
的质量为,体积为 ,则这枚纪念币的密度是
__________ ,______(填“是”或“不是”)纯金制成
的。
不是
【点拨】根据 得,纪念币的密度
,已知
, ,故该纪念币不是用纯金制
成的。
返回
纠易错 不能正确计算混合物体的密度
8. 由质量相等的甲、乙两种金属制成合金块,两种金属的密
度分别为和 ,若总体积不变,则合金块的密度为( )
C
A. B. C. D.
【点拨】设甲、乙两金属的质量均为 ,则两金属的体积分
别为, ,合金块的密度
。
返回
9. 如图所示,天平已调平,将4个相同的甲球和5个相同的乙
球按图示摆放至天平左右两盘时,天平仍平衡,已知甲球和
乙球的体积相同,下列说法正确的是( )
D
(第9题)
A. 1个甲球与1个乙球的质量之比为
B. 3个甲球与4个乙球的质量之比为
C. 甲球与乙球的密度之比为
D. 甲球与乙球的密度之比为
(第9题)
【点拨】由题意和图示可得,
,整理可得
,即1个甲球与1个乙球
的质量之比为 ,故A错误;3个甲球
与4个乙球的质量之比为 ,
故B错误;已知,由 可得,甲、乙两球的密度
之比 ,故C错误,D正确。
返回
(第10题)
10.[2025·合肥专题练习]某医院 重症
监护室内配有充满氧气的钢瓶,其总质量
为,瓶内氧气的密度为;使用 后,
总质量变为 ,瓶内氧气的密度变为
; 再使用一段时间后,总质量变为
20
,则此时瓶内氧气的密度为_____,氧气瓶的质量是
____ 。如图所示为某物质的密度与体积的关系,则阴影部
分的面积 表示的物理量的值为_____。
(第10题)
【点拨】设氧气瓶的质量为 ,其容积为
,则由 可得,刚启用时瓶内氧气的
密度 ,使用1小时,总质量
变为 ,而氧气的体积不变(等于氧气
瓶的容积),此时瓶内氧气的密度为
, 解得氧气瓶的质量
,总质量为 的氧气瓶,最
初氧气的质量为 ,再
使用一段时间,总质量变为 ,则此时
瓶内氧气的质量为 ,
氧气的体积一定,根据 可知,氧气的
密度和氧气的质量成正比,所以,此时瓶
(第10题)
内的氧气密度应为原来的,应为 。
分析图像中的横坐标和纵坐标可知,横坐
标表示体积,纵坐标表示密度,故此时阴
影部分的面积 ,即为该物质的质量,
则 。
(第10题)
返回
11.[2025·盐城期末]走到刚下的积雪上面,感觉很松软。
小宇用一个带有刻度的容器收集了 积雪,用电子秤
测得该容器装雪前后质量之差为 。问:
(1)小宇采集的积雪的密度是多少克每立方厘米?
【解】积雪密度 。
(2)若组成雪花的冰晶密度为 ,则小宇采集的积
雪中,空心的体积占了多少?(用百分比表示)
【解】组成雪花的冰晶的体积 ,
空心的体积 ,
空心的体积占比为 。
(3)查阅资料发现,降雪量是指将雪熔化后,以毫米为计
量单位的水的深度。小宇测出地面上积雪平均厚度为 ,
则本次降雪量大小是多少?
【解】雪熔化前后质量不变,有,由 得,
,则 ,
,代入得
,解得
。
返回
密度知识的应用
密度表
密度知识的应用
固体、液体、气体的密度
比例题
巧妙测量
冰和水的问题
合金问题
选材问题
用密度知识解释生活中的常见现象
课堂小结
谢谢观看!
同课章节目录
