6.2物质的密度--2025-2026学年教科版八年级上册物理教学课件(54页PPT)
文档属性
| 名称 | 6.2物质的密度--2025-2026学年教科版八年级上册物理教学课件(54页PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-14 06:44:41 | ||
图片预览








文档简介
(共54张PPT)
6.2物质的密度
第6章 质量与密度
教科版2025-2026学年 物理八年级上册【精做课件】
授课教师:********
班 级:********
时 间:********
6.2 物质的密度
学习目标
理解密度的概念,知道密度是物质的一种特性,能说出密度的物理意义。
掌握密度的公式和单位,能进行密度单位的换算,会用密度公式进行简单的计算。
学会用天平和量筒(或量杯)测量固体和液体的密度,能正确记录实验数据并进行计算。
了解常见物质的密度,知道密度在生活、生产和科学研究中的应用。
通过实验探究,培养实验操作能力、数据分析能力和归纳总结能力,体会科学探究的方法。
情境导入
展示一组图片:体积相同的铁块和木块、大小不同的两块铁块、同样是水但体积不同的两杯水。
提问:体积相同的铁块和木块,质量不同;大小不同的两块铁块,质量不同,但它们的质量与体积的比值是否相同?同样是水,不同体积的水质量不同,质量与体积的比值又是否相同?
引出主题:这些问题都与物质的密度有关,本节课我们就来学习物质的密度。
密度的概念
探究实验:比较相同体积不同物质的质铜
8.9×10
煤油
0.8×10
铅
11.3×10
水银
13.6×10
空气
1.29
说明:
气体的密度在通常情况下是指在标准大气压下的密度。
密度表中的数据可以帮助我们了解不同物质的密度大小,在需要时进行查询和应用。
密度的测量
测量原理
根据密度公式 ρ = m/V,只要测出物体的质量 m 和体积 V,就可以计算出物质的密度。
测量工具
测量质量:天平。
测量体积:
形状规则的固体(如正方体、长方体、圆柱体):用刻度尺测量其边长、直径等,根据体积公式计算体积。
形状不规则的固体和液体:用量筒或量杯测量体积。
量筒(或量杯)的使用
构造:量筒(或量杯)是测量液体体积的仪器,上面标有刻度和单位(通常是 mL,1mL = 1cm )。量筒的刻度是均匀的,量杯的刻度是上密下疏的。
使用方法:
量筒(或量杯)要放在水平台上。
读数时,视线要与量筒(或量杯)内液体的凹液面的底部相平(如果是凸液面,如水银,则视线要与凸液面的顶部相平)。
注意事项:
不能用量筒(或量杯)加热或量取过热的液体。
不能用量筒(或量杯)溶解物质或进行化学反应。
读数时,若俯视读数,会使读数偏大;若仰视读数,会使读数偏小。
测量固体的密度(以形状不规则的石块为例)
实验目的:测量形状不规则石块的密度。
实验器材:天平、砝码盒、石块、量筒、水、细线。
实验步骤:
用天平测出石块的质量 m,并记录。
在量筒中倒入适量的水,记下此时水的体积 V 。
用细线系住石块,将石块缓慢放入量筒中,使石块完全浸没在水中,记下此时水和石块的总体积 V 。
计算石块的体积 V = V - V 。
根据密度公式计算石块的密度 ρ = m/V。
数据记录与计算:
石块的质量 m/g
水的体积 V /cm
水和石块的总体积 V /cm
石块的体积 V/cm
石块的密度 ρ/(g cm )
25
50
60
10
2.5
注意事项:
石块要完全浸没在水中,但不能碰到量筒的底部或壁。
倒入量筒中的水要适量,既要能浸没石块,又要在石块放入后不超过量筒的量程。
测量液体的密度(以水为例)
实验目的:测量水的密度。
实验器材:天平、砝码盒、烧杯、水、量筒。
实验步骤:
用天平测出烧杯和水的总质量 m ,并记录。
将烧杯中的一部分水倒入量筒中,记下量筒中水的体积 V。
用天平测出烧杯和剩余水的总质量 m ,并记录。
计算量筒中水的质量 m = m - m 。
根据密度公式计算水的密度 ρ = m/V。
数据记录与计算:
烧杯和水的总质量 m /g
量筒中水的体积 V/cm
烧杯和剩余水的总质量 m /g
量筒中水的质量 m/g
水的密度 ρ/(g cm )
150
100
50
100
1.0
注意事项:
向量筒中倒水时,要小心操作,避免水洒出。
读数时,量筒要放在水平台上,视线要与凹液面底部相平。
密度的应用
鉴别物质:每种物质都有自己的密度,通过测量物质的密度,可以鉴别物质的种类。例如,通过测量未知金属块的密度,与密度表中的数据对比,可以判断该金属块是什么金属。
计算不便于直接测量的质量:对于质量很大或形状不规则不便于直接用天平测量的物体,若知道其密度和体积,可以根据 m = ρV 计算出物体的质量。例如,计算一大块大理石的质量,先测量其体积,再查出大理石的密度,就可以算出质量。
计算不便于直接测量的体积:对于形状不规则或体积很小不便于直接用量筒测量的物体,若知道其密度和质量,可以根据 V = m/ρ 计算出物体的体积。例如,计算一枚戒指的体积,用天平测出其质量,查出金的密度(假设是金戒指),就可以算出体积。
选择材料:在生产中,根据不同的需求选择密度合适的材料。例如,制造飞机时,为了减轻飞机的质量,常选用密度小的铝合金材料;制造铅球时,为了使铅球有较大的质量,选用密度大的铅作为材料。
判断物体是否空心:对于由某种物质制成的物体,通过测量其密度,并与该物质的密度对比,若测量的密度小于物质的密度,则该物体是空心的。例如,一个铝球,测量出其密度小于铝的密度(2.7g/cm ),则该铝球是空心的。
课堂活动:探究同种物质的密度是否与质量、体积有关
活动任务:小组合作,选用同种物质(如不同体积的铁块或不同体积的水)进行实验,探究同种物质的密度是否与质量、体积有关。
实验器材:天平、砝码盒、不同体积的铁块(或不同体积的水)、量筒。
实验步骤:
对于铁块:用天平分别测出不同体积铁块的质量,用刻度尺或量筒测量出它们的体积,计算出质量与体积的比值(密度),比较比值是否相同。
对于水:用量筒量取不同体积的水,用天平测出它们的质量,计算出质量与体积的比值(密度),比较比值是否相同。
数据分析与结论:分析实验数据,发现同种物质不同质量、体积的情况下,质量与体积的比值(密度)基本相同,得出结论:同种物质的密度与质量、体积无关。
密度的计算
基本公式应用:
已知质量和体积,求密度:ρ = m/V。
已知密度和体积,求质量:m = ρV。
已知密度和质量,求体积:V = m/ρ。
单位换算示例:
铁的密度是 7.9×10 kg/m = 7.9g/cm 。
酒精的密度是 0.8g/cm = 0.8×10 kg/m 。
计算示例:
一块体积为 20cm 的铁块,质量是多少?(铁的密度是 7.9g/cm )
解:根据 m = ρV,可得 m = 7.9g/cm ×20cm = 158g。
一个质量为 500g 的瓶子,装满水后总质量为 1500g,求瓶子的容积。(水的密度是 1g/cm )
解:水的质量 m = 1500g - 500g = 1000g,根据 V = m/ρ,可得瓶子的容积 V = 1000g/1g/cm = 1000cm 。
随堂练习
某种物质组成的物体的______与它的______之比叫做这种物质的密度,密度的公式是______,国际单位是______。
水的密度是______kg/m ,它表示的物理意义是______。
体积为 1m 的冰块全部熔化成水后,水的质量是______kg,水的体积是______m 。(冰的密度是 0.9×10 kg/m )
一个铝块的质量是 54g,体积是 20cm ,则铝的密度是______g/cm ,合______kg/m 。
用天平和量筒测量某石块的密度,测得石块的质量为 50g,量筒中水的体积为 30cm ,放入石块后水和石块的总体积为 40cm ,则石块的密度是多少?
答案
质量;体积;ρ = m/V;kg/m
1.0×10 ;1 立方米水的质量是 1.0×10 千克
900;0.9
2.7;2.7×10
解:石块的体积 V = 40cm - 30cm = 10cm ,石块的密度 ρ = m/V = 50g/10cm = 5g/cm 。
总结
密度是物质的一种特性,定义为质量与体积之比,公式为 ρ = m/V,单位有 kg/m 和 g/cm ,两者的换算关系是 1g/cm = 1×10 kg/m 。
同种物质的密度与质量、体积无关,不同物质的密度一般不同,同种物质的密度还与状态有关。
测量物质的密度需要测量质量和体积,质量用天平测量,体积根据物体的形状选择合适的工具测量(刻度尺或量筒)。
密度在鉴别物质、计算质量或体积、选择材料等方面有广泛的应用。
通过实验探究和计算练习,掌握了密度的概念、测量方法和应用,提高了实验操作和数据分析能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.问题探究:不同物体的质量大小
问题 结果 归纳总结
体积相同的铝 块,质量一样吗 通过天平称量 发现质量一样 (1)体积相同的同
种物质,质量相同;
(2)体积不同的同
种物质,质量不同;
(3)体积相同的不
同物质,质量一般不
同
体积不同的铁 块,质量一样吗 通过天平称量 发现质量不一 样 问题 结果 归纳总结
体积相同的铝块 和铁块,质量一 样吗 通过天平称量 发现质量不一 样 (1)体积相同的同
种物质,质量相同;
(2)体积不同的同
种物质,质量不同;
(3)体积相同的不
同物质,质量一般不
同
2.实验探究:物体的质量与体积的关系
实验设计 选取不同体积的长方体组(如铝块、铁块、铜
块),测出其质量和体积,分别计算出单位体
积的质量,并进行比较
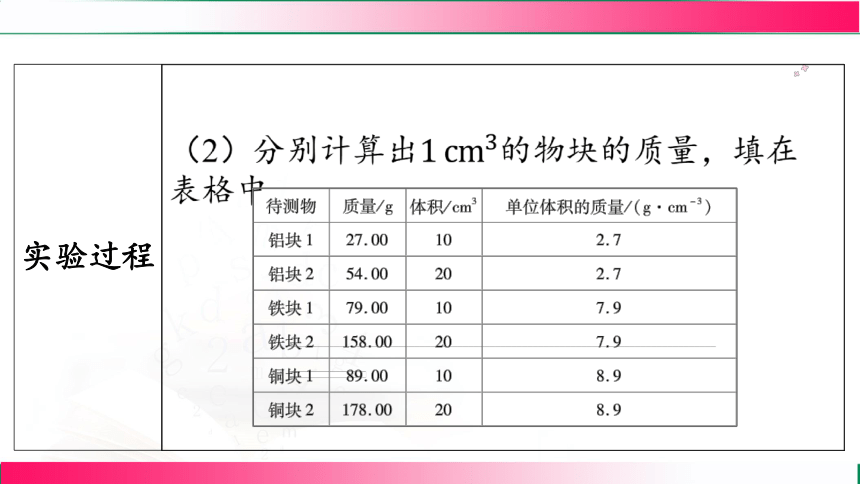
实验过程 (1)分别用电子天平测量长方体组中大小不
同的物块的质量,用刻度尺测量其尺寸并计算
其体积,填写在下面的表格中;
实验过程
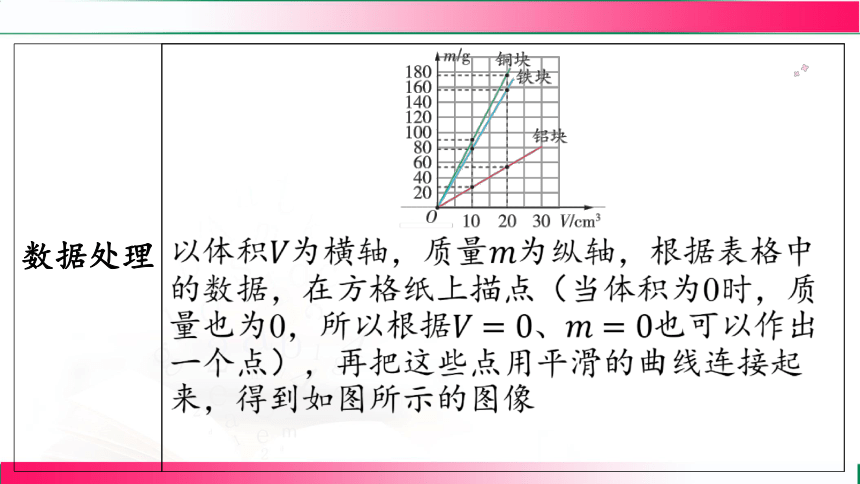
数据处理
实验结论 (1)分析表中数据可知:
①物块的体积增大为原来的几倍,其质量也增
大为原来的几倍,质量与体积之比不变.
②铝块、铁块、铜块的质量与其体积的比值不
同,即不同物质组成的物体,其质量与体积的
比值一般不同.
(2)分析图像可知:铝块、铁块、铜块的图
像都是一条过原点的倾斜直线,即同种物质组
成的物体,其质量与体积成正比
交流讨论 “质量与体积的比值”就是“单位体积的质量”,
同种物质的质量与其体积的比值是一定的,即
物体的质量与其体积的比值反映了物质的一种
特性
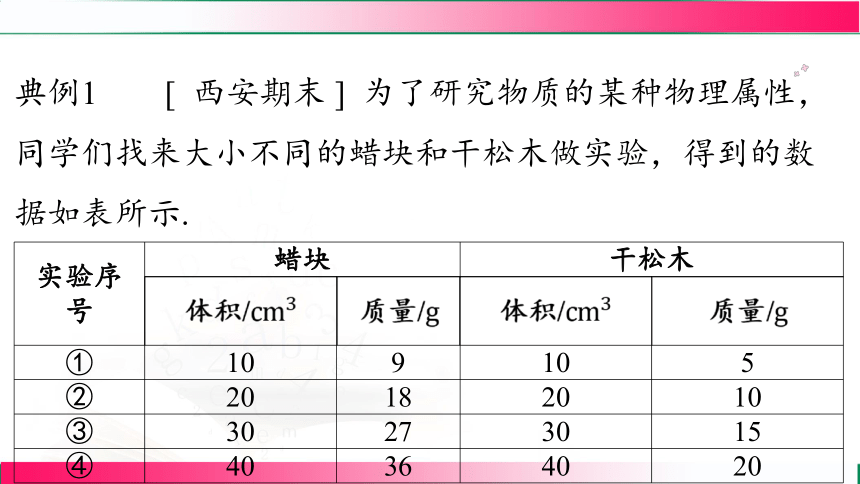
典例1 [ 西安期末 ] 为了研究物质的某种物理属性,
同学们找来大小不同的蜡块和干松木做实验,得到的数
据如表所示.
实验序 号 蜡块 干松木
① 10 9 10 5
② 20 18 20 10
③ 30 27 30 15
④ 40 36 40 20
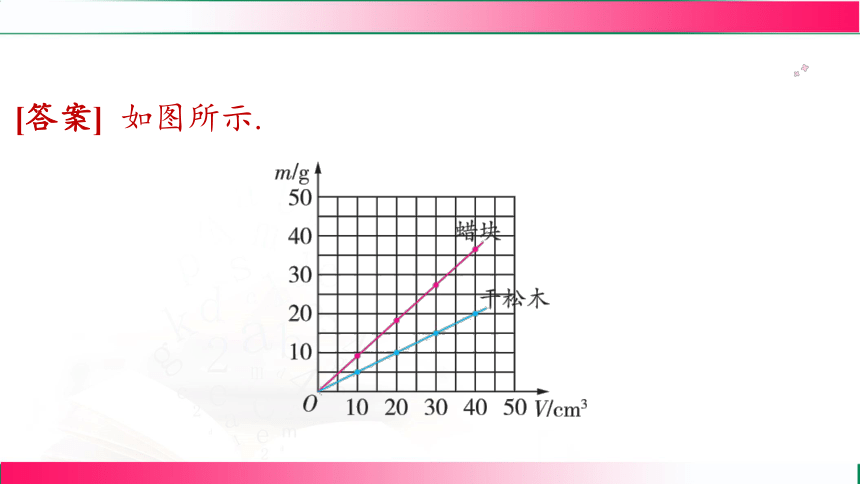
(1)在如图的方格纸中,用图线分
别把蜡块和干松木的质量随体积变化
的情况表示出来.
[答案] 如图所示.
[解析] 根据表中蜡块和干松木的体积和质量数据在方格
纸上描点,并用平滑的线进行连接.
(2)通过对比数据和分析图像, 可以得到:
结论1:同种物质,质量与体积的比值是______(选填“相等”
或“不相等”)的.
结论2:不同物质,质量与体积的比值是________
(选填“相等”或“不相等”)的.
相等
不相等
(3)由以上分析可知, 若测得另一干松木的质量为 ,
则它的体积应为____ .
80
[解析] 同种物质组成的物体,其质量与体积的比值相等,
由此可知,,解得 .
3.密度的概念
在物理学中,某种物质组成的物体的质量与其体积之比
叫作这种物质的密度,用符号 表示.
4.对密度概念的理解
(1)密度是物质的一种特性,在条件一定的情况下,每
种物质的密度是确定的.密度不随物体质量或体积的变化
而变化.
(2)不同物质的密度一般不同.
特别提醒
日常生活中,人们往往感觉密度大的物质“重”,密度小的
物质“轻”,比如,常说的“铁比棉花重”,实质上是指铁的
密度大于棉花的密度,真正的重或轻取决于物体的质量.
5.密度公式及单位
(1)密度公式: .变形公式:,.
(2)密度的单位
①国际单位: ,读作“千克每立方米”.
②常用单位: ,读作“克每立方厘米”.
.
换算过程: .
特别提醒
运用密度公式时的注意事项
(1)公式 是密度的定义式,适用于所有物体
(包括气体、液体和固体)密度的计算.
(2)质量、体积和密度必须对应同一物态的同一物体.
(3)单位统一,对应使用如下:
①质量单位用,体积单位用,则密度单位为 ;
②质量单位用,体积单位用,则密度单位为 .
教材深挖
物质密度的特点及规律
(1)密度表中固体、液体的密度标有常温、常压,气体
的密度标有 、一个标准大气压,这说明密度与温度、
压强等有关.
(2)一般情况下, ;常见液体中,水银的
密度最大(大于大多数固体的密度);常见金属中,铝
的密度最小;常见气体中,氢气的密度最小.
(3)同种物质的物态不同,其密度不同.当物质在不同物
态间转化时,其质量不变,但体积发生变化,密度也发
生改变.如常温常压下,水的密度为 ,变
为冰后密度为 ,密度变小,体积变大.
(4)不同种物质的密度可能相同,如冰和蜡的密度相同,
煤油和酒精的密度相同.
典例2 如图,放在一朵花上的
“全碳气凝胶”是我国科学家研制的迄今为止密
度最小的材料,密度只有 .某汽
3.2
车发动机采用密度为 的高强度合金材料制
造,质量为 ;若采用“全碳气凝胶”制造,需要“全
碳气凝胶”的质量为____ .
[解析] 由 可得发动机的体积为
,若采用“全碳气凝胶”制
造, ,则需要“全碳气凝
胶”的质量为
.
1.利用密度知识可以鉴别物质类别
根据密度公式,把测得的物体的质量和体积代入即可求
出物质的密度,再从密度表中查出该密度的物质,二者
对比即可以进行物质的鉴别.
此方法为粗略鉴别,若想准确鉴别,还需要配合
其他方法.
2.密度在生产生活中的应用
(1)根据密度大小选择合适的材料(物质).为了减轻车
辆、飞机的自重,常选择密度较小的合金材料或复合材
料;产品包装则应选择密度较小的泡沫塑料等.
(2)根据密度,鉴别优劣.酒、牛奶等物质,其产品质量
的好坏和密度有关,因此其密度是质检的重要参数.农业
中还可以用盐水来选种,饱满健壮的种子在水中会因为
密度大而下降,干瘪的种子会浮在水面上.
(3)测量密度,确定矿藏种类.勘探队员通过采集样品的
密度等信息,确定矿藏种类及其经济价值.
典例3 一棱长为 的正方体实心金属块,其质量为
.该金属块是由下表中的某一金属物质组成的,则组
成该金属块的物质是( )
常温下一些金属的密度/
金 19.3 铝 2.7
银 10.5 铁 7.9
C
A.金 B.银 C.铝 D.铁
[解析] 该金属的密度
,因此该金
属是铝.
知识点1 认识密度
1. [2023·海南]下列现象中,密度变大的是( B )
A. 铁棒磨成针
B. 冰熔化成水
C. 橡皮泥捏成小船
D. 氧气瓶内的氧气用了一段时间
B
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 密度公式因能被写成如图所示的样式,而被称为“物理最
美公式”,下列关于密度的说法正确的是( B )
A. 铁比铝“重”,“重”指的是铁的质量比铝的质量大
B. 一罐氧气用掉部分后,罐内氧气的质量变
小,密度变小
C. 一块砖被切成体积相等的两块后,砖的密度变为原来的一半
D. 利用铝合金材料制作列车车体,因为它的密度大,行驶时列车更稳
B
1
2
3
4
5
6
7
8
9
10
11
12
13
知识点2 密度的计算
3. [2024·济南模拟]加气混凝土砌块是一种轻质多孔、防火性
能良好、具有一定抗震能力的新型建筑材料,还具有环保
等优点,被广泛使用于高层框架结构建筑中。现有一块加
气混凝土砌块,其体积为1.08×104 cm3,质量为6.48 kg。该加气混凝土砌块的密度为 。
0.6×103 kg/m3(或0.6 g/cm3)
1
2
3
4
5
6
7
8
9
10
11
12
13
4. 某AD钙奶的密度为1.05×103 kg/m3,其物理含义是
。
它的包装盒上标注了净含量450 mL,瓶中所装AD钙奶的
质量为 g。将此瓶AD钙奶喝掉一半以后,剩余
AD钙奶的密度将 (填“变大”“变小”或“不
变”)。
每
立方米AD钙奶的质量是1.05×103 kg
472.5
不变
1
2
3
4
5
6
7
8
9
10
11
12
13
【点拨】
AD钙奶的密度ρ=1.05×103 kg/m3,它表示的物理含义是每立方米AD钙奶的质量是1.05×103 kg;它的包装盒上标注了净含量V=450 mL=450 cm3,根据密度公式得,瓶中所装AD钙奶的质量m=ρV=1.05 g/cm3×450 cm3=472.5 g;喝掉一半后,其密度不变。
1
2
3
4
5
6
7
8
9
10
11
12
13
5. 如图所示是小明在探究甲、乙两种不同液体的质量与体积
的关系时得出的图像,由图像可知,甲、乙两种液体的密
度之比为 ,其中乙的密度为 kg/m3,
一只瓶子刚好能装下1 kg的液体甲,
则这只瓶子 (填“能”或
“不能”)装下1 kg的液体乙。
4∶1
0.5×103
不能
(第5题)
1
2
3
4
5
6
7
8
9
10
11
12
13
【点拨】
由图像可知,当体积V=4 cm3时,对应的质量m甲=
8.0 g、m乙=2.0 g,由ρ=可得,甲、乙两种液体的密度之比ρ甲∶ρ乙=∶=m甲∶m乙=8.0 g∶2.0 g=4∶1;其中乙的密度ρ乙===0.5 g/cm3=0.5×103 kg/m3;由ρ=可得V=,质量相同时,密度小的体积大,一只瓶子刚好能装下1 kg的液体甲,则这只瓶子不能装下1 kg的液体乙。
1
2
3
4
5
6
7
8
9
10
11
12
13
知识点3 密度的应用
6. [现代科技]中国海上巨型风机——巨无霸SL5000是史上最
大的单体风力发电机,如图所示,它的每个叶片长62 m,
它转动起来能够扫过将近两个足球场大的面积。为了让风
更易带动起扇叶,制成叶片的材料应该具有( C )
A. 较大的质量 B. 较低的熔点
C. 尽量小的密度 D. 较好的吸热性
(第6题)
C
1
2
3
4
5
6
7
8
9
10
11
12
13
7. [传统文化]山西绛州澄泥砚,始创于唐代,是中国“四大
名砚”之一。如图所示是绛州澄泥砚传承人蔺涛正在利用
汾河下游的澄泥雕刻砚台的场景,雕刻过程中不发生变化
的是( B )
B
A. 澄泥的质量
B. 澄泥的密度
C. 澄泥的体积
D. 澄泥的形状
1
2
3
4
5
6
7
8
9
10
11
12
13
8. [2024·西安开学]如表是部分物质在0 ℃、标准大气压下的
密度表,小刚由此提出了对密度的一些看法,你认为正确
的是( D )
0 ℃、标准大气压下部分物质的密度/(kg/m3) 水 1.0×103 冰 0.9×103
水银 13.6×103 干松木 0.5×103
酒精 0.8×103 铜 8.9×103
煤油 0.8×103 铝 2.7×103
1
2
3
4
5
6
7
8
9
10
11
12
13
A. 固态物质的密度一定比液态物质的密度大
B. 同种物质的密度一定相同
C. 质量相同的水银和酒精,水银体积较大
D. 体积相同的实心铜块和铝块,铜块的质量大
1
2
3
4
5
6
7
8
9
10
11
12
13
固态物质干松木的密度小于液态物质水的密度,A错
误;水和冰是同种物质,但密度不同,B错误;质量相同
的水银和酒精,因为ρ水银>ρ酒精,由V=可知,水银的体
积较小,C错误;体积相同的实心铜块和铝块,因为m=
ρV,ρ铜>ρ铝,所以铜块的质量大,D正确。
【答案】D
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
9. [2024·泰州月考]野战部队携带的压缩饼干与普通饼干相
比,好处在于质量相等的情况下,它的密度 (填
“较大”或“较小”,下同),体积 。如图所
示,点燃蜡烛会使上方的扇叶旋转起来,这是因为蜡烛的
火焰使附近空气的温度升高,体积膨胀,空气的密度
(填“变大”或“变小”),所以热空气
(填“上升”或“下降”)形成气流,
气流流过扇叶时,带动扇叶转起来。
较大
较小
变
小
上升
1
2
3
4
5
6
7
8
9
10
11
12
13
【点拨】
压缩饼干与普通饼干相比,好处是在质量相等的情况下,物质间隙较小,所以体积较小,由ρ=可知,质量相等的情况下,它的密度较大。点燃蜡烛,附近的空气吸收热量,温度升高,体积膨胀,密度变小,密度小的热空气上升,形成对流,使扇叶转动。
1
2
3
4
5
6
7
8
9
10
11
12
13
10. [2024·高新一中期中]甲、乙两个实心金属块,它们的体
积之比为5∶4,将它们分别放在已调平的天平左右盘中,
天平恰好平衡,则甲和乙的质量之比为 ,密度之
比为 ;若将甲切去五分之二,将乙切去四分之
三,那么甲和乙剩余部分的密度之比是 ,甲和乙
剩余部分的质量之比是 。某医院急诊室的氧气
瓶中,氧气的密度为6 kg/m3,给急救病人供氧用去了氧
气质量的三分之一,则瓶内剩余氧气的密度为 . kg/m3。
1∶1
4∶5
4∶5
12∶5
4
1
2
3
4
5
6
7
8
9
10
11
12
13
【点拨】
天平平衡,说明两物体质量相同,所以甲和乙的质量之比为1∶1,密度之比===;因为密度是物质的一种特性,与物质的质量、体积的大小无关,所以切去一部分后,密度之比不变,仍为4∶5,因将甲切去五分之二,将乙切去四分之三,则甲和乙剩余部分的质量之比===12∶5。
1
2
3
4
5
6
7
8
9
10
11
12
13
原来氧气的密度为6 kg/m3,给急救病人供氧用去了氧气质量
的,氧气质量变为原来的,而氧气的体积保持不变(等于氧
气瓶的容积),根据ρ=可知,氧气的密度变为原来的,则
瓶内剩余氧气的密度ρ'=ρ=×6 kg/m3=4 kg/m3。
1
2
3
4
5
6
7
8
9
10
11
12
13
11. [2023·济宁]在测定某液体密度时,小明做了两次实验并
做了如下记录,则液体的密度ρ= g/cm3,容器的质
量m= g。
次数 液体的体积V/cm3 容器和液体的总质量m/g
1 58 79
2 107 128
1
21
1
2
3
4
5
6
7
8
9
10
11
12
13
【点拨】
由题意知,两次实验液体的质量之差Δm=128 g-79 g=49 g,液体体积之差ΔV=107 cm3-58 cm3=49 cm3,液体的密度ρ===1 g/cm3,由ρ=得,第一次实验时液体的质量m1=ρV1=1 g/cm3×58 cm3=58 g,容器的质量m=m总1-m1=79 g-58 g=21 g。
1
2
3
4
5
6
7
8
9
10
11
12
13
12. [2024·盐城月考]中国的粮食安全有保障,已连续多年增
产,但我们仍然要厉行节约。如图所示,小华家的晒谷
场上有一堆稻谷,体积为5 m3。为了估测这堆稻谷的质
量,他用一只空桶平平地装满一桶稻谷,测得桶中稻谷
的质量为9.9 kg;再用这只桶装满水,测得桶中水的质
量为9 kg。(ρ水=1.0×103 kg/m3)求:
1
2
3
4
5
6
7
8
9
10
11
12
13
【解】根据ρ=可得,桶中的水的体积
V水===9×10-3 m3。
(1)装满水时,桶中水的体积。
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)稻谷的密度。
【解】桶中稻谷的体积V0=V水=9×10-3 m3,
稻谷的密度ρ===1.1×103 kg/m3。
(3)这堆稻谷的总质量。
【解】这堆稻谷的总质量m总=ρV总=1.1×103 kg/m3× 5 m3=5.5×103 kg。
1
2
3
4
5
6
7
8
9
10
11
12
13
13. [科学推理]如图甲所示,A组是由材料、大小和厚度均相
同的小正四棱柱整齐叠加在一起的一个大正四棱柱(忽略
中间的缝隙),其底面积为100 cm2;B组是由另一种材料
制成的正四棱柱,其密度为0.75×103 kg/m3。现从A组
上逐块取下小正四棱柱并叠放在B组正四棱柱上,A、B
两组正四棱柱的质量随A组大正四棱柱减小的高度h的变
化关系图像如图乙所示,由图像可知,A组小正四棱柱
的密度为 kg/m3,B组正四棱柱的体积
为 m3。
0.8×103
1.28×103
1
2
3
4
5
6
7
8
9
10
11
12
13
谢谢观看!
6.2物质的密度
第6章 质量与密度
教科版2025-2026学年 物理八年级上册【精做课件】
授课教师:********
班 级:********
时 间:********
6.2 物质的密度
学习目标
理解密度的概念,知道密度是物质的一种特性,能说出密度的物理意义。
掌握密度的公式和单位,能进行密度单位的换算,会用密度公式进行简单的计算。
学会用天平和量筒(或量杯)测量固体和液体的密度,能正确记录实验数据并进行计算。
了解常见物质的密度,知道密度在生活、生产和科学研究中的应用。
通过实验探究,培养实验操作能力、数据分析能力和归纳总结能力,体会科学探究的方法。
情境导入
展示一组图片:体积相同的铁块和木块、大小不同的两块铁块、同样是水但体积不同的两杯水。
提问:体积相同的铁块和木块,质量不同;大小不同的两块铁块,质量不同,但它们的质量与体积的比值是否相同?同样是水,不同体积的水质量不同,质量与体积的比值又是否相同?
引出主题:这些问题都与物质的密度有关,本节课我们就来学习物质的密度。
密度的概念
探究实验:比较相同体积不同物质的质铜
8.9×10
煤油
0.8×10
铅
11.3×10
水银
13.6×10
空气
1.29
说明:
气体的密度在通常情况下是指在标准大气压下的密度。
密度表中的数据可以帮助我们了解不同物质的密度大小,在需要时进行查询和应用。
密度的测量
测量原理
根据密度公式 ρ = m/V,只要测出物体的质量 m 和体积 V,就可以计算出物质的密度。
测量工具
测量质量:天平。
测量体积:
形状规则的固体(如正方体、长方体、圆柱体):用刻度尺测量其边长、直径等,根据体积公式计算体积。
形状不规则的固体和液体:用量筒或量杯测量体积。
量筒(或量杯)的使用
构造:量筒(或量杯)是测量液体体积的仪器,上面标有刻度和单位(通常是 mL,1mL = 1cm )。量筒的刻度是均匀的,量杯的刻度是上密下疏的。
使用方法:
量筒(或量杯)要放在水平台上。
读数时,视线要与量筒(或量杯)内液体的凹液面的底部相平(如果是凸液面,如水银,则视线要与凸液面的顶部相平)。
注意事项:
不能用量筒(或量杯)加热或量取过热的液体。
不能用量筒(或量杯)溶解物质或进行化学反应。
读数时,若俯视读数,会使读数偏大;若仰视读数,会使读数偏小。
测量固体的密度(以形状不规则的石块为例)
实验目的:测量形状不规则石块的密度。
实验器材:天平、砝码盒、石块、量筒、水、细线。
实验步骤:
用天平测出石块的质量 m,并记录。
在量筒中倒入适量的水,记下此时水的体积 V 。
用细线系住石块,将石块缓慢放入量筒中,使石块完全浸没在水中,记下此时水和石块的总体积 V 。
计算石块的体积 V = V - V 。
根据密度公式计算石块的密度 ρ = m/V。
数据记录与计算:
石块的质量 m/g
水的体积 V /cm
水和石块的总体积 V /cm
石块的体积 V/cm
石块的密度 ρ/(g cm )
25
50
60
10
2.5
注意事项:
石块要完全浸没在水中,但不能碰到量筒的底部或壁。
倒入量筒中的水要适量,既要能浸没石块,又要在石块放入后不超过量筒的量程。
测量液体的密度(以水为例)
实验目的:测量水的密度。
实验器材:天平、砝码盒、烧杯、水、量筒。
实验步骤:
用天平测出烧杯和水的总质量 m ,并记录。
将烧杯中的一部分水倒入量筒中,记下量筒中水的体积 V。
用天平测出烧杯和剩余水的总质量 m ,并记录。
计算量筒中水的质量 m = m - m 。
根据密度公式计算水的密度 ρ = m/V。
数据记录与计算:
烧杯和水的总质量 m /g
量筒中水的体积 V/cm
烧杯和剩余水的总质量 m /g
量筒中水的质量 m/g
水的密度 ρ/(g cm )
150
100
50
100
1.0
注意事项:
向量筒中倒水时,要小心操作,避免水洒出。
读数时,量筒要放在水平台上,视线要与凹液面底部相平。
密度的应用
鉴别物质:每种物质都有自己的密度,通过测量物质的密度,可以鉴别物质的种类。例如,通过测量未知金属块的密度,与密度表中的数据对比,可以判断该金属块是什么金属。
计算不便于直接测量的质量:对于质量很大或形状不规则不便于直接用天平测量的物体,若知道其密度和体积,可以根据 m = ρV 计算出物体的质量。例如,计算一大块大理石的质量,先测量其体积,再查出大理石的密度,就可以算出质量。
计算不便于直接测量的体积:对于形状不规则或体积很小不便于直接用量筒测量的物体,若知道其密度和质量,可以根据 V = m/ρ 计算出物体的体积。例如,计算一枚戒指的体积,用天平测出其质量,查出金的密度(假设是金戒指),就可以算出体积。
选择材料:在生产中,根据不同的需求选择密度合适的材料。例如,制造飞机时,为了减轻飞机的质量,常选用密度小的铝合金材料;制造铅球时,为了使铅球有较大的质量,选用密度大的铅作为材料。
判断物体是否空心:对于由某种物质制成的物体,通过测量其密度,并与该物质的密度对比,若测量的密度小于物质的密度,则该物体是空心的。例如,一个铝球,测量出其密度小于铝的密度(2.7g/cm ),则该铝球是空心的。
课堂活动:探究同种物质的密度是否与质量、体积有关
活动任务:小组合作,选用同种物质(如不同体积的铁块或不同体积的水)进行实验,探究同种物质的密度是否与质量、体积有关。
实验器材:天平、砝码盒、不同体积的铁块(或不同体积的水)、量筒。
实验步骤:
对于铁块:用天平分别测出不同体积铁块的质量,用刻度尺或量筒测量出它们的体积,计算出质量与体积的比值(密度),比较比值是否相同。
对于水:用量筒量取不同体积的水,用天平测出它们的质量,计算出质量与体积的比值(密度),比较比值是否相同。
数据分析与结论:分析实验数据,发现同种物质不同质量、体积的情况下,质量与体积的比值(密度)基本相同,得出结论:同种物质的密度与质量、体积无关。
密度的计算
基本公式应用:
已知质量和体积,求密度:ρ = m/V。
已知密度和体积,求质量:m = ρV。
已知密度和质量,求体积:V = m/ρ。
单位换算示例:
铁的密度是 7.9×10 kg/m = 7.9g/cm 。
酒精的密度是 0.8g/cm = 0.8×10 kg/m 。
计算示例:
一块体积为 20cm 的铁块,质量是多少?(铁的密度是 7.9g/cm )
解:根据 m = ρV,可得 m = 7.9g/cm ×20cm = 158g。
一个质量为 500g 的瓶子,装满水后总质量为 1500g,求瓶子的容积。(水的密度是 1g/cm )
解:水的质量 m = 1500g - 500g = 1000g,根据 V = m/ρ,可得瓶子的容积 V = 1000g/1g/cm = 1000cm 。
随堂练习
某种物质组成的物体的______与它的______之比叫做这种物质的密度,密度的公式是______,国际单位是______。
水的密度是______kg/m ,它表示的物理意义是______。
体积为 1m 的冰块全部熔化成水后,水的质量是______kg,水的体积是______m 。(冰的密度是 0.9×10 kg/m )
一个铝块的质量是 54g,体积是 20cm ,则铝的密度是______g/cm ,合______kg/m 。
用天平和量筒测量某石块的密度,测得石块的质量为 50g,量筒中水的体积为 30cm ,放入石块后水和石块的总体积为 40cm ,则石块的密度是多少?
答案
质量;体积;ρ = m/V;kg/m
1.0×10 ;1 立方米水的质量是 1.0×10 千克
900;0.9
2.7;2.7×10
解:石块的体积 V = 40cm - 30cm = 10cm ,石块的密度 ρ = m/V = 50g/10cm = 5g/cm 。
总结
密度是物质的一种特性,定义为质量与体积之比,公式为 ρ = m/V,单位有 kg/m 和 g/cm ,两者的换算关系是 1g/cm = 1×10 kg/m 。
同种物质的密度与质量、体积无关,不同物质的密度一般不同,同种物质的密度还与状态有关。
测量物质的密度需要测量质量和体积,质量用天平测量,体积根据物体的形状选择合适的工具测量(刻度尺或量筒)。
密度在鉴别物质、计算质量或体积、选择材料等方面有广泛的应用。
通过实验探究和计算练习,掌握了密度的概念、测量方法和应用,提高了实验操作和数据分析能力。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.问题探究:不同物体的质量大小
问题 结果 归纳总结
体积相同的铝 块,质量一样吗 通过天平称量 发现质量一样 (1)体积相同的同
种物质,质量相同;
(2)体积不同的同
种物质,质量不同;
(3)体积相同的不
同物质,质量一般不
同
体积不同的铁 块,质量一样吗 通过天平称量 发现质量不一 样 问题 结果 归纳总结
体积相同的铝块 和铁块,质量一 样吗 通过天平称量 发现质量不一 样 (1)体积相同的同
种物质,质量相同;
(2)体积不同的同
种物质,质量不同;
(3)体积相同的不
同物质,质量一般不
同
2.实验探究:物体的质量与体积的关系
实验设计 选取不同体积的长方体组(如铝块、铁块、铜
块),测出其质量和体积,分别计算出单位体
积的质量,并进行比较
实验过程 (1)分别用电子天平测量长方体组中大小不
同的物块的质量,用刻度尺测量其尺寸并计算
其体积,填写在下面的表格中;
实验过程
数据处理
实验结论 (1)分析表中数据可知:
①物块的体积增大为原来的几倍,其质量也增
大为原来的几倍,质量与体积之比不变.
②铝块、铁块、铜块的质量与其体积的比值不
同,即不同物质组成的物体,其质量与体积的
比值一般不同.
(2)分析图像可知:铝块、铁块、铜块的图
像都是一条过原点的倾斜直线,即同种物质组
成的物体,其质量与体积成正比
交流讨论 “质量与体积的比值”就是“单位体积的质量”,
同种物质的质量与其体积的比值是一定的,即
物体的质量与其体积的比值反映了物质的一种
特性
典例1 [ 西安期末 ] 为了研究物质的某种物理属性,
同学们找来大小不同的蜡块和干松木做实验,得到的数
据如表所示.
实验序 号 蜡块 干松木
① 10 9 10 5
② 20 18 20 10
③ 30 27 30 15
④ 40 36 40 20
(1)在如图的方格纸中,用图线分
别把蜡块和干松木的质量随体积变化
的情况表示出来.
[答案] 如图所示.
[解析] 根据表中蜡块和干松木的体积和质量数据在方格
纸上描点,并用平滑的线进行连接.
(2)通过对比数据和分析图像, 可以得到:
结论1:同种物质,质量与体积的比值是______(选填“相等”
或“不相等”)的.
结论2:不同物质,质量与体积的比值是________
(选填“相等”或“不相等”)的.
相等
不相等
(3)由以上分析可知, 若测得另一干松木的质量为 ,
则它的体积应为____ .
80
[解析] 同种物质组成的物体,其质量与体积的比值相等,
由此可知,,解得 .
3.密度的概念
在物理学中,某种物质组成的物体的质量与其体积之比
叫作这种物质的密度,用符号 表示.
4.对密度概念的理解
(1)密度是物质的一种特性,在条件一定的情况下,每
种物质的密度是确定的.密度不随物体质量或体积的变化
而变化.
(2)不同物质的密度一般不同.
特别提醒
日常生活中,人们往往感觉密度大的物质“重”,密度小的
物质“轻”,比如,常说的“铁比棉花重”,实质上是指铁的
密度大于棉花的密度,真正的重或轻取决于物体的质量.
5.密度公式及单位
(1)密度公式: .变形公式:,.
(2)密度的单位
①国际单位: ,读作“千克每立方米”.
②常用单位: ,读作“克每立方厘米”.
.
换算过程: .
特别提醒
运用密度公式时的注意事项
(1)公式 是密度的定义式,适用于所有物体
(包括气体、液体和固体)密度的计算.
(2)质量、体积和密度必须对应同一物态的同一物体.
(3)单位统一,对应使用如下:
①质量单位用,体积单位用,则密度单位为 ;
②质量单位用,体积单位用,则密度单位为 .
教材深挖
物质密度的特点及规律
(1)密度表中固体、液体的密度标有常温、常压,气体
的密度标有 、一个标准大气压,这说明密度与温度、
压强等有关.
(2)一般情况下, ;常见液体中,水银的
密度最大(大于大多数固体的密度);常见金属中,铝
的密度最小;常见气体中,氢气的密度最小.
(3)同种物质的物态不同,其密度不同.当物质在不同物
态间转化时,其质量不变,但体积发生变化,密度也发
生改变.如常温常压下,水的密度为 ,变
为冰后密度为 ,密度变小,体积变大.
(4)不同种物质的密度可能相同,如冰和蜡的密度相同,
煤油和酒精的密度相同.
典例2 如图,放在一朵花上的
“全碳气凝胶”是我国科学家研制的迄今为止密
度最小的材料,密度只有 .某汽
3.2
车发动机采用密度为 的高强度合金材料制
造,质量为 ;若采用“全碳气凝胶”制造,需要“全
碳气凝胶”的质量为____ .
[解析] 由 可得发动机的体积为
,若采用“全碳气凝胶”制
造, ,则需要“全碳气凝
胶”的质量为
.
1.利用密度知识可以鉴别物质类别
根据密度公式,把测得的物体的质量和体积代入即可求
出物质的密度,再从密度表中查出该密度的物质,二者
对比即可以进行物质的鉴别.
此方法为粗略鉴别,若想准确鉴别,还需要配合
其他方法.
2.密度在生产生活中的应用
(1)根据密度大小选择合适的材料(物质).为了减轻车
辆、飞机的自重,常选择密度较小的合金材料或复合材
料;产品包装则应选择密度较小的泡沫塑料等.
(2)根据密度,鉴别优劣.酒、牛奶等物质,其产品质量
的好坏和密度有关,因此其密度是质检的重要参数.农业
中还可以用盐水来选种,饱满健壮的种子在水中会因为
密度大而下降,干瘪的种子会浮在水面上.
(3)测量密度,确定矿藏种类.勘探队员通过采集样品的
密度等信息,确定矿藏种类及其经济价值.
典例3 一棱长为 的正方体实心金属块,其质量为
.该金属块是由下表中的某一金属物质组成的,则组
成该金属块的物质是( )
常温下一些金属的密度/
金 19.3 铝 2.7
银 10.5 铁 7.9
C
A.金 B.银 C.铝 D.铁
[解析] 该金属的密度
,因此该金
属是铝.
知识点1 认识密度
1. [2023·海南]下列现象中,密度变大的是( B )
A. 铁棒磨成针
B. 冰熔化成水
C. 橡皮泥捏成小船
D. 氧气瓶内的氧气用了一段时间
B
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 密度公式因能被写成如图所示的样式,而被称为“物理最
美公式”,下列关于密度的说法正确的是( B )
A. 铁比铝“重”,“重”指的是铁的质量比铝的质量大
B. 一罐氧气用掉部分后,罐内氧气的质量变
小,密度变小
C. 一块砖被切成体积相等的两块后,砖的密度变为原来的一半
D. 利用铝合金材料制作列车车体,因为它的密度大,行驶时列车更稳
B
1
2
3
4
5
6
7
8
9
10
11
12
13
知识点2 密度的计算
3. [2024·济南模拟]加气混凝土砌块是一种轻质多孔、防火性
能良好、具有一定抗震能力的新型建筑材料,还具有环保
等优点,被广泛使用于高层框架结构建筑中。现有一块加
气混凝土砌块,其体积为1.08×104 cm3,质量为6.48 kg。该加气混凝土砌块的密度为 。
0.6×103 kg/m3(或0.6 g/cm3)
1
2
3
4
5
6
7
8
9
10
11
12
13
4. 某AD钙奶的密度为1.05×103 kg/m3,其物理含义是
。
它的包装盒上标注了净含量450 mL,瓶中所装AD钙奶的
质量为 g。将此瓶AD钙奶喝掉一半以后,剩余
AD钙奶的密度将 (填“变大”“变小”或“不
变”)。
每
立方米AD钙奶的质量是1.05×103 kg
472.5
不变
1
2
3
4
5
6
7
8
9
10
11
12
13
【点拨】
AD钙奶的密度ρ=1.05×103 kg/m3,它表示的物理含义是每立方米AD钙奶的质量是1.05×103 kg;它的包装盒上标注了净含量V=450 mL=450 cm3,根据密度公式得,瓶中所装AD钙奶的质量m=ρV=1.05 g/cm3×450 cm3=472.5 g;喝掉一半后,其密度不变。
1
2
3
4
5
6
7
8
9
10
11
12
13
5. 如图所示是小明在探究甲、乙两种不同液体的质量与体积
的关系时得出的图像,由图像可知,甲、乙两种液体的密
度之比为 ,其中乙的密度为 kg/m3,
一只瓶子刚好能装下1 kg的液体甲,
则这只瓶子 (填“能”或
“不能”)装下1 kg的液体乙。
4∶1
0.5×103
不能
(第5题)
1
2
3
4
5
6
7
8
9
10
11
12
13
【点拨】
由图像可知,当体积V=4 cm3时,对应的质量m甲=
8.0 g、m乙=2.0 g,由ρ=可得,甲、乙两种液体的密度之比ρ甲∶ρ乙=∶=m甲∶m乙=8.0 g∶2.0 g=4∶1;其中乙的密度ρ乙===0.5 g/cm3=0.5×103 kg/m3;由ρ=可得V=,质量相同时,密度小的体积大,一只瓶子刚好能装下1 kg的液体甲,则这只瓶子不能装下1 kg的液体乙。
1
2
3
4
5
6
7
8
9
10
11
12
13
知识点3 密度的应用
6. [现代科技]中国海上巨型风机——巨无霸SL5000是史上最
大的单体风力发电机,如图所示,它的每个叶片长62 m,
它转动起来能够扫过将近两个足球场大的面积。为了让风
更易带动起扇叶,制成叶片的材料应该具有( C )
A. 较大的质量 B. 较低的熔点
C. 尽量小的密度 D. 较好的吸热性
(第6题)
C
1
2
3
4
5
6
7
8
9
10
11
12
13
7. [传统文化]山西绛州澄泥砚,始创于唐代,是中国“四大
名砚”之一。如图所示是绛州澄泥砚传承人蔺涛正在利用
汾河下游的澄泥雕刻砚台的场景,雕刻过程中不发生变化
的是( B )
B
A. 澄泥的质量
B. 澄泥的密度
C. 澄泥的体积
D. 澄泥的形状
1
2
3
4
5
6
7
8
9
10
11
12
13
8. [2024·西安开学]如表是部分物质在0 ℃、标准大气压下的
密度表,小刚由此提出了对密度的一些看法,你认为正确
的是( D )
0 ℃、标准大气压下部分物质的密度/(kg/m3) 水 1.0×103 冰 0.9×103
水银 13.6×103 干松木 0.5×103
酒精 0.8×103 铜 8.9×103
煤油 0.8×103 铝 2.7×103
1
2
3
4
5
6
7
8
9
10
11
12
13
A. 固态物质的密度一定比液态物质的密度大
B. 同种物质的密度一定相同
C. 质量相同的水银和酒精,水银体积较大
D. 体积相同的实心铜块和铝块,铜块的质量大
1
2
3
4
5
6
7
8
9
10
11
12
13
固态物质干松木的密度小于液态物质水的密度,A错
误;水和冰是同种物质,但密度不同,B错误;质量相同
的水银和酒精,因为ρ水银>ρ酒精,由V=可知,水银的体
积较小,C错误;体积相同的实心铜块和铝块,因为m=
ρV,ρ铜>ρ铝,所以铜块的质量大,D正确。
【答案】D
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
9. [2024·泰州月考]野战部队携带的压缩饼干与普通饼干相
比,好处在于质量相等的情况下,它的密度 (填
“较大”或“较小”,下同),体积 。如图所
示,点燃蜡烛会使上方的扇叶旋转起来,这是因为蜡烛的
火焰使附近空气的温度升高,体积膨胀,空气的密度
(填“变大”或“变小”),所以热空气
(填“上升”或“下降”)形成气流,
气流流过扇叶时,带动扇叶转起来。
较大
较小
变
小
上升
1
2
3
4
5
6
7
8
9
10
11
12
13
【点拨】
压缩饼干与普通饼干相比,好处是在质量相等的情况下,物质间隙较小,所以体积较小,由ρ=可知,质量相等的情况下,它的密度较大。点燃蜡烛,附近的空气吸收热量,温度升高,体积膨胀,密度变小,密度小的热空气上升,形成对流,使扇叶转动。
1
2
3
4
5
6
7
8
9
10
11
12
13
10. [2024·高新一中期中]甲、乙两个实心金属块,它们的体
积之比为5∶4,将它们分别放在已调平的天平左右盘中,
天平恰好平衡,则甲和乙的质量之比为 ,密度之
比为 ;若将甲切去五分之二,将乙切去四分之
三,那么甲和乙剩余部分的密度之比是 ,甲和乙
剩余部分的质量之比是 。某医院急诊室的氧气
瓶中,氧气的密度为6 kg/m3,给急救病人供氧用去了氧
气质量的三分之一,则瓶内剩余氧气的密度为 . kg/m3。
1∶1
4∶5
4∶5
12∶5
4
1
2
3
4
5
6
7
8
9
10
11
12
13
【点拨】
天平平衡,说明两物体质量相同,所以甲和乙的质量之比为1∶1,密度之比===;因为密度是物质的一种特性,与物质的质量、体积的大小无关,所以切去一部分后,密度之比不变,仍为4∶5,因将甲切去五分之二,将乙切去四分之三,则甲和乙剩余部分的质量之比===12∶5。
1
2
3
4
5
6
7
8
9
10
11
12
13
原来氧气的密度为6 kg/m3,给急救病人供氧用去了氧气质量
的,氧气质量变为原来的,而氧气的体积保持不变(等于氧
气瓶的容积),根据ρ=可知,氧气的密度变为原来的,则
瓶内剩余氧气的密度ρ'=ρ=×6 kg/m3=4 kg/m3。
1
2
3
4
5
6
7
8
9
10
11
12
13
11. [2023·济宁]在测定某液体密度时,小明做了两次实验并
做了如下记录,则液体的密度ρ= g/cm3,容器的质
量m= g。
次数 液体的体积V/cm3 容器和液体的总质量m/g
1 58 79
2 107 128
1
21
1
2
3
4
5
6
7
8
9
10
11
12
13
【点拨】
由题意知,两次实验液体的质量之差Δm=128 g-79 g=49 g,液体体积之差ΔV=107 cm3-58 cm3=49 cm3,液体的密度ρ===1 g/cm3,由ρ=得,第一次实验时液体的质量m1=ρV1=1 g/cm3×58 cm3=58 g,容器的质量m=m总1-m1=79 g-58 g=21 g。
1
2
3
4
5
6
7
8
9
10
11
12
13
12. [2024·盐城月考]中国的粮食安全有保障,已连续多年增
产,但我们仍然要厉行节约。如图所示,小华家的晒谷
场上有一堆稻谷,体积为5 m3。为了估测这堆稻谷的质
量,他用一只空桶平平地装满一桶稻谷,测得桶中稻谷
的质量为9.9 kg;再用这只桶装满水,测得桶中水的质
量为9 kg。(ρ水=1.0×103 kg/m3)求:
1
2
3
4
5
6
7
8
9
10
11
12
13
【解】根据ρ=可得,桶中的水的体积
V水===9×10-3 m3。
(1)装满水时,桶中水的体积。
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)稻谷的密度。
【解】桶中稻谷的体积V0=V水=9×10-3 m3,
稻谷的密度ρ===1.1×103 kg/m3。
(3)这堆稻谷的总质量。
【解】这堆稻谷的总质量m总=ρV总=1.1×103 kg/m3× 5 m3=5.5×103 kg。
1
2
3
4
5
6
7
8
9
10
11
12
13
13. [科学推理]如图甲所示,A组是由材料、大小和厚度均相
同的小正四棱柱整齐叠加在一起的一个大正四棱柱(忽略
中间的缝隙),其底面积为100 cm2;B组是由另一种材料
制成的正四棱柱,其密度为0.75×103 kg/m3。现从A组
上逐块取下小正四棱柱并叠放在B组正四棱柱上,A、B
两组正四棱柱的质量随A组大正四棱柱减小的高度h的变
化关系图像如图乙所示,由图像可知,A组小正四棱柱
的密度为 kg/m3,B组正四棱柱的体积
为 m3。
0.8×103
1.28×103
1
2
3
4
5
6
7
8
9
10
11
12
13
谢谢观看!
同课章节目录
