2.1.2.1代数式 课件(共35张PPT)
文档属性
| 名称 | 2.1.2.1代数式 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 20:51:14 | ||
图片预览











文档简介
(共35张PPT)
2.1.2.1代数式
第2章 整式及其加减
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
2.1.2.1 代数式
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
上节课我们学习了用字母表示数,知道用字母可以表示数量关系、运算律、计算公式等,比如 “x 与 y 的和” 可以表示为\(x + y\),“长方形的面积” 可以表示为\(ab\)(a 为长,b 为宽)。这些用字母和运算符号组成的式子,就是我们今天要学习的代数式。
学习目标
理解代数式的概念,能准确判断一个式子是否为代数式。
掌握代数式的书写规范,能根据数量关系列出代数式。
能解释代数式的实际意义,体会代数式在表示数量关系中的作用。
培养抽象思维能力和符号意识,感受数学的简洁性。
课堂导入
在日常生活中,我们经常会遇到各种需要用数学式子表示的数量关系。例如:
买一个笔记本需要 x 元,买一支钢笔需要 y 元,那么买 2 个笔记本和 3 支钢笔一共需要多少钱?(答案:\(2x + 3y\)元)
一个正方体的棱长为 a 厘米,它的表面积是多少平方厘米?(答案:\(6a^2\)平方厘米)
像\(2x + 3y\)、\(6a^2\)这样的式子,都是用字母和运算符号连接而成的,它们都叫做代数式。代数式是代数中非常重要的概念,它可以帮助我们更简洁、更一般地表示数量关系。
知识点:代数式的概念
定义
用运算符号(加、减、乘、除、乘方、开方等)把数或表示数的字母连接而成的式子叫做代数式。
单独的一个数或者一个字母也叫做代数式。
例如:
单独的数:5、-3、0.7 等都是代数式。
单独的字母:a、b、x、y 等都是代数式。
数与字母、字母与字母用运算符号连接的式子:\(a + b\)、\(3x - 2y\)、\(m^2\)、\(\frac{x}{y}\)(\(y 0\))、\(2(a + b)\)等都是代数式。
注意事项
代数式中不含有等号或不等号(如 “=”“≠”“>”“<”“≥”“≤” 等),含有这些符号的式子不是代数式。例如,\(x + 2 = 5\)、\(3a b\)都不是代数式。
代数式中的运算符号是指我们学过的加、减、乘、除、乘方等,开方运算在后续会学习。
代数式的书写要遵循一定的规范,这在后续会详细讲解。
知识点:代数式的书写规范
代数式的书写要简洁、规范,便于理解和运算,具体规则如下:
数与字母、字母与字母相乘:乘号可以省略不写,或用 “ ” 表示,但数必须写在字母前面。
例如:\(a 5\)应写成\(5a\)或\(5 ·a\),不能写成\(a5\);\(a b\)应写成\(ab\)或\(a ·b\)。
带分数与字母相乘:带分数要先化成假分数,再与字母相乘。
例如:\(2\frac{1}{3} x\)应写成\(\frac{7}{3}x\),不能写成\(2\frac{1}{3}x\)。
字母与 1 或 - 1 相乘:1 可以省略不写,-1 中的 “1” 也可以省略不写。
例如:\(1 a\)应写成\(a\);\(-1 a\)应写成\(-a\)。
含有除法运算:除法运算通常写成分数形式。
例如:\(a ·b\)(\(b 0\))应写成\(\frac{a}{b}\);\(x ·3\)应写成\(\frac{x}{3}\)。
代数式后面有单位:若代数式是和或差的形式,要给代数式加括号。
例如:\(a + b\)米应写成\((a + b)\)米,不能写成\(a + b\)米;\(m - n\)千克应写成\((m - n)\)千克。
相同字母的乘积:一般写成乘方的形式。
例如:\(a a\)应写成\(a^2\);\(x x x\)应写成\(x^3\)。
知识点:代数式的意义
代数式的意义是指代数式所表示的数量关系或实际含义。解释代数式的意义时,可以从以下两个方面入手:
从运算的角度解释:说明代数式中包含的运算以及运算顺序。
例如:\(3a + 2b\)可以解释为 “a 的 3 倍与 b 的 2 倍的和”。
结合实际背景解释:赋予代数式中的字母实际意义,从而解释整个代数式的意义。
例如:若 a 表示一个苹果的质量(单位:克),b 表示一个橘子的质量(单位:克),则\(3a + 2b\)可以解释为 “3 个苹果和 2 个橘子的总质量(单位:克)”。
例题解析
例 1:判断下列各式是不是代数式:
(1)\(3x + 5\) (2)\(x - 2 = 7\) (3)\(a\) (4)\(5 3\) (5)\(\frac{1}{2}m^2n\)
解:(1)\(3x + 5\)是用加号把数和字母连接而成的式子,是代数式;
(2)\(x - 2 = 7\)中含有等号,不是代数式;
(3)\(a\)是单独的一个字母,是代数式;
(4)\(5 3\)中含有不等号,不是代数式;
(5)\(\frac{1}{2}m^2n\)是用乘号(省略)把数和字母连接而成的式子,是代数式。
例 2:根据下列数量关系列出代数式:
(1)x 的 2 倍与 y 的差;
(2)a 的平方与 b 的立方的和;
(3)m 与 n 的和的倒数;
(4)比 x 的\(\frac{1}{3}\)大 5 的数。
解:(1)x 的 2 倍是\(2x\),与 y 的差是\(2x - y\);
(2)a 的平方是\(a^2\),b 的立方是\(b^3\),它们的和是\(a^2 + b^3\);
(3)m 与 n 的和是\(m + n\),其倒数是\(\frac{1}{m + n}\)(\(m + n 0\));
(4)x 的\(\frac{1}{3}\)是\(\frac{1}{3}x\),比它大 5 的数是\(\frac{1}{3}x + 5\)。
例 3:下列代数式的书写是否规范?若不规范,请改正。
(1)\(a 7\) (2)\(m ·n\) (3)\(2\frac{3}{4}x\) (4)\(x + y\)千克 (5)\(1a\)
解:(1)不规范,数应写在字母前面,乘号省略,改正为\(7a\);
(2)不规范,除法运算应写成分数形式,改正为\(\frac{m}{n}\)(\(n 0\));
(3)不规范,带分数应化成假分数,改正为\(\frac{11}{4}x\);
(4)不规范,代数式是和的形式且后面有单位,应加括号,改正为\((x + y)\)千克;
(5)不规范,1 与字母相乘时 1 应省略,改正为\(a\)。
例 4:解释下列代数式的意义:
(1)\(3a + 2\);
(2)\(\frac{s}{t}\)(\(t 0\))。
解:(1)从运算角度:\(3a + 2\)表示 a 的 3 倍与 2 的和;
从实际背景角度:若 a 表示一支铅笔的价格(单位:元),则\(3a + 2\)表示买 3 支铅笔和一个 2 元橡皮的总价格(单位:元)。
(2)从运算角度:\(\frac{s}{t}\)表示 s 除以 t 的商;
从实际背景角度:若 s 表示一段路程(单位:千米),t 表示走完这段路程所用的时间(单位:小时),则\(\frac{s}{t}\)表示这段路程的平均速度(单位:千米 / 小时)。
小练习
判断下列各式是不是代数式:
(1)\(5x - 3y\) (2)\(4 + 5 = 9\) (3)\(-8\) (4)\(x^2 + 2x - 1\) (5)\(b ¤a\)
根据数量关系列出代数式:
(1)a 与 b 的差的平方;
(2)x 的 5 倍与 y 的\(\frac{2}{3}\)的和;
(3)比 m 的相反数小 3 的数;
(4)a、b 两数的平方和减去它们积的 2 倍。
改正下列代数式书写不规范的地方:
(1)\(x5\) (2)\(m ·n\)(可省略乘号时) (3)\(3\frac{1}{2}a\) (4)\((a + b) ·c\)(\(c 0\)) (5)\(1x^2y\)
解释下列代数式的意义:
(1)\(2a - 5\);
(2)\(a^2 - b^2\)。
思考讨论
代数式与我们之前学过的用字母表示数有什么关系?
代数式是用字母表示数的延伸和具体化,用字母表示数是代数式的基础。用字母表示数可以表示一个或一类数,而代数式则是用运算符号把数和表示数的字母连接起来,更全面地表示了数量之间的运算关系。例如,用字母 a 表示一个数是用字母表示数,而\(2a + 3\)则是一个代数式,它表示了这个数的 2 倍与 3 的和。
如何避免在列代数式时出现错误?
列代数式时,要仔细分析数量关系,明确运算顺序。可以先找出关键词,如 “和”“差”“积”“商”“倍”“分”“平方”“立方” 等,确定运算的类型和顺序;同时,要注意代数式的书写规范,避免因书写不规范导致误解。对于复杂的数量关系,可以先分步表示,再组合成一个代数式。
课堂小结
代数式的概念:用运算符号把数或表示数的字母连接而成的式子,单独的一个数或一个字母也是代数式。
代数式的书写规范:包括数与字母、字母与字母相乘的写法,带分数的处理,除法运算的表示,单位的添加等。
代数式的意义:可以从运算角度和实际背景角度进行解释,体现了代数式表示数量关系的一般性和灵活性。
代数式中不含有等号或不等号,这是判断一个式子是否为代数式的重要依据。
课后作业
教材 P59 练习 1、2、3 题。
下列各式中,哪些是代数式?
(1)\(3x + 7\) (2)\(2x - 1 = 6\) (3)\(0\) (4)\(\frac{a + b}{c}\)(\(c 0\)) (5)\(x y\)
用代数式表示:
(1)x 的\(\frac{1}{2}\)与 y 的 3 倍的差;
(2)a、b 两数的和与它们的差的积;
(3)m 的平方与 n 的立方的倒数的和;
(4)比 x 大 10% 的数。
赋予代数式\(4a\)一个实际意义。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.了解代数式的概念,能用代数式表示简单问题中的数量关系;
2.在具体情境中,能求出代数式的值,并解释它的实际意义.
3.通过列代数式,初步体会数学中抽象概括的思维方法.
学习目标
3.图中由长方形和正方形拼成的大正方形的面积为____________;
我们还可以这样想,图中大正方形的边长是_____,因此它的面积是
______.
1.深圳的气温为 x ℃,北京的气温比深圳低4℃,北京的气温为_____℃.
2.深圳到北京的距离是 s km,高铁的速度为 300 km/h,从深圳到北京需_____h.
复习回顾
a +2ab+b
a+b
(a+b)
a
b
a
b
x-4
进行新课
知识点一
代数式的概念及书写方式
观察下列这些式子,它们有何共同特点?
41472n,2k, 2k-1,a+b,(a+b) , , ,
含有数字或字母
含有运算符号
这些式子都是由数、字母用加、减、乘、除及乘方等运算符号连接而成.
1.代数式的概念
41472n,2k, 2k-1,a+b,(a+b) , , ,
像这样用加、减、乘、除及乘方等运算符号把数或表示数的字母连接而成的式子,叫作代数式.
代数式
练一练:下列各式中哪些是代数式?哪些不是?
方法:①代数式中不含表示关系的符号.
(“=”,“>”,“<”,“ ”,“ ”,“≠”)
②单独的一个数或字母也是代数式.
2.代数式的书写方法
(1)练习簿的单价为a元,100本练习簿的总价是______元. b本练习簿的总价是______元.
100a
①若出现乘号,可写成“·”或不写.
数字与字母相乘时,数字写在字母前;
字母与字母相乘时,相同字母写成幂的形式;数字与数字相乘时,乘号“×”不能省略.
ab
(2)某篮球运动员个子高,经测量他通常跨一步的距离1米,若取向前为正,向后为负,那么他向前跨a步为____米,向后跨a步为____米.
a
-a
②当“1”与任何字母相乘时,“1”可省略不写;
当“-1”乘以字母时,只要在那个字母前加上“-”号即可.
(3)若每斤苹果 元,则买m斤苹果需______元.
③带分数与字母相乘时,要将带分数化成假分数.
(4)小明的家离学校 s 千米,小明骑车上学,若每小时行
10千米,则需_____时.
④如果式中出现除法,如s÷v,一般写成 的形式.
(5)练习簿的单价为0.5元,圆珠笔的单价是3.2元,买a本练习簿和b支笔的总价是___________元.
(0.5a+3.2b)
⑤如果式子后面有单位且式子是和或差的形式,式子要用小括号括起来.
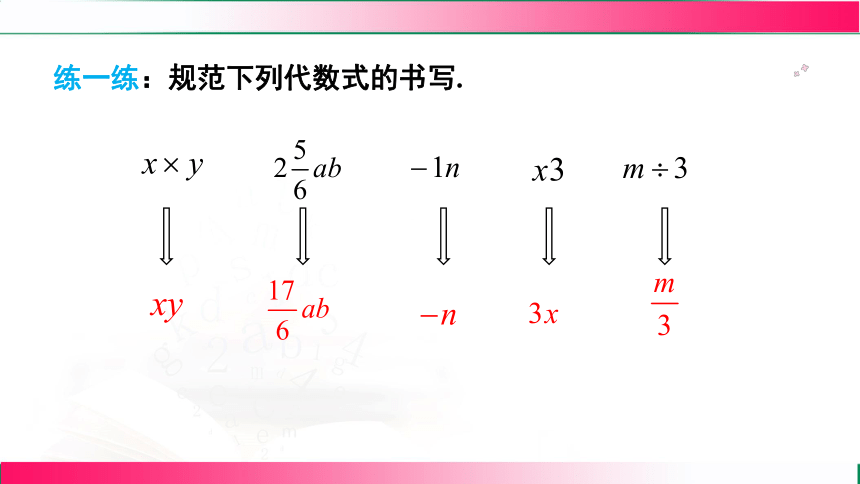
练一练:规范下列代数式的书写.
知识点二
列代数式
例
1
用代数式表示:
(1)某商店上月收入x元,本月收入比上月的2倍还多5万元,该商店本月收入为__________元;
(2)一件a元的衬衫,降价10%后,价格为___________元.
列代数式就是把实际问题中的数量关系,用含有数、字母和运算符号的式子表示出来.
2x+50000
(1-10%)a
例
2
用代数式表示:
(1)把a本书分给若干名学生,若每人5本,还剩余3本,求学生数;
解:(1)因为从a本书中去掉3本,按每人5本正好分完,所以学生数为 .
例
2
用代数式表示:
(2)某次高铁列车先以290 km/h的速度运行a h,后以310 km/h的速度运行b h.求它行驶的路程.
解:(2)该次高铁列车行驶的路程为
(290a+310b)km
归纳:列代数式要点
要抓住关键词语,将问题中的数量关系正确地转换为对应的运算.如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
理清语句层次,明确运算顺序;
掌握实际问题中的基本量的关系和公式;
根据运算顺序及与数量关系有关的“的”“与”等字,逐层分析,一步步列出代数式.
1
2
3
4
知识点三
代数式的意义
例
3
说出下列代数式的意义:
(1)如果圆珠笔每支售价a元,练习簿每本售价b元,那么3a+4b表示什么?
(2)如果长方形的长、宽分别为a,b,那么(a+1)b表示什么?
解:(1)3 支圆珠笔与4本练习簿的总金额.
(2)长为a+1、宽为b的长方形的面积.
练一练:说出下列代数式的意义.
(1)m2-n2; (2)7(x+y)(x-y);
(3) ; (4)2x2-3y2.
解:(1)m,n两数的平方差;
(2)x,y两数的和与它们的差的乘积的7倍;
(3)a、b两数的和除以它们的差的商;
(4)x的平方的2倍与y的平方的3倍的差.
随堂演练
1.下列式子:①x÷y;②2m-1个;③-xy2;④mn2.其中格式书写正确的个数是( )A.1 B.2 C.3 D.4
A
2.一件商品的进价是a元,提价30%后出售,则这件商品的售价是( )
A.0.7a 元 B.a 元
C.1.3a 元 D.3a 元
C
【选自教材P65练习 第1题】
3.用代数式表示:
(1)购买单价为a元的贺年卡n张,付出50元,应找回_______元.
(2)女儿今年x岁,妈妈的年龄是女儿的3倍,3年后妈妈的年龄是_______岁.
(3)苹果每千克售价p元,买5kg 以上9折优惠. 现买 15 kg,应付________元.
(4)被3除所得的商为n、余数为2的整数为__________(用n表示).
(50-na)
(3x+3)
13.5p
3n+2
4.用代数式表示:
(1)一桶质量为 m kg的盐水,含盐为 p%,则这桶盐水中水的质量为多少?
(2)某超市一种品牌的矿泉水进价为每瓶a元,零售时每瓶加价20%,每瓶的零售价是多少元?
(3)长方体的长为3m,宽和高都是 a m,则这个长方体的体积是多少?
【选自教材P65~66练习 第2题】
解:(1)(1-p%)m kg.
(2)(1+20%)a 元.
(3)3a2 m3.
5.如图,一组有规律的图案中,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,…,则第n(n是正整数)个图案由多少个基础图形组成?
【选自教材P66练习 第3题】
解:第1个图案中基础图形的个数为 3+1;第2 个图案中基础图形的个数是 3×2+1;第3个图案中基础图形的个数是 3×3+1……所以,第n个图案中基础图形的个数是 3n+1.
1星题 基础练
知识点1 代数式的概念及书写规则
1.下列式子中:;;;; ;
;; ,属于代数式的有( )
A
A.5个 B.6个 C.7个 D.8个
2.下列代数式,表示正确的是( )
C
A. B. C. D. 元
3.下列式子书写不规范,请改正过来.
(1) _____;
(2) ____;
(3) ______;
(4) __.
知识点2 列代数式
4.用代数式表示:
(1)比与 的积的2倍小5的数为_________;
(2)设某工程总量为1,甲单独完成该工程需 天,则甲的工作
效率可以表示为__;
(3)某商品打八折后价格为 元,这件商品的原价为_ ___元.
知识点3 代数式的意义
5.[2024·福州期中]代数式 用语言叙述正确的是
( )
A
A.的平方与 的平方的4倍的和
B.的平方与4的和乘以 的平方
C.与 的和的平方
D.与 的平方和
2星题 中档练
6.数学文化 《九章算术》中记载一问题:“今有共买物,人
出八,盈三;人出七,不足四.问人数、物价各几何?”意思
是:今有若干人合伙购物,每人出8钱,会多 3钱;每人出7
钱,又差4钱.问人数、物价各是多少?设人数为 ,则物价为
( )
D
A.钱 B.钱 C.钱 D. 钱
7.一台“节能电视”成本价为 元,销售价比成本价增加了
,因促销活动,销售价降价 出售,那么每台电视机
的实际售价为____元.
8.[2024·合肥校级一模]将字母“C”,“ ”按照如图所示的
规律摆放,其中第1个图形中有1个字母C,有4个字母 ;第
2个图形中有2个字母C,有6个字母 ;第3个图形中有3个字
母C,有8个字母 根据此规律解答下面的问题:
(1)第4个图形中有___个字母C,有____个字母 ;
4
10
(2)第个图形中有___个字母C,有_________个字母
(用含 的式子表示);
(3)第2 025个图形中有_______个字母C,有_______个字母 .
课堂小结
代数式
概念
应用
用加、减、乘、除及乘方等运算符号把数或表示数的字母连接而成的式子叫作代数式. 单个的数或字母也是代数式.
列代数式
代数式的意义
注意书写规范
谢谢观看!
2.1.2.1代数式
第2章 整式及其加减
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
2.1.2.1 代数式
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
上节课我们学习了用字母表示数,知道用字母可以表示数量关系、运算律、计算公式等,比如 “x 与 y 的和” 可以表示为\(x + y\),“长方形的面积” 可以表示为\(ab\)(a 为长,b 为宽)。这些用字母和运算符号组成的式子,就是我们今天要学习的代数式。
学习目标
理解代数式的概念,能准确判断一个式子是否为代数式。
掌握代数式的书写规范,能根据数量关系列出代数式。
能解释代数式的实际意义,体会代数式在表示数量关系中的作用。
培养抽象思维能力和符号意识,感受数学的简洁性。
课堂导入
在日常生活中,我们经常会遇到各种需要用数学式子表示的数量关系。例如:
买一个笔记本需要 x 元,买一支钢笔需要 y 元,那么买 2 个笔记本和 3 支钢笔一共需要多少钱?(答案:\(2x + 3y\)元)
一个正方体的棱长为 a 厘米,它的表面积是多少平方厘米?(答案:\(6a^2\)平方厘米)
像\(2x + 3y\)、\(6a^2\)这样的式子,都是用字母和运算符号连接而成的,它们都叫做代数式。代数式是代数中非常重要的概念,它可以帮助我们更简洁、更一般地表示数量关系。
知识点:代数式的概念
定义
用运算符号(加、减、乘、除、乘方、开方等)把数或表示数的字母连接而成的式子叫做代数式。
单独的一个数或者一个字母也叫做代数式。
例如:
单独的数:5、-3、0.7 等都是代数式。
单独的字母:a、b、x、y 等都是代数式。
数与字母、字母与字母用运算符号连接的式子:\(a + b\)、\(3x - 2y\)、\(m^2\)、\(\frac{x}{y}\)(\(y 0\))、\(2(a + b)\)等都是代数式。
注意事项
代数式中不含有等号或不等号(如 “=”“≠”“>”“<”“≥”“≤” 等),含有这些符号的式子不是代数式。例如,\(x + 2 = 5\)、\(3a b\)都不是代数式。
代数式中的运算符号是指我们学过的加、减、乘、除、乘方等,开方运算在后续会学习。
代数式的书写要遵循一定的规范,这在后续会详细讲解。
知识点:代数式的书写规范
代数式的书写要简洁、规范,便于理解和运算,具体规则如下:
数与字母、字母与字母相乘:乘号可以省略不写,或用 “ ” 表示,但数必须写在字母前面。
例如:\(a 5\)应写成\(5a\)或\(5 ·a\),不能写成\(a5\);\(a b\)应写成\(ab\)或\(a ·b\)。
带分数与字母相乘:带分数要先化成假分数,再与字母相乘。
例如:\(2\frac{1}{3} x\)应写成\(\frac{7}{3}x\),不能写成\(2\frac{1}{3}x\)。
字母与 1 或 - 1 相乘:1 可以省略不写,-1 中的 “1” 也可以省略不写。
例如:\(1 a\)应写成\(a\);\(-1 a\)应写成\(-a\)。
含有除法运算:除法运算通常写成分数形式。
例如:\(a ·b\)(\(b 0\))应写成\(\frac{a}{b}\);\(x ·3\)应写成\(\frac{x}{3}\)。
代数式后面有单位:若代数式是和或差的形式,要给代数式加括号。
例如:\(a + b\)米应写成\((a + b)\)米,不能写成\(a + b\)米;\(m - n\)千克应写成\((m - n)\)千克。
相同字母的乘积:一般写成乘方的形式。
例如:\(a a\)应写成\(a^2\);\(x x x\)应写成\(x^3\)。
知识点:代数式的意义
代数式的意义是指代数式所表示的数量关系或实际含义。解释代数式的意义时,可以从以下两个方面入手:
从运算的角度解释:说明代数式中包含的运算以及运算顺序。
例如:\(3a + 2b\)可以解释为 “a 的 3 倍与 b 的 2 倍的和”。
结合实际背景解释:赋予代数式中的字母实际意义,从而解释整个代数式的意义。
例如:若 a 表示一个苹果的质量(单位:克),b 表示一个橘子的质量(单位:克),则\(3a + 2b\)可以解释为 “3 个苹果和 2 个橘子的总质量(单位:克)”。
例题解析
例 1:判断下列各式是不是代数式:
(1)\(3x + 5\) (2)\(x - 2 = 7\) (3)\(a\) (4)\(5 3\) (5)\(\frac{1}{2}m^2n\)
解:(1)\(3x + 5\)是用加号把数和字母连接而成的式子,是代数式;
(2)\(x - 2 = 7\)中含有等号,不是代数式;
(3)\(a\)是单独的一个字母,是代数式;
(4)\(5 3\)中含有不等号,不是代数式;
(5)\(\frac{1}{2}m^2n\)是用乘号(省略)把数和字母连接而成的式子,是代数式。
例 2:根据下列数量关系列出代数式:
(1)x 的 2 倍与 y 的差;
(2)a 的平方与 b 的立方的和;
(3)m 与 n 的和的倒数;
(4)比 x 的\(\frac{1}{3}\)大 5 的数。
解:(1)x 的 2 倍是\(2x\),与 y 的差是\(2x - y\);
(2)a 的平方是\(a^2\),b 的立方是\(b^3\),它们的和是\(a^2 + b^3\);
(3)m 与 n 的和是\(m + n\),其倒数是\(\frac{1}{m + n}\)(\(m + n 0\));
(4)x 的\(\frac{1}{3}\)是\(\frac{1}{3}x\),比它大 5 的数是\(\frac{1}{3}x + 5\)。
例 3:下列代数式的书写是否规范?若不规范,请改正。
(1)\(a 7\) (2)\(m ·n\) (3)\(2\frac{3}{4}x\) (4)\(x + y\)千克 (5)\(1a\)
解:(1)不规范,数应写在字母前面,乘号省略,改正为\(7a\);
(2)不规范,除法运算应写成分数形式,改正为\(\frac{m}{n}\)(\(n 0\));
(3)不规范,带分数应化成假分数,改正为\(\frac{11}{4}x\);
(4)不规范,代数式是和的形式且后面有单位,应加括号,改正为\((x + y)\)千克;
(5)不规范,1 与字母相乘时 1 应省略,改正为\(a\)。
例 4:解释下列代数式的意义:
(1)\(3a + 2\);
(2)\(\frac{s}{t}\)(\(t 0\))。
解:(1)从运算角度:\(3a + 2\)表示 a 的 3 倍与 2 的和;
从实际背景角度:若 a 表示一支铅笔的价格(单位:元),则\(3a + 2\)表示买 3 支铅笔和一个 2 元橡皮的总价格(单位:元)。
(2)从运算角度:\(\frac{s}{t}\)表示 s 除以 t 的商;
从实际背景角度:若 s 表示一段路程(单位:千米),t 表示走完这段路程所用的时间(单位:小时),则\(\frac{s}{t}\)表示这段路程的平均速度(单位:千米 / 小时)。
小练习
判断下列各式是不是代数式:
(1)\(5x - 3y\) (2)\(4 + 5 = 9\) (3)\(-8\) (4)\(x^2 + 2x - 1\) (5)\(b ¤a\)
根据数量关系列出代数式:
(1)a 与 b 的差的平方;
(2)x 的 5 倍与 y 的\(\frac{2}{3}\)的和;
(3)比 m 的相反数小 3 的数;
(4)a、b 两数的平方和减去它们积的 2 倍。
改正下列代数式书写不规范的地方:
(1)\(x5\) (2)\(m ·n\)(可省略乘号时) (3)\(3\frac{1}{2}a\) (4)\((a + b) ·c\)(\(c 0\)) (5)\(1x^2y\)
解释下列代数式的意义:
(1)\(2a - 5\);
(2)\(a^2 - b^2\)。
思考讨论
代数式与我们之前学过的用字母表示数有什么关系?
代数式是用字母表示数的延伸和具体化,用字母表示数是代数式的基础。用字母表示数可以表示一个或一类数,而代数式则是用运算符号把数和表示数的字母连接起来,更全面地表示了数量之间的运算关系。例如,用字母 a 表示一个数是用字母表示数,而\(2a + 3\)则是一个代数式,它表示了这个数的 2 倍与 3 的和。
如何避免在列代数式时出现错误?
列代数式时,要仔细分析数量关系,明确运算顺序。可以先找出关键词,如 “和”“差”“积”“商”“倍”“分”“平方”“立方” 等,确定运算的类型和顺序;同时,要注意代数式的书写规范,避免因书写不规范导致误解。对于复杂的数量关系,可以先分步表示,再组合成一个代数式。
课堂小结
代数式的概念:用运算符号把数或表示数的字母连接而成的式子,单独的一个数或一个字母也是代数式。
代数式的书写规范:包括数与字母、字母与字母相乘的写法,带分数的处理,除法运算的表示,单位的添加等。
代数式的意义:可以从运算角度和实际背景角度进行解释,体现了代数式表示数量关系的一般性和灵活性。
代数式中不含有等号或不等号,这是判断一个式子是否为代数式的重要依据。
课后作业
教材 P59 练习 1、2、3 题。
下列各式中,哪些是代数式?
(1)\(3x + 7\) (2)\(2x - 1 = 6\) (3)\(0\) (4)\(\frac{a + b}{c}\)(\(c 0\)) (5)\(x y\)
用代数式表示:
(1)x 的\(\frac{1}{2}\)与 y 的 3 倍的差;
(2)a、b 两数的和与它们的差的积;
(3)m 的平方与 n 的立方的倒数的和;
(4)比 x 大 10% 的数。
赋予代数式\(4a\)一个实际意义。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.了解代数式的概念,能用代数式表示简单问题中的数量关系;
2.在具体情境中,能求出代数式的值,并解释它的实际意义.
3.通过列代数式,初步体会数学中抽象概括的思维方法.
学习目标
3.图中由长方形和正方形拼成的大正方形的面积为____________;
我们还可以这样想,图中大正方形的边长是_____,因此它的面积是
______.
1.深圳的气温为 x ℃,北京的气温比深圳低4℃,北京的气温为_____℃.
2.深圳到北京的距离是 s km,高铁的速度为 300 km/h,从深圳到北京需_____h.
复习回顾
a +2ab+b
a+b
(a+b)
a
b
a
b
x-4
进行新课
知识点一
代数式的概念及书写方式
观察下列这些式子,它们有何共同特点?
41472n,2k, 2k-1,a+b,(a+b) , , ,
含有数字或字母
含有运算符号
这些式子都是由数、字母用加、减、乘、除及乘方等运算符号连接而成.
1.代数式的概念
41472n,2k, 2k-1,a+b,(a+b) , , ,
像这样用加、减、乘、除及乘方等运算符号把数或表示数的字母连接而成的式子,叫作代数式.
代数式
练一练:下列各式中哪些是代数式?哪些不是?
方法:①代数式中不含表示关系的符号.
(“=”,“>”,“<”,“ ”,“ ”,“≠”)
②单独的一个数或字母也是代数式.
2.代数式的书写方法
(1)练习簿的单价为a元,100本练习簿的总价是______元. b本练习簿的总价是______元.
100a
①若出现乘号,可写成“·”或不写.
数字与字母相乘时,数字写在字母前;
字母与字母相乘时,相同字母写成幂的形式;数字与数字相乘时,乘号“×”不能省略.
ab
(2)某篮球运动员个子高,经测量他通常跨一步的距离1米,若取向前为正,向后为负,那么他向前跨a步为____米,向后跨a步为____米.
a
-a
②当“1”与任何字母相乘时,“1”可省略不写;
当“-1”乘以字母时,只要在那个字母前加上“-”号即可.
(3)若每斤苹果 元,则买m斤苹果需______元.
③带分数与字母相乘时,要将带分数化成假分数.
(4)小明的家离学校 s 千米,小明骑车上学,若每小时行
10千米,则需_____时.
④如果式中出现除法,如s÷v,一般写成 的形式.
(5)练习簿的单价为0.5元,圆珠笔的单价是3.2元,买a本练习簿和b支笔的总价是___________元.
(0.5a+3.2b)
⑤如果式子后面有单位且式子是和或差的形式,式子要用小括号括起来.
练一练:规范下列代数式的书写.
知识点二
列代数式
例
1
用代数式表示:
(1)某商店上月收入x元,本月收入比上月的2倍还多5万元,该商店本月收入为__________元;
(2)一件a元的衬衫,降价10%后,价格为___________元.
列代数式就是把实际问题中的数量关系,用含有数、字母和运算符号的式子表示出来.
2x+50000
(1-10%)a
例
2
用代数式表示:
(1)把a本书分给若干名学生,若每人5本,还剩余3本,求学生数;
解:(1)因为从a本书中去掉3本,按每人5本正好分完,所以学生数为 .
例
2
用代数式表示:
(2)某次高铁列车先以290 km/h的速度运行a h,后以310 km/h的速度运行b h.求它行驶的路程.
解:(2)该次高铁列车行驶的路程为
(290a+310b)km
归纳:列代数式要点
要抓住关键词语,将问题中的数量关系正确地转换为对应的运算.如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
理清语句层次,明确运算顺序;
掌握实际问题中的基本量的关系和公式;
根据运算顺序及与数量关系有关的“的”“与”等字,逐层分析,一步步列出代数式.
1
2
3
4
知识点三
代数式的意义
例
3
说出下列代数式的意义:
(1)如果圆珠笔每支售价a元,练习簿每本售价b元,那么3a+4b表示什么?
(2)如果长方形的长、宽分别为a,b,那么(a+1)b表示什么?
解:(1)3 支圆珠笔与4本练习簿的总金额.
(2)长为a+1、宽为b的长方形的面积.
练一练:说出下列代数式的意义.
(1)m2-n2; (2)7(x+y)(x-y);
(3) ; (4)2x2-3y2.
解:(1)m,n两数的平方差;
(2)x,y两数的和与它们的差的乘积的7倍;
(3)a、b两数的和除以它们的差的商;
(4)x的平方的2倍与y的平方的3倍的差.
随堂演练
1.下列式子:①x÷y;②2m-1个;③-xy2;④mn2.其中格式书写正确的个数是( )A.1 B.2 C.3 D.4
A
2.一件商品的进价是a元,提价30%后出售,则这件商品的售价是( )
A.0.7a 元 B.a 元
C.1.3a 元 D.3a 元
C
【选自教材P65练习 第1题】
3.用代数式表示:
(1)购买单价为a元的贺年卡n张,付出50元,应找回_______元.
(2)女儿今年x岁,妈妈的年龄是女儿的3倍,3年后妈妈的年龄是_______岁.
(3)苹果每千克售价p元,买5kg 以上9折优惠. 现买 15 kg,应付________元.
(4)被3除所得的商为n、余数为2的整数为__________(用n表示).
(50-na)
(3x+3)
13.5p
3n+2
4.用代数式表示:
(1)一桶质量为 m kg的盐水,含盐为 p%,则这桶盐水中水的质量为多少?
(2)某超市一种品牌的矿泉水进价为每瓶a元,零售时每瓶加价20%,每瓶的零售价是多少元?
(3)长方体的长为3m,宽和高都是 a m,则这个长方体的体积是多少?
【选自教材P65~66练习 第2题】
解:(1)(1-p%)m kg.
(2)(1+20%)a 元.
(3)3a2 m3.
5.如图,一组有规律的图案中,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,…,则第n(n是正整数)个图案由多少个基础图形组成?
【选自教材P66练习 第3题】
解:第1个图案中基础图形的个数为 3+1;第2 个图案中基础图形的个数是 3×2+1;第3个图案中基础图形的个数是 3×3+1……所以,第n个图案中基础图形的个数是 3n+1.
1星题 基础练
知识点1 代数式的概念及书写规则
1.下列式子中:;;;; ;
;; ,属于代数式的有( )
A
A.5个 B.6个 C.7个 D.8个
2.下列代数式,表示正确的是( )
C
A. B. C. D. 元
3.下列式子书写不规范,请改正过来.
(1) _____;
(2) ____;
(3) ______;
(4) __.
知识点2 列代数式
4.用代数式表示:
(1)比与 的积的2倍小5的数为_________;
(2)设某工程总量为1,甲单独完成该工程需 天,则甲的工作
效率可以表示为__;
(3)某商品打八折后价格为 元,这件商品的原价为_ ___元.
知识点3 代数式的意义
5.[2024·福州期中]代数式 用语言叙述正确的是
( )
A
A.的平方与 的平方的4倍的和
B.的平方与4的和乘以 的平方
C.与 的和的平方
D.与 的平方和
2星题 中档练
6.数学文化 《九章算术》中记载一问题:“今有共买物,人
出八,盈三;人出七,不足四.问人数、物价各几何?”意思
是:今有若干人合伙购物,每人出8钱,会多 3钱;每人出7
钱,又差4钱.问人数、物价各是多少?设人数为 ,则物价为
( )
D
A.钱 B.钱 C.钱 D. 钱
7.一台“节能电视”成本价为 元,销售价比成本价增加了
,因促销活动,销售价降价 出售,那么每台电视机
的实际售价为____元.
8.[2024·合肥校级一模]将字母“C”,“ ”按照如图所示的
规律摆放,其中第1个图形中有1个字母C,有4个字母 ;第
2个图形中有2个字母C,有6个字母 ;第3个图形中有3个字
母C,有8个字母 根据此规律解答下面的问题:
(1)第4个图形中有___个字母C,有____个字母 ;
4
10
(2)第个图形中有___个字母C,有_________个字母
(用含 的式子表示);
(3)第2 025个图形中有_______个字母C,有_______个字母 .
课堂小结
代数式
概念
应用
用加、减、乘、除及乘方等运算符号把数或表示数的字母连接而成的式子叫作代数式. 单个的数或字母也是代数式.
列代数式
代数式的意义
注意书写规范
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
