2.2.1 合并同类项 课件(共41张PPT)
文档属性
| 名称 | 2.2.1 合并同类项 课件(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 20:47:35 | ||
图片预览









文档简介
(共41张PPT)
2.2.1 合并同类项
第2章 整式及其加减
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
2.2.1 合并同类项
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
上节课我们学习了代数式的值,知道用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果就是代数式的值。同时,我们也掌握了求代数式值的步骤:先代入,再计算。在代数式中,有一类特殊的项,它们具有相同的特征,今天我们就来学习如何处理这些项 —— 合并同类项。
学习目标
理解同类项的概念,能准确判断几个项是否为同类项。
掌握合并同类项的法则,能熟练进行同类项的合并。
经历从具体实例到抽象概念的过程,培养观察、分析和归纳能力。
体会数学的严谨性和简洁性,激发学习数学的兴趣。
课堂导入
在日常生活中,我们经常会对物品进行分类整理,比如把相同的书籍放在一起,把相同的文具放在一起。在数学中,对于多项式中的项,我们也可以按照一定的标准进行分类。观察下面多项式中的项:
\(3x^2 + 2x + 5 - 2x^2 + 3x - 1\)
这些项中,\(3x^2\)与\(-2x^2\)都含有字母 x,且 x 的指数都是 2;\(2x\)与\(3x\)都含有字母 x,且 x 的指数都是 1;\(5\)与\(-1\)都是不含字母的项。我们把这样的项叫做同类项。把同类项合并成一项,就是合并同类项。这节课我们就来学习同类项的概念和合并同类项的方法。
知识点:同类项的概念
定义
所含字母相同,并且相同字母的指数也相同的项叫做同类项。
几个常数项也是同类项。
例如:
同类项:
\(5x\)与\(-3x\)(所含字母都是 x,且 x 的指数都是 1);
\(2a^2b\)与\(-7a^2b\)(所含字母都是 a、b,且 a 的指数都是 2,b 的指数都是 1);
\(3\)与\(-5\)(都是常数项)。
非同类项:
\(2x\)与\(3y\)(所含字母不同);
\(3a^2\)与\(5a^3\)(所含字母相同,但相同字母的指数不同);
\(4ab\)与\(2a^2b\)(所含字母相同,但 a 的指数不同)。
注意事项
同类项与系数无关,与字母的排列顺序无关。例如,\(3xy\)与\(-5yx\)是同类项,因为它们所含字母相同,相同字母的指数也相同,只是字母的排列顺序不同。
判别同类项的标准有两个:一是所含字母相同;二是相同字母的指数也相同,二者缺一不可。
知识点:合并同类项
定义
把多项式中的同类项合并成一项,叫做合并同类项。
例如,在多项式\(3x^2 + 2x + 5 - 2x^2 + 3x - 1\)中,\(3x^2\)与\(-2x^2\)是同类项,可以合并成一项;\(2x\)与\(3x\)是同类项,可以合并成一项;\(5\)与\(-1\)是同类项,可以合并成一项。
法则
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变。
用字母表示为:\(ax^n + bx^n = (a + b)x^n\)(其中 a、b 是系数,n 是正整数)。
例如:
\(3x + 5x = (3 + 5)x = 8x\);
\(-2a^2b + 7a^2b = (-2 + 7)a^2b = 5a^2b\);
\(4 + (-6) = (4 - 6) = -2\)。
知识点:合并同类项的步骤
合并同类项的一般步骤如下:
找出同类项:在多项式中,把同类项用不同的符号标出来,避免遗漏或重复。
移动同类项:利用加法交换律和结合律,把同类项移到一起,移动时要连同项的符号一起移动。
合并同类项:按照合并同类项的法则,将同类项的系数相加,字母和字母的指数不变。
整理结果:合并同类项后,所得的多项式中不再有同类项,一般按某一字母的指数从高到低(或从低到高)的顺序排列。
例如,合并多项式\(3x^2 + 2x + 5 - 2x^2 + 3x - 1\)的同类项:
找出同类项:\(3x^2\)与\(-2x^2\),\(2x\)与\(3x\),\(5\)与\(-1\);
移动同类项:\(3x^2 - 2x^2 + 2x + 3x + 5 - 1\);
合并同类项:\((3 - 2)x^2 + (2 + 3)x + (5 - 1) = x^2 + 5x + 4\);
整理结果:\(x^2 + 5x + 4\)(按 x 的指数从高到低排列)。
例题解析
例 1:判断下列各组中的项是不是同类项,为什么?
(1)\(2x^2y\)与\(-3x^2y\);
(2)\(5ab\)与\(5a\);
(3)\(-7\)与\(\frac{1}{3}\);
(4)\(4m^2n\)与\(2mn^2\)。
解:(1)是同类项。因为它们所含字母相同(都是 x、y),且相同字母的指数也相同(x 的指数都是 2,y 的指数都是 1)。
(2)不是同类项。因为它们所含字母不同(5ab 含字母 a、b,5a 含字母 a)。
(3)是同类项。因为它们都是常数项。
(4)不是同类项。因为它们所含字母相同,但相同字母的指数不同(4m n 中 m 的指数是 2,n 的指数是 1;2mn 中 m 的指数是 1,n 的指数是 2)。
例 2:合并下列多项式中的同类项:
(1)\(4x^2 - 8x + 5 - 3x^2 + 6x - 2\);
(2)\(3a^2 + 2ab - 5a^2 + b^2 - 2ab + 3b^2\)。
解:(1)\(
\begin{align*}
&4x^2 - 8x + 5 - 3x^2 + 6x - 2\\
=&(4x^2 - 3x^2) + (-8x + 6x) + (5 - 2)\\
=&(4 - 3)x^2 + (-8 + 6)x + 3\\
=&x^2 - 2x + 3
\end{align*}
\)
(2)\(
\begin{align*}
&3a^2 + 2ab - 5a^2 + b^2 - 2ab + 3b^2\\
=&(3a^2 - 5a^2) + (2ab - 2ab) + (b^2 + 3b^2)\\
=&(3 - 5)a^2 + (2 - 2)ab + (1 + 3)b^2\\
=&-2a^2 + 4b^2
\end{align*}
\)
例 3:求多项式\(3x^2 - 4x + 5 - 2x^2 + x - 1\)的值,其中\(x = -2\)。
解:先合并同类项,再代入求值:\(
\begin{align*}
&3x^2 - 4x + 5 - 2x^2 + x - 1\\
=&(3x^2 - 2x^2) + (-4x + x) + (5 - 1)\\
=&x^2 - 3x + 4
\end{align*}
\)
当\(x = -2\)时,\(
\begin{align*}
&(-2)^2 - 3 (-2) + 4\\
=&4 + 6 + 4\\
=&14
\end{align*}
\)
例 4:如果\(2x^3y^m\)与\(-3x^ny^2\)是同类项,求 m、n 的值。
解:因为\(2x^3y^m\)与\(-3x^ny^2\)是同类项,根据同类项的定义,所含字母相同,并且相同字母的指数也相同,所以:\(n = 3\),\(m = 2\)。
小练习
判断下列各组中的项是不是同类项:
(1)\(3x\)与\(3y\);
(2)\(-5a^2b\)与\(2ba^2\);
(3)\(4\)与\(-6\);
(4)\(3x^2\)与\(2x^3\)。
合并下列多项式中的同类项:
(1)\(5a + 4b - 3a - 7b\);
(2)\(x^2y - 3xy^2 + 2yx^2 - y^2x\);
(3)\(3x^2 - 1 - 2x - 5 + 3x - x^2\)。
求下列多项式的值:
(1)\(5x^2 - 3x^3 - x - 4 + 2x^3 + 2x + x^3 - 9\),其中\(x = -1\);
(2)\(3a + abc - \frac{1}{3}c^2 - 3a + \frac{1}{3}c^2\),其中\(a = -\frac{1}{6}\),\(b = 2\),\(c = -3\)。
填空:
(1)若\(3x^ky\)与\(-x^2y\)是同类项,则\(k = \)。
(2)合并同类项:\(-p^2 - p^2 - p^2 = \)。
(3)多项式\(2x^2 + ax - y + 6\)与\(2bx^2 - 3x + 5y - 1\)的差中不含 x 项和 x 项,则\(a = \),\(b = \)。
思考讨论
同类项与系数有关吗?与字母的排列顺序有关吗?
同类项与系数无关,与字母的排列顺序也无关。判断几个项是否为同类项,只看所含字母是否相同和相同字母的指数是否相同,只要这两个条件满足,无论系数是否相同、字母的排列顺序如何,都是同类项。例如,\(5xy\)与\(-3yx\)是同类项,虽然系数不同,字母的排列顺序也不同,但所含字母相同,相同字母的指数也相同。
合并同类项的依据是什么?
合并同类项的依据是乘法分配律的逆运用。例如,合并\(3x + 5x\)时,根据乘法分配律\(ac + bc = (a + b)c\),可得\(3x + 5x = (3 + 5)x = 8x\)。
课堂小结
同类项的概念:所含字母相同,并且相同字母的指数也相同的项,几个常数项也是同类项。
合并同类项的法则:同类项的系数相加,所得的结果作为系数,字母和字母的指数不变。
合并同类项的步骤:找出同类项→移动同类项→合并同类项→整理结果。
合并同类项可以使多项式变得更简洁,便于进一步的运算和求值。
课后作业
教材 P69 练习 1、2、3、4 题。
合并下列多项式中的同类项:
(1)\(6a^2b + 5ab^2 - 4ab^2 - 7a^2b\);
(2)\(4a^2 + 3b^2 + 2ab - 4a^2 - 4b^2\);
(3)\(3x^2 - [7x - (4x - 3) - 2x^2]\)。
求下列多项式的值:
(1)\(3x^2y^2 + 2xy - 7x^2y^2 - \frac{3}{2}xy + 2 + 4x^2y^2\),其中\(x = 2\),\(y = -\frac{1}{4}\);
(2)\(2(a^2b + ab^2) - 2(a^2b - 1) - 2ab^2 - 2\),其中\(a = -2\),\(b = 2\)。
若多项式\(x^4 - (a - 1)x^3 + 5x^2 - (b + 3)x - 1\)中不含 x 项和 x 项,求 a、b 的值。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解同类项、合并同类项的概念及合并同类项的法则.
2.能运用合并同类项的法则进行同类项的合并以及多项式的化简与求值.
3.通过类比数的运算法则探究合并同类项的法则,体会类比的数学思想.
学习目标
复习回顾
除系数不同外,字母部分相同.
1.观察:式子 a与4a,ab与 ab有什么特点?
2.计算: 用到了什么运算定律?2a+3b=5ab呢?
分配律;
思考:什么样的式子才可以合并?
2a+3b≠5ab
进行新课
知识点一
同类项的概念
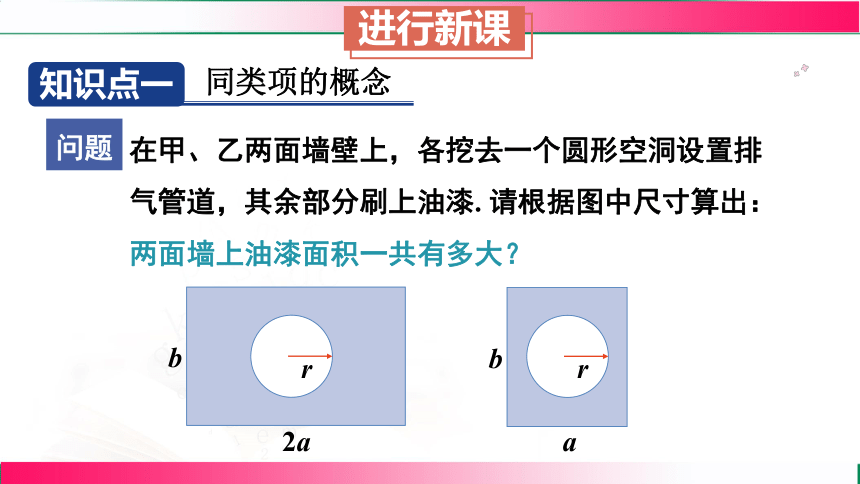
问题
在甲、乙两面墙壁上,各挖去一个圆形空洞设置排气管道,其余部分刷上油漆. 请根据图中尺寸算出:两面墙上油漆面积一共有多大?
b
2a
r
b
a
r
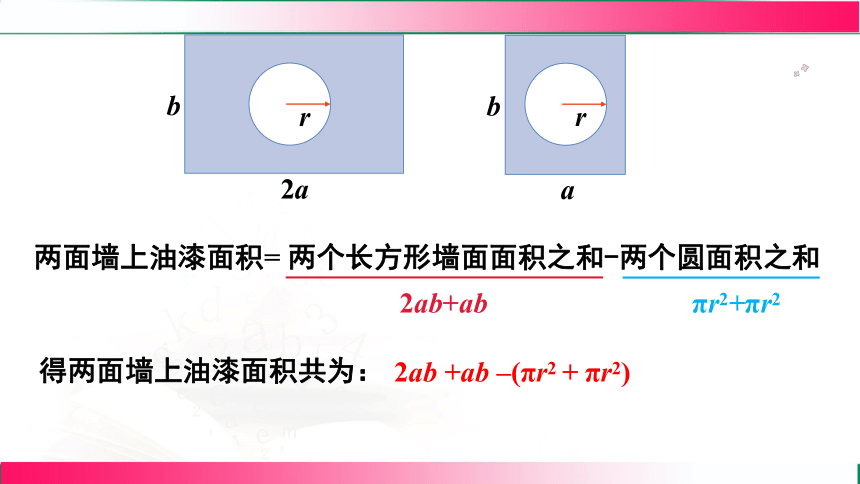
两面墙上油漆面积= 两个长方形墙面面积之和-两个圆面积之和
2ab+ab
πr2+πr2
得两面墙上油漆面积共为:
2ab +ab –(πr2 + πr2)
b
2a
r
b
a
r
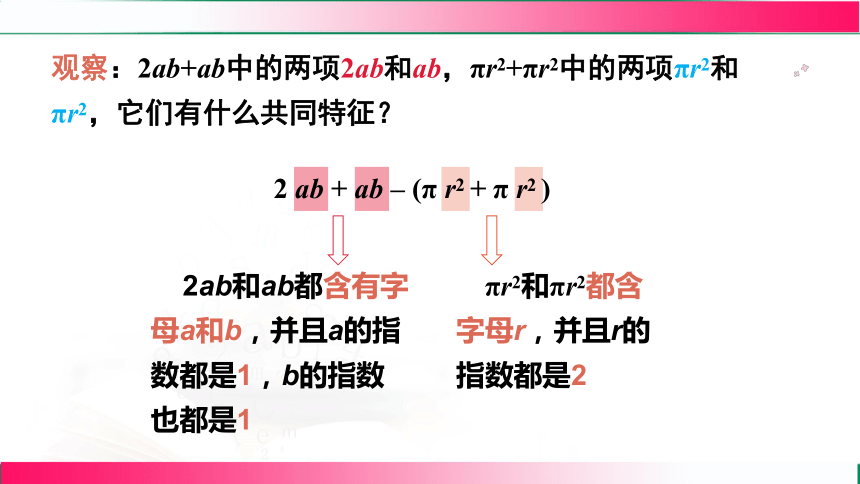
观察:2ab+ab中的两项2ab和ab,πr2+πr2中的两项πr2和πr2,它们有什么共同特征?
2 ab + ab – (π r2 + π r2 )
2ab和ab都含有字母a和b,并且a的指数都是1,b的指数也都是1
πr2和πr2都含字母r,并且r的指数都是2
2 ab + ab – (π r2 + π r2 )
常数项与常数项是同类项
像这样,所含字母相同,并且相同字母的指数也分别相同的项叫作同类项.
练一练:下列各组式子中,是同类项的是( )
A.①②③ B.①③④⑥ C.③⑤⑥ D.只有⑥
C
【分析】字母相同:① ③ ⑤
相同字母的指数相同:③ ⑤
都是常数项:⑥
两“相同”
①所含字母相同;
②相同字母的指数分别相同.
两“无关”
①与系数的大小无关;
②与它们所含字母的顺序无关.
归纳:怎样判断同类项?
一“特例”
常数项都是同类项
知识点二
合并同类项
在多项式中遇到同类项,可以运用加法交换律、加法结合律、分配律进行合并.
=4x2-3x2+2x+3x-1+2
=(4-3)x2+(2+3)x+(-1+2)
=x2+5x+1
4x2+2x -1 -3x2+3x+2
移
组
=(4x2-3x2)+(2x+3x)+[(-1)+2]
并
加法交换律
加法结合律
分配律
算
找
合并同类项:
把多项式中的同类项合并成一项,叫作合并同类项.
合并同类项的法则:
同类项的系数相加,所得结果作为系数,字母和字母的指数不变.
合并同类项:
例
1
(1)4a2+3b2-2ab-3a2+b2;
解:(1) 4a2+3b2-2ab-3a2+b2
= 4a2-3a2-2ab+3b2+b2
= (4-3)a2-2ab+(3+1)b2
= a2-2ab+4b2
合并同类项:
例
1
合并同类项的方法:
“找”:找出多项式中的同类项,不同类的同类项用不同的标记标出;
“移”:利用加法的交换律和结合律把同类项放在一起,在交换位置时,连同项的符号一起交换;
“并”:利用合并同类项的法则合并同类项,即将系数相加,而字母与其指数不变.
1
2
3
随堂演练
【选自教材P76练习 第1题】
1.下列各题中的两项是不是同类项?
(1)3a2b与3ab2; (2)xy与-xy;
(2)4abc与4ac; (4)-3与
不是
不是
是
是
2.下列运算正确的是( )
A. 3a+2b=5ab
B. 3a2b-3ba2=0
C. 3x2+2x3=5x5
D. 5y2-4y2=1
B
3.下列合并同类项的结果是否正确?若不正确,请给出正确结果.
(1)5x2+6x2=11x4; (2)5x+2x=7x2;
(3)5x2-3x2=2; (4)16xy-16yx=0.
解:(1)错误, 5x2+6x2=11x2.
(2)错误, 5x+2x=7x.
(3)错误, 5x2-3x2=2x2.
(4)正确.
【选自教材P76练习 第2题】
4.合并同类项:
(1)-8x+8x=_______;(2)-a-7a+3a=_______;
(3) =_______;
(4) =_______.
0
0
-5a
【选自教材P76练习 第3题】
5.已知 -4xaya+1 与 mx5yb-1 的和是 3x5yn,求(m-n)(2a-b)的值.
解:因为-4xaya+1与mx5yb-1的和是3x5yn,
所以-4+m=3,a=5,a+1=b-1=n.
所以a=5,b=7,m=7,n=6.
所以(m-n)(2a-b)=(7-6)×(2×5-7)=3.
1星题 基础练
知识点1 同类项
1.下列整式中,与 是同类项的是( )
D
A.2 B. C. D.
2.教材改编题下列各组中的两个式子不属于同类项的是
( )
D
A.和 B.和
C.和 D.和
3.若单项式和是同类项,则 的值为___.
4
4.在中, 与_____是同类项,
与_____是同类项, 与___是同类项.
1
知识点2 合并同类项
5.[知识初练]合并同类项:
(1)______ ;
(2)(___-___) .
2
6
2
3
6.[2024·合肥蜀山区期中]下列计算正确的是( )
C
A. B.
C. D.
7.(12分)化简:
(1) ;
解:原式
.
(2) ;
解:原式
.
(3) .
解:原式 .
8.(8分)先化简,再求值:
.其中 ,
.
解:原式 .
当,时,原式 .
2星题 中档练
9.一个五次六项式加上一个五次三项式,合并同类项后一定
是( )
D
A.十次九项式 B.五次六项式
C.五次九项式 D.不超过五次的整式
10.若与的和为单项式,则 的值是____.
11.易错题 若关于, 的多项式
中不含项,则 的值是____.
12.整体思想 已知,,则 的
值为____.
15
13.[2025·天津模拟]如图所示的月
历中,带阴影的方框里有四个数,随
着方框的移动,方框里的四个数存在
一定的关系.设方框里最小的一个数为
,则这四个数之和为_________
(用含 的代数式表示,并化为最简).
14.创新题·新考法 [2024·江苏淮安期中] 类比同类项的概念,
我们规定:所含字母相同,并且相同字母的指数之差的绝对
值等于0或1的项是“准同类项”,例如:与 是“准
同类项”.已知、均为关于, 的单项式,如果
、是“准同类项”,那么 可能的结果共有
___种.
5
15.(8分)已知代数式
的值与字母 的取
值无关,求 的值.
解:原式 ,
因为结果与字母 的取值无关,
所以, ,
解得, ,
则 .
3星题 提升练
16.(12分)运算能力 我们知道 ,类
似地,我们把 看成一个整体,则
.“整体思
想”是中学数学解题中常用的一种重要的思想方法,它在多
项式的化简与求值中应用比较广泛,请尝试应用“整体思想”
解答下列问题.
(1)把 看成一个整体,合并同类项:
___________;
(2)化简: ;
解:原式 .
(3)若,,求 的值.
因为,,所以 .
课堂小结
同类项的概念
合并同类项
同类项的判断
合并同类项
两“相同”、两“无关”、一“特例”
同类项的系数相加,所得结果作为系数,字母和字母的指数不变.
所含字母相同,并且相同字母的指数也分别相同
谢谢观看!
2.2.1 合并同类项
第2章 整式及其加减
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
2.2.1 合并同类项
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
上节课我们学习了代数式的值,知道用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果就是代数式的值。同时,我们也掌握了求代数式值的步骤:先代入,再计算。在代数式中,有一类特殊的项,它们具有相同的特征,今天我们就来学习如何处理这些项 —— 合并同类项。
学习目标
理解同类项的概念,能准确判断几个项是否为同类项。
掌握合并同类项的法则,能熟练进行同类项的合并。
经历从具体实例到抽象概念的过程,培养观察、分析和归纳能力。
体会数学的严谨性和简洁性,激发学习数学的兴趣。
课堂导入
在日常生活中,我们经常会对物品进行分类整理,比如把相同的书籍放在一起,把相同的文具放在一起。在数学中,对于多项式中的项,我们也可以按照一定的标准进行分类。观察下面多项式中的项:
\(3x^2 + 2x + 5 - 2x^2 + 3x - 1\)
这些项中,\(3x^2\)与\(-2x^2\)都含有字母 x,且 x 的指数都是 2;\(2x\)与\(3x\)都含有字母 x,且 x 的指数都是 1;\(5\)与\(-1\)都是不含字母的项。我们把这样的项叫做同类项。把同类项合并成一项,就是合并同类项。这节课我们就来学习同类项的概念和合并同类项的方法。
知识点:同类项的概念
定义
所含字母相同,并且相同字母的指数也相同的项叫做同类项。
几个常数项也是同类项。
例如:
同类项:
\(5x\)与\(-3x\)(所含字母都是 x,且 x 的指数都是 1);
\(2a^2b\)与\(-7a^2b\)(所含字母都是 a、b,且 a 的指数都是 2,b 的指数都是 1);
\(3\)与\(-5\)(都是常数项)。
非同类项:
\(2x\)与\(3y\)(所含字母不同);
\(3a^2\)与\(5a^3\)(所含字母相同,但相同字母的指数不同);
\(4ab\)与\(2a^2b\)(所含字母相同,但 a 的指数不同)。
注意事项
同类项与系数无关,与字母的排列顺序无关。例如,\(3xy\)与\(-5yx\)是同类项,因为它们所含字母相同,相同字母的指数也相同,只是字母的排列顺序不同。
判别同类项的标准有两个:一是所含字母相同;二是相同字母的指数也相同,二者缺一不可。
知识点:合并同类项
定义
把多项式中的同类项合并成一项,叫做合并同类项。
例如,在多项式\(3x^2 + 2x + 5 - 2x^2 + 3x - 1\)中,\(3x^2\)与\(-2x^2\)是同类项,可以合并成一项;\(2x\)与\(3x\)是同类项,可以合并成一项;\(5\)与\(-1\)是同类项,可以合并成一项。
法则
合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变。
用字母表示为:\(ax^n + bx^n = (a + b)x^n\)(其中 a、b 是系数,n 是正整数)。
例如:
\(3x + 5x = (3 + 5)x = 8x\);
\(-2a^2b + 7a^2b = (-2 + 7)a^2b = 5a^2b\);
\(4 + (-6) = (4 - 6) = -2\)。
知识点:合并同类项的步骤
合并同类项的一般步骤如下:
找出同类项:在多项式中,把同类项用不同的符号标出来,避免遗漏或重复。
移动同类项:利用加法交换律和结合律,把同类项移到一起,移动时要连同项的符号一起移动。
合并同类项:按照合并同类项的法则,将同类项的系数相加,字母和字母的指数不变。
整理结果:合并同类项后,所得的多项式中不再有同类项,一般按某一字母的指数从高到低(或从低到高)的顺序排列。
例如,合并多项式\(3x^2 + 2x + 5 - 2x^2 + 3x - 1\)的同类项:
找出同类项:\(3x^2\)与\(-2x^2\),\(2x\)与\(3x\),\(5\)与\(-1\);
移动同类项:\(3x^2 - 2x^2 + 2x + 3x + 5 - 1\);
合并同类项:\((3 - 2)x^2 + (2 + 3)x + (5 - 1) = x^2 + 5x + 4\);
整理结果:\(x^2 + 5x + 4\)(按 x 的指数从高到低排列)。
例题解析
例 1:判断下列各组中的项是不是同类项,为什么?
(1)\(2x^2y\)与\(-3x^2y\);
(2)\(5ab\)与\(5a\);
(3)\(-7\)与\(\frac{1}{3}\);
(4)\(4m^2n\)与\(2mn^2\)。
解:(1)是同类项。因为它们所含字母相同(都是 x、y),且相同字母的指数也相同(x 的指数都是 2,y 的指数都是 1)。
(2)不是同类项。因为它们所含字母不同(5ab 含字母 a、b,5a 含字母 a)。
(3)是同类项。因为它们都是常数项。
(4)不是同类项。因为它们所含字母相同,但相同字母的指数不同(4m n 中 m 的指数是 2,n 的指数是 1;2mn 中 m 的指数是 1,n 的指数是 2)。
例 2:合并下列多项式中的同类项:
(1)\(4x^2 - 8x + 5 - 3x^2 + 6x - 2\);
(2)\(3a^2 + 2ab - 5a^2 + b^2 - 2ab + 3b^2\)。
解:(1)\(
\begin{align*}
&4x^2 - 8x + 5 - 3x^2 + 6x - 2\\
=&(4x^2 - 3x^2) + (-8x + 6x) + (5 - 2)\\
=&(4 - 3)x^2 + (-8 + 6)x + 3\\
=&x^2 - 2x + 3
\end{align*}
\)
(2)\(
\begin{align*}
&3a^2 + 2ab - 5a^2 + b^2 - 2ab + 3b^2\\
=&(3a^2 - 5a^2) + (2ab - 2ab) + (b^2 + 3b^2)\\
=&(3 - 5)a^2 + (2 - 2)ab + (1 + 3)b^2\\
=&-2a^2 + 4b^2
\end{align*}
\)
例 3:求多项式\(3x^2 - 4x + 5 - 2x^2 + x - 1\)的值,其中\(x = -2\)。
解:先合并同类项,再代入求值:\(
\begin{align*}
&3x^2 - 4x + 5 - 2x^2 + x - 1\\
=&(3x^2 - 2x^2) + (-4x + x) + (5 - 1)\\
=&x^2 - 3x + 4
\end{align*}
\)
当\(x = -2\)时,\(
\begin{align*}
&(-2)^2 - 3 (-2) + 4\\
=&4 + 6 + 4\\
=&14
\end{align*}
\)
例 4:如果\(2x^3y^m\)与\(-3x^ny^2\)是同类项,求 m、n 的值。
解:因为\(2x^3y^m\)与\(-3x^ny^2\)是同类项,根据同类项的定义,所含字母相同,并且相同字母的指数也相同,所以:\(n = 3\),\(m = 2\)。
小练习
判断下列各组中的项是不是同类项:
(1)\(3x\)与\(3y\);
(2)\(-5a^2b\)与\(2ba^2\);
(3)\(4\)与\(-6\);
(4)\(3x^2\)与\(2x^3\)。
合并下列多项式中的同类项:
(1)\(5a + 4b - 3a - 7b\);
(2)\(x^2y - 3xy^2 + 2yx^2 - y^2x\);
(3)\(3x^2 - 1 - 2x - 5 + 3x - x^2\)。
求下列多项式的值:
(1)\(5x^2 - 3x^3 - x - 4 + 2x^3 + 2x + x^3 - 9\),其中\(x = -1\);
(2)\(3a + abc - \frac{1}{3}c^2 - 3a + \frac{1}{3}c^2\),其中\(a = -\frac{1}{6}\),\(b = 2\),\(c = -3\)。
填空:
(1)若\(3x^ky\)与\(-x^2y\)是同类项,则\(k = \)。
(2)合并同类项:\(-p^2 - p^2 - p^2 = \)。
(3)多项式\(2x^2 + ax - y + 6\)与\(2bx^2 - 3x + 5y - 1\)的差中不含 x 项和 x 项,则\(a = \),\(b = \)。
思考讨论
同类项与系数有关吗?与字母的排列顺序有关吗?
同类项与系数无关,与字母的排列顺序也无关。判断几个项是否为同类项,只看所含字母是否相同和相同字母的指数是否相同,只要这两个条件满足,无论系数是否相同、字母的排列顺序如何,都是同类项。例如,\(5xy\)与\(-3yx\)是同类项,虽然系数不同,字母的排列顺序也不同,但所含字母相同,相同字母的指数也相同。
合并同类项的依据是什么?
合并同类项的依据是乘法分配律的逆运用。例如,合并\(3x + 5x\)时,根据乘法分配律\(ac + bc = (a + b)c\),可得\(3x + 5x = (3 + 5)x = 8x\)。
课堂小结
同类项的概念:所含字母相同,并且相同字母的指数也相同的项,几个常数项也是同类项。
合并同类项的法则:同类项的系数相加,所得的结果作为系数,字母和字母的指数不变。
合并同类项的步骤:找出同类项→移动同类项→合并同类项→整理结果。
合并同类项可以使多项式变得更简洁,便于进一步的运算和求值。
课后作业
教材 P69 练习 1、2、3、4 题。
合并下列多项式中的同类项:
(1)\(6a^2b + 5ab^2 - 4ab^2 - 7a^2b\);
(2)\(4a^2 + 3b^2 + 2ab - 4a^2 - 4b^2\);
(3)\(3x^2 - [7x - (4x - 3) - 2x^2]\)。
求下列多项式的值:
(1)\(3x^2y^2 + 2xy - 7x^2y^2 - \frac{3}{2}xy + 2 + 4x^2y^2\),其中\(x = 2\),\(y = -\frac{1}{4}\);
(2)\(2(a^2b + ab^2) - 2(a^2b - 1) - 2ab^2 - 2\),其中\(a = -2\),\(b = 2\)。
若多项式\(x^4 - (a - 1)x^3 + 5x^2 - (b + 3)x - 1\)中不含 x 项和 x 项,求 a、b 的值。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解同类项、合并同类项的概念及合并同类项的法则.
2.能运用合并同类项的法则进行同类项的合并以及多项式的化简与求值.
3.通过类比数的运算法则探究合并同类项的法则,体会类比的数学思想.
学习目标
复习回顾
除系数不同外,字母部分相同.
1.观察:式子 a与4a,ab与 ab有什么特点?
2.计算: 用到了什么运算定律?2a+3b=5ab呢?
分配律;
思考:什么样的式子才可以合并?
2a+3b≠5ab
进行新课
知识点一
同类项的概念
问题
在甲、乙两面墙壁上,各挖去一个圆形空洞设置排气管道,其余部分刷上油漆. 请根据图中尺寸算出:两面墙上油漆面积一共有多大?
b
2a
r
b
a
r
两面墙上油漆面积= 两个长方形墙面面积之和-两个圆面积之和
2ab+ab
πr2+πr2
得两面墙上油漆面积共为:
2ab +ab –(πr2 + πr2)
b
2a
r
b
a
r
观察:2ab+ab中的两项2ab和ab,πr2+πr2中的两项πr2和πr2,它们有什么共同特征?
2 ab + ab – (π r2 + π r2 )
2ab和ab都含有字母a和b,并且a的指数都是1,b的指数也都是1
πr2和πr2都含字母r,并且r的指数都是2
2 ab + ab – (π r2 + π r2 )
常数项与常数项是同类项
像这样,所含字母相同,并且相同字母的指数也分别相同的项叫作同类项.
练一练:下列各组式子中,是同类项的是( )
A.①②③ B.①③④⑥ C.③⑤⑥ D.只有⑥
C
【分析】字母相同:① ③ ⑤
相同字母的指数相同:③ ⑤
都是常数项:⑥
两“相同”
①所含字母相同;
②相同字母的指数分别相同.
两“无关”
①与系数的大小无关;
②与它们所含字母的顺序无关.
归纳:怎样判断同类项?
一“特例”
常数项都是同类项
知识点二
合并同类项
在多项式中遇到同类项,可以运用加法交换律、加法结合律、分配律进行合并.
=4x2-3x2+2x+3x-1+2
=(4-3)x2+(2+3)x+(-1+2)
=x2+5x+1
4x2+2x -1 -3x2+3x+2
移
组
=(4x2-3x2)+(2x+3x)+[(-1)+2]
并
加法交换律
加法结合律
分配律
算
找
合并同类项:
把多项式中的同类项合并成一项,叫作合并同类项.
合并同类项的法则:
同类项的系数相加,所得结果作为系数,字母和字母的指数不变.
合并同类项:
例
1
(1)4a2+3b2-2ab-3a2+b2;
解:(1) 4a2+3b2-2ab-3a2+b2
= 4a2-3a2-2ab+3b2+b2
= (4-3)a2-2ab+(3+1)b2
= a2-2ab+4b2
合并同类项:
例
1
合并同类项的方法:
“找”:找出多项式中的同类项,不同类的同类项用不同的标记标出;
“移”:利用加法的交换律和结合律把同类项放在一起,在交换位置时,连同项的符号一起交换;
“并”:利用合并同类项的法则合并同类项,即将系数相加,而字母与其指数不变.
1
2
3
随堂演练
【选自教材P76练习 第1题】
1.下列各题中的两项是不是同类项?
(1)3a2b与3ab2; (2)xy与-xy;
(2)4abc与4ac; (4)-3与
不是
不是
是
是
2.下列运算正确的是( )
A. 3a+2b=5ab
B. 3a2b-3ba2=0
C. 3x2+2x3=5x5
D. 5y2-4y2=1
B
3.下列合并同类项的结果是否正确?若不正确,请给出正确结果.
(1)5x2+6x2=11x4; (2)5x+2x=7x2;
(3)5x2-3x2=2; (4)16xy-16yx=0.
解:(1)错误, 5x2+6x2=11x2.
(2)错误, 5x+2x=7x.
(3)错误, 5x2-3x2=2x2.
(4)正确.
【选自教材P76练习 第2题】
4.合并同类项:
(1)-8x+8x=_______;(2)-a-7a+3a=_______;
(3) =_______;
(4) =_______.
0
0
-5a
【选自教材P76练习 第3题】
5.已知 -4xaya+1 与 mx5yb-1 的和是 3x5yn,求(m-n)(2a-b)的值.
解:因为-4xaya+1与mx5yb-1的和是3x5yn,
所以-4+m=3,a=5,a+1=b-1=n.
所以a=5,b=7,m=7,n=6.
所以(m-n)(2a-b)=(7-6)×(2×5-7)=3.
1星题 基础练
知识点1 同类项
1.下列整式中,与 是同类项的是( )
D
A.2 B. C. D.
2.教材改编题下列各组中的两个式子不属于同类项的是
( )
D
A.和 B.和
C.和 D.和
3.若单项式和是同类项,则 的值为___.
4
4.在中, 与_____是同类项,
与_____是同类项, 与___是同类项.
1
知识点2 合并同类项
5.[知识初练]合并同类项:
(1)______ ;
(2)(___-___) .
2
6
2
3
6.[2024·合肥蜀山区期中]下列计算正确的是( )
C
A. B.
C. D.
7.(12分)化简:
(1) ;
解:原式
.
(2) ;
解:原式
.
(3) .
解:原式 .
8.(8分)先化简,再求值:
.其中 ,
.
解:原式 .
当,时,原式 .
2星题 中档练
9.一个五次六项式加上一个五次三项式,合并同类项后一定
是( )
D
A.十次九项式 B.五次六项式
C.五次九项式 D.不超过五次的整式
10.若与的和为单项式,则 的值是____.
11.易错题 若关于, 的多项式
中不含项,则 的值是____.
12.整体思想 已知,,则 的
值为____.
15
13.[2025·天津模拟]如图所示的月
历中,带阴影的方框里有四个数,随
着方框的移动,方框里的四个数存在
一定的关系.设方框里最小的一个数为
,则这四个数之和为_________
(用含 的代数式表示,并化为最简).
14.创新题·新考法 [2024·江苏淮安期中] 类比同类项的概念,
我们规定:所含字母相同,并且相同字母的指数之差的绝对
值等于0或1的项是“准同类项”,例如:与 是“准
同类项”.已知、均为关于, 的单项式,如果
、是“准同类项”,那么 可能的结果共有
___种.
5
15.(8分)已知代数式
的值与字母 的取
值无关,求 的值.
解:原式 ,
因为结果与字母 的取值无关,
所以, ,
解得, ,
则 .
3星题 提升练
16.(12分)运算能力 我们知道 ,类
似地,我们把 看成一个整体,则
.“整体思
想”是中学数学解题中常用的一种重要的思想方法,它在多
项式的化简与求值中应用比较广泛,请尝试应用“整体思想”
解答下列问题.
(1)把 看成一个整体,合并同类项:
___________;
(2)化简: ;
解:原式 .
(3)若,,求 的值.
因为,,所以 .
课堂小结
同类项的概念
合并同类项
同类项的判断
合并同类项
两“相同”、两“无关”、一“特例”
同类项的系数相加,所得结果作为系数,字母和字母的指数不变.
所含字母相同,并且相同字母的指数也分别相同
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
