2.2.3 整式加减 课件(共40张PPT)
文档属性
| 名称 | 2.2.3 整式加减 课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览











文档简介
(共40张PPT)
2.2.3 整式加减
第2章 整式及其加减
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
2.2.3 整式加减
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
前面我们学习了同类项、合并同类项以及去括号和添括号的知识。合并同类项是把多项式中的同类项合并成一项;去括号和添括号是代数式变形的重要方法,它们都遵循一定的法则。今天我们要学习的整式加减,就是以这些知识为基础进行的运算。
学习目标
理解整式加减的意义,知道整式加减的实质是去括号和合并同类项。
能熟练进行整式的加减运算,包括整式的加法和减法。
能运用整式加减解决实际问题,提高分析和解决问题的能力。
感受整式加减在数学中的应用,体会数学的逻辑性和严谨性。
课堂导入
我们来看一个问题:一个长方形的长为\((3x + 2y)\)厘米,宽为\((x - y)\)厘米,那么这个长方形的周长是多少厘米呢?
长方形的周长公式是\(2 (é + )\),所以这个长方形的周长可以表示为\(2[(3x + 2y)+(x - y)]\)厘米。要算出这个结果,我们需要先去掉括号,再合并同类项,这就是整式的加减运算。通过今天的学习,我们就能轻松解决这类问题。
知识点:整式加减的意义
整式的加减就是求几个整式的和或差的运算。它的实质是运用去括号法则和合并同类项法则,将整式化简为一个最简整式(即不含同类项的整式)。
例如:
求整式\(3x + 2y\)与\(x - y\)的和,就是进行整式的加法运算,可表示为\((3x + 2y)+(x - y)\)。
求整式\(5a^2 - 3b^2\)与\(2a^2 + b^2\)的差,就是进行整式的减法运算,可表示为\((5a^2 - 3b^2)-(2a^2 + b^2)\)。
知识点:整式加减的步骤
整式加减的一般步骤如下:
去括号:如果整式加减运算中有括号,要先根据去括号法则去掉括号。如果括号前面是 “+” 号,去掉括号后,括号内的各项符号不变;如果括号前面是 “-” 号,去掉括号后,括号内的各项符号都要改变。
合并同类项:去掉括号后,按照合并同类项的法则,把多项式中的同类项合并成一项,使结果化为最简整式。
例如,计算\((3x + 2y)+(x - y)\):
去括号:\(3x + 2y + x - y\);
合并同类项:\((3x + x)+(2y - y)=4x + y\)。
再如,计算\((5a^2 - 3b^2)-(2a^2 + b^2)\):
去括号:\(5a^2 - 3b^2 - 2a^2 - b^2\);
合并同类项:\((5a^2 - 2a^2)+(-3b^2 - b^2)=3a^2 - 4b^2\)。
例题解析
例 1:计算:
(1)\((2x^2 + 3x - 1)+(x^2 - 2x + 5)\);
(2)\((4a^2b - 3ab^2)-(2a^2b - 5ab^2)\);
(3)\(3(x^2 - 2xy + y^2)-2(x^2 - xy + y^2)\)。
解:(1)\(
\begin{align*}
&(2x^2 + 3x - 1)+(x^2 - 2x + 5)\\
=&2x^2 + 3x - 1 + x^2 - 2x + 5\\
=&(2x^2 + x^2)+(3x - 2x)+(-1 + 5)\\
=&3x^2 + x + 4
\end{align*}
\)
(2)\(
\begin{align*}
&(4a^2b - 3ab^2)-(2a^2b - 5ab^2)\\
=&4a^2b - 3ab^2 - 2a^2b + 5ab^2\\
=&(4a^2b - 2a^2b)+(-3ab^2 + 5ab^2)\\
=&2a^2b + 2ab^2
\end{align*}
\)
(3)\(
\begin{align*}
&3(x^2 - 2xy + y^2)-2(x^2 - xy + y^2)\\
=&3x^2 - 6xy + 3y^2 - 2x^2 + 2xy - 2y^2\\
=&(3x^2 - 2x^2)+(-6xy + 2xy)+(3y^2 - 2y^2)\\
=&x^2 - 4xy + y^2
\end{align*}
\)
例 2:先化简,再求值:
(1)\((5x^2 - 3y^2)-(5x^2 + 3y^2)\),其中\(x = 1\),\(y = -1\);
(2)\(2(2a + b)^2 - 3(2a + b)+8(2a + b)^2 - 6(2a + b)\),其中\(a = -\frac{3}{4}\),\(b = \frac{1}{2}\)。
解:(1)先化简:\(
\begin{align*}
&(5x^2 - 3y^2)-(5x^2 + 3y^2)\\
=&5x^2 - 3y^2 - 5x^2 - 3y^2\\
=&-6y^2
\end{align*}
\)
当\(x = 1\),\(y = -1\)时,代入得:\(-6 (-1)^2=-6 1 = -6\)
(2)先化简,把\((2a + b)\)看作一个整体合并同类项:\(
\begin{align*}
&2(2a + b)^2 - 3(2a + b)+8(2a + b)^2 - 6(2a + b)\\
=&(2 + 8)(2a + b)^2+(-3 - 6)(2a + b)\\
=&10(2a + b)^2 - 9(2a + b)
\end{align*}
\)
当\(a = -\frac{3}{4}\),\(b = \frac{1}{2}\)时,计算\(2a + b\):\(2 (-\frac{3}{4})+\frac{1}{2}=-\frac{3}{2}+\frac{1}{2}=-1\)
把\(2a + b=-1\)代入化简后的式子得:\(
\begin{align*}
&10 (-1)^2 - 9 (-1)\\
=&10 1 + 9\\
=&19
\end{align*}
\)
例 3:已知一个多项式与\(3x^2 - 2x + 5\)的和是\(x^2 + x - 1\),求这个多项式。
解:设这个多项式为\(A\),根据题意可得:\(A+(3x^2 - 2x + 5)=x^2 + x - 1\)
所以\(A=(x^2 + x - 1)-(3x^2 - 2x + 5)\)\(
\begin{align*}
&=x^2 + x - 1 - 3x^2 + 2x - 5\\
&=(x^2 - 3x^2)+(x + 2x)+(-1 - 5)\\
&=-2x^2 + 3x - 6
\end{align*}
\)
答:这个多项式是\(-2x^2 + 3x - 6\)。
例 4:如图,在一个长方形空地中,有一块正方形草坪和一块长方形花坛,正方形草坪的边长为\(a\)米,长方形花坛的长为\(b\)米,宽为\(c\)米,长方形空地的长为\((3a + b)\)米,宽为\((2a + c)\)米。求空地中除了草坪和花坛之外的面积。
解:首先计算长方形空地的面积:\((3a + b)(2a + c)\)(此处暂不展开计算,仅进行整式加减相关的面积差计算)
正方形草坪的面积为\(a^2\)平方米,长方形花坛的面积为\(bc\)平方米。
则空地中除了草坪和花坛之外的面积 = 长方形空地的面积 - 正方形草坪的面积 - 长方形花坛的面积,即:
\((3a + b)(2a + c)-a^2 - bc\)(展开并化简)\(
\begin{align*}
&=6a^2 + 3ac + 2ab + bc - a^2 - bc\\
&=(6a^2 - a^2)+2ab + 3ac+(bc - bc)\\
&=5a^2 + 2ab + 3ac
\end{align*}
\)
答:空地中除了草坪和花坛之外的面积是\((5a^2 + 2ab + 3ac)\)平方米。
小练习
计算:
(1)\((2x - 3y)+(5x + 4y)\);
(2)\((8a - 7b)-(4a - 5b)\);
(3)\(3(x^2 - 2x + 1)-2(2x^2 - 3x - 3)\)。
先化简,再求值:
(1)\(3x^2 - [7x - (4x - 3)-2x^2]\),其中\(x = -1\);
(2)\(5(3a^2b - ab^2)-(ab^2 + 3a^2b)\),其中\(a = \frac{1}{2}\),\(b = -1\)。
已知一个多项式减去\(x^2 - 2y^2\)等于\(3x^2 + y^2\),求这个多项式。
一个三角形的第一条边长为\((2a + b)\)厘米,第二条边比第一条边短\((a - b)\)厘米,第三条边是第一条边与第二条边的和的一半。求这个三角形的周长。
填空:
(1)若\(A = x^2 - 2x + 1\),\(B = 3x - 2\),则\(A + B = \)。
(2)计算\((a^2 + 2ab + b^2)-(a^2 - 2ab + b^2)= \)。
(3)若多项式\(2x^2 + ax - y + 6\)与多项式\(2bx^2 - 3x + 5y - 1\)的差不含\(x^2\)项和\(x\)项,则\(a = \),\(b = \)。
思考讨论
整式加减运算的关键是什么?
整式加减运算的关键是正确地去括号和熟练地合并同类项。去括号时,要严格按照去括号法则进行,注意括号前面的符号对括号内各项符号的影响;合并同类项时,要准确找到同类项,再按照合并同类项的法则将系数相加,字母和字母的指数不变。
在进行整式加减时,如何处理多层括号?
在进行整式加减时,如果遇到多层括号,可以由内向外逐层去括号,也可以由外向内逐层去括号。每去掉一层括号后,要及时合并同类项,这样可以简化运算。例如,计算\(a - [b - (c - d)]\),可以先去小括号得\(a - [b - c + d]\),再去中括号得\(a - b + c - d\)。
课堂小结
整式加减的实质:去括号和合并同类项。
整式加减的步骤:
去括号:根据去括号法则去掉整式中的括号;
合并同类项:将去括号后的多项式中的同类项合并成一项。
整式加减的应用:可以求几个整式的和或差,也可以解决与面积、周长等相关的实际问题。
在进行整式加减时,要注意符号的变化和同类项的准确识别,以保证运算的正确性。
课后作业
教材 P78 练习 1、2、3、4 题。
计算:
(1)\((5m + 4n)-(7m - 2n)\);
(2)\(2(x^2 - xy)-3(2x^2 - 3xy)\);
(3)\(3a^2 - [5a - (\frac{1}{2}a - 3)+2a^2]\)。
先化简,再求值:
(1)\((2x^2 - y^2)-2(3y^2 - 2x^2)\),其中\(x = -1\),\(y = 2\);
(2)已知\(x + y = 3\),\(xy = -2\),求\(3(x + y)-2(xy + x + y)\)的值。
已知多项式\(A = 3x^2 - 2x + 1\),\(B = 2x^2 + 3x - 4\),求\(2A - 3B\)。
一个长方形的长为\((2x + 3)\)厘米,宽为\((x - 1)\)厘米,另一个正方形的边长为\((x + 2)\)厘米。求长方形的面积与正方形的面积的差。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掌握整式加减的运算法则,并能熟练地进行整式的加减计算.
2.能将多项式按照某一个字母的升幂(降幂)排列.
3.经历整式加减的法则概括过程,提高思考及语言表达能力,培养符号感.
学习目标
复习回顾
回顾添括号法则,在下列各题的括号内,填写适当的项:
(1)-9a2+16b2= -( );
(2)b2-4a2+4a-1=b2-( );
(3)2x-x2+y2=2x+( );
(4)2a-b-x+3y=2a-b-( );
(5)am-bn-an-bm=am+( )-bm.
9a2-16b2
4a2-4a+1
-x2+y
x-3y
-bn-an
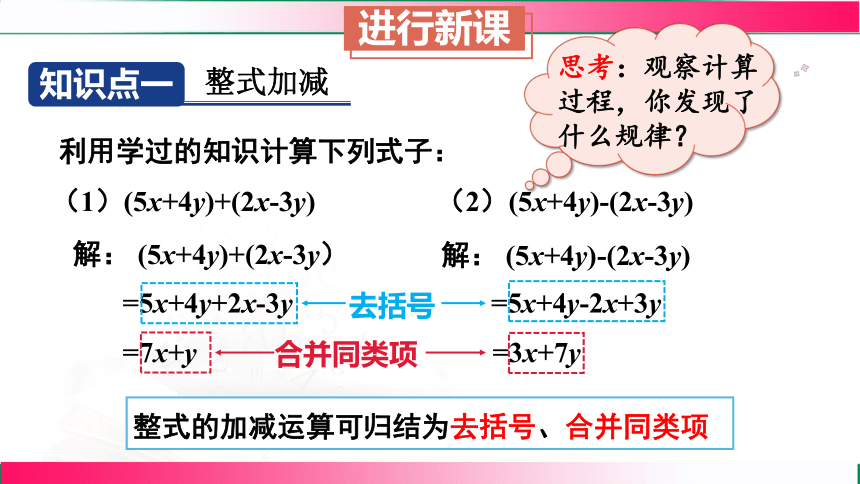
进行新课
知识点一
整式加减
利用学过的知识计算下列式子:
(1)(5x+4y)+(2x-3y)
(2)(5x+4y)-(2x-3y)
解: (5x+4y)+(2x-3y)
=5x+4y+2x-3y
=7x+y
解: (5x+4y)-(2x-3y)
=5x+4y-2x+3y
=3x+7y
整式的加减运算可归结为去括号、合并同类项
去括号
合并同类项
思考:观察计算过程,你发现了什么规律?
求多项式4-5x2+3x与-2x+7x2-3的差.
例
3
解:(4-5x2+3x)-(-2x+7x2-3)
=4-5x2+3x+2x-7x2+3
=(-5x2-7x2)+(3x+2x)+(4+3)
= -12x2+5x+7
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
整式加减的运算结果,通常将多项式按照某个字母(如x)的指数从大到小(或从小到大)依次排列,这种排列叫作关于这个字母(如x)的降(升)幂排列.
按照x的降幂排序
注意:
整式加减的结果要最简:
不能有同类项;
含字母的项的系数不能出现带分数,如果有带分数,必须将其化成假分数;
一般不含括号.
练一练:已知A=3x2-2xy+y2,B=2x2+3xy-4y2,求下列结果并按x的降幂排列:
(1)A-2B;(2)2A+B.
解:(1) A-2B
=(3x2-2xy+y2)- 2(2x2+3xy-4y2 )
=3x2-2xy+y2-4x2-6xy+8y2
= -x2-8xy+9y2
去括号时要注意括号前面系数
按照y的降幂排序
9y2-8xy-x2
练一练:已知A=3x2-2xy+y2,B=2x2+3xy-4y2,求下列结果并按x的降幂排列:
(1)A-2B;(2)2A+B.
解:(2) 2A+B
=2(3x2-2xy+y2)+( 2x2+3xy-4y2 )
=6x2-4xy+2y2+2x2+3xy-4y2
=8x2-xy-2y2
归纳:
1.几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行计算.
2.整式加减实际上就是:去括号、合并同类项.
3.整式加减的结果要最简,不能含有同类项.
4.运算结果,常将多项式按某个字母的降(升)幂排列.
知识点二
整式的化简求值
先化简,再求值.
例
4
5a2-[a2-(2a-5a2)-2(a2-3a)],其中a=4.
解:原式= 5a2-(a2-2a+5a2-2a2+6a)
= 5a2-(4a2+4a)
= 5a2-4a2-4a
= a2-4a
当a=4时,原式=a2-4a=42-4×4=0.
思考:还可以怎样化简?
由内向外,
先去小括号
由外向内,
先去大括号
解:原式= 5a2-a2+(2a-5a2)+2(a2-3a)
= 5a2-a2+ 2a-5a2+2a2-6a
= a2-4a
5a2-[a2-(2a-5a2)-2(a2-3a)],其中a=4.
当a=4时,原式=a2-4a=42-4×4=0.
先化简,再求值.
例
4
练一练:先化简,再求值:
(1)(2x2-5x+4)-3(x2-x+1),其中x= -2;
(2)3a2b+(-2ab2+a2b)-2(a2b+2ab2),其中a= -2,b= -1.
解:(1)原式= 2x2-5x+4-3x2+3x-3
= -x2-2x+1
当x= -2时,
原式= -x2-2x+1= -(-2)2-2×(-2)+1= -4+4+1=1
练一练:先化简,再求值:
(1)(2x2-5x+4)-3(x2-x+1),其中x= -2;
(2)3a2b+(-2ab2+a2b)-2(a2b+2ab2),其中a= -2,b= -1.
(2)原式=3a2b-2ab2+a2b-2a2b-4ab2
=2a2b-6ab2
当a= -2,b= -1时,
原式=2a2b-6ab2= 2×(-2)2×(-1)-6×(-2)×(-1)2
= -8+12=4
整式化简求值的一般步骤:
化:利用整式加减的运算法则将整式化简.
代:把已知字母的值代入化简后的式子.
算:依据有理数的运算法则进行计算.
1
2
3
对于某些特殊式子,可采用“整体代入”进行计算.
核心必知
1.将多项式按某个字母(如 )的指数__________(或__________)
依次排列,这种排列叫作关于这个字母(如 )的降(升)幂排列.
2.一般地,几个整式相加减,如果有括号就先去括号,然后
再合并同类项.整式加减的最后结果中不能含有同类项,即要
合并到不能再合并为止.
从大到小
从小到大
1星题 基础练
知识点1 多项式的降(升)幂排列
1.关于多项式 的说法正确的是( )
D
A.按的降幂排列 B.按 的升幂排列
C.按的降幂排列 D.按 的升幂排列
2.创新题·新题型 多项式是按字母 降
幂排列的,则 代表的项不可能是( )
B
A. B. C. D.
3.把多项式按 的降幂排列是
___________________________,按 的升幂排列的第三项是
_______.
4.(8分)把多项式 按下列要
求重新排列:
(1)按 的升幂排列;
解:按的升幂排列为 .
(2)按 的降幂排列.
按的降幂排列为 .
知识点2 整式加减
5.化简: ________.
6.[2025年1月厦门期末]已知, ,则
的结果为( )
D
A. B. C. D.
7.[2024·亳州期中]一个多项式与的和是 ,
则这个多项式为( )
C
A. B.
C. D.
【变式题】 若,则
___________________.
8.(8分)[2024·阜阳第十八中期中]化简下列各式:
(1) ;
解:原式
.
(2) .
解:原式 .
9.(8分)先化简,再求值:
,其中, .
解:原式 ,
当,时,原式 .
2星题 中档练
10.[2024·北京期中]若关于, 的多项式
不含二次项,则 的值为____.
11.小程做一道题“已知两个多项式、,计算 ”时,误
将看 作,求得结果是 .若
,则 ______________.
12.(12分)已知:, .
(1)化简: ;
解:由题意知 .
(2)若,,求 的值;
将, 代入,得
,所以
的值为54.
(3)若代数式的值与无关,求此时 的值.
由(1)知, ,
因为代数式的值与无关,所以 ,所以
.
3星题 提升练
13.(8分) 创新题·新问法 [2025·深圳模拟] 每一个新生命的
诞生都会给亲人带来欢乐和希望.我们可以把人出生的年份
减去组成这个年份的数字之和所得的差称为关联年份.例如,
提出“华氏定理”、被美国数学家贝特曼称为“中国的爱因斯
坦,足以成为全世界所有著名科学院的院士”的数学家华罗
庚出生于1910年,他的关联年份是
.
(1)某人出生于1981年,他的关联年份是_______;
(2)观察猜想:能整除这些关联年份的最大值为___.请你用所
学的数学知识说明理由.
9
解:理由:设出生年份为 ,
则关联年份为
,
所以能整除这些关联年份的最大值为9.
【思路点拨】在整式的化简求值中,当单个字母的值不易求
出或化简后的结果与已知式子相关联时,需要将已知式子的
值整体代入计算.
1.若,则整式 的值为___.
6
2.若,则整式 的值是_____.
3.已知, ,则整式
的值是____.
25
4.已知, ,则代数式
的值为____.
59
课堂小结
整式加减
整式加减的步骤
①列代数式
②去括号
③合并同类项
整式的化简求值
①化简
②值代入化简后的式子
③计算
谢谢观看!
2.2.3 整式加减
第2章 整式及其加减
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
2.2.3 整式加减
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
前面我们学习了同类项、合并同类项以及去括号和添括号的知识。合并同类项是把多项式中的同类项合并成一项;去括号和添括号是代数式变形的重要方法,它们都遵循一定的法则。今天我们要学习的整式加减,就是以这些知识为基础进行的运算。
学习目标
理解整式加减的意义,知道整式加减的实质是去括号和合并同类项。
能熟练进行整式的加减运算,包括整式的加法和减法。
能运用整式加减解决实际问题,提高分析和解决问题的能力。
感受整式加减在数学中的应用,体会数学的逻辑性和严谨性。
课堂导入
我们来看一个问题:一个长方形的长为\((3x + 2y)\)厘米,宽为\((x - y)\)厘米,那么这个长方形的周长是多少厘米呢?
长方形的周长公式是\(2 (é + )\),所以这个长方形的周长可以表示为\(2[(3x + 2y)+(x - y)]\)厘米。要算出这个结果,我们需要先去掉括号,再合并同类项,这就是整式的加减运算。通过今天的学习,我们就能轻松解决这类问题。
知识点:整式加减的意义
整式的加减就是求几个整式的和或差的运算。它的实质是运用去括号法则和合并同类项法则,将整式化简为一个最简整式(即不含同类项的整式)。
例如:
求整式\(3x + 2y\)与\(x - y\)的和,就是进行整式的加法运算,可表示为\((3x + 2y)+(x - y)\)。
求整式\(5a^2 - 3b^2\)与\(2a^2 + b^2\)的差,就是进行整式的减法运算,可表示为\((5a^2 - 3b^2)-(2a^2 + b^2)\)。
知识点:整式加减的步骤
整式加减的一般步骤如下:
去括号:如果整式加减运算中有括号,要先根据去括号法则去掉括号。如果括号前面是 “+” 号,去掉括号后,括号内的各项符号不变;如果括号前面是 “-” 号,去掉括号后,括号内的各项符号都要改变。
合并同类项:去掉括号后,按照合并同类项的法则,把多项式中的同类项合并成一项,使结果化为最简整式。
例如,计算\((3x + 2y)+(x - y)\):
去括号:\(3x + 2y + x - y\);
合并同类项:\((3x + x)+(2y - y)=4x + y\)。
再如,计算\((5a^2 - 3b^2)-(2a^2 + b^2)\):
去括号:\(5a^2 - 3b^2 - 2a^2 - b^2\);
合并同类项:\((5a^2 - 2a^2)+(-3b^2 - b^2)=3a^2 - 4b^2\)。
例题解析
例 1:计算:
(1)\((2x^2 + 3x - 1)+(x^2 - 2x + 5)\);
(2)\((4a^2b - 3ab^2)-(2a^2b - 5ab^2)\);
(3)\(3(x^2 - 2xy + y^2)-2(x^2 - xy + y^2)\)。
解:(1)\(
\begin{align*}
&(2x^2 + 3x - 1)+(x^2 - 2x + 5)\\
=&2x^2 + 3x - 1 + x^2 - 2x + 5\\
=&(2x^2 + x^2)+(3x - 2x)+(-1 + 5)\\
=&3x^2 + x + 4
\end{align*}
\)
(2)\(
\begin{align*}
&(4a^2b - 3ab^2)-(2a^2b - 5ab^2)\\
=&4a^2b - 3ab^2 - 2a^2b + 5ab^2\\
=&(4a^2b - 2a^2b)+(-3ab^2 + 5ab^2)\\
=&2a^2b + 2ab^2
\end{align*}
\)
(3)\(
\begin{align*}
&3(x^2 - 2xy + y^2)-2(x^2 - xy + y^2)\\
=&3x^2 - 6xy + 3y^2 - 2x^2 + 2xy - 2y^2\\
=&(3x^2 - 2x^2)+(-6xy + 2xy)+(3y^2 - 2y^2)\\
=&x^2 - 4xy + y^2
\end{align*}
\)
例 2:先化简,再求值:
(1)\((5x^2 - 3y^2)-(5x^2 + 3y^2)\),其中\(x = 1\),\(y = -1\);
(2)\(2(2a + b)^2 - 3(2a + b)+8(2a + b)^2 - 6(2a + b)\),其中\(a = -\frac{3}{4}\),\(b = \frac{1}{2}\)。
解:(1)先化简:\(
\begin{align*}
&(5x^2 - 3y^2)-(5x^2 + 3y^2)\\
=&5x^2 - 3y^2 - 5x^2 - 3y^2\\
=&-6y^2
\end{align*}
\)
当\(x = 1\),\(y = -1\)时,代入得:\(-6 (-1)^2=-6 1 = -6\)
(2)先化简,把\((2a + b)\)看作一个整体合并同类项:\(
\begin{align*}
&2(2a + b)^2 - 3(2a + b)+8(2a + b)^2 - 6(2a + b)\\
=&(2 + 8)(2a + b)^2+(-3 - 6)(2a + b)\\
=&10(2a + b)^2 - 9(2a + b)
\end{align*}
\)
当\(a = -\frac{3}{4}\),\(b = \frac{1}{2}\)时,计算\(2a + b\):\(2 (-\frac{3}{4})+\frac{1}{2}=-\frac{3}{2}+\frac{1}{2}=-1\)
把\(2a + b=-1\)代入化简后的式子得:\(
\begin{align*}
&10 (-1)^2 - 9 (-1)\\
=&10 1 + 9\\
=&19
\end{align*}
\)
例 3:已知一个多项式与\(3x^2 - 2x + 5\)的和是\(x^2 + x - 1\),求这个多项式。
解:设这个多项式为\(A\),根据题意可得:\(A+(3x^2 - 2x + 5)=x^2 + x - 1\)
所以\(A=(x^2 + x - 1)-(3x^2 - 2x + 5)\)\(
\begin{align*}
&=x^2 + x - 1 - 3x^2 + 2x - 5\\
&=(x^2 - 3x^2)+(x + 2x)+(-1 - 5)\\
&=-2x^2 + 3x - 6
\end{align*}
\)
答:这个多项式是\(-2x^2 + 3x - 6\)。
例 4:如图,在一个长方形空地中,有一块正方形草坪和一块长方形花坛,正方形草坪的边长为\(a\)米,长方形花坛的长为\(b\)米,宽为\(c\)米,长方形空地的长为\((3a + b)\)米,宽为\((2a + c)\)米。求空地中除了草坪和花坛之外的面积。
解:首先计算长方形空地的面积:\((3a + b)(2a + c)\)(此处暂不展开计算,仅进行整式加减相关的面积差计算)
正方形草坪的面积为\(a^2\)平方米,长方形花坛的面积为\(bc\)平方米。
则空地中除了草坪和花坛之外的面积 = 长方形空地的面积 - 正方形草坪的面积 - 长方形花坛的面积,即:
\((3a + b)(2a + c)-a^2 - bc\)(展开并化简)\(
\begin{align*}
&=6a^2 + 3ac + 2ab + bc - a^2 - bc\\
&=(6a^2 - a^2)+2ab + 3ac+(bc - bc)\\
&=5a^2 + 2ab + 3ac
\end{align*}
\)
答:空地中除了草坪和花坛之外的面积是\((5a^2 + 2ab + 3ac)\)平方米。
小练习
计算:
(1)\((2x - 3y)+(5x + 4y)\);
(2)\((8a - 7b)-(4a - 5b)\);
(3)\(3(x^2 - 2x + 1)-2(2x^2 - 3x - 3)\)。
先化简,再求值:
(1)\(3x^2 - [7x - (4x - 3)-2x^2]\),其中\(x = -1\);
(2)\(5(3a^2b - ab^2)-(ab^2 + 3a^2b)\),其中\(a = \frac{1}{2}\),\(b = -1\)。
已知一个多项式减去\(x^2 - 2y^2\)等于\(3x^2 + y^2\),求这个多项式。
一个三角形的第一条边长为\((2a + b)\)厘米,第二条边比第一条边短\((a - b)\)厘米,第三条边是第一条边与第二条边的和的一半。求这个三角形的周长。
填空:
(1)若\(A = x^2 - 2x + 1\),\(B = 3x - 2\),则\(A + B = \)。
(2)计算\((a^2 + 2ab + b^2)-(a^2 - 2ab + b^2)= \)。
(3)若多项式\(2x^2 + ax - y + 6\)与多项式\(2bx^2 - 3x + 5y - 1\)的差不含\(x^2\)项和\(x\)项,则\(a = \),\(b = \)。
思考讨论
整式加减运算的关键是什么?
整式加减运算的关键是正确地去括号和熟练地合并同类项。去括号时,要严格按照去括号法则进行,注意括号前面的符号对括号内各项符号的影响;合并同类项时,要准确找到同类项,再按照合并同类项的法则将系数相加,字母和字母的指数不变。
在进行整式加减时,如何处理多层括号?
在进行整式加减时,如果遇到多层括号,可以由内向外逐层去括号,也可以由外向内逐层去括号。每去掉一层括号后,要及时合并同类项,这样可以简化运算。例如,计算\(a - [b - (c - d)]\),可以先去小括号得\(a - [b - c + d]\),再去中括号得\(a - b + c - d\)。
课堂小结
整式加减的实质:去括号和合并同类项。
整式加减的步骤:
去括号:根据去括号法则去掉整式中的括号;
合并同类项:将去括号后的多项式中的同类项合并成一项。
整式加减的应用:可以求几个整式的和或差,也可以解决与面积、周长等相关的实际问题。
在进行整式加减时,要注意符号的变化和同类项的准确识别,以保证运算的正确性。
课后作业
教材 P78 练习 1、2、3、4 题。
计算:
(1)\((5m + 4n)-(7m - 2n)\);
(2)\(2(x^2 - xy)-3(2x^2 - 3xy)\);
(3)\(3a^2 - [5a - (\frac{1}{2}a - 3)+2a^2]\)。
先化简,再求值:
(1)\((2x^2 - y^2)-2(3y^2 - 2x^2)\),其中\(x = -1\),\(y = 2\);
(2)已知\(x + y = 3\),\(xy = -2\),求\(3(x + y)-2(xy + x + y)\)的值。
已知多项式\(A = 3x^2 - 2x + 1\),\(B = 2x^2 + 3x - 4\),求\(2A - 3B\)。
一个长方形的长为\((2x + 3)\)厘米,宽为\((x - 1)\)厘米,另一个正方形的边长为\((x + 2)\)厘米。求长方形的面积与正方形的面积的差。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掌握整式加减的运算法则,并能熟练地进行整式的加减计算.
2.能将多项式按照某一个字母的升幂(降幂)排列.
3.经历整式加减的法则概括过程,提高思考及语言表达能力,培养符号感.
学习目标
复习回顾
回顾添括号法则,在下列各题的括号内,填写适当的项:
(1)-9a2+16b2= -( );
(2)b2-4a2+4a-1=b2-( );
(3)2x-x2+y2=2x+( );
(4)2a-b-x+3y=2a-b-( );
(5)am-bn-an-bm=am+( )-bm.
9a2-16b2
4a2-4a+1
-x2+y
x-3y
-bn-an
进行新课
知识点一
整式加减
利用学过的知识计算下列式子:
(1)(5x+4y)+(2x-3y)
(2)(5x+4y)-(2x-3y)
解: (5x+4y)+(2x-3y)
=5x+4y+2x-3y
=7x+y
解: (5x+4y)-(2x-3y)
=5x+4y-2x+3y
=3x+7y
整式的加减运算可归结为去括号、合并同类项
去括号
合并同类项
思考:观察计算过程,你发现了什么规律?
求多项式4-5x2+3x与-2x+7x2-3的差.
例
3
解:(4-5x2+3x)-(-2x+7x2-3)
=4-5x2+3x+2x-7x2+3
=(-5x2-7x2)+(3x+2x)+(4+3)
= -12x2+5x+7
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
整式加减的运算结果,通常将多项式按照某个字母(如x)的指数从大到小(或从小到大)依次排列,这种排列叫作关于这个字母(如x)的降(升)幂排列.
按照x的降幂排序
注意:
整式加减的结果要最简:
不能有同类项;
含字母的项的系数不能出现带分数,如果有带分数,必须将其化成假分数;
一般不含括号.
练一练:已知A=3x2-2xy+y2,B=2x2+3xy-4y2,求下列结果并按x的降幂排列:
(1)A-2B;(2)2A+B.
解:(1) A-2B
=(3x2-2xy+y2)- 2(2x2+3xy-4y2 )
=3x2-2xy+y2-4x2-6xy+8y2
= -x2-8xy+9y2
去括号时要注意括号前面系数
按照y的降幂排序
9y2-8xy-x2
练一练:已知A=3x2-2xy+y2,B=2x2+3xy-4y2,求下列结果并按x的降幂排列:
(1)A-2B;(2)2A+B.
解:(2) 2A+B
=2(3x2-2xy+y2)+( 2x2+3xy-4y2 )
=6x2-4xy+2y2+2x2+3xy-4y2
=8x2-xy-2y2
归纳:
1.几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行计算.
2.整式加减实际上就是:去括号、合并同类项.
3.整式加减的结果要最简,不能含有同类项.
4.运算结果,常将多项式按某个字母的降(升)幂排列.
知识点二
整式的化简求值
先化简,再求值.
例
4
5a2-[a2-(2a-5a2)-2(a2-3a)],其中a=4.
解:原式= 5a2-(a2-2a+5a2-2a2+6a)
= 5a2-(4a2+4a)
= 5a2-4a2-4a
= a2-4a
当a=4时,原式=a2-4a=42-4×4=0.
思考:还可以怎样化简?
由内向外,
先去小括号
由外向内,
先去大括号
解:原式= 5a2-a2+(2a-5a2)+2(a2-3a)
= 5a2-a2+ 2a-5a2+2a2-6a
= a2-4a
5a2-[a2-(2a-5a2)-2(a2-3a)],其中a=4.
当a=4时,原式=a2-4a=42-4×4=0.
先化简,再求值.
例
4
练一练:先化简,再求值:
(1)(2x2-5x+4)-3(x2-x+1),其中x= -2;
(2)3a2b+(-2ab2+a2b)-2(a2b+2ab2),其中a= -2,b= -1.
解:(1)原式= 2x2-5x+4-3x2+3x-3
= -x2-2x+1
当x= -2时,
原式= -x2-2x+1= -(-2)2-2×(-2)+1= -4+4+1=1
练一练:先化简,再求值:
(1)(2x2-5x+4)-3(x2-x+1),其中x= -2;
(2)3a2b+(-2ab2+a2b)-2(a2b+2ab2),其中a= -2,b= -1.
(2)原式=3a2b-2ab2+a2b-2a2b-4ab2
=2a2b-6ab2
当a= -2,b= -1时,
原式=2a2b-6ab2= 2×(-2)2×(-1)-6×(-2)×(-1)2
= -8+12=4
整式化简求值的一般步骤:
化:利用整式加减的运算法则将整式化简.
代:把已知字母的值代入化简后的式子.
算:依据有理数的运算法则进行计算.
1
2
3
对于某些特殊式子,可采用“整体代入”进行计算.
核心必知
1.将多项式按某个字母(如 )的指数__________(或__________)
依次排列,这种排列叫作关于这个字母(如 )的降(升)幂排列.
2.一般地,几个整式相加减,如果有括号就先去括号,然后
再合并同类项.整式加减的最后结果中不能含有同类项,即要
合并到不能再合并为止.
从大到小
从小到大
1星题 基础练
知识点1 多项式的降(升)幂排列
1.关于多项式 的说法正确的是( )
D
A.按的降幂排列 B.按 的升幂排列
C.按的降幂排列 D.按 的升幂排列
2.创新题·新题型 多项式是按字母 降
幂排列的,则 代表的项不可能是( )
B
A. B. C. D.
3.把多项式按 的降幂排列是
___________________________,按 的升幂排列的第三项是
_______.
4.(8分)把多项式 按下列要
求重新排列:
(1)按 的升幂排列;
解:按的升幂排列为 .
(2)按 的降幂排列.
按的降幂排列为 .
知识点2 整式加减
5.化简: ________.
6.[2025年1月厦门期末]已知, ,则
的结果为( )
D
A. B. C. D.
7.[2024·亳州期中]一个多项式与的和是 ,
则这个多项式为( )
C
A. B.
C. D.
【变式题】 若,则
___________________.
8.(8分)[2024·阜阳第十八中期中]化简下列各式:
(1) ;
解:原式
.
(2) .
解:原式 .
9.(8分)先化简,再求值:
,其中, .
解:原式 ,
当,时,原式 .
2星题 中档练
10.[2024·北京期中]若关于, 的多项式
不含二次项,则 的值为____.
11.小程做一道题“已知两个多项式、,计算 ”时,误
将看 作,求得结果是 .若
,则 ______________.
12.(12分)已知:, .
(1)化简: ;
解:由题意知 .
(2)若,,求 的值;
将, 代入,得
,所以
的值为54.
(3)若代数式的值与无关,求此时 的值.
由(1)知, ,
因为代数式的值与无关,所以 ,所以
.
3星题 提升练
13.(8分) 创新题·新问法 [2025·深圳模拟] 每一个新生命的
诞生都会给亲人带来欢乐和希望.我们可以把人出生的年份
减去组成这个年份的数字之和所得的差称为关联年份.例如,
提出“华氏定理”、被美国数学家贝特曼称为“中国的爱因斯
坦,足以成为全世界所有著名科学院的院士”的数学家华罗
庚出生于1910年,他的关联年份是
.
(1)某人出生于1981年,他的关联年份是_______;
(2)观察猜想:能整除这些关联年份的最大值为___.请你用所
学的数学知识说明理由.
9
解:理由:设出生年份为 ,
则关联年份为
,
所以能整除这些关联年份的最大值为9.
【思路点拨】在整式的化简求值中,当单个字母的值不易求
出或化简后的结果与已知式子相关联时,需要将已知式子的
值整体代入计算.
1.若,则整式 的值为___.
6
2.若,则整式 的值是_____.
3.已知, ,则整式
的值是____.
25
4.已知, ,则代数式
的值为____.
59
课堂小结
整式加减
整式加减的步骤
①列代数式
②去括号
③合并同类项
整式的化简求值
①化简
②值代入化简后的式子
③计算
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
