3.2.1利用移项、去括号解一元一次方程 课件(共41张PPT)
文档属性
| 名称 | 3.2.1利用移项、去括号解一元一次方程 课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览











文档简介
(共41张PPT)
3.2.1利用移项、去括号解一元一次方程
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
利用移项、去括号解一元一次方程
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
上节课我们学习了等式的基本性质,知道等式两边同时加上(或减去)同一个整式,或者同时乘(或除以)同一个不为 0 的数,等式仍然成立。这为我们解方程提供了重要依据。今天我们将学习利用移项和去括号来解一元一次方程。
学习目标
理解移项的概念,掌握移项的法则和依据。
能熟练运用去括号法则和移项法则解含有括号的一元一次方程。
经历解一元一次方程的过程,体会转化的数学思想。
提高运算的准确性和规范性,培养严谨的解题习惯。
课堂导入
我们来看一个方程:\(4x + 5 = 2x + 11\)。如何求出这个方程的解呢?根据等式的基本性质 1,我们可以在等式两边同时减去\(2x\),得到\(4x - 2x + 5 = 11\);再在等式两边同时减去 5,得到\(4x - 2x = 11 - 5\)。像这样,把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。移项是解方程的重要步骤,它可以使方程变得更简单。
再看一个含有括号的方程:\(2(x - 3) + 5 = 13\)。要解这个方程,我们需要先去掉括号,再进行移项等操作。那么,如何正确地去括号和移项呢?这就是我们本节课要重点学习的内容。
知识点:移项
定义
把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。
依据
移项的依据是等式的基本性质 1。例如,对于方程\(x + 3 = 5\),根据等式的基本性质 1,两边同时减去 3,得到\(x = 5 - 3\),这里的 “\(+3\)” 从左边移到右边后变成了 “\(-3\)”,就是移项。
注意事项
移项时,被移的项一定要改变符号,不移动的项符号不变。例如,方程\(3x - 2 = 2x + 1\),移项后得到\(3x - 2x = 1 + 2\),而不是\(3x + 2x = 1 - 2\)。
移项的目的是把含有未知数的项移到方程的一边,把常数项移到方程的另一边,使方程更接近\(ax = b\)(\(a 0\))的形式。
知识点:去括号法则在解方程中的应用
在解含有括号的一元一次方程时,需要先按照去括号法则去掉括号,再进行移项等操作。去括号法则如下:
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同。例如,\(2(x + 3)=2x + 6\)。
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。例如,\(-3(x - 2)=-3x + 6\)。
注意事项
去括号时,要将括号外的因数与括号内的每一项都相乘,不能漏乘。例如,\(3(2x - 1)=6x - 3\),不能写成\(6x - 1\)。
当括号前面是 “\(-\)” 号时,去掉括号后,括号内的各项都要改变符号,千万不要忘记改变括号内每一项的符号。
解含有括号的一元一次方程的步骤
去括号:按照去括号法则去掉方程中的括号。
移项:把含有未知数的项移到方程的一边,常数项移到方程的另一边(移项要变号)。
合并同类项:把方程化成\(ax = b\)(\(a 0\))的形式。
系数化为 1:根据等式的基本性质 2,方程两边同时除以未知数的系数\(a\),得到方程的解\(x=\frac{b}{a}\)。
例题解析
例 1:解下列方程:
(1)\(4x + 5 = 2x + 11\);
(2)\(7x - 3 = 5x + 9\)。
解:(1)移项,得:\(4x - 2x = 11 - 5\)
合并同类项,得:\(2x = 6\)
系数化为 1,得:\(x = 3\)
(2)移项,得:\(7x - 5x = 9 + 3\)
合并同类项,得:\(2x = 12\)
系数化为 1,得:\(x = 6\)
例 2:解下列方程:
(1)\(2(x - 3) + 5 = 13\);
(2)\(3(2x + 1) - 2(x - 2) = 25\)。
解:(1)去括号,得:\(2x - 6 + 5 = 13\)
合并同类项,得:\(2x - 1 = 13\)
移项,得:\(2x = 13 + 1\)\(2x = 14\)
系数化为 1,得:\(x = 7\)
(2)去括号,得:\(6x + 3 - 2x + 4 = 25\)
合并同类项,得:\(4x + 7 = 25\)
移项,得:\(4x = 25 - 7\)\(4x = 18\)
系数化为 1,得:\(x=\frac{9}{2}\)
例 3:解下列方程:
(1)\(5 - 3(x - 1)=1\);
(2)\(\frac{1}{2}(4x - 6)-\frac{1}{3}(6x + 3)=1\)。
解:(1)去括号,得:\(5 - 3x + 3 = 1\)
合并同类项,得:\(-3x + 8 = 1\)
移项,得:\(-3x = 1 - 8\)\(-3x = -7\)
系数化为 1,得:\(x=\frac{7}{3}\)
(2)去括号,得:\(2x - 3 - 2x - 1 = 1\)
合并同类项,得:\(-4 = 1\)
显然,这个等式不成立,所以原方程无解。
例 4:当\(x\)为何值时,代数式\(2(x - 1) + 3\)的值等于代数式\(3x + 1\)的值?
解:根据题意,可列出方程:\(2(x - 1) + 3 = 3x + 1\)
去括号,得:\(2x - 2 + 3 = 3x + 1\)
合并同类项,得:\(2x + 1 = 3x + 1\)
移项,得:\(2x - 3x = 1 - 1\)\(-x = 0\)
系数化为 1,得:\(x = 0\)
答:当\(x = 0\)时,两个代数式的值相等。
小练习
解下列方程:
(1)\(3x + 7 = 5x - 1\);
(2)\(6x - 5 = 3x + 4\);
(3)\(4(x + 2) - 3 = 17\);
(4)\(2(3x - 1) - 3(x + 2) = 1\);
(5)\(5 - 2(x - 3)=1\);
(6)\(\frac{1}{3}(3x - 6)-\frac{1}{2}(2x + 4)=0\)。
当\(x\)为何值时,代数式\(3x - 2\)的值比代数式\(2x + 3\)的值大 5?
已知关于\(x\)的方程\(2(x + 1) - m = -2(m - 2)\)的解是\(x = -2\),求\(m\)的值。
填空:
(1)方程\(3x + 5 = 2x - 4\)移项后得( )。
(2)方程\(2(x - 1) = 3x + 4\)去括号后得( )。
(3)若方程\(ax + b = 0\)(\(a 0\))的解是\(x = 5\),则方程\(a(x + 3) + b = 0\)(\(a 0\))的解是( )。
思考讨论
移项和交换律有什么区别?
移项是把方程中的某一项从一边移到另一边时改变符号,它的依据是等式的基本性质 1;而交换律是在同一个数的运算中,交换加数或因数的位置,符号不变。例如,在\(a + b = b + a\)中,运用的是加法交换律,符号没有改变;而在方程\(x + 3 = 5\)移项得到\(x = 5 - 3\)中,“\(+3\)” 变成了 “\(-3\)”,是移项。
解含有括号的一元一次方程时,去括号要注意什么?
解含有括号的一元一次方程时,去括号要注意以下几点:一是要将括号外的因数与括号内的每一项都相乘,不能漏乘;二是当括号前面是 “\(-\)” 号时,去掉括号后,括号内的各项都要改变符号;三是如果括号前面有系数,要先把系数乘进去,再去括号,或者先去括号,再处理系数,具体方法可以根据方程的特点选择。
课堂小结
移项:把方程中的某一项改变符号后,从方程的一边移到另一边,依据是等式的基本性质 1,移项时要注意变号。
去括号:解含有括号的方程时,要先按照去括号法则去掉括号,注意不要漏乘和符号的变化。
解含有括号的一元一次方程的步骤:去括号→移项→合并同类项→系数化为 1。
在解方程的过程中,要认真仔细,每一步都要依据相应的法则或性质,确保运算的准确性。
课后作业
解下列方程:
(1)\(5x - 2 = 7x + 8\);
(2)\(3(x - 2) + 1 = x - (2x - 1)\);
(3)\(4 - 3(2 - x)=5x\);
(4)\(\frac{1}{2}(x + 1)-\frac{1}{3}(x - 1)=1\)。
当\(x\)为何值时,代数式\(2(3x - 1)\)的值与代数式\(5 - (x + 1)\)的值相等?
已知关于\(x\)的方程\(3x - 2m = 4\)的解是\(x = m\),求\(m\)的值。
若方程\(2x + 3 = 5\)与方程\(2 - \frac{a - x}{3}=0\)的解相同,求\(a\)的值。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
复习回顾
判断下列各式哪些是方程
7-1=6
3x-3=21
x-1
x>3
36+x=2(12+x)
a2-1=0
b2≠-1
4y+2=5y-5
√
√
√
√
√
含有未知数的等式叫作方程.
方程的两边都是整式,这样的方程称为整式方程.
探索新知
观察下面的方程,它们有什么共同特征
3x-3=21
36+x=2(12+x)
4y+2=5y-5
共同点:
1.只含有一个未知数(元).
2.未知数的次数都是1.
3.等号两边都是整式.
定义:只含有一个未知数(元),未知数的次数是1,且等式两边都是整式的方程叫作一元一次方程.
下列式子中,是一元一次方程的是_______(填序号).
① 1+4=2+3;② x + y=1;③ =3;④ x2-2x-1=0;
⑤ =3;⑥ 6+5y=2y-3.
练一练
③⑥
3x-3=21
仔细观察以下解答过程:
解:3x-3+3=21+3
3x=24
x=8
3x-3=21
解:3x=21+3
3x=24
x=8
你发现了什么?
你觉得这两种方法都对吗?哪种形式更好?
定义:把方程中某一项改变符号后,从方程的一边移到另一边,这种变形叫作移项.
依据是等式的性质1
移项要变号!
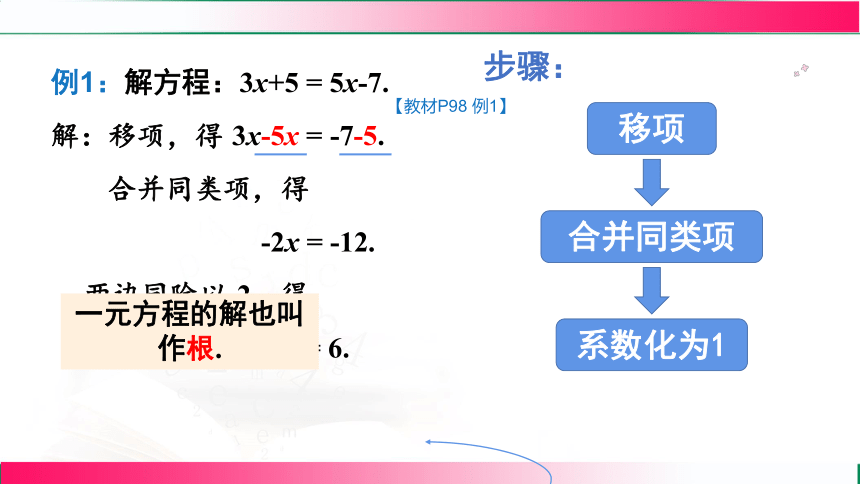
例1:解方程:3x+5 = 5x-7.
解:移项,得
3x-5x = -7-5.
合并同类项,得
-2x = -12.
两边同除以-2,得
x = 6.
移项
合并同类项
系数化为1
步骤:
一元方程的解也叫作根.
【教材P98 例1】
练一练
解下列方程:
(1)8x=4x+1; (2)2-3x = 5x+10.
解:移项,得-3x-5x = 10-2.
合并同类项,得-8x = 8.
两边同除以-8,得x = -1.
解:移项,得8x-4x = 1.
合并同类项,得 4x = 1.
两边同除以4,得 x = .
注意:①方程的各项包括它前面的符号;
②移项时,不管是把某一项从左边移到右边还是从右边移到左边,都要变号.
例2:解方程:2(x-2)-3(4x-1) = 9(1-x).
思考:这个方程要怎么解?要先做什么?
先去括号.
解:去括号,得
2x-4-12x+3 = 9-9x.
移项,得
2x-12x+9x = 9+4-3.
合并同类项,得
-x = 10.
两边同除以-1,得
x = -10.
步骤:
去括号
移项
合并同类项
系数化为1
解一元一次方程:目标向 x = a 的形式转化.
【教材P99 例2】
随堂练习
1.下面的移项对不对 如果不对,错在哪里 应当怎样改正
(1)由9+x=7,得x=7+9;
(2)由5x=7-4x,得5x-4x=7;
(3)由2y-1=3y+6,得2y-3y=6-1.
【教材P99 练习 第1题】
不对,9移项没变号,改正:x=7-9.
不对,-4x移项没变号,改正:5x+4x=7.
不对,-1移项没变号,改正:2y-3y=6+1.
2.下面解方程的过程正确吗 请说明理由.
解方程:3(y-3)-5(1+y) = 7(y-1).
解:去括号,得 3y-3-5+5y = 7y-1.
移项,得 3y+5y-7y = -1+3-5.
合并同类项,得 y = -3.
【教材P99 练习 第2题】
解:不正确. 理由:①3(y-3)与7(y-1)去括号时漏乘常数项;②-5(1+y)去括号时弄错符号;③-5移项时未变号.
3.解下列方程:
(1)5x+21=7-2x; (2)2x- =- x+2;
(3)0.5(m+8)-0.6(2m-7)=1.9;(4)3(2y+1)=2(1+y)+3(y+3).
(1)解:移项,得5x+2x = 7-21.
合并同类项,得7x = -14.
两边同除以7,得x = -2.
【教材P100 练习 第3题】
3.解下列方程:
(1)5x+21=7-2x; (2)2x- =- x+2;
(3)0.5(m+8)-0.6(2m-7)=1.9;(4)3(2y+1)=2(1+y)+3(y+3).
【教材P100 练习 第3题】
(2)解:移项,得2x+ x = 2+ .
合并同类项,得 x = .
两边同除以 ,得x = 1.
3.解下列方程:
(1)5x+21=7-2x; (2)2x- =- x+2;
(3)0.5(m+8)-0.6(2m-7)=1.9;(4)3(2y+1)=2(1+y)+3(y+3).
【教材P100 练习 第3题】
(3)解:去括号,得0.5m+4-1.2m+4.2 = 1.9.
移项,得0.5m-1.2m = 1.9-4-4.2.
合并同类项,得-0.7m = -6.3.
两边同除以-0.7,得m = 9.
3.解下列方程:
(1)5x+21=7-2x; (2)2x- =- x+2;
(3)0.5(m+8)-0.6(2m-7)=1.9;(4)3(2y+1)=2(1+y)+3(y+3).
【教材P100 练习 第3题】
(4)解:去括号,得6y+3 = 2+2y+3y+9.
移项,得6y-2y-3y = 2+9-3.
合并同类项,得y = 8.
4.解方程:7(1-2x)+11(1-2x)=2x-1.
你有几种解法?
方法1:
解:去括号得7-14x+11-22x=2x-1
移项,得-14x-22x-2x=-1-7-11
合并同类项,得-38x=-19
系数化为1得x= .
方法2:
解:7(1-2x)+11(1-2x)=-(1-2x)
移项得7(1-2x)+11(1-2x)+(1-2x)=0
合并同类项得(7+11+1)(1-2x)=0
19(1-2x)=0
1-2x=0
移项,得-2x=0-1
化系数为1,得x= .
利用整体思想,叫作换元法。
1星题 基础练
知识点1 一元一次方程的概念
1.[2025·安庆月考]下列方程中是一元一次方程的是( )
C
A. B.
C. D.
2.[2024·阜阳期中]已知 是一元一次方程,则
的值为___.
1
知识点2 移项
3.[知识初练]如图,将方程
移项,令含有未知数
的项移到等号的____边,需要注意
的是移项要______,故“ ”处应填
写的是_____.
左
变号
4.将方程 移项,正确的是( )
D
A. B.
C. D.
5.(8分)判断下列方程的变形是否正确,如果不正确请改正.
(1)由得 ;
解:不正确. 改正:由得 .
(2)由得 ;
不正确. 改正:由得 .
(3)由得 ;
正确.
(4)由得 .
不正确. 改正:由得 .
知识点3 移项解一元一次方程(不含括号)
6.[知识初练]解方程 的一般步骤:
解:移项,得___________________,
合并同类项,得____________,
两边同除以 ,得______.
7.若的值是12,则 的值是___.
5
8.(8分)教材改编题 解方程:
(1) ;
解:移项,得,合并同类项,得 ,
两边同除以2,得 .
(2) .
解:移项,得 ,合并同类项,得
,两边同除以,得 .
知识点4 移项解一元一次方程(含括号)
9.[知识初练]解方程 的一般步骤:
解:去括号,得_____________________,
移项,得_____________________,
合并同类项,得_________,
两边同除以4,得______.
10.[2025年1月芜湖期末]将方程 去括号,
得________________.
11.(8分)教材改编题 解方程:
(1) ;
解:去括号,得 ,移项、合并同类项,得
,两边同除以,得 .
(2) .
解:去括号,得 ,移项、合并同类项,
得,两边同除以,得 .
2星题 中档练
12.易错题[2025年1月合肥期末] 方程
是关于的一元一次方程,则 ( )
B
A.2 B. C. D.
13.[2025年1月淮北期末]王涵同学在解关于 的方程
时,误将“”看成了“ ”,得到方程的解为
,那么原方程的解为( )
A
A. B. C. D.
14.创新题·新考法 规定一种新运算: ,若
,则 的值为( )
A
A. B.1 C.2 D.
15.若关于的方程的解比 的解小
8,则 的值为___.
1
16.(8分)解下列方程:
(1) ;
解:去括号,得 ,
移项,得 ,
合并同类项,得,系数化为1,得 .
(2) .
解:去中括号,得 ,
去小括号,得 ,移项、合并同类项,得
,两边同除以,得 .
17.(8分)[2025·上海模拟]解方程: .
解:去括号,得 .①
移项,得 .②
合并同类项,得 .③
两边同除以2,得
上述解答过程从哪一步开始出错?指出并写出正确的解答过程.
解:解答过程从第①步开始出错.正确的解答过程如下:去括
号,得 ,
移项,得,合并同类项,得 ,
两边同除以2,得 .
3星题 提升练
18.(8分)分类讨论思想先阅读下面的解题过程,然后解答后
面的问题.
解方程: .
解:当时,原方程可化为 ,
解得 ;
当时,原方程可化为 ,
解得 .
所以原方程的解是或 .
解方程: .
解:当时,原方程可化为,解得 ;
当时,原方程可化为,解得 .
所以原方程的解是或 .
课堂小结
解一元一次方程步骤:
去括号
移项
合并同类项
系数化为1
解一元一次方程:目标向 x = a 的形式转化.
谢谢观看!
3.2.1利用移项、去括号解一元一次方程
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
利用移项、去括号解一元一次方程
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
上节课我们学习了等式的基本性质,知道等式两边同时加上(或减去)同一个整式,或者同时乘(或除以)同一个不为 0 的数,等式仍然成立。这为我们解方程提供了重要依据。今天我们将学习利用移项和去括号来解一元一次方程。
学习目标
理解移项的概念,掌握移项的法则和依据。
能熟练运用去括号法则和移项法则解含有括号的一元一次方程。
经历解一元一次方程的过程,体会转化的数学思想。
提高运算的准确性和规范性,培养严谨的解题习惯。
课堂导入
我们来看一个方程:\(4x + 5 = 2x + 11\)。如何求出这个方程的解呢?根据等式的基本性质 1,我们可以在等式两边同时减去\(2x\),得到\(4x - 2x + 5 = 11\);再在等式两边同时减去 5,得到\(4x - 2x = 11 - 5\)。像这样,把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。移项是解方程的重要步骤,它可以使方程变得更简单。
再看一个含有括号的方程:\(2(x - 3) + 5 = 13\)。要解这个方程,我们需要先去掉括号,再进行移项等操作。那么,如何正确地去括号和移项呢?这就是我们本节课要重点学习的内容。
知识点:移项
定义
把方程中的某一项改变符号后,从方程的一边移到另一边,这种变形叫做移项。
依据
移项的依据是等式的基本性质 1。例如,对于方程\(x + 3 = 5\),根据等式的基本性质 1,两边同时减去 3,得到\(x = 5 - 3\),这里的 “\(+3\)” 从左边移到右边后变成了 “\(-3\)”,就是移项。
注意事项
移项时,被移的项一定要改变符号,不移动的项符号不变。例如,方程\(3x - 2 = 2x + 1\),移项后得到\(3x - 2x = 1 + 2\),而不是\(3x + 2x = 1 - 2\)。
移项的目的是把含有未知数的项移到方程的一边,把常数项移到方程的另一边,使方程更接近\(ax = b\)(\(a 0\))的形式。
知识点:去括号法则在解方程中的应用
在解含有括号的一元一次方程时,需要先按照去括号法则去掉括号,再进行移项等操作。去括号法则如下:
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同。例如,\(2(x + 3)=2x + 6\)。
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。例如,\(-3(x - 2)=-3x + 6\)。
注意事项
去括号时,要将括号外的因数与括号内的每一项都相乘,不能漏乘。例如,\(3(2x - 1)=6x - 3\),不能写成\(6x - 1\)。
当括号前面是 “\(-\)” 号时,去掉括号后,括号内的各项都要改变符号,千万不要忘记改变括号内每一项的符号。
解含有括号的一元一次方程的步骤
去括号:按照去括号法则去掉方程中的括号。
移项:把含有未知数的项移到方程的一边,常数项移到方程的另一边(移项要变号)。
合并同类项:把方程化成\(ax = b\)(\(a 0\))的形式。
系数化为 1:根据等式的基本性质 2,方程两边同时除以未知数的系数\(a\),得到方程的解\(x=\frac{b}{a}\)。
例题解析
例 1:解下列方程:
(1)\(4x + 5 = 2x + 11\);
(2)\(7x - 3 = 5x + 9\)。
解:(1)移项,得:\(4x - 2x = 11 - 5\)
合并同类项,得:\(2x = 6\)
系数化为 1,得:\(x = 3\)
(2)移项,得:\(7x - 5x = 9 + 3\)
合并同类项,得:\(2x = 12\)
系数化为 1,得:\(x = 6\)
例 2:解下列方程:
(1)\(2(x - 3) + 5 = 13\);
(2)\(3(2x + 1) - 2(x - 2) = 25\)。
解:(1)去括号,得:\(2x - 6 + 5 = 13\)
合并同类项,得:\(2x - 1 = 13\)
移项,得:\(2x = 13 + 1\)\(2x = 14\)
系数化为 1,得:\(x = 7\)
(2)去括号,得:\(6x + 3 - 2x + 4 = 25\)
合并同类项,得:\(4x + 7 = 25\)
移项,得:\(4x = 25 - 7\)\(4x = 18\)
系数化为 1,得:\(x=\frac{9}{2}\)
例 3:解下列方程:
(1)\(5 - 3(x - 1)=1\);
(2)\(\frac{1}{2}(4x - 6)-\frac{1}{3}(6x + 3)=1\)。
解:(1)去括号,得:\(5 - 3x + 3 = 1\)
合并同类项,得:\(-3x + 8 = 1\)
移项,得:\(-3x = 1 - 8\)\(-3x = -7\)
系数化为 1,得:\(x=\frac{7}{3}\)
(2)去括号,得:\(2x - 3 - 2x - 1 = 1\)
合并同类项,得:\(-4 = 1\)
显然,这个等式不成立,所以原方程无解。
例 4:当\(x\)为何值时,代数式\(2(x - 1) + 3\)的值等于代数式\(3x + 1\)的值?
解:根据题意,可列出方程:\(2(x - 1) + 3 = 3x + 1\)
去括号,得:\(2x - 2 + 3 = 3x + 1\)
合并同类项,得:\(2x + 1 = 3x + 1\)
移项,得:\(2x - 3x = 1 - 1\)\(-x = 0\)
系数化为 1,得:\(x = 0\)
答:当\(x = 0\)时,两个代数式的值相等。
小练习
解下列方程:
(1)\(3x + 7 = 5x - 1\);
(2)\(6x - 5 = 3x + 4\);
(3)\(4(x + 2) - 3 = 17\);
(4)\(2(3x - 1) - 3(x + 2) = 1\);
(5)\(5 - 2(x - 3)=1\);
(6)\(\frac{1}{3}(3x - 6)-\frac{1}{2}(2x + 4)=0\)。
当\(x\)为何值时,代数式\(3x - 2\)的值比代数式\(2x + 3\)的值大 5?
已知关于\(x\)的方程\(2(x + 1) - m = -2(m - 2)\)的解是\(x = -2\),求\(m\)的值。
填空:
(1)方程\(3x + 5 = 2x - 4\)移项后得( )。
(2)方程\(2(x - 1) = 3x + 4\)去括号后得( )。
(3)若方程\(ax + b = 0\)(\(a 0\))的解是\(x = 5\),则方程\(a(x + 3) + b = 0\)(\(a 0\))的解是( )。
思考讨论
移项和交换律有什么区别?
移项是把方程中的某一项从一边移到另一边时改变符号,它的依据是等式的基本性质 1;而交换律是在同一个数的运算中,交换加数或因数的位置,符号不变。例如,在\(a + b = b + a\)中,运用的是加法交换律,符号没有改变;而在方程\(x + 3 = 5\)移项得到\(x = 5 - 3\)中,“\(+3\)” 变成了 “\(-3\)”,是移项。
解含有括号的一元一次方程时,去括号要注意什么?
解含有括号的一元一次方程时,去括号要注意以下几点:一是要将括号外的因数与括号内的每一项都相乘,不能漏乘;二是当括号前面是 “\(-\)” 号时,去掉括号后,括号内的各项都要改变符号;三是如果括号前面有系数,要先把系数乘进去,再去括号,或者先去括号,再处理系数,具体方法可以根据方程的特点选择。
课堂小结
移项:把方程中的某一项改变符号后,从方程的一边移到另一边,依据是等式的基本性质 1,移项时要注意变号。
去括号:解含有括号的方程时,要先按照去括号法则去掉括号,注意不要漏乘和符号的变化。
解含有括号的一元一次方程的步骤:去括号→移项→合并同类项→系数化为 1。
在解方程的过程中,要认真仔细,每一步都要依据相应的法则或性质,确保运算的准确性。
课后作业
解下列方程:
(1)\(5x - 2 = 7x + 8\);
(2)\(3(x - 2) + 1 = x - (2x - 1)\);
(3)\(4 - 3(2 - x)=5x\);
(4)\(\frac{1}{2}(x + 1)-\frac{1}{3}(x - 1)=1\)。
当\(x\)为何值时,代数式\(2(3x - 1)\)的值与代数式\(5 - (x + 1)\)的值相等?
已知关于\(x\)的方程\(3x - 2m = 4\)的解是\(x = m\),求\(m\)的值。
若方程\(2x + 3 = 5\)与方程\(2 - \frac{a - x}{3}=0\)的解相同,求\(a\)的值。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
复习回顾
判断下列各式哪些是方程
7-1=6
3x-3=21
x-1
x>3
36+x=2(12+x)
a2-1=0
b2≠-1
4y+2=5y-5
√
√
√
√
√
含有未知数的等式叫作方程.
方程的两边都是整式,这样的方程称为整式方程.
探索新知
观察下面的方程,它们有什么共同特征
3x-3=21
36+x=2(12+x)
4y+2=5y-5
共同点:
1.只含有一个未知数(元).
2.未知数的次数都是1.
3.等号两边都是整式.
定义:只含有一个未知数(元),未知数的次数是1,且等式两边都是整式的方程叫作一元一次方程.
下列式子中,是一元一次方程的是_______(填序号).
① 1+4=2+3;② x + y=1;③ =3;④ x2-2x-1=0;
⑤ =3;⑥ 6+5y=2y-3.
练一练
③⑥
3x-3=21
仔细观察以下解答过程:
解:3x-3+3=21+3
3x=24
x=8
3x-3=21
解:3x=21+3
3x=24
x=8
你发现了什么?
你觉得这两种方法都对吗?哪种形式更好?
定义:把方程中某一项改变符号后,从方程的一边移到另一边,这种变形叫作移项.
依据是等式的性质1
移项要变号!
例1:解方程:3x+5 = 5x-7.
解:移项,得
3x-5x = -7-5.
合并同类项,得
-2x = -12.
两边同除以-2,得
x = 6.
移项
合并同类项
系数化为1
步骤:
一元方程的解也叫作根.
【教材P98 例1】
练一练
解下列方程:
(1)8x=4x+1; (2)2-3x = 5x+10.
解:移项,得-3x-5x = 10-2.
合并同类项,得-8x = 8.
两边同除以-8,得x = -1.
解:移项,得8x-4x = 1.
合并同类项,得 4x = 1.
两边同除以4,得 x = .
注意:①方程的各项包括它前面的符号;
②移项时,不管是把某一项从左边移到右边还是从右边移到左边,都要变号.
例2:解方程:2(x-2)-3(4x-1) = 9(1-x).
思考:这个方程要怎么解?要先做什么?
先去括号.
解:去括号,得
2x-4-12x+3 = 9-9x.
移项,得
2x-12x+9x = 9+4-3.
合并同类项,得
-x = 10.
两边同除以-1,得
x = -10.
步骤:
去括号
移项
合并同类项
系数化为1
解一元一次方程:目标向 x = a 的形式转化.
【教材P99 例2】
随堂练习
1.下面的移项对不对 如果不对,错在哪里 应当怎样改正
(1)由9+x=7,得x=7+9;
(2)由5x=7-4x,得5x-4x=7;
(3)由2y-1=3y+6,得2y-3y=6-1.
【教材P99 练习 第1题】
不对,9移项没变号,改正:x=7-9.
不对,-4x移项没变号,改正:5x+4x=7.
不对,-1移项没变号,改正:2y-3y=6+1.
2.下面解方程的过程正确吗 请说明理由.
解方程:3(y-3)-5(1+y) = 7(y-1).
解:去括号,得 3y-3-5+5y = 7y-1.
移项,得 3y+5y-7y = -1+3-5.
合并同类项,得 y = -3.
【教材P99 练习 第2题】
解:不正确. 理由:①3(y-3)与7(y-1)去括号时漏乘常数项;②-5(1+y)去括号时弄错符号;③-5移项时未变号.
3.解下列方程:
(1)5x+21=7-2x; (2)2x- =- x+2;
(3)0.5(m+8)-0.6(2m-7)=1.9;(4)3(2y+1)=2(1+y)+3(y+3).
(1)解:移项,得5x+2x = 7-21.
合并同类项,得7x = -14.
两边同除以7,得x = -2.
【教材P100 练习 第3题】
3.解下列方程:
(1)5x+21=7-2x; (2)2x- =- x+2;
(3)0.5(m+8)-0.6(2m-7)=1.9;(4)3(2y+1)=2(1+y)+3(y+3).
【教材P100 练习 第3题】
(2)解:移项,得2x+ x = 2+ .
合并同类项,得 x = .
两边同除以 ,得x = 1.
3.解下列方程:
(1)5x+21=7-2x; (2)2x- =- x+2;
(3)0.5(m+8)-0.6(2m-7)=1.9;(4)3(2y+1)=2(1+y)+3(y+3).
【教材P100 练习 第3题】
(3)解:去括号,得0.5m+4-1.2m+4.2 = 1.9.
移项,得0.5m-1.2m = 1.9-4-4.2.
合并同类项,得-0.7m = -6.3.
两边同除以-0.7,得m = 9.
3.解下列方程:
(1)5x+21=7-2x; (2)2x- =- x+2;
(3)0.5(m+8)-0.6(2m-7)=1.9;(4)3(2y+1)=2(1+y)+3(y+3).
【教材P100 练习 第3题】
(4)解:去括号,得6y+3 = 2+2y+3y+9.
移项,得6y-2y-3y = 2+9-3.
合并同类项,得y = 8.
4.解方程:7(1-2x)+11(1-2x)=2x-1.
你有几种解法?
方法1:
解:去括号得7-14x+11-22x=2x-1
移项,得-14x-22x-2x=-1-7-11
合并同类项,得-38x=-19
系数化为1得x= .
方法2:
解:7(1-2x)+11(1-2x)=-(1-2x)
移项得7(1-2x)+11(1-2x)+(1-2x)=0
合并同类项得(7+11+1)(1-2x)=0
19(1-2x)=0
1-2x=0
移项,得-2x=0-1
化系数为1,得x= .
利用整体思想,叫作换元法。
1星题 基础练
知识点1 一元一次方程的概念
1.[2025·安庆月考]下列方程中是一元一次方程的是( )
C
A. B.
C. D.
2.[2024·阜阳期中]已知 是一元一次方程,则
的值为___.
1
知识点2 移项
3.[知识初练]如图,将方程
移项,令含有未知数
的项移到等号的____边,需要注意
的是移项要______,故“ ”处应填
写的是_____.
左
变号
4.将方程 移项,正确的是( )
D
A. B.
C. D.
5.(8分)判断下列方程的变形是否正确,如果不正确请改正.
(1)由得 ;
解:不正确. 改正:由得 .
(2)由得 ;
不正确. 改正:由得 .
(3)由得 ;
正确.
(4)由得 .
不正确. 改正:由得 .
知识点3 移项解一元一次方程(不含括号)
6.[知识初练]解方程 的一般步骤:
解:移项,得___________________,
合并同类项,得____________,
两边同除以 ,得______.
7.若的值是12,则 的值是___.
5
8.(8分)教材改编题 解方程:
(1) ;
解:移项,得,合并同类项,得 ,
两边同除以2,得 .
(2) .
解:移项,得 ,合并同类项,得
,两边同除以,得 .
知识点4 移项解一元一次方程(含括号)
9.[知识初练]解方程 的一般步骤:
解:去括号,得_____________________,
移项,得_____________________,
合并同类项,得_________,
两边同除以4,得______.
10.[2025年1月芜湖期末]将方程 去括号,
得________________.
11.(8分)教材改编题 解方程:
(1) ;
解:去括号,得 ,移项、合并同类项,得
,两边同除以,得 .
(2) .
解:去括号,得 ,移项、合并同类项,
得,两边同除以,得 .
2星题 中档练
12.易错题[2025年1月合肥期末] 方程
是关于的一元一次方程,则 ( )
B
A.2 B. C. D.
13.[2025年1月淮北期末]王涵同学在解关于 的方程
时,误将“”看成了“ ”,得到方程的解为
,那么原方程的解为( )
A
A. B. C. D.
14.创新题·新考法 规定一种新运算: ,若
,则 的值为( )
A
A. B.1 C.2 D.
15.若关于的方程的解比 的解小
8,则 的值为___.
1
16.(8分)解下列方程:
(1) ;
解:去括号,得 ,
移项,得 ,
合并同类项,得,系数化为1,得 .
(2) .
解:去中括号,得 ,
去小括号,得 ,移项、合并同类项,得
,两边同除以,得 .
17.(8分)[2025·上海模拟]解方程: .
解:去括号,得 .①
移项,得 .②
合并同类项,得 .③
两边同除以2,得
上述解答过程从哪一步开始出错?指出并写出正确的解答过程.
解:解答过程从第①步开始出错.正确的解答过程如下:去括
号,得 ,
移项,得,合并同类项,得 ,
两边同除以2,得 .
3星题 提升练
18.(8分)分类讨论思想先阅读下面的解题过程,然后解答后
面的问题.
解方程: .
解:当时,原方程可化为 ,
解得 ;
当时,原方程可化为 ,
解得 .
所以原方程的解是或 .
解方程: .
解:当时,原方程可化为,解得 ;
当时,原方程可化为,解得 .
所以原方程的解是或 .
课堂小结
解一元一次方程步骤:
去括号
移项
合并同类项
系数化为1
解一元一次方程:目标向 x = a 的形式转化.
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
