3.3.1几何问题与行程问题 课件(共38张PPT)
文档属性
| 名称 | 3.3.1几何问题与行程问题 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 21:04:17 | ||
图片预览









文档简介
(共38张PPT)
3.3.1几何问题与行程问题
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
3.3.1 几何问题与行程问题
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
上一部分我们学习了利用一元一次方程解决和、差、倍、分问题以及行程问题中的相遇问题。今天我们将重点学习几何问题和行程问题中的追及问题,这些问题在实际生活中也经常遇到,解决它们同样需要我们找出等量关系,列出方程求解。
学习目标
能运用一元一次方程解决与几何图形的周长、面积、体积相关的问题,掌握几何问题中常见的等量关系。
理解行程问题中追及问题的特点,能找出追及问题中的等量关系,列出方程并求解。
进一步体会方程思想在解决实际问题中的应用,提高分析和解决问题的能力。
知识点:几何问题
几何问题主要涉及几何图形的周长、面积、体积等计算,解决这类问题需要我们熟悉各种几何图形的相关公式,然后根据题目中的条件找出等量关系,列出方程。
常见几何图形的公式
长方形:
周长公式:\(C = 2 (é + )\)
面积公式:\(S = é \)
正方形:
周长公式:\(C = 4 è é \)
面积公式:\(S = è é è é \)
三角形:
面积公式:\(S=\frac{1}{2} é \)
圆:
周长公式:\(C = 2 r\)(\(r\)为半径)
面积公式:\(S = r \)
长方体:
体积公式:\(V = é é \)
正方体:
体积公式:\(V = ±é ±é ±é \)
例题解析
例 1:一个长方形的周长是 40 厘米,长比宽多 4 厘米,求这个长方形的长和宽。
解:审:已知长方形的周长是 40 厘米,长比宽多 4 厘米,求长和宽。
设:设长方形的宽为\(x\)厘米,则长为\((x + 4)\)厘米。
找:等量关系是 “长方形的周长 = 2×(长 + 宽)”。
列:根据等量关系,列出方程:\(2 (x + x + 4)=40\)。
解:解这个方程:\(
\begin{align*}
2 (2x + 4)&=40\\
4x + 8&=40\\
4x&=32\\
x&=8
\end{align*}
\)
则长方形的长为:\(x + 4 = 8 + 4 = 12\)(厘米)。
验:长方形的长是 12 厘米,宽是 8 厘米,周长为\(2 (12 + 8)=40\)厘米,且长比宽多 4 厘米,符合题意。
答:这个长方形的长是 12 厘米,宽是 8 厘米。
例 2:一个三角形的面积是 24 平方厘米,底是 8 厘米,求这个三角形的高。
解:审:已知三角形的面积是 24 平方厘米,底是 8 厘米,求高。
设:设这个三角形的高为\(h\)厘米。
找:等量关系是 “三角形的面积 =\(\frac{1}{2} é \)”。
列:根据等量关系,列出方程:\(\frac{1}{2} 8 h = 24\)。
解:解这个方程:\(
\begin{align*}
4h&=24\\
h&=6
\end{align*}
\)
验:三角形的底是 8 厘米,高是 6 厘米,面积为\(\frac{1}{2} 8 6 = 24\)平方厘米,符合题意。
答:这个三角形的高是 6 厘米。
例 3:一个长方体的体积是 120 立方厘米,长是 6 厘米,宽是 5 厘米,求这个长方体的高。
解:审:已知长方体的体积是 120 立方厘米,长是 6 厘米,宽是 5 厘米,求高。
设:设这个长方体的高为\(h\)厘米。
找:等量关系是 “长方体的体积 = 长 × 宽 × 高”。
列:根据等量关系,列出方程:\(6 5 h = 120\)。
解:解这个方程:\(
\begin{align*}
30h&=120\\
h&=4
\end{align*}
\)
验:长方体的长是 6 厘米,宽是 5 厘米,高是 4 厘米,体积为\(6 5 4 = 120\)立方厘米,符合题意。
答:这个长方体的高是 4 厘米。
例 4:把一个长为 10 厘米,宽为 8 厘米的长方形铁片,从四个角各剪去一个边长为\(x\)厘米的小正方形,再折成一个无盖的长方体盒子,已知这个盒子的容积是 48 立方厘米,求\(x\)的值。(厚度忽略不计)
解:审:长方形铁片长 10 厘米,宽 8 厘米,从四角剪去边长为\(x\)厘米的小正方形,折成无盖长方体盒子,容积 48 立方厘米,求\(x\)。
分析:折成的长方体盒子的长为\((10 - 2x)\)厘米,宽为\((8 - 2x)\)厘米,高为\(x\)厘米,容积 = 长 × 宽 × 高。
设:设小正方形的边长为\(x\)厘米。
找:等量关系是 “长方体盒子的容积 = 48 立方厘米”。
列:根据等量关系,列出方程:\((10 - 2x)(8 - 2x)x = 48\)。
解:展开方程:\(
\begin{align*}
(80 - 20x - 16x + 4x )x&=48\\
(80 - 36x + 4x )x&=48\\
4x - 36x + 80x - 48&=0\\
x - 9x + 20x - 12&=0
\end{align*}
\)
尝试因式分解或代入数值验证,可得\(x = 1\)是方程的解(\(x = 3\)时,宽为\(8 - 2 3 = 2\),长为\(10 - 2 3 = 4\),容积为\(4 2 3 = 24 48\);\(x = 2\)时,长为\(10 - 4 = 6\),宽为\(8 - 4 = 4\),容积为\(6 4 2 = 48\),所以\(x = 2\)也是解,需结合实际,\(x\)不能过大,否则长和宽为负数,所以\(x = 1\)和\(x = 2\)均有可能,经检验都符合题意)。
验:当\(x = 1\)时,长为\(10 - 2 1 = 8\)厘米,宽为\(8 - 2 1 = 6\)厘米,高为 1 厘米,容积为\(8 6 1 = 48\)立方厘米;当\(x = 2\)时,长为 6 厘米,宽为 4 厘米,高为 2 厘米,容积为\(6 4 2 = 48\)立方厘米,均符合题意。
答:\(x\)的值为 1 厘米或 2 厘米。
知识点:行程问题中的追及问题
追及问题是行程问题中的另一种重要类型,指两个物体同向运动,速度快的物体从后面追上速度慢的物体的问题。
常见等量关系
路程 = 速度 × 时间;
追及路程 = 速度快的物体所走的路程 - 速度慢的物体所走的路程;
追及时间 = 追及路程 ÷(快速度 - 慢速度)。
例题解析
例 5:甲、乙两人在同一地点,甲骑自行车,乙步行。如果乙先出发 10 分钟,甲骑自行车去追赶,甲每分钟行 250 米,乙每分钟走 80 米,甲出发后多少分钟能追上乙?
解:审:甲、乙同一地点,乙先出发 10 分钟,甲骑车追,甲速 250 米 / 分钟,乙速 80 米 / 分钟,求甲出发后追上乙的时间。
分析:乙先出发 10 分钟,所走路程为\(80 10 = 800\)米,这就是追及路程。
设:设甲出发后\(x\)分钟能追上乙。
找:等量关系是 “甲走的路程 = 乙先走路程 + 乙后走路程”。
列:根据等量关系,列出方程:\(250x = 80 10 + 80x\)。
解:解这个方程:\(
\begin{align*}
250x - 80x&=800\\
170x&=800\\
x&=\frac{80}{17}\approx4.71
\end{align*}
\)
验:甲出发\(\frac{80}{17}\)分钟走的路程为\(250 \frac{80}{17}=\frac{20000}{17}\)米,乙总共走的路程为\(80 (10 + \frac{80}{17})=80 \frac{250}{17}=\frac{20000}{17}\)米,两者相等,符合题意。
答:甲出发后\(\frac{80}{17}\)分钟能追上乙。
例 6:A、B 两地相距 200 千米,甲车从 A 地出发,每小时行驶 60 千米,乙车从 B 地出发,每小时行驶 40 千米,两车同时同向行驶,甲车在乙车后面,经过多少小时甲车追上乙车?
解:审:A、B 两地相距 200 千米,甲从 A 出发,速 60 千米 / 小时,乙从 B 出发,速 40 千米 / 小时,同向行驶,甲在乙后,求甲追上乙的时间。
分析:追及路程就是 A、B 两地的距离 200 千米。
设:设经过\(x\)小时甲车追上乙车。
找:等量关系是 “甲车行驶的路程 = 乙车行驶的路程 + 200 千米”。
列:根据等量关系,列出方程:\(60x = 40x + 200\)。
解:解这个方程:\(
\begin{align*}
60x - 40x&=200\\
20x&=200\\
x&=10
\end{align*}
\)
验:10 小时后,甲车行驶\(60 10 = 600\)千米,乙车行驶\(40 10 = 400\)千米,\(600 = 400 + 200\),符合题意。
答:经过 10 小时甲车追上乙车。
例 7:甲、乙两人在环形跑道上跑步,跑道一圈长 400 米,甲每秒跑 6 米,乙每秒跑 4 米。如果两人同时同地同向出发,经过多少秒甲首次追上乙?
解:审:环形跑道长 400 米,甲速 6 米 / 秒,乙速 4 米 / 秒,同时同地同向出发,求甲首次追上乙的时间。
分析:甲首次追上乙时,甲比乙多跑了一圈,即 400 米,这是追及路程。
设:设经过\(x\)秒甲首次追上乙。
找:等量关系是 “甲跑的路程 - 乙跑的路程 = 400 米”。
列:根据等量关系,列出方程:\(6x - 4x = 400\)。
解:解这个方程:\(
\begin{align*}
2x&=400\\
x&=200
\end{align*}
\)
验:200 秒后,甲跑了\(6 200 = 1200\)米,乙跑了\(4 200 = 800\)米,\(1200 - 800 = 400\)米,符合题意。
答:经过 200 秒甲首次追上乙。
小练习
一个长方形的周长是 30 厘米,长是宽的 2 倍,求这个长方形的长和宽。
一个圆的面积是\(25 \)平方厘米,求这个圆的半径。
一个正方体的表面积是 54 平方厘米,求这个正方体的棱长。(正方体表面积公式:\(S = 6 ±é \))
甲、乙两人相距 10 千米,甲在前,乙在后,甲每小时走 5 千米,乙每小时走 7 千米,两人同时同向出发,乙经过多少小时追上甲?
一列火车长 200 米,以每秒 20 米的速度通过一座长 1000 米的大桥,从车头上桥到车尾离桥一共需要多少秒?
思考讨论
解决几何问题时,如何准确找到等量关系?
解决几何问题,首先要明确涉及的几何图形类型,回忆其周长、面积、体积等公式。然后根据题目中给出的条件,如 “周长相等”“面积增加了多少”“体积是多少” 等,结合图形的变化情况,确定等量关系。例如,在折叠问题中,折叠前后图形的某些边的长度或面积是不变的,这就是重要的等量关系。
追及问题和相遇问题在等量关系上有什么不同?
相遇问题中,等量关系通常是 “总路程 = 甲走的路程 + 乙走的路程”;而追及问题中,等量关系通常是 “快者走的路程 = 慢者走的路程 + 追及路程”(追及路程是两者开始时的距离)。两者的运动方向不同,相遇是相向而行,追及是同向而行,这导致了等量关系的差异。
课堂小结
几何问题:关键是熟悉各种几何图形的周长、面积、体积公式,根据题目条件找出与这些公式相关的等量关系,列出方程求解。常见的有长方形、正方形、三角形、圆等平面图形的问题,以及长方体、正方体等立体图形的问题。
追及问题:重点是确定追及路程,即开始时两者之间的距离,等量关系通常是快者行驶的路程等于慢者行驶的路程加上追及路程。要注意区分同向行驶的情况,准确计算两者的路程差。
无论是几何问题还是追及问题,都需要我们认真审题,分析数量关系,找出等量关系,这是列方程解决问题的核心。
课后作业
一个长方形的长比宽多 3 厘米,面积是 40 平方厘米,求这个长方形的长和宽。
一个梯形的上底是 5 厘米,下底是 9 厘米,面积是 42 平方厘米,求这个梯形的高。(梯形面积公式:\(S=\frac{1}{2} ( + ) é \))
甲、乙两车从同一地点出发,甲车先出发 2 小时,甲车每小时行驶 40 千米,乙车每小时行驶 60 千米,乙车出发后经过多少小时追上甲车?
一座大桥长 1500 米,一列火车从桥上通过,测得火车从开始上桥到完全下桥共用了 150 秒,整列火车完全在桥上的时间为 100 秒,求火车的长度和速度。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
复习回顾
常见几何体的体积、面积公式:
(1)长方体的体积=长×宽×高;
(2)正方体的体积=棱长×棱长×棱长;
(3)圆柱的体积=底面积×高;
(4)长方形的面积=长×宽;
(5)正方形的面积=边长×边长;
(6)梯形的面积= (上底+下底)×高.
探索新知
例1:如图,李明同学从一张正方形纸片上剪去一张宽为4cm的长方形纸条,再从剩下的长方形纸片上剪去一张宽5cm的长方形纸条.如果两次剪下的长方形纸条面积正好相等,那么原正方形的边长为多少
4
5
(单位:cm)
【教材P103 例1】
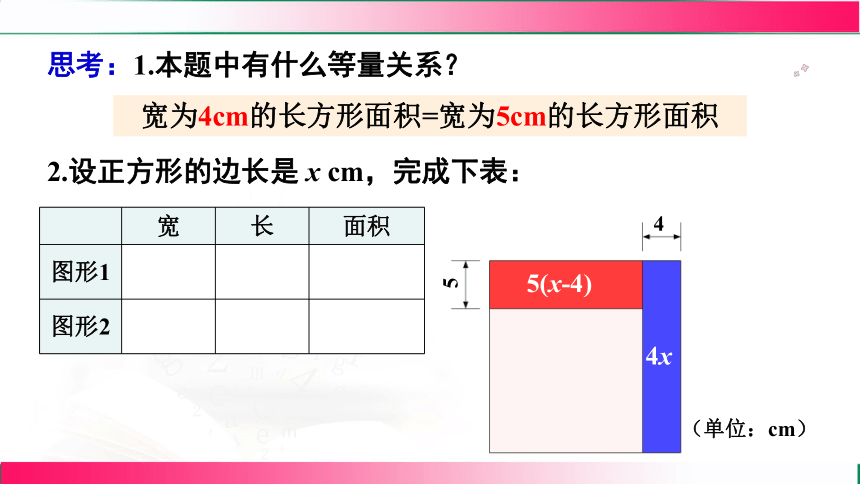
思考:1.本题中有什么等量关系?
4
5
(单位:cm)
宽为4cm的长方形面积=宽为5cm的长方形面积
2.设正方形的边长是 x cm,完成下表:
宽 长 面积
图形1 4 x 4x
图形2 5 x-4 5(x-4)
4x
5(x-4)
4
5
(单位:cm)
解:设正方形的边长是 x cm,根据题意,得
4x = 5(x-4).
解方程,得x=20.
答:原正方形的边长为20cm.
4x
5(x-4)
宽为4cm的长方形面积=宽为5cm的长方形面积
形积变化中的等量关系
①形状发生了变化,体积/面积不变. 其相等关系是:
变化前图形的体积/面积=变化后图形的体积/面积
②形状、面积发生了变化,周长不变. 其相等关系是:
变化前图形的周长=变化后图形的周长
③形状、体积不同,面积相同.根据题意找出面积之间的关系,即相等关系.
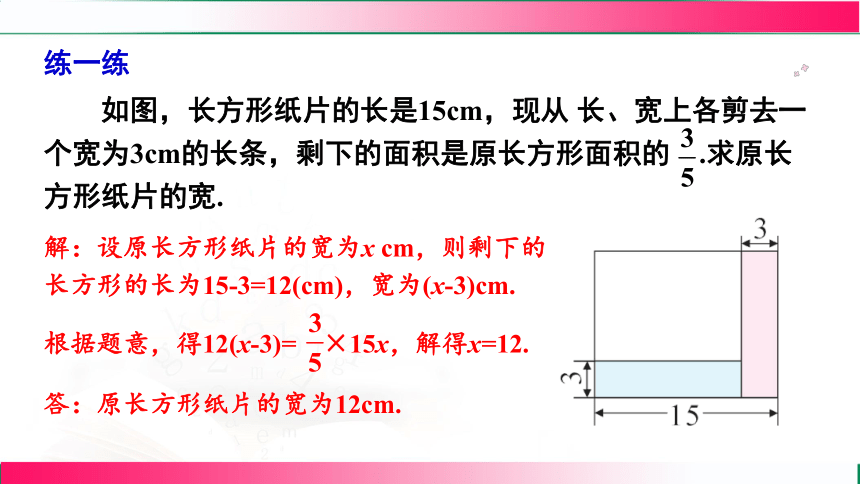
如图,长方形纸片的长是15cm,现从 长、宽上各剪去一个宽为3cm的长条,剩下的面积是原长方形面积的 .求原长方形纸片的宽.
练一练
解:设原长方形纸片的宽为x cm,则剩下的长方形的长为15-3=12(cm),宽为(x-3)cm.
根据题意,得12(x-3)= ×15x,解得x=12.
答:原长方形纸片的宽为12cm.
例2:某县举办越野赛. 选手从起点出发,先沿着山区公路跑步到达补给站,再登山到达比赛终点. 张老师参加了这个比赛,他的相关数据如下表:
总距离/km 跑步平均速度/km·h-1 登山平均速度/km·h-1
8.2 10 3
已知张老师在补给站休息了10min,用时1.5h完成了比赛.求补给站与起点的距离.
8.2km
起点
补给站
终点
跑步距离+登山距离=总距离
【教材P103 例2】
8.2km
起点
补给站
终点
x km
8.2-x km
跑步时间+登山时间=总用时-休息时间
解:设补给站离起点x km. 根据题意,得
注意单位换算!
解方程,得x=6.
答:补给站与起点的距离为6km.
交流:运用一元一次方程解决实际问题的基本过程是怎样的?
实际问题
找等量关系,列方程
数学问题
(一元一次方程)
解方程
数学问题的解
(一元一次方程的解)
检验
实际问题的答案
“读万卷书,行万里路”,经历是最好的学习,研学是最美的相遇. 11月中旬七年级的学生开启了以“溯源千年谯城·浸润万缕药香”为主题的亳州研学之旅. 已知①号车和②号车同时从合肥出发沿同一路线开往亳州,①号车的行驶速度是 80km/h,②号车的行驶速度是72km/h,①号车比②号车早到
h,求合肥与亳州相距多少千米
练一练
解:设合肥与亳州相距x km.
根据题意,得 ,解得x=320.
答:合肥与亳州相距320km.
归纳总结
列方程解应用题的一般步骤如下:
⑴弄清题意和题中的数量关系,用字母(如x,y)表示问题涉及的未知数;
⑵分析题意,找出等量关系(可借助示意图、表格等);
⑶根据等量关系,列出需要的代数式,并列出方程;
⑷解这个方程,求出未知数的值;
⑸检查所得的值是否正确和符合实际情形,并写出答案(包括单位).
随堂练习
1.列方程,解下列各题:
(1)一种小麦磨成面粉,出粉率为80%(即20%成为麸子).为了得到4500 kg面粉,至少需要多少小麦
【教材P104 练习】
解:设至少需要x kg小麦.
根据题意,得x·80% = 4500.
解方程,得x=5625.
答:至少需要 5625 kg小麦.
(2)甲厂有钢材432t,乙厂有钢材96t.如果每天从甲厂运出20t,乙厂运出4t,几天后甲厂剩余的钢材是乙厂的2倍
解:设x天后,甲厂剩余的钢材是乙厂的2倍.
根据题意,得432-20x=2(96-4x).
解方程,得x=20.
答:20天后,甲厂剩余的钢材是乙厂的2倍.
(3)甲、乙两地相距180km.一人骑自行车从甲地出发,每小时骑行15km.另一人骑摩托车从乙地同时出发.两人相向而行.已知摩托车车速是自行车车速的3倍.多少时间后两人相遇?
解:设x h后两人相遇.
根据题意,得x(15+15×3)=180.
解方程,得x=3.
答:3h后两人相遇.
2.有一根合金圆柱,底面半径为1 dm,高为64 cm,若将其锻造成长方体工件,使长方体工件的长为20π cm,高为32 cm,则长方体工件的宽是多少
解:设长方体工件的宽是x cm.
1 dm=10 cm,
根据题意,得π×102×64=20π×32x,
解得x=10.
答:长方体工件的宽是10cm.
3. 甲、乙两人从相距200km的两地相向而行,甲乘汽车每小时行60km,乙骑自行车每小时行20km. 如果乙先行2h,那么甲出发多长时间后两人相遇
解:设甲出发x h后两人相遇.
根据题意,得60x+20(x+2)=200,解得x=2.
答:甲出发2h后两人相遇.
1.为增加展示作品的质感,需要准备一些相框进行展示,现
将一根木条进行切割制作相框,原计划制作正方形的相框,
现改为制作长方形的相框,若新的长方形相框的宽比原正方
形相框的边长少 ,新的长方形相框的长等于原正方形相
框的边长,且新的长方形相框需要用 长的木条,若设
原正方形相框的边长为 ,则可列方程为______________
_____.
2.为增加展示作品的美感,学校打算用彩纸包装相框.如图,
将一张正方形彩纸剪下一个宽为 的长条后,再从剩下的
长方形彩纸上剪去一个宽为 的长条.如果两次剪下的长
条面积相等,那么每一个长条的面积为_____ .
150
3.(8分)为增加展示现场的氛围感,学校决定购买彩色的地垫,
进行地面装饰.如图,其中一部分图案为用8个相同的小长方
形拼成的大长方形,求1个小长方形的面积.
解:设1个小长方形的宽为 ,根
据题图可知1个小长方形的长为
,则 ,解得
,则
答:1个小长方形的面积为 .
知识点2 行程问题
4.[2025年1月滁州期末]一艘轮船在, 两个码头之间航
行,顺水航行需,逆水航行需.已知水流速度为 ,
求轮船在静水中的航行速度.若设轮船在静水中的航行速度为
,则可列一元一次方程为( )
B
A. B.
C. D.
5.[2025年1月马鞍山期末]已知学校距离敬老院 .小
明和小刚两人从学校出发去敬老院送水果,小明带着水果先
走了,然后小刚才出发.若小明每分钟行 ,小刚
每分钟行,则小刚用___ 可以追上小明.
5
6.(8分)[2024·合肥模拟]小刚和小强从, 两地同时出发,
小刚骑自行车,小强步行,沿同一条路线相向匀速而行,出
发后两人相遇,相遇时小刚比小强多行进 ,相遇
后小刚到达 地.两人的行进速度分别是多少?
解:设小刚的行进速度为 ,
则相遇时小刚走了,小强走了 ,
由题意,得,解得 ,
则小强的行进速度为
答:小刚的行进速度是 ,小强的行进速度是
.
2星题 中档练
7.数学文化 我国古代名著《九章算术》中有一个问题,原文:
“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫
雁俱起,问何日相逢?”译文:野鸭从南海出发,7天后到达
北海;大雁从北海出发,9天后到达南海,今野鸭和大雁分
别从南海和北海同时出发,几天后相遇?设 天后相遇,可
列方程为( )
B
A. B.
C. D.
8.匀速行驶的动车经过一座大桥时,动车从车头上桥到车头
离桥共需要 ;而从动车车尾上桥开始到车头离桥结束,
整列动车完全在桥上的时间是 .已知该列动车长为
,则动车经过的这座大桥的长度为_______ .
9.(8分) 教材改编题 [2025· 安庆月考] 将一个底面内径是
,高是 的圆柱体桶内装满水,再将桶内的水倒
入一个底面内径是,高是 的圆柱体玻璃杯内,
能否完全装下?若装不下,则桶内还有多高的水?若没装满,
求杯内水面的高度.
解:不能完全装下.由题意得,水的体积为
.圆柱体玻璃杯的容积为
.因为 ,即水的体
积大于圆柱体玻璃杯的容积,所以不能完全装下.设桶内还有
高的水,由题意,得 ,解得
.故桶内还有 高的水.
10.(12分)真实情境如图是两张不同类型火车(“ 次”表
示动车,“ 次”表示高铁)的车票的部分信息.
(1)根据车票中的信息填空:该列动车和高铁是____
(填“相”或“同”)向而行,并且动车比高铁发车____
(填“早”或“晚”);
同
早
(2)已知该列动车和高铁的平均速度分别为 ,
,两列火车的长度不计,高铁比动车早到 ,求
, 两地之间的距离;
解:设,两地之间的距离为 .
根据题意得,解得 .
答:,两地之间的距离为 .
(3)在(2)的条件下,若
高铁到达 地后停止运
动,求高铁出发多少
小时后两车相距 .
设高铁出发后两车相距 ,
①当高铁还未追上动车时, ,解
得;②当高铁追上动车后, ,
解得;③当高铁到达 地,动车还未到达时,
,解得 .
答:高铁出发或 或
后两车相距 .
课堂小结
用一元一次方程解决实际问题的基本过程
实际问题
找等量关系,列方程
数学问题
(一元一次方程)
解方程
数学问题的解
(一元一次方程的解)
检验
实际问题的答案
谢谢观看!
3.3.1几何问题与行程问题
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
3.3.1 几何问题与行程问题
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
上一部分我们学习了利用一元一次方程解决和、差、倍、分问题以及行程问题中的相遇问题。今天我们将重点学习几何问题和行程问题中的追及问题,这些问题在实际生活中也经常遇到,解决它们同样需要我们找出等量关系,列出方程求解。
学习目标
能运用一元一次方程解决与几何图形的周长、面积、体积相关的问题,掌握几何问题中常见的等量关系。
理解行程问题中追及问题的特点,能找出追及问题中的等量关系,列出方程并求解。
进一步体会方程思想在解决实际问题中的应用,提高分析和解决问题的能力。
知识点:几何问题
几何问题主要涉及几何图形的周长、面积、体积等计算,解决这类问题需要我们熟悉各种几何图形的相关公式,然后根据题目中的条件找出等量关系,列出方程。
常见几何图形的公式
长方形:
周长公式:\(C = 2 (é + )\)
面积公式:\(S = é \)
正方形:
周长公式:\(C = 4 è é \)
面积公式:\(S = è é è é \)
三角形:
面积公式:\(S=\frac{1}{2} é \)
圆:
周长公式:\(C = 2 r\)(\(r\)为半径)
面积公式:\(S = r \)
长方体:
体积公式:\(V = é é \)
正方体:
体积公式:\(V = ±é ±é ±é \)
例题解析
例 1:一个长方形的周长是 40 厘米,长比宽多 4 厘米,求这个长方形的长和宽。
解:审:已知长方形的周长是 40 厘米,长比宽多 4 厘米,求长和宽。
设:设长方形的宽为\(x\)厘米,则长为\((x + 4)\)厘米。
找:等量关系是 “长方形的周长 = 2×(长 + 宽)”。
列:根据等量关系,列出方程:\(2 (x + x + 4)=40\)。
解:解这个方程:\(
\begin{align*}
2 (2x + 4)&=40\\
4x + 8&=40\\
4x&=32\\
x&=8
\end{align*}
\)
则长方形的长为:\(x + 4 = 8 + 4 = 12\)(厘米)。
验:长方形的长是 12 厘米,宽是 8 厘米,周长为\(2 (12 + 8)=40\)厘米,且长比宽多 4 厘米,符合题意。
答:这个长方形的长是 12 厘米,宽是 8 厘米。
例 2:一个三角形的面积是 24 平方厘米,底是 8 厘米,求这个三角形的高。
解:审:已知三角形的面积是 24 平方厘米,底是 8 厘米,求高。
设:设这个三角形的高为\(h\)厘米。
找:等量关系是 “三角形的面积 =\(\frac{1}{2} é \)”。
列:根据等量关系,列出方程:\(\frac{1}{2} 8 h = 24\)。
解:解这个方程:\(
\begin{align*}
4h&=24\\
h&=6
\end{align*}
\)
验:三角形的底是 8 厘米,高是 6 厘米,面积为\(\frac{1}{2} 8 6 = 24\)平方厘米,符合题意。
答:这个三角形的高是 6 厘米。
例 3:一个长方体的体积是 120 立方厘米,长是 6 厘米,宽是 5 厘米,求这个长方体的高。
解:审:已知长方体的体积是 120 立方厘米,长是 6 厘米,宽是 5 厘米,求高。
设:设这个长方体的高为\(h\)厘米。
找:等量关系是 “长方体的体积 = 长 × 宽 × 高”。
列:根据等量关系,列出方程:\(6 5 h = 120\)。
解:解这个方程:\(
\begin{align*}
30h&=120\\
h&=4
\end{align*}
\)
验:长方体的长是 6 厘米,宽是 5 厘米,高是 4 厘米,体积为\(6 5 4 = 120\)立方厘米,符合题意。
答:这个长方体的高是 4 厘米。
例 4:把一个长为 10 厘米,宽为 8 厘米的长方形铁片,从四个角各剪去一个边长为\(x\)厘米的小正方形,再折成一个无盖的长方体盒子,已知这个盒子的容积是 48 立方厘米,求\(x\)的值。(厚度忽略不计)
解:审:长方形铁片长 10 厘米,宽 8 厘米,从四角剪去边长为\(x\)厘米的小正方形,折成无盖长方体盒子,容积 48 立方厘米,求\(x\)。
分析:折成的长方体盒子的长为\((10 - 2x)\)厘米,宽为\((8 - 2x)\)厘米,高为\(x\)厘米,容积 = 长 × 宽 × 高。
设:设小正方形的边长为\(x\)厘米。
找:等量关系是 “长方体盒子的容积 = 48 立方厘米”。
列:根据等量关系,列出方程:\((10 - 2x)(8 - 2x)x = 48\)。
解:展开方程:\(
\begin{align*}
(80 - 20x - 16x + 4x )x&=48\\
(80 - 36x + 4x )x&=48\\
4x - 36x + 80x - 48&=0\\
x - 9x + 20x - 12&=0
\end{align*}
\)
尝试因式分解或代入数值验证,可得\(x = 1\)是方程的解(\(x = 3\)时,宽为\(8 - 2 3 = 2\),长为\(10 - 2 3 = 4\),容积为\(4 2 3 = 24 48\);\(x = 2\)时,长为\(10 - 4 = 6\),宽为\(8 - 4 = 4\),容积为\(6 4 2 = 48\),所以\(x = 2\)也是解,需结合实际,\(x\)不能过大,否则长和宽为负数,所以\(x = 1\)和\(x = 2\)均有可能,经检验都符合题意)。
验:当\(x = 1\)时,长为\(10 - 2 1 = 8\)厘米,宽为\(8 - 2 1 = 6\)厘米,高为 1 厘米,容积为\(8 6 1 = 48\)立方厘米;当\(x = 2\)时,长为 6 厘米,宽为 4 厘米,高为 2 厘米,容积为\(6 4 2 = 48\)立方厘米,均符合题意。
答:\(x\)的值为 1 厘米或 2 厘米。
知识点:行程问题中的追及问题
追及问题是行程问题中的另一种重要类型,指两个物体同向运动,速度快的物体从后面追上速度慢的物体的问题。
常见等量关系
路程 = 速度 × 时间;
追及路程 = 速度快的物体所走的路程 - 速度慢的物体所走的路程;
追及时间 = 追及路程 ÷(快速度 - 慢速度)。
例题解析
例 5:甲、乙两人在同一地点,甲骑自行车,乙步行。如果乙先出发 10 分钟,甲骑自行车去追赶,甲每分钟行 250 米,乙每分钟走 80 米,甲出发后多少分钟能追上乙?
解:审:甲、乙同一地点,乙先出发 10 分钟,甲骑车追,甲速 250 米 / 分钟,乙速 80 米 / 分钟,求甲出发后追上乙的时间。
分析:乙先出发 10 分钟,所走路程为\(80 10 = 800\)米,这就是追及路程。
设:设甲出发后\(x\)分钟能追上乙。
找:等量关系是 “甲走的路程 = 乙先走路程 + 乙后走路程”。
列:根据等量关系,列出方程:\(250x = 80 10 + 80x\)。
解:解这个方程:\(
\begin{align*}
250x - 80x&=800\\
170x&=800\\
x&=\frac{80}{17}\approx4.71
\end{align*}
\)
验:甲出发\(\frac{80}{17}\)分钟走的路程为\(250 \frac{80}{17}=\frac{20000}{17}\)米,乙总共走的路程为\(80 (10 + \frac{80}{17})=80 \frac{250}{17}=\frac{20000}{17}\)米,两者相等,符合题意。
答:甲出发后\(\frac{80}{17}\)分钟能追上乙。
例 6:A、B 两地相距 200 千米,甲车从 A 地出发,每小时行驶 60 千米,乙车从 B 地出发,每小时行驶 40 千米,两车同时同向行驶,甲车在乙车后面,经过多少小时甲车追上乙车?
解:审:A、B 两地相距 200 千米,甲从 A 出发,速 60 千米 / 小时,乙从 B 出发,速 40 千米 / 小时,同向行驶,甲在乙后,求甲追上乙的时间。
分析:追及路程就是 A、B 两地的距离 200 千米。
设:设经过\(x\)小时甲车追上乙车。
找:等量关系是 “甲车行驶的路程 = 乙车行驶的路程 + 200 千米”。
列:根据等量关系,列出方程:\(60x = 40x + 200\)。
解:解这个方程:\(
\begin{align*}
60x - 40x&=200\\
20x&=200\\
x&=10
\end{align*}
\)
验:10 小时后,甲车行驶\(60 10 = 600\)千米,乙车行驶\(40 10 = 400\)千米,\(600 = 400 + 200\),符合题意。
答:经过 10 小时甲车追上乙车。
例 7:甲、乙两人在环形跑道上跑步,跑道一圈长 400 米,甲每秒跑 6 米,乙每秒跑 4 米。如果两人同时同地同向出发,经过多少秒甲首次追上乙?
解:审:环形跑道长 400 米,甲速 6 米 / 秒,乙速 4 米 / 秒,同时同地同向出发,求甲首次追上乙的时间。
分析:甲首次追上乙时,甲比乙多跑了一圈,即 400 米,这是追及路程。
设:设经过\(x\)秒甲首次追上乙。
找:等量关系是 “甲跑的路程 - 乙跑的路程 = 400 米”。
列:根据等量关系,列出方程:\(6x - 4x = 400\)。
解:解这个方程:\(
\begin{align*}
2x&=400\\
x&=200
\end{align*}
\)
验:200 秒后,甲跑了\(6 200 = 1200\)米,乙跑了\(4 200 = 800\)米,\(1200 - 800 = 400\)米,符合题意。
答:经过 200 秒甲首次追上乙。
小练习
一个长方形的周长是 30 厘米,长是宽的 2 倍,求这个长方形的长和宽。
一个圆的面积是\(25 \)平方厘米,求这个圆的半径。
一个正方体的表面积是 54 平方厘米,求这个正方体的棱长。(正方体表面积公式:\(S = 6 ±é \))
甲、乙两人相距 10 千米,甲在前,乙在后,甲每小时走 5 千米,乙每小时走 7 千米,两人同时同向出发,乙经过多少小时追上甲?
一列火车长 200 米,以每秒 20 米的速度通过一座长 1000 米的大桥,从车头上桥到车尾离桥一共需要多少秒?
思考讨论
解决几何问题时,如何准确找到等量关系?
解决几何问题,首先要明确涉及的几何图形类型,回忆其周长、面积、体积等公式。然后根据题目中给出的条件,如 “周长相等”“面积增加了多少”“体积是多少” 等,结合图形的变化情况,确定等量关系。例如,在折叠问题中,折叠前后图形的某些边的长度或面积是不变的,这就是重要的等量关系。
追及问题和相遇问题在等量关系上有什么不同?
相遇问题中,等量关系通常是 “总路程 = 甲走的路程 + 乙走的路程”;而追及问题中,等量关系通常是 “快者走的路程 = 慢者走的路程 + 追及路程”(追及路程是两者开始时的距离)。两者的运动方向不同,相遇是相向而行,追及是同向而行,这导致了等量关系的差异。
课堂小结
几何问题:关键是熟悉各种几何图形的周长、面积、体积公式,根据题目条件找出与这些公式相关的等量关系,列出方程求解。常见的有长方形、正方形、三角形、圆等平面图形的问题,以及长方体、正方体等立体图形的问题。
追及问题:重点是确定追及路程,即开始时两者之间的距离,等量关系通常是快者行驶的路程等于慢者行驶的路程加上追及路程。要注意区分同向行驶的情况,准确计算两者的路程差。
无论是几何问题还是追及问题,都需要我们认真审题,分析数量关系,找出等量关系,这是列方程解决问题的核心。
课后作业
一个长方形的长比宽多 3 厘米,面积是 40 平方厘米,求这个长方形的长和宽。
一个梯形的上底是 5 厘米,下底是 9 厘米,面积是 42 平方厘米,求这个梯形的高。(梯形面积公式:\(S=\frac{1}{2} ( + ) é \))
甲、乙两车从同一地点出发,甲车先出发 2 小时,甲车每小时行驶 40 千米,乙车每小时行驶 60 千米,乙车出发后经过多少小时追上甲车?
一座大桥长 1500 米,一列火车从桥上通过,测得火车从开始上桥到完全下桥共用了 150 秒,整列火车完全在桥上的时间为 100 秒,求火车的长度和速度。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
复习回顾
常见几何体的体积、面积公式:
(1)长方体的体积=长×宽×高;
(2)正方体的体积=棱长×棱长×棱长;
(3)圆柱的体积=底面积×高;
(4)长方形的面积=长×宽;
(5)正方形的面积=边长×边长;
(6)梯形的面积= (上底+下底)×高.
探索新知
例1:如图,李明同学从一张正方形纸片上剪去一张宽为4cm的长方形纸条,再从剩下的长方形纸片上剪去一张宽5cm的长方形纸条.如果两次剪下的长方形纸条面积正好相等,那么原正方形的边长为多少
4
5
(单位:cm)
【教材P103 例1】
思考:1.本题中有什么等量关系?
4
5
(单位:cm)
宽为4cm的长方形面积=宽为5cm的长方形面积
2.设正方形的边长是 x cm,完成下表:
宽 长 面积
图形1 4 x 4x
图形2 5 x-4 5(x-4)
4x
5(x-4)
4
5
(单位:cm)
解:设正方形的边长是 x cm,根据题意,得
4x = 5(x-4).
解方程,得x=20.
答:原正方形的边长为20cm.
4x
5(x-4)
宽为4cm的长方形面积=宽为5cm的长方形面积
形积变化中的等量关系
①形状发生了变化,体积/面积不变. 其相等关系是:
变化前图形的体积/面积=变化后图形的体积/面积
②形状、面积发生了变化,周长不变. 其相等关系是:
变化前图形的周长=变化后图形的周长
③形状、体积不同,面积相同.根据题意找出面积之间的关系,即相等关系.
如图,长方形纸片的长是15cm,现从 长、宽上各剪去一个宽为3cm的长条,剩下的面积是原长方形面积的 .求原长方形纸片的宽.
练一练
解:设原长方形纸片的宽为x cm,则剩下的长方形的长为15-3=12(cm),宽为(x-3)cm.
根据题意,得12(x-3)= ×15x,解得x=12.
答:原长方形纸片的宽为12cm.
例2:某县举办越野赛. 选手从起点出发,先沿着山区公路跑步到达补给站,再登山到达比赛终点. 张老师参加了这个比赛,他的相关数据如下表:
总距离/km 跑步平均速度/km·h-1 登山平均速度/km·h-1
8.2 10 3
已知张老师在补给站休息了10min,用时1.5h完成了比赛.求补给站与起点的距离.
8.2km
起点
补给站
终点
跑步距离+登山距离=总距离
【教材P103 例2】
8.2km
起点
补给站
终点
x km
8.2-x km
跑步时间+登山时间=总用时-休息时间
解:设补给站离起点x km. 根据题意,得
注意单位换算!
解方程,得x=6.
答:补给站与起点的距离为6km.
交流:运用一元一次方程解决实际问题的基本过程是怎样的?
实际问题
找等量关系,列方程
数学问题
(一元一次方程)
解方程
数学问题的解
(一元一次方程的解)
检验
实际问题的答案
“读万卷书,行万里路”,经历是最好的学习,研学是最美的相遇. 11月中旬七年级的学生开启了以“溯源千年谯城·浸润万缕药香”为主题的亳州研学之旅. 已知①号车和②号车同时从合肥出发沿同一路线开往亳州,①号车的行驶速度是 80km/h,②号车的行驶速度是72km/h,①号车比②号车早到
h,求合肥与亳州相距多少千米
练一练
解:设合肥与亳州相距x km.
根据题意,得 ,解得x=320.
答:合肥与亳州相距320km.
归纳总结
列方程解应用题的一般步骤如下:
⑴弄清题意和题中的数量关系,用字母(如x,y)表示问题涉及的未知数;
⑵分析题意,找出等量关系(可借助示意图、表格等);
⑶根据等量关系,列出需要的代数式,并列出方程;
⑷解这个方程,求出未知数的值;
⑸检查所得的值是否正确和符合实际情形,并写出答案(包括单位).
随堂练习
1.列方程,解下列各题:
(1)一种小麦磨成面粉,出粉率为80%(即20%成为麸子).为了得到4500 kg面粉,至少需要多少小麦
【教材P104 练习】
解:设至少需要x kg小麦.
根据题意,得x·80% = 4500.
解方程,得x=5625.
答:至少需要 5625 kg小麦.
(2)甲厂有钢材432t,乙厂有钢材96t.如果每天从甲厂运出20t,乙厂运出4t,几天后甲厂剩余的钢材是乙厂的2倍
解:设x天后,甲厂剩余的钢材是乙厂的2倍.
根据题意,得432-20x=2(96-4x).
解方程,得x=20.
答:20天后,甲厂剩余的钢材是乙厂的2倍.
(3)甲、乙两地相距180km.一人骑自行车从甲地出发,每小时骑行15km.另一人骑摩托车从乙地同时出发.两人相向而行.已知摩托车车速是自行车车速的3倍.多少时间后两人相遇?
解:设x h后两人相遇.
根据题意,得x(15+15×3)=180.
解方程,得x=3.
答:3h后两人相遇.
2.有一根合金圆柱,底面半径为1 dm,高为64 cm,若将其锻造成长方体工件,使长方体工件的长为20π cm,高为32 cm,则长方体工件的宽是多少
解:设长方体工件的宽是x cm.
1 dm=10 cm,
根据题意,得π×102×64=20π×32x,
解得x=10.
答:长方体工件的宽是10cm.
3. 甲、乙两人从相距200km的两地相向而行,甲乘汽车每小时行60km,乙骑自行车每小时行20km. 如果乙先行2h,那么甲出发多长时间后两人相遇
解:设甲出发x h后两人相遇.
根据题意,得60x+20(x+2)=200,解得x=2.
答:甲出发2h后两人相遇.
1.为增加展示作品的质感,需要准备一些相框进行展示,现
将一根木条进行切割制作相框,原计划制作正方形的相框,
现改为制作长方形的相框,若新的长方形相框的宽比原正方
形相框的边长少 ,新的长方形相框的长等于原正方形相
框的边长,且新的长方形相框需要用 长的木条,若设
原正方形相框的边长为 ,则可列方程为______________
_____.
2.为增加展示作品的美感,学校打算用彩纸包装相框.如图,
将一张正方形彩纸剪下一个宽为 的长条后,再从剩下的
长方形彩纸上剪去一个宽为 的长条.如果两次剪下的长
条面积相等,那么每一个长条的面积为_____ .
150
3.(8分)为增加展示现场的氛围感,学校决定购买彩色的地垫,
进行地面装饰.如图,其中一部分图案为用8个相同的小长方
形拼成的大长方形,求1个小长方形的面积.
解:设1个小长方形的宽为 ,根
据题图可知1个小长方形的长为
,则 ,解得
,则
答:1个小长方形的面积为 .
知识点2 行程问题
4.[2025年1月滁州期末]一艘轮船在, 两个码头之间航
行,顺水航行需,逆水航行需.已知水流速度为 ,
求轮船在静水中的航行速度.若设轮船在静水中的航行速度为
,则可列一元一次方程为( )
B
A. B.
C. D.
5.[2025年1月马鞍山期末]已知学校距离敬老院 .小
明和小刚两人从学校出发去敬老院送水果,小明带着水果先
走了,然后小刚才出发.若小明每分钟行 ,小刚
每分钟行,则小刚用___ 可以追上小明.
5
6.(8分)[2024·合肥模拟]小刚和小强从, 两地同时出发,
小刚骑自行车,小强步行,沿同一条路线相向匀速而行,出
发后两人相遇,相遇时小刚比小强多行进 ,相遇
后小刚到达 地.两人的行进速度分别是多少?
解:设小刚的行进速度为 ,
则相遇时小刚走了,小强走了 ,
由题意,得,解得 ,
则小强的行进速度为
答:小刚的行进速度是 ,小强的行进速度是
.
2星题 中档练
7.数学文化 我国古代名著《九章算术》中有一个问题,原文:
“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫
雁俱起,问何日相逢?”译文:野鸭从南海出发,7天后到达
北海;大雁从北海出发,9天后到达南海,今野鸭和大雁分
别从南海和北海同时出发,几天后相遇?设 天后相遇,可
列方程为( )
B
A. B.
C. D.
8.匀速行驶的动车经过一座大桥时,动车从车头上桥到车头
离桥共需要 ;而从动车车尾上桥开始到车头离桥结束,
整列动车完全在桥上的时间是 .已知该列动车长为
,则动车经过的这座大桥的长度为_______ .
9.(8分) 教材改编题 [2025· 安庆月考] 将一个底面内径是
,高是 的圆柱体桶内装满水,再将桶内的水倒
入一个底面内径是,高是 的圆柱体玻璃杯内,
能否完全装下?若装不下,则桶内还有多高的水?若没装满,
求杯内水面的高度.
解:不能完全装下.由题意得,水的体积为
.圆柱体玻璃杯的容积为
.因为 ,即水的体
积大于圆柱体玻璃杯的容积,所以不能完全装下.设桶内还有
高的水,由题意,得 ,解得
.故桶内还有 高的水.
10.(12分)真实情境如图是两张不同类型火车(“ 次”表
示动车,“ 次”表示高铁)的车票的部分信息.
(1)根据车票中的信息填空:该列动车和高铁是____
(填“相”或“同”)向而行,并且动车比高铁发车____
(填“早”或“晚”);
同
早
(2)已知该列动车和高铁的平均速度分别为 ,
,两列火车的长度不计,高铁比动车早到 ,求
, 两地之间的距离;
解:设,两地之间的距离为 .
根据题意得,解得 .
答:,两地之间的距离为 .
(3)在(2)的条件下,若
高铁到达 地后停止运
动,求高铁出发多少
小时后两车相距 .
设高铁出发后两车相距 ,
①当高铁还未追上动车时, ,解
得;②当高铁追上动车后, ,
解得;③当高铁到达 地,动车还未到达时,
,解得 .
答:高铁出发或 或
后两车相距 .
课堂小结
用一元一次方程解决实际问题的基本过程
实际问题
找等量关系,列方程
数学问题
(一元一次方程)
解方程
数学问题的解
(一元一次方程的解)
检验
实际问题的答案
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
