3.3.3比例、配套及工程问题 课件（共34张PPT）

(共34张PPT)
3.3.3比例、配套及工程问题
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师：********
班 级：********
时 间：********
3.3.3 比例、配套及工程问题
汇报人：[教师姓名]
汇报班级：[具体班级]
知识回顾
前面我们学习了储蓄问题和销售问题，它们都是生活中常见的实际问题。今天我们将继续学习另外三类重要的实际问题 —— 比例问题、配套问题和工程问题。这些问题在生产、生活中也经常出现，掌握用一元一次方程解决它们的方法，能让我们更好地应对实际生活中的数学问题。
学习目标
理解比例问题的含义，能根据比例的基本性质解决相关的实际问题。
掌握配套问题中各部分之间的数量关系，能运用一元一次方程解决配套问题。
明确工程问题中的工作总量、工作效率和工作时间的关系，会用一元一次方程解决工程问题。
进一步巩固列一元一次方程解应用题的步骤，提高分析和解决问题的能力。
知识点：比例问题
比例问题是指涉及到各部分数量之间比例关系的问题，解决这类问题的关键是根据比例设未知数，再结合总量等条件列出方程。
相关概念及数量关系
比例：表示两个或多个比相等的式子。例如，\(a:b = c:d\)。
比例的基本性质：在比例里，两个外项的积等于两个内项的积。即如果\(a:b = c:d\)，那么\(ad = bc\)。
若已知几个量的比例为\(m:n:p\)，则可设这几个量分别为\(mx\)、\(nx\)、\(px\)（\(x\)为常数），再根据总量等条件列方程。
例题解析
例 1：某班共有学生 56 人，男生与女生的人数比为 4:3，求该班男生和女生的人数。
解：审：已知班级总人数 56 人，男女生人数比 4:3，求男女生人数。
设：因为男生与女生的人数比为 4:3，所以设男生人数为\(4x\)人，女生人数为\(3x\)人。
找：等量关系是 “男生人数 + 女生人数 = 总人数”。
列：根据等量关系，列出方程：\(4x + 3x = 56\)。
解：解这个方程：\(
\begin{align*}
7x&=56\\
x&=8
\end{align*}
\)
则男生人数为\(4x = 4 8 = 32\)人，女生人数为\(3x = 3 8 = 24\)人。
验：男生 32 人，女生 24 人，总人数\(32 + 24 = 56\)人，人数比\(32:24 = 4:3\)，符合题意。
答：该班男生有 32 人，女生有 24 人。
例 2：甲、乙、丙三个数的和是 180，甲、乙、丙三个数的比是 2:3:4，求这三个数分别是多少。
解：审：已知三个数的和 180，比例 2:3:4，求这三个数。
设：设甲、乙、丙三个数分别为\(2x\)、\(3x\)、\(4x\)。
找：等量关系是 “甲 + 乙 + 丙 = 180”。
列：根据等量关系，列出方程：\(2x + 3x + 4x = 180\)。
解：解这个方程：\(
\begin{align*}
9x&=180\\
x&=20
\end{align*}
\)
则甲数为\(2x = 2 20 = 40\)，乙数为\(3x = 3 20 = 60\)，丙数为\(4x = 4 20 = 80\)。
验：\(40 + 60 + 80 = 180\)，比例\(40:60:80 = 2:3:4\)，符合题意。
答：甲、乙、丙三个数分别是 40、60、80。
例 3：某工厂有三个车间，第一车间与第二车间的人数比是 3:2，第二车间与第三车间的人数比是 4:5，已知三个车间的总人数是 150 人，求每个车间的人数。
解：审：已知一、二车间人数比 3:2，二、三车间人数比 4:5，总人数 150 人，求各车间人数。
分析：先统一比例，一、二车间人数比 3:2 = 6:4，所以一、二、三车间人数比为 6:4:5。
设：设第一、二、三车间的人数分别为\(6x\)、\(4x\)、\(5x\)。
找：等量关系是 “三个车间总人数 = 150 人”。
列：根据等量关系，列出方程：\(6x + 4x + 5x = 150\)。
解：解这个方程：\(
\begin{align*}
15x&=150\\
x&=10
\end{align*}
\)
则第一车间人数为\(6x = 6 10 = 60\)人，第二车间人数为\(4x = 4 10 = 40\)人，第三车间人数为\(5x = 5 10 = 50\)人。
验：总人数\(60 + 40 + 50 = 150\)人，一、二车间人数比\(60:40 = 3:2\)，二、三车间人数比\(40:50 = 4:5\)，符合题意。
答：第一车间有 60 人，第二车间有 40 人，第三车间有 50 人。
知识点：配套问题
配套问题是指在生产过程中，不同的零件或产品之间按照一定的比例进行搭配，以完成一个完整的产品，解决这类问题的关键是找出各部分之间的配套比例关系。
数量关系
根据配套要求，某一种零件的数量与另一种零件的数量成一定的比例，即两种零件的数量比等于配套比。例如，生产一个甲产品需要 2 个 A 零件和 3 个 B 零件，则 A 零件和 B 零件的数量比应为 2:3。
例题解析
例 4：某车间有 22 名工人，每人每天可以生产 1200 个螺钉或 2000 个螺母。1 个螺钉需要配 2 个螺母，为使每天生产的螺钉和螺母刚好配套，应安排多少名工人生产螺钉，多少名工人生产螺母？
解：审：有 22 名工人，每人每天产 1200 个螺钉或 2000 个螺母，1 螺钉配 2 螺母，求生产螺钉和螺母的工人数。
设：设应安排\(x\)名工人生产螺钉，则安排\((22 - x)\)名工人生产螺母。
分析：每天生产的螺钉数量为\(1200x\)个，每天生产的螺母数量为\(2000(22 - x)\)个，因为 1 个螺钉配 2 个螺母，所以螺母数量是螺钉数量的 2 倍。
找：等量关系是 “螺母数量 = 2× 螺钉数量”。
列：根据等量关系，列出方程：\(2000(22 - x)=2 1200x\)。
解：解这个方程：\(
\begin{align*}
44000 - 2000x&=2400x\\
44000&=4400x\\
x&=10
\end{align*}
\)
则生产螺母的工人数为\(22 - x = 22 - 10 = 12\)名。
验：10 名工人生产螺钉，每天产\(1200 10 = 12000\)个；12 名工人生产螺母，每天产\(2000 12 = 24000\)个，\(24000 = 2 12000\)，刚好配套，符合题意。
答：应安排 10 名工人生产螺钉，12 名工人生产螺母。
例 5：用白铁皮做罐头盒，每张铁皮可制盒身 25 个或制盒底 40 个，1 个盒身与 2 个盒底配成 1 个罐头盒。现有 36 张白铁皮，用多少张制盒身，多少张制盒底可以使盒身与盒底刚好配套？
解：审：有 36 张铁皮，每张制 25 个盒身或 40 个盒底，1 盒身配 2 盒底，求制盒身和盒底的铁皮张数。
设：设用\(x\)张铁皮制盒身，则用\((36 - x)\)张铁皮制盒底。
分析：可制盒身\(25x\)个，可制盒底\(40(36 - x)\)个，因为 1 个盒身配 2 个盒底，所以盒底数量是盒身数量的 2 倍。
找：等量关系是 “盒底数量 = 2× 盒身数量”。
列：根据等量关系，列出方程：\(40(36 - x)=2 25x\)。
解：解这个方程：\(
\begin{align*}
1440 - 40x&=50x\\
1440&=90x\\
x&=16
\end{align*}
\)
则制盒底的铁皮张数为\(36 - x = 36 - 16 = 20\)张。
验：16 张制盒身，可制\(25 16 = 400\)个；20 张制盒底，可制\(40 20 = 800\)个，\(800 = 2 400\)，刚好配套，符合题意。
答：用 16 张制盒身，20 张制盒底可以使盒身与盒底刚好配套。
知识点：工程问题
工程问题是指涉及到工作总量、工作效率和工作时间的问题，通常将工作总量看作单位 “1”。
相关概念及数量关系
工作总量：指总的工作量，通常设为单位 “1”。
工作效率：指单位时间内完成的工作量，工作效率 =\(\frac{ · é }{ · é }\)。
工作时间：指完成工作总量所需的时间。
基本数量关系：
工作总量 = 工作效率 × 工作时间
合作的工作效率 = 各部分工作效率之和
各部分工作量之和 = 工作总量
例题解析
例 6：一件工作，甲单独做需要 10 天完成，乙单独做需要 15 天完成。两人合作，需要几天完成？
解：审：甲独做 10 天完成，乙独做 15 天完成，求两人合作完成的时间。
设：设两人合作需要\(x\)天完成。
分析：把这件工作的总量看作单位 “1”，甲的工作效率是\(\frac{1}{10}\)，乙的工作效率是\(\frac{1}{15}\)，两人合作的工作效率是\(\frac{1}{10}+\frac{1}{15}\)。
找：等量关系是 “合作的工作效率 × 合作时间 = 工作总量”。
列：根据等量关系，列出方程：\((\frac{1}{10}+\frac{1}{15})x = 1\)。
解：解这个方程：\(
\begin{align*}
(\frac{3}{30}+\frac{2}{30})x&=1\\
\frac{5}{30}x&=1\\
\frac{1}{6}x&=1\\
x&=6
\end{align*}
\)
验：两人合作 6 天，甲完成\(\frac{1}{10} 6=\frac{3}{5}\)，乙完成\(\frac{1}{15} 6=\frac{2}{5}\)，总共完成\(\frac{3}{5}+\frac{2}{5}=1\)，符合题意。
答：两人合作需要 6 天完成。
例 7：一项工程，甲队单独做需要 12 天完成，乙队单独做需要 18 天完成。甲队先做 3 天，然后两队合作，还需要几天才能完成这项工程？
解：审：甲独做 12 天，乙独做 18 天，甲先做 3 天，再合作，求合作时间。
设：设两队合作还需要\(x\)天才能完成这项工程。
分析：工作总量为单位 “1”，甲的工作效率是\(\frac{1}{12}\)，乙的工作效率是\(\frac{1}{18}\)，甲先做 3 天完成的工作量是\(\frac{1}{12} 3\)，两队合作\(x\)天完成的工作量是\((\frac{1}{12}+\frac{1}{18})x\)。
找：等量关系是 “甲先做的工作量 + 两队合作的工作量 = 工作总量”。
列：根据等量关系，列出方程：\(\frac{1}{12} 3+(\frac{1}{12}+\frac{1}{18})x = 1\)。
解：解这个方程：\(
\begin{align*}
\frac{1}{4}+(\frac{3}{36}+\frac{2}{36})x&=1\\
\frac{1}{4}+\frac{5}{36}x&=1\\
\frac{5}{36}x&=\frac{3}{4}\\
x&=\frac{3}{4} \frac{36}{5}\\
x&=\frac{27}{5}=5.4
\end{align*}
\)
验：甲先做 3 天完成\(\frac{1}{4}\)，合作 5.4 天，甲完成\(\frac{1}{12} 5.4=\frac{9}{20}\)，乙完成\(\frac{1}{18} 5.4=\frac{3}{10}\)，总共完成\(\frac{1}{4}+\frac{9}{20}+\frac{3}{10}=1\)，符合题意。
答：还需要 5.4 天才能完成这项工程。
例 8：一个水池有甲、乙两个进水管和一个丙排水管，单独开甲管 6 小时可注满水池，单独开乙管 8 小时可注满水池，单独开丙管 12 小时可将满池水排空。若先打开甲、乙两管 2 小时，再打开丙管，问打开丙管后几小时可注满水池？
解：审：甲管 6 小时注满，乙管 8 小时注满，丙管 12 小时排空，先开甲、乙 2 小时，再开丙管，求注满水池还需的时间。
设：设打开丙管后\(x\)小时可注满水池。
分析：把水池的容积看作单位 “1”，甲管的注水效率是\(\frac{1}{6}\)，乙管的注水效率是\(\frac{1}{8}\)，丙管的排水效率是\(\frac{1}{12}\)。甲、乙两管先开 2 小时的注水量是\((\frac{1}{6}+\frac{1}{8}) 2\)，打开丙管后\(x\)小时的净注水量是\((\frac{1}{6}+\frac{1}{8}-\frac{1}{12})x\)。
找：等量关系是 “甲、乙先注的水量 + 打开丙管后净注水量 = 水池容积”。
列：根据等量关系，列出方程：\((\frac{1}{6}+\frac{1}{8}) 2+(\frac{1}{6}+\frac{1}{8}-\frac{1}{12})x = 1\)。
解：解这个方程：
[
\begin {align*}
(\frac {4}{24}+\frac {3}{24})×2+(\frac {4}{24}+\frac {3}{24}-\frac {2}{24}) x&=1\
\frac {7}{24}
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
复习回顾
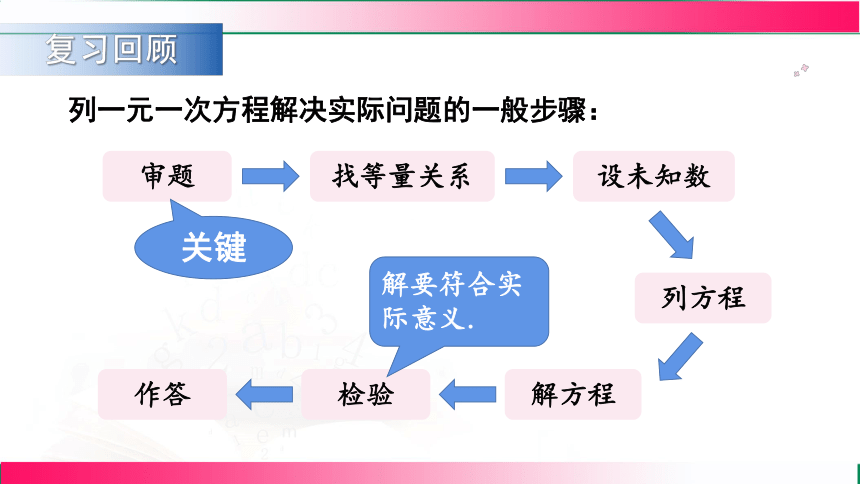
列一元一次方程解决实际问题的一般步骤：
审题
找等量关系
设未知数
列方程
解方程
检验
作答
关键
解要符合实际意义.
探索新知
例5：三支农机服务队共同为某镇抢收小麦300 hm2. 如果三支服务队收割小麦的面积之比为4∶5∶6，求他们分别收割小麦多少公顷.
【教材P106 例5】
分析：小麦面积共有4+5+6=15份，总计300 hm2.
怎样设未知数，说说你的想法.
探索新知
例5：三支农机服务队共同为某镇抢收小麦300 hm2. 如果三支服务队收割小麦的面积之比为4∶5∶6，求他们分别收割小麦多少公顷.
【教材P106 例5】
解：设收割小麦的面积每份为x hm2，三支服务队收割面积分别为4x hm2，5x hm2，6x hm2．
根据题意，得4x+5x+6x=300.
解方程，得x=20.
4x=80，5x=100，6x=120.
答：三支服务队分别收割小麦80 hm2，100 hm2，120 hm2.
间接设未知数法
比例应用题特征：设每一份为x较为方便.
某种中成药需要用到甘草、党参、 苏叶三种材料，其中甘草、党参、苏叶三种材料的质量之比 为1∶2∶4. 求生产210kg这种中成药，需要用到甘草、党参、 苏叶的质量分别是多少千克
练一练
解：设需要用到甘草、党参、苏叶的质量分别是x kg，2x kg，4x kg.
根据题意，得x+2x+4x=210.
解得x=30.
所以2x=60，4x=120.
答：需要用到甘草、党参、苏叶的质量分别是30kg，60kg，120kg.
随堂练习
1.为鼓励学生参加体育锻炼，学校计划购买一批篮球和排球.已知篮球和排球的单价之比为4∶3，单价之和为84元，则篮球的单价为_____元，排球的单价为_____元.
48
36
2.长方形的长与宽之比为5∶2，周长为56 cm，求这个长方形的面积.
【教材P106 练习 第1题】
解：设长方形的长为5x cm，则宽为2x cm.
根据题意，得2(5x+2x)=56.
解方程，得x=4.
5x=20，2x=8.
故长方形的面积为20×8=160(cm2).
3.兄弟两人合伙从事经营，哥哥入股250000元，弟弟入股200000元，一年后盈利83520元. 按入股的资金比例分配盈利，兄弟两人各应分得多少元
【教材P106 练习 第2题】
解：哥哥、弟弟入股的资金比例为250000∶ 200000= 5∶4. 设哥哥应分得盈利5x元，则弟弟应分得盈利4x元.
根据题意，得5x+4x=83520.
解方程，得x=9280.
5x=46400，4x=37120.
答：兄弟两人各应分得46400元和37120元.
4.今年元旦，小颖在如图所示的一张长方形宣纸上的四个正方形格子中写下了“元旦快乐”的毛笔书法作品，已知宣纸的长为108cm，正方形格子的边长相等，正方形格子与纸边之间的边空宽相等，相邻两个字的字距相等，且边空宽、字宽、字距之比为 3∶6∶2，则这张长方形宣纸的面积为_________cm2.
2个边空宽+4个字宽+3个字距=宣纸长
3888
1星题 基础练
知识点1 比例问题
1.一条绳子长，需按 的比例截成4段，求每段
绳子长多少米.若设每份长为 ，则第一段绳子的长为
，其余三段绳子的长分别为___________________，可
列方程为________________________.
，，
2.教材改编题 有某种三色冰激凌 ，咖啡色、红色和白色
配料的比是 ，这种三色冰激凌中咖啡色配料有( )
A
A. B. C. D.
3.甲、乙、丙三人共同出资做生意，甲投资了24万元，乙投资
了20万元，丙投资了28万元，年终时，共赚得利润27万元，甲、
乙、丙三人按出资比例进行分配，甲可以分得利润___万元.
9
知识点2 配套问题
主题情境
某中学七年级在操场上举办了趣味运动会，1班和2班负责投
壶游戏里的道具和奖品，请完成题.
4.已知1个投壶和6支羽箭配成一套道具，其中一个投壶15元，
一支羽箭3元，两个班在投壶道具上的经费是132元，请问如
何分配经费使购买的道具刚好配套呢？设 元购买投壶，则
所列方程正确的是( )
C
A. B.
C. D.
5.从两个班中选出28名学生制作长方体礼盒，用来装奖品，
每人每小时可做6个侧面或9个底面，一个礼盒由1个侧面和2
个底面组成，为了使每小时制作的成品刚好配套，应该分配
____名学生做侧面，____名学生做底面.
12
16
知识点3 工程问题
6.某工程甲队单独完成要25天，乙队单独完成要20天.若乙队
先单独干10天，剩下的由甲队单独完成，设一共用 天完成，
则可列方程为( )
B
A. B.
C. D.
7.［2025·合肥月考］某工程队修一条公路，第一天修了全程
的，第二天修了余下的，还剩下 没修，则这条
公路长_______ .
8.(8分) 真实情境 [2025年1月连云港期末] 某工厂承接一批
太阳能电池板生产任务，请你根据甲、乙两名工人的对话内
容(如图)，解决下列问题.
(1)问甲、乙两名工人单独加工完这批零件，各需要多少天？
解：设甲单独加工完这批零件需要 天，则乙单独加工完这
批零件需要 天，由题意得
，解得，所以 .
答：甲单独加工完这批零件需要15天，乙单独加工完这批零
件需要10天.
(2)这批零件先由乙单独加工5天，剩下的部分由甲、乙合作
完成，那么加工完这批零件，甲、乙各获得多少报酬？
设剩下的部分由甲、乙合作 天完成，
由题意得，解得 .
(元)， (元).
答：加工完这批零件，甲获得480元的报酬，乙获得1 920元
的报酬.
2星题 中档练
9.［2025年1月淮北期末］20名学生在进行一次科学实践活动
时，需要组装一种实验仪器，该仪器每套是由3个 部件和2
个部件组成的.在规定时间内，每人可以组装好10个 部件
或20个 部件.那么在规定时间内，最多可以组装出____套这
种实验仪器.
50
10.甲、乙两个工程队完成一项工程，每天完成的工作量始终
保持不变.甲队先干了3天，然后乙队加入，合作完成剩下的
工程，设工作总量为1.下面是未记录完整的工程进度表.根据
表中的数据，可知的值为__， 的值为___.
天数 第1天 第2天 第3天 第4天 第5天 …
工程总进度 … 1
9
11.(8分)为提高销售业绩，安徽省某茶叶专卖店店长对店内
销售额居于前三的六安瓜片、黄山毛峰、太平猴魁三种茶叶
的销售额进行了分析，发现上月三种茶叶销售额的比值为
，六安瓜片本月的销售额是上月销售额的 倍，黄山毛
峰本月的销售额是上月销售额的 倍，太平猴魁本月的
销售额与上月的相同，同时这三种茶叶本月的总销售额恰好
是上月总销售额的2倍，求六安瓜片本月的销售额与上月销
售额的比值.
解：由题意，可设上月六安瓜片、黄山毛峰、太平猴魁三种
茶叶的销售额分别为元，元， 元，则
，解得 ，
即六安瓜片本月的销售额与上月销售额的比值为 .
12.(8分)创新题·新设问 [2024·合肥期末] 为建设文明城市，
某社区计划将社区内一条东西走向的水泥道路铺设成柏油路，
俗称“白改黑”.甲工程队负责这条道路的铺设，他们从西头开
始铺，计划6天内完成.第一天铺了全长的 ，第二天铺的比
第一天的2倍少，此时还剩下全长的 没铺.
(1)若用线段图1表示前两天甲工程队的进度情况，请写出图1
中①处应填写的内容，并写出图1中 所表示的实际意义，再
求出它的值；
解：①处应填写， 表示这条道路的全长.
根据题意，得 ，解得
.
(2)为按时完成铺路任务，从第三天开始，甲工程队加快速度，
同时乙工程队加入铺路，从东头开始铺.两队的进展情况如线
段图2所示，请根据线段图提出一个问题并进行解答.
(答案不唯一)提出的问题：加速后，甲工程队每天铺多少米？
甲工程队前两天共铺路
.
根据题意，得 ，
解得 .
答：加速后，甲工程队每天铺 .
课堂小结
在比例问题中，合理设未知数是解题的关键，常利用参数法间接设未知数. 如：若甲、乙的配比为m∶n，常常设“每一份”为x，即设甲为mx，则乙可表示为nx，然后根据等量关系建立方程模型.
谢谢观看！