3.4.1二元一次方程组 课件(共37张PPT)
文档属性
| 名称 | 3.4.1二元一次方程组 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览











文档简介
(共37张PPT)
3.4.1二元一次方程组
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
3.4.1 二元一次方程组
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
在前面的学习中,我们已经掌握了一元一次方程的相关知识,知道只含有一个未知数(元),未知数的次数都是 1,等号两边都是整式的方程叫做一元一次方程。今天我们将学习一种新的方程类型 —— 二元一次方程,以及由多个二元一次方程组成的二元一次方程组。
学习目标
理解二元一次方程、二元一次方程组的概念,能识别二元一次方程和二元一次方程组。
知道二元一次方程的解和二元一次方程组的解的含义,能检验一组数是不是二元一次方程(组)的解。
经历从实际问题中抽象出二元一次方程组的过程,体会方程是刻画现实世界数量关系的有效模型。
培养观察、分析和概括的能力,感受数学与生活的联系。
课堂导入
我们来看一个生活中的问题:小明去商店买笔和笔记本,已知买 1 支笔和 1 本笔记本一共花了 8 元,买 2 支笔和 3 本笔记本一共花了 21 元,那么 1 支笔和 1 本笔记本分别多少钱?
如果我们设 1 支笔的价格为\(x\)元,1 本笔记本的价格为\(y\)元,根据题意可以列出两个方程:\(x + y = 8\)和\(2x + 3y = 21\)。这两个方程中都含有两个未知数,且未知数的次数都是 1,像这样的方程就是二元一次方程,而这两个方程合在一起就组成了一个二元一次方程组。通过解这个方程组,我们就能求出笔和笔记本的单价。这就是我们本节课要学习的内容。
知识点:二元一次方程
定义
含有两个未知数,并且含有未知数的项的次数都是 1 的整式方程,叫做二元一次方程。
例如:\(x + y = 5\)、\(2a - 3b = 7\)都是二元一次方程。
注意事项
方程中必须含有两个未知数;
含有未知数的项的次数都是 1,而不是未知数的次数是 1。例如,方程\(xy = 6\)中,含有未知数的项\(xy\)的次数是 2,所以它不是二元一次方程;
方程的两边必须都是整式。
二元一次方程的解
使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
例如,对于方程\(x + y = 5\),当\(x = 2\),\(y = 3\)时,方程左边\(=2 + 3=5\),右边\(=5\),左边 = 右边,所以\(\begin{cases}x = 2\\y = 3\end{cases}\)是方程\(x + y = 5\)的解。
二元一次方程的解有无数个,只要给定其中一个未知数的值,就可以求出另一个未知数的值。
例题解析
例 1:判断下列方程是不是二元一次方程:
(1)\(3x + y = 4\);
(2)\(2x + 3 = 7\);
(3)\(xy + 1 = 0\);
(4)\(x + \frac{1}{y}=2\)。
解:(1)方程\(3x + y = 4\)含有两个未知数\(x\)和\(y\),含有未知数的项的次数都是 1,且两边都是整式,所以是二元一次方程。
(2)方程\(2x + 3 = 7\)只含有一个未知数\(x\),所以不是二元一次方程。
(3)方程\(xy + 1 = 0\)中,含有未知数的项\(xy\)的次数是 2,所以不是二元一次方程。
(4)方程\(x + \frac{1}{y}=2\)中,\(\frac{1}{y}\)不是整式,所以不是二元一次方程。
例 2:已知\(\begin{cases}x = 1\\y = -2\end{cases}\)是方程\(2x + my = 7\)的解,求\(m\)的值。
解:因为\(\begin{cases}x = 1\\y = -2\end{cases}\)是方程\(2x + my = 7\)的解,所以将\(x = 1\),\(y = -2\)代入方程中,等式成立,即:\(2 1 + m (-2)=7\)
化简得:\(2 - 2m = 7\)
移项得:\(-2m = 7 - 2\)\(-2m = 5\)
系数化为 1 得:\(m=-\frac{5}{2}\)
知识点:二元一次方程组
定义
由几个含有相同未知数的二元一次方程合在一起,就组成了一个二元一次方程组。
例如:\(\begin{cases}x + y = 8\\2x + 3y = 21\end{cases}\)、\(\begin{cases}3a - b = 5\\a + 2b = 4\end{cases}\)都是二元一次方程组。
注意事项
方程组中含有两个未知数;
方程组中的每个方程都是二元一次方程;
“合在一起” 通常是指用大括号 “\(\begin{cases}\end{cases}\)” 把它们连接起来。
二元一次方程组的解
二元一次方程组中的两个方程的公共解,叫做二元一次方程组的解。
例如,方程组\(\begin{cases}x + y = 8\\2x + 3y = 21\end{cases}\),我们可以通过尝试找到它的解。当\(x = 3\),\(y = 5\)时,第一个方程左边\(=3 + 5 = 8\),右边\(=8\);第二个方程左边\(=2 3 + 3 5=6 + 15 = 21\),右边\(=21\),所以\(\begin{cases}x = 3\\y = 5\end{cases}\)是这个方程组的解。
例题解析
例 3:判断下列方程组是不是二元一次方程组:
(1)\(\begin{cases}x + y = 3\\x - y = 1\end{cases}\);
(2)\(\begin{cases}x + 2y = 5\\3z - y = 4\end{cases}\);
(3)\(\begin{cases}x^2 + y = 7\\x - y = 2\end{cases}\);
(4)\(\begin{cases}x + y = 6\\\frac{1}{x} + y = 2\end{cases}\)。
解:(1)方程组\(\begin{cases}x + y = 3\\x - y = 1\end{cases}\)含有两个未知数\(x\)和\(y\),每个方程都是二元一次方程,所以是二元一次方程组。
(2)方程组\(\begin{cases}x + 2y = 5\\3z - y = 4\end{cases}\)含有三个未知数\(x\)、\(y\)、\(z\),所以不是二元一次方程组。
(3)方程组\(\begin{cases}x^2 + y = 7\\x - y = 2\end{cases}\)中,第一个方程含有未知数的项\(x^2\)的次数是 2,不是二元一次方程,所以不是二元一次方程组。
(4)方程组\(\begin{cases}x + y = 6\\\frac{1}{x} + y = 2\end{cases}\)中,第二个方程含有\(\frac{1}{x}\),不是整式方程,所以不是二元一次方程组。
例 4:检验\(\begin{cases}x = 2\\y = 1\end{cases}\)和\(\begin{cases}x = 1\\y = -1\end{cases}\)是不是方程组\(\begin{cases}2x + y = 5\\x - y = 1\end{cases}\)的解。
解:将\(\begin{cases}x = 2\\y = 1\end{cases}\)代入方程组:
第一个方程:左边\(=2 2 + 1 = 5\),右边\(=5\),左边 = 右边;
第二个方程:左边\(=2 - 1 = 1\),右边\(=1\),左边 = 右边。
所以\(\begin{cases}x = 2\\y = 1\end{cases}\)是方程组的解。
将\(\begin{cases}x = 1\\y = -1\end{cases}\)代入方程组:
第一个方程:左边\(=2 1 + (-1)=1\),右边\(=5\),左边≠右边;
所以\(\begin{cases}x = 1\\y = -1\end{cases}\)不是方程组的解。
小练习
下列方程中,是二元一次方程的是( )
A. \(x + y^2 = 0\) B. \(x = \frac{2}{y} + 1\) C. \(x - 2y = 3\) D. \(xy = 6\)
若\(\begin{cases}x = 3\\y = -1\end{cases}\)是方程\(3x + my = 6\)的解,则\(m = \)
下列方程组中,是二元一次方程组的是( )
A. \(\begin{cases}x + y = 5\\x^2 = 3\end{cases}\) B. \(\begin{cases}x + y = 2\\y + z = 3\end{cases}\) C. \(\begin{cases}x - y = 1\\2x + 3y = 10\end{cases}\) D. \(\begin{cases}\frac{1}{x} + y = 3\\x - y = 4\end{cases}\)
写出二元一次方程\(x + 2y = 5\)的三个解。
检验\(\begin{cases}x = 3\\y = 2\end{cases}\)是不是方程组\(\begin{cases}x + y = 5\\2x - y = 4\end{cases}\)的解。
思考讨论
二元一次方程和一元一次方程有什么区别和联系?
区别:二元一次方程含有两个未知数,而一元一次方程含有一个未知数;二元一次方程有无数个解,而一元一次方程只有一个解。
联系:它们都是整式方程,且未知数的最高次数都是 1;在解二元一次方程组时,常常会通过消元的方法将其转化为一元一次方程来求解。
如何理解二元一次方程组的解的含义?
二元一次方程组的解是方程组中所有方程的公共解,即它既要满足方程组中的第一个方程,又要满足方程组中的第二个方程。也就是说,将这组解代入方程组中的每个方程,等式都成立。
课堂小结
二元一次方程:含有两个未知数,并且含有未知数的项的次数都是 1 的整式方程。其解是使方程两边的值相等的两个未知数的值,有无数个解。
二元一次方程组:由几个含有相同未知数的二元一次方程合在一起组成的方程组。其解是方程组中两个方程的公共解,通常只有一个解(特殊情况下可能无解或有无数个解)。
判断一个方程是不是二元一次方程,要紧扣定义,看是否满足 “含有两个未知数、含有未知数的项的次数都是 1、整式方程” 这三个条件;判断一个方程组是不是二元一次方程组,要看是否含有两个未知数且每个方程都是二元一次方程。
检验一组数是不是二元一次方程组的解,只需将这组数代入方程组中的每个方程,若所有方程都成立,则是方程组的解,否则不是。
课后作业
下列方程中,哪些是二元一次方程?
(1)\(3x - y = 0\);(2)\(x + \frac{1}{y} = 2\);(3)\(x^2 + y = 5\);(4)\(2x + 3y = z\)。
若\(\begin{cases}x = -1\\y = 2\end{cases}\)是方程\(2x + ay = 4\)的解,求\(a\)的值。
下列方程组中,哪些是二元一次方程组?
(1)\(\begin{cases}x + y = 3\\2x - y = 1\end{cases}\);(2)\(\begin{cases}x + y = 5\\xy = 6\end{cases}\);(3)\(\begin{cases}x = 1\\y = 2\end{cases}\);(4)\(\begin{cases}\frac{x}{2} + \frac{y}{3} = 1\\x - y = 2\end{cases}\)。
写出二元一次方程\(3x - 2y = 6\)的两个解。
检验\(\begin{cases}x = 4\\y = 3\end{cases}\)是不是方程组\(\begin{cases}x + y = 7\\x - y = 1\end{cases}\)的解。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
复习回顾
只含有_______未知数(元),未知数的次数都是____,且等式两边都是_______的方程叫作一元一次方程.
下列式子中,是一元一次方程的是_______(填序号).
① x-2= ;② 0.3x=1;③ =5x+1;④ x2-4x=3;
⑤ x=6;⑥ x+2y=0.
一个
1
整式
②③⑤
探索新知
问题1:“鸡兔同笼”是我国古代数学著作《孙子算经》上的一道题. 今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.
思考1:如何列一元一次方程?
解:设鸡有x只,则兔有(35-x)只.
2x+4(35-x)=94
思考2:问题中有两个未知数,能不能根据题意直接设两个未知数,使列方程变得容易呢?
分析:
鸡的只数+兔的只数=总头数
鸡的脚数+兔的脚数=总脚数
解:设鸡有x只,兔有y只.
鸡 兔 合计
头数 x y 35
脚数 2x 4y 94
x+y=35
2x+4y=94
x+y=35
2x+4y=94
观察下面的方程:
2.它与你学过的一元一次方程比较有什么区别?
1.它们有什么共同特征?
3.你能给它起个名字吗?
定义:含有两个未知数的一次方程叫作二元一次方程.
注意:
1.是整式方程;
2.只含有两个未知数,且未知数的系数不为0;
3. “一次”是指含未知数的项的次数是1,而不是未知数的次数.
x+y=35
2x+4y=94
二元一次方程
三者缺一不可!
下列式子中,是二元一次方程的是_______(填序号).
① 8x-y=3y;② 3x-z=y;③ 2x-5=3;④ +y=2;
⑤ xy=2;⑥ 3x2+1=y;⑦ x-y= .
练一练
判断一个方程是否为二元一次方程的方法:
1.原方程是否是整式方程且只含有两个未知数;
2.整理化简后的方程中两个未知数的系数都不为0,且含未知数的项的次数都是1.
①⑦
x+y=35
2x+4y=94
①
②
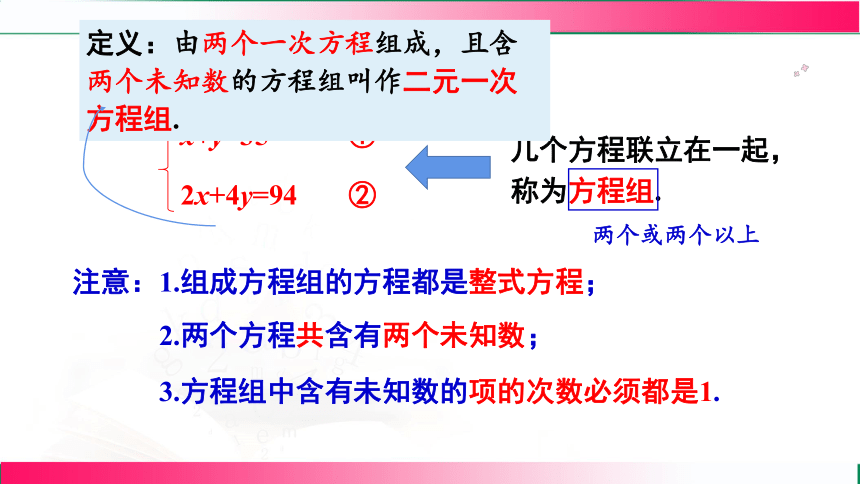
几个方程联立在一起,称为方程组.
两个或两个以上
定义:由两个一次方程组成,且含两个未知数的方程组叫作二元一次方程组.
注意:
1.组成方程组的方程都是整式方程;
2.两个方程共含有两个未知数;
3.方程组中含有未知数的项的次数必须都是1.
下列方程组中,是二元一次方程组的是( )
练一练
A. B. C. D.
看两个方程是否为整式方程
看方程组是否一共含有两个未知数
看含未知数的项的次数是否都是1
C
问题2:某班同学在植树节时植樟树和白杨树共50棵. 已知樟树苗每棵10元,白杨树苗每棵3元,购买这些树苗用了290元.樟树苗、白杨树苗各买了多少棵
设樟树苗买了x棵,白杨树苗买了y棵,可得二元一次方程组
x+y=50,
10x+3y=290.
①
②
随堂练习
1.已知2xa-5-(b-2)y|b|-1=4是关于x,y的二元一次方程,则
a-2b=________.
10
2.若 是关于x,y的二元一次方程组,则
a=________,b=________.
﹣1
5
3.根据题意,列出二元一次方程组:
(1)小华买了60分与80分的邮票共10枚,花了7元2角,那么60分和80分的邮票各买了多少枚
【教材P109 练习 第1题】
解:设买了x枚60分的邮票和y枚80分的邮票.
根据题意,得
(2)植树节七(1)班和七(2)班共植树138棵,七(1)班植树数量比七(2)班的 多8棵. 两班分别植树多少棵
解:设七(1)班植树x棵,七(2)班植树y棵.
根据题意,得
(3)将一摞笔记本分给若干同学. 每个同学5本,则剩下8本;每个同学8本,又差了7本. 共有多少本笔记本、多少个同学
解:设共有x本笔记本,y个同学.
根据题意,得
4.请你根据生活实例,编一道应用二元一次方程组的问题,并列出方程组.
解:答案不唯一,如:某船的载重为260t,容积为1000m3. 现有甲、乙两种货物要运,其中甲种货物每吨体积为8m3,乙种货物每吨体积为2m3,若要充分利用这艘船的载重与容积,则甲、乙两种货物应各装多少吨(装运货物时不留空隙)?
设甲、乙两种货物应各装x t,y t.
根据题意,得
【教材P109 练习 第2题】
1星题 基础练
知识点1 二元一次方程
1.[2025·杭州月考]下列方程是二元一次方程的是( )
C
A. B.
C. D.
2.关于,的方程是二元一次方程,则
的取值范围是( )
C
A. B. C. D.
3.若方程是关于, 的二元一次方程,则
___.
3
知识点2 二元一次方程组
4.下列方程组是二元一次方程组的是( )
C
A. B.
C. D.
5.创新题·新考法 若方程组 是二元一次方程组,
则“……”不可能是( )
C
A. B. C. D.
6.[2025年1月安庆期末]若是关于,
的二元一次方程组,则___, ____.
1
知识点3 建立二元一次方程组模型
7.某班35名学生共种87棵树苗.其中男生每人种3棵,女生每
人种2棵,设该班男生有人,女生有 人.根据题意,所列方
程组正确的是( )
D
A. B.
C. D.
8.(8分)教材改编题 根据题意列二元一次方程组.
(1)一个长方形的周长是,宽比长短 ,求这个长方
形的长和宽.
解:设这个长方形的长为,宽为 ,则
(2)某校有两种类型的学生宿舍共30间,大宿舍每间可住8人,
小宿舍每间可住5人,该校住宿生198人恰好住满这30间宿舍,
大、小宿舍各有多少间?
设大宿舍有间,小宿舍有间,则
2星题 中档练
9.易错题 [2024·合肥庐阳区期末] 若方程
是关于,的二元一次方程,则 的值
为( )
D
A. B. C.0 D.1
10.已知方程组:
下列说法正确的是( )
D
A.只有①是二元一次方程组
B.只有②是二元一次方程组
C.只有②③是二元一次方程组
D.只有②不是二元一次方程组
11.数学文化 [2025年1月阜阳期
末] 《九章算术》中的“方程”
一章中讲述了算筹图,如图①②
所示,图中各行从左到右列出的算筹数分别表示未知数,
的系数与相应的常数项,图①表示的算筹图用我们现在所熟
悉的方程组形式表述出来为 类似地,图②所
示的算筹图用方程组可表述为
_ ______________.
12.若 ,则可转化为方程组:
_ ________________.
13.创新题·新考法 问题:“小明家离学校 ,其中有一
段为上坡路,另一段为下坡路.他跑步去学校共用时 ,
已知小明上坡的平均速度为 ,下坡的平均速度为
,小明上坡和下坡各用了多长时间?”
小亮设出未知数,后列出了方程组
则“……”表示的方程是___________,小颖设出未知数,
后却列了和小亮不同的方程组: 则“……”
表示的方程是___________________________.
14.(8分)[2025年1月芜湖期末]如图是
由截面为同一种长方形的墙砖组成的部
分墙面,其中3块横放的墙砖比1块竖放
的墙砖高,2块横放的墙砖比2块竖放的墙砖低 ,
试求每块墙砖截面的长和宽.若设每块墙砖的截面的长为
,宽为 ,请根据题意,列出二元一次方程组.
解:由“3块横放的墙砖比1块竖放的墙砖
高”得 .由“2块横放的墙
砖比2块竖放的墙砖低 ”得
.故可列出二元一次方程组
为
3星题 提升练
15.跨学科·语文 成语“朝三暮四”讲述了一位老翁喂养猴子的故事,老翁为
了限定猴子的食量分早晚两次投喂,早上的粮食是晚上的 ,猴子们对于
这个安排很不满意,于是老翁进行调整,从晚上的粮食中取2千克放在早
上投喂,这样早上的粮食是晚上的 ,猴子们对这样的安排非常满意.设调
整前早上的粮食是千克,晚上的粮食是 千克,则可列方程组为( )
A. B. C. D.
B
课堂小结
二元一次方程组
二元一次方程及二元一次方程组的定义
根据实际问题列二元一次方程组
含有两个未知数的一次方程叫作二元一次方程.
由两个一次方程组成,且含两个未知数的方程组叫作二元一次方程组.
谢谢观看!
3.4.1二元一次方程组
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
3.4.1 二元一次方程组
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
在前面的学习中,我们已经掌握了一元一次方程的相关知识,知道只含有一个未知数(元),未知数的次数都是 1,等号两边都是整式的方程叫做一元一次方程。今天我们将学习一种新的方程类型 —— 二元一次方程,以及由多个二元一次方程组成的二元一次方程组。
学习目标
理解二元一次方程、二元一次方程组的概念,能识别二元一次方程和二元一次方程组。
知道二元一次方程的解和二元一次方程组的解的含义,能检验一组数是不是二元一次方程(组)的解。
经历从实际问题中抽象出二元一次方程组的过程,体会方程是刻画现实世界数量关系的有效模型。
培养观察、分析和概括的能力,感受数学与生活的联系。
课堂导入
我们来看一个生活中的问题:小明去商店买笔和笔记本,已知买 1 支笔和 1 本笔记本一共花了 8 元,买 2 支笔和 3 本笔记本一共花了 21 元,那么 1 支笔和 1 本笔记本分别多少钱?
如果我们设 1 支笔的价格为\(x\)元,1 本笔记本的价格为\(y\)元,根据题意可以列出两个方程:\(x + y = 8\)和\(2x + 3y = 21\)。这两个方程中都含有两个未知数,且未知数的次数都是 1,像这样的方程就是二元一次方程,而这两个方程合在一起就组成了一个二元一次方程组。通过解这个方程组,我们就能求出笔和笔记本的单价。这就是我们本节课要学习的内容。
知识点:二元一次方程
定义
含有两个未知数,并且含有未知数的项的次数都是 1 的整式方程,叫做二元一次方程。
例如:\(x + y = 5\)、\(2a - 3b = 7\)都是二元一次方程。
注意事项
方程中必须含有两个未知数;
含有未知数的项的次数都是 1,而不是未知数的次数是 1。例如,方程\(xy = 6\)中,含有未知数的项\(xy\)的次数是 2,所以它不是二元一次方程;
方程的两边必须都是整式。
二元一次方程的解
使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解。
例如,对于方程\(x + y = 5\),当\(x = 2\),\(y = 3\)时,方程左边\(=2 + 3=5\),右边\(=5\),左边 = 右边,所以\(\begin{cases}x = 2\\y = 3\end{cases}\)是方程\(x + y = 5\)的解。
二元一次方程的解有无数个,只要给定其中一个未知数的值,就可以求出另一个未知数的值。
例题解析
例 1:判断下列方程是不是二元一次方程:
(1)\(3x + y = 4\);
(2)\(2x + 3 = 7\);
(3)\(xy + 1 = 0\);
(4)\(x + \frac{1}{y}=2\)。
解:(1)方程\(3x + y = 4\)含有两个未知数\(x\)和\(y\),含有未知数的项的次数都是 1,且两边都是整式,所以是二元一次方程。
(2)方程\(2x + 3 = 7\)只含有一个未知数\(x\),所以不是二元一次方程。
(3)方程\(xy + 1 = 0\)中,含有未知数的项\(xy\)的次数是 2,所以不是二元一次方程。
(4)方程\(x + \frac{1}{y}=2\)中,\(\frac{1}{y}\)不是整式,所以不是二元一次方程。
例 2:已知\(\begin{cases}x = 1\\y = -2\end{cases}\)是方程\(2x + my = 7\)的解,求\(m\)的值。
解:因为\(\begin{cases}x = 1\\y = -2\end{cases}\)是方程\(2x + my = 7\)的解,所以将\(x = 1\),\(y = -2\)代入方程中,等式成立,即:\(2 1 + m (-2)=7\)
化简得:\(2 - 2m = 7\)
移项得:\(-2m = 7 - 2\)\(-2m = 5\)
系数化为 1 得:\(m=-\frac{5}{2}\)
知识点:二元一次方程组
定义
由几个含有相同未知数的二元一次方程合在一起,就组成了一个二元一次方程组。
例如:\(\begin{cases}x + y = 8\\2x + 3y = 21\end{cases}\)、\(\begin{cases}3a - b = 5\\a + 2b = 4\end{cases}\)都是二元一次方程组。
注意事项
方程组中含有两个未知数;
方程组中的每个方程都是二元一次方程;
“合在一起” 通常是指用大括号 “\(\begin{cases}\end{cases}\)” 把它们连接起来。
二元一次方程组的解
二元一次方程组中的两个方程的公共解,叫做二元一次方程组的解。
例如,方程组\(\begin{cases}x + y = 8\\2x + 3y = 21\end{cases}\),我们可以通过尝试找到它的解。当\(x = 3\),\(y = 5\)时,第一个方程左边\(=3 + 5 = 8\),右边\(=8\);第二个方程左边\(=2 3 + 3 5=6 + 15 = 21\),右边\(=21\),所以\(\begin{cases}x = 3\\y = 5\end{cases}\)是这个方程组的解。
例题解析
例 3:判断下列方程组是不是二元一次方程组:
(1)\(\begin{cases}x + y = 3\\x - y = 1\end{cases}\);
(2)\(\begin{cases}x + 2y = 5\\3z - y = 4\end{cases}\);
(3)\(\begin{cases}x^2 + y = 7\\x - y = 2\end{cases}\);
(4)\(\begin{cases}x + y = 6\\\frac{1}{x} + y = 2\end{cases}\)。
解:(1)方程组\(\begin{cases}x + y = 3\\x - y = 1\end{cases}\)含有两个未知数\(x\)和\(y\),每个方程都是二元一次方程,所以是二元一次方程组。
(2)方程组\(\begin{cases}x + 2y = 5\\3z - y = 4\end{cases}\)含有三个未知数\(x\)、\(y\)、\(z\),所以不是二元一次方程组。
(3)方程组\(\begin{cases}x^2 + y = 7\\x - y = 2\end{cases}\)中,第一个方程含有未知数的项\(x^2\)的次数是 2,不是二元一次方程,所以不是二元一次方程组。
(4)方程组\(\begin{cases}x + y = 6\\\frac{1}{x} + y = 2\end{cases}\)中,第二个方程含有\(\frac{1}{x}\),不是整式方程,所以不是二元一次方程组。
例 4:检验\(\begin{cases}x = 2\\y = 1\end{cases}\)和\(\begin{cases}x = 1\\y = -1\end{cases}\)是不是方程组\(\begin{cases}2x + y = 5\\x - y = 1\end{cases}\)的解。
解:将\(\begin{cases}x = 2\\y = 1\end{cases}\)代入方程组:
第一个方程:左边\(=2 2 + 1 = 5\),右边\(=5\),左边 = 右边;
第二个方程:左边\(=2 - 1 = 1\),右边\(=1\),左边 = 右边。
所以\(\begin{cases}x = 2\\y = 1\end{cases}\)是方程组的解。
将\(\begin{cases}x = 1\\y = -1\end{cases}\)代入方程组:
第一个方程:左边\(=2 1 + (-1)=1\),右边\(=5\),左边≠右边;
所以\(\begin{cases}x = 1\\y = -1\end{cases}\)不是方程组的解。
小练习
下列方程中,是二元一次方程的是( )
A. \(x + y^2 = 0\) B. \(x = \frac{2}{y} + 1\) C. \(x - 2y = 3\) D. \(xy = 6\)
若\(\begin{cases}x = 3\\y = -1\end{cases}\)是方程\(3x + my = 6\)的解,则\(m = \)
下列方程组中,是二元一次方程组的是( )
A. \(\begin{cases}x + y = 5\\x^2 = 3\end{cases}\) B. \(\begin{cases}x + y = 2\\y + z = 3\end{cases}\) C. \(\begin{cases}x - y = 1\\2x + 3y = 10\end{cases}\) D. \(\begin{cases}\frac{1}{x} + y = 3\\x - y = 4\end{cases}\)
写出二元一次方程\(x + 2y = 5\)的三个解。
检验\(\begin{cases}x = 3\\y = 2\end{cases}\)是不是方程组\(\begin{cases}x + y = 5\\2x - y = 4\end{cases}\)的解。
思考讨论
二元一次方程和一元一次方程有什么区别和联系?
区别:二元一次方程含有两个未知数,而一元一次方程含有一个未知数;二元一次方程有无数个解,而一元一次方程只有一个解。
联系:它们都是整式方程,且未知数的最高次数都是 1;在解二元一次方程组时,常常会通过消元的方法将其转化为一元一次方程来求解。
如何理解二元一次方程组的解的含义?
二元一次方程组的解是方程组中所有方程的公共解,即它既要满足方程组中的第一个方程,又要满足方程组中的第二个方程。也就是说,将这组解代入方程组中的每个方程,等式都成立。
课堂小结
二元一次方程:含有两个未知数,并且含有未知数的项的次数都是 1 的整式方程。其解是使方程两边的值相等的两个未知数的值,有无数个解。
二元一次方程组:由几个含有相同未知数的二元一次方程合在一起组成的方程组。其解是方程组中两个方程的公共解,通常只有一个解(特殊情况下可能无解或有无数个解)。
判断一个方程是不是二元一次方程,要紧扣定义,看是否满足 “含有两个未知数、含有未知数的项的次数都是 1、整式方程” 这三个条件;判断一个方程组是不是二元一次方程组,要看是否含有两个未知数且每个方程都是二元一次方程。
检验一组数是不是二元一次方程组的解,只需将这组数代入方程组中的每个方程,若所有方程都成立,则是方程组的解,否则不是。
课后作业
下列方程中,哪些是二元一次方程?
(1)\(3x - y = 0\);(2)\(x + \frac{1}{y} = 2\);(3)\(x^2 + y = 5\);(4)\(2x + 3y = z\)。
若\(\begin{cases}x = -1\\y = 2\end{cases}\)是方程\(2x + ay = 4\)的解,求\(a\)的值。
下列方程组中,哪些是二元一次方程组?
(1)\(\begin{cases}x + y = 3\\2x - y = 1\end{cases}\);(2)\(\begin{cases}x + y = 5\\xy = 6\end{cases}\);(3)\(\begin{cases}x = 1\\y = 2\end{cases}\);(4)\(\begin{cases}\frac{x}{2} + \frac{y}{3} = 1\\x - y = 2\end{cases}\)。
写出二元一次方程\(3x - 2y = 6\)的两个解。
检验\(\begin{cases}x = 4\\y = 3\end{cases}\)是不是方程组\(\begin{cases}x + y = 7\\x - y = 1\end{cases}\)的解。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
复习回顾
只含有_______未知数(元),未知数的次数都是____,且等式两边都是_______的方程叫作一元一次方程.
下列式子中,是一元一次方程的是_______(填序号).
① x-2= ;② 0.3x=1;③ =5x+1;④ x2-4x=3;
⑤ x=6;⑥ x+2y=0.
一个
1
整式
②③⑤
探索新知
问题1:“鸡兔同笼”是我国古代数学著作《孙子算经》上的一道题. 今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.
思考1:如何列一元一次方程?
解:设鸡有x只,则兔有(35-x)只.
2x+4(35-x)=94
思考2:问题中有两个未知数,能不能根据题意直接设两个未知数,使列方程变得容易呢?
分析:
鸡的只数+兔的只数=总头数
鸡的脚数+兔的脚数=总脚数
解:设鸡有x只,兔有y只.
鸡 兔 合计
头数 x y 35
脚数 2x 4y 94
x+y=35
2x+4y=94
x+y=35
2x+4y=94
观察下面的方程:
2.它与你学过的一元一次方程比较有什么区别?
1.它们有什么共同特征?
3.你能给它起个名字吗?
定义:含有两个未知数的一次方程叫作二元一次方程.
注意:
1.是整式方程;
2.只含有两个未知数,且未知数的系数不为0;
3. “一次”是指含未知数的项的次数是1,而不是未知数的次数.
x+y=35
2x+4y=94
二元一次方程
三者缺一不可!
下列式子中,是二元一次方程的是_______(填序号).
① 8x-y=3y;② 3x-z=y;③ 2x-5=3;④ +y=2;
⑤ xy=2;⑥ 3x2+1=y;⑦ x-y= .
练一练
判断一个方程是否为二元一次方程的方法:
1.原方程是否是整式方程且只含有两个未知数;
2.整理化简后的方程中两个未知数的系数都不为0,且含未知数的项的次数都是1.
①⑦
x+y=35
2x+4y=94
①
②
几个方程联立在一起,称为方程组.
两个或两个以上
定义:由两个一次方程组成,且含两个未知数的方程组叫作二元一次方程组.
注意:
1.组成方程组的方程都是整式方程;
2.两个方程共含有两个未知数;
3.方程组中含有未知数的项的次数必须都是1.
下列方程组中,是二元一次方程组的是( )
练一练
A. B. C. D.
看两个方程是否为整式方程
看方程组是否一共含有两个未知数
看含未知数的项的次数是否都是1
C
问题2:某班同学在植树节时植樟树和白杨树共50棵. 已知樟树苗每棵10元,白杨树苗每棵3元,购买这些树苗用了290元.樟树苗、白杨树苗各买了多少棵
设樟树苗买了x棵,白杨树苗买了y棵,可得二元一次方程组
x+y=50,
10x+3y=290.
①
②
随堂练习
1.已知2xa-5-(b-2)y|b|-1=4是关于x,y的二元一次方程,则
a-2b=________.
10
2.若 是关于x,y的二元一次方程组,则
a=________,b=________.
﹣1
5
3.根据题意,列出二元一次方程组:
(1)小华买了60分与80分的邮票共10枚,花了7元2角,那么60分和80分的邮票各买了多少枚
【教材P109 练习 第1题】
解:设买了x枚60分的邮票和y枚80分的邮票.
根据题意,得
(2)植树节七(1)班和七(2)班共植树138棵,七(1)班植树数量比七(2)班的 多8棵. 两班分别植树多少棵
解:设七(1)班植树x棵,七(2)班植树y棵.
根据题意,得
(3)将一摞笔记本分给若干同学. 每个同学5本,则剩下8本;每个同学8本,又差了7本. 共有多少本笔记本、多少个同学
解:设共有x本笔记本,y个同学.
根据题意,得
4.请你根据生活实例,编一道应用二元一次方程组的问题,并列出方程组.
解:答案不唯一,如:某船的载重为260t,容积为1000m3. 现有甲、乙两种货物要运,其中甲种货物每吨体积为8m3,乙种货物每吨体积为2m3,若要充分利用这艘船的载重与容积,则甲、乙两种货物应各装多少吨(装运货物时不留空隙)?
设甲、乙两种货物应各装x t,y t.
根据题意,得
【教材P109 练习 第2题】
1星题 基础练
知识点1 二元一次方程
1.[2025·杭州月考]下列方程是二元一次方程的是( )
C
A. B.
C. D.
2.关于,的方程是二元一次方程,则
的取值范围是( )
C
A. B. C. D.
3.若方程是关于, 的二元一次方程,则
___.
3
知识点2 二元一次方程组
4.下列方程组是二元一次方程组的是( )
C
A. B.
C. D.
5.创新题·新考法 若方程组 是二元一次方程组,
则“……”不可能是( )
C
A. B. C. D.
6.[2025年1月安庆期末]若是关于,
的二元一次方程组,则___, ____.
1
知识点3 建立二元一次方程组模型
7.某班35名学生共种87棵树苗.其中男生每人种3棵,女生每
人种2棵,设该班男生有人,女生有 人.根据题意,所列方
程组正确的是( )
D
A. B.
C. D.
8.(8分)教材改编题 根据题意列二元一次方程组.
(1)一个长方形的周长是,宽比长短 ,求这个长方
形的长和宽.
解:设这个长方形的长为,宽为 ,则
(2)某校有两种类型的学生宿舍共30间,大宿舍每间可住8人,
小宿舍每间可住5人,该校住宿生198人恰好住满这30间宿舍,
大、小宿舍各有多少间?
设大宿舍有间,小宿舍有间,则
2星题 中档练
9.易错题 [2024·合肥庐阳区期末] 若方程
是关于,的二元一次方程,则 的值
为( )
D
A. B. C.0 D.1
10.已知方程组:
下列说法正确的是( )
D
A.只有①是二元一次方程组
B.只有②是二元一次方程组
C.只有②③是二元一次方程组
D.只有②不是二元一次方程组
11.数学文化 [2025年1月阜阳期
末] 《九章算术》中的“方程”
一章中讲述了算筹图,如图①②
所示,图中各行从左到右列出的算筹数分别表示未知数,
的系数与相应的常数项,图①表示的算筹图用我们现在所熟
悉的方程组形式表述出来为 类似地,图②所
示的算筹图用方程组可表述为
_ ______________.
12.若 ,则可转化为方程组:
_ ________________.
13.创新题·新考法 问题:“小明家离学校 ,其中有一
段为上坡路,另一段为下坡路.他跑步去学校共用时 ,
已知小明上坡的平均速度为 ,下坡的平均速度为
,小明上坡和下坡各用了多长时间?”
小亮设出未知数,后列出了方程组
则“……”表示的方程是___________,小颖设出未知数,
后却列了和小亮不同的方程组: 则“……”
表示的方程是___________________________.
14.(8分)[2025年1月芜湖期末]如图是
由截面为同一种长方形的墙砖组成的部
分墙面,其中3块横放的墙砖比1块竖放
的墙砖高,2块横放的墙砖比2块竖放的墙砖低 ,
试求每块墙砖截面的长和宽.若设每块墙砖的截面的长为
,宽为 ,请根据题意,列出二元一次方程组.
解:由“3块横放的墙砖比1块竖放的墙砖
高”得 .由“2块横放的墙
砖比2块竖放的墙砖低 ”得
.故可列出二元一次方程组
为
3星题 提升练
15.跨学科·语文 成语“朝三暮四”讲述了一位老翁喂养猴子的故事,老翁为
了限定猴子的食量分早晚两次投喂,早上的粮食是晚上的 ,猴子们对于
这个安排很不满意,于是老翁进行调整,从晚上的粮食中取2千克放在早
上投喂,这样早上的粮食是晚上的 ,猴子们对这样的安排非常满意.设调
整前早上的粮食是千克,晚上的粮食是 千克,则可列方程组为( )
A. B. C. D.
B
课堂小结
二元一次方程组
二元一次方程及二元一次方程组的定义
根据实际问题列二元一次方程组
含有两个未知数的一次方程叫作二元一次方程.
由两个一次方程组成,且含两个未知数的方程组叫作二元一次方程组.
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
