3.4.4选择合适的方法解方程组 课件(共34张PPT)
文档属性
| 名称 | 3.4.4选择合适的方法解方程组 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
3.4.4选择合适的方法解方程组
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
3.4.4 选择合适的方法解方程组
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
前面我们学习了两种解二元一次方程组的方法 —— 代入消元法和加减消元法。代入消元法是将一个未知数用含另一个未知数的式子表示后代入另一个方程;加减消元法是通过将两个方程相加或相减消去一个未知数。这两种方法各有特点,在实际解题中,我们需要根据方程组的具体情况选择合适的方法,以提高解题效率。
学习目标
进一步巩固代入消元法和加减消元法的解题步骤和适用条件。
能根据二元一次方程组的特点,灵活选择代入消元法或加减消元法求解,提高解题的准确性和效率。
培养观察、分析和判断能力,体会数学方法的灵活性和多样性。
方法对比与选择技巧
代入消元法适用情况
当方程组中存在一个未知数的系数为 1 或 - 1 时,优先考虑代入消元法。此时,用含另一个未知数的式子表示该未知数会非常简便,能减少计算量。
例如:方程组\(\begin{cases}y = 2x - 3\\3x + 2y = 8\end{cases}\)中,第一个方程里\(y\)的系数是 1,适合用代入消元法。
加减消元法适用情况
当方程组中两个方程的同一未知数的系数相等或互为相反数时,直接使用加减消元法,可快速消去该未知数。
当方程组中同一未知数的系数成倍数关系,或通过简单变形(两边同乘一个数)能使同一未知数的系数相等或互为相反数时,选择加减消元法更合适。
例如:方程组\(\begin{cases}2x + 3y = 11\\5x - 3y = 1\end{cases}\)中,\(y\)的系数分别是 3 和 - 3,互为相反数,适合用加减消元法;方程组\(\begin{cases}3x + 4y = 16\\5x - 6y = 33\end{cases}\)通过变形可使\(y\)的系数变为 12 和 - 12,也适合用加减消元法。
例题解析
例 1:解方程组\(\begin{cases}x - 2y = 3\\3x + y = 2\end{cases}\)
分析:第二个方程中\(y\)的系数是 1,适合用代入消元法。
解:由②得:\(y = 2 - 3x\) ③
把③代入①得:\(x - 2(2 - 3x)=3\)\(
\begin{align*}
x - 4 + 6x&=3\\
7x&=7\\
x&=1
\end{align*}
\)
把\(x = 1\)代入③得:\(y = 2 - 3 1=-1\)
所以,方程组的解是\(\begin{cases}x = 1\\y = -1\end{cases}\)
例 2:解方程组\(\begin{cases}4x + 5y = 19\\4x - 3y = 3\end{cases}\)
分析:两个方程中\(x\)的系数都是 4,相等,适合用加减消元法。
解:① - ②得:\(
\begin{align*}
(4x + 5y)-(4x - 3y)&=19 - 3\\
8y&=16\\
y&=2
\end{align*}
\)
把\(y = 2\)代入②得:\(4x - 3 2 = 3\)\(
\begin{align*}
4x - 6&=3\\
4x&=9\\
x&=\frac{9}{4}
\end{align*}
\)
所以,方程组的解是\(\begin{cases}x=\frac{9}{4}\\y = 2\end{cases}\)
例 3:解方程组\(\begin{cases}3x - 2y = 5\\5x + 4y = 12\end{cases}\)
分析:\(y\)的系数分别是 - 2 和 4,成倍数关系,把第一个方程两边同乘 2,可使\(y\)的系数变为 - 4 和 4,适合用加减消元法。
解:①×2 得:\(6x - 4y = 10\) ③
② + ③得:\(
\begin{align*}
5x + 4y + 6x - 4y&=12 + 10\\
11x&=22\\
x&=2
\end{align*}
\)
把\(x = 2\)代入①得:\(3 2 - 2y = 5\)\(
\begin{align*}
6 - 2y&=5\\
-2y&=-1\\
y&=\frac{1}{2}
\end{align*}
\)
所以,方程组的解是\(\begin{cases}x = 2\\y=\frac{1}{2}\end{cases}\)
例 4:解方程组\(\begin{cases}\frac{x}{3}+\frac{y}{4}=1\\\frac{x}{2}-\frac{y}{3}=-1\end{cases}\)
分析:先将方程组去分母化为整数系数方程组,再观察选择方法。
解:原方程组去分母(两边同乘 12 和 6 的最小公倍数 12)得:\(\begin{cases}4x + 3y = 12& \\6x - 4y = -12& \end{cases}\)
观察发现,\(x\)和\(y\)的系数无明显简单关系,选择消去\(y\):
①×4 得:\(16x + 12y = 48\) ③
②×3 得:\(18x - 12y = -36\) ④
③ + ④得:\(
\begin{align*}
34x&=12\\
x&=\frac{6}{17}
\end{align*}
\)
把\(x=\frac{6}{17}\)代入①得:\(4 \frac{6}{17}+3y = 12\)\(
\begin{align*}
\frac{24}{17}+3y&=12\\
3y&=12-\frac{24}{17}\\
3y&=\frac{204 - 24}{17}\\
3y&=\frac{180}{17}\\
y&=\frac{60}{17}
\end{align*}
\)
所以,方程组的解是\(\begin{cases}x=\frac{6}{17}\\y=\frac{60}{17}\end{cases}\)
易错点分析
代入时漏乘系数:例如,将\(y = 2x - 1\)代入\(3x + 2y = 5\)时,误写成\(3x + 2x - 1 = 5\),遗漏系数 2 与\(2x\)的乘法。
加减时符号错误:例如,方程组\(\begin{cases}2x + 3y = 7\\3x - 3y = 8\end{cases}\)相加时,误算为\(5x = -1\),忽略\(-3y\)与\(+3y\)相加为 0 的正确结果。
变形后系数计算错误:例如,将方程\(2x - 5y = 3\)两边同乘 3 时,误写成\(6x - 5y = 9\),忘记给\(-5y\)乘 3。
实战练习
解下列方程组,选择合适的方法:
(1)\(\begin{cases}y = 3x - 1\\2x + 3y = 8\end{cases}\)
(2)\(\begin{cases}3x + 2y = 10\\5x - 2y = 6\end{cases}\)
(3)\(\begin{cases}4x - 3y = 5\\2x + 5y = 12\end{cases}\)
(4)\(\begin{cases}\frac{x}{2}+\frac{y}{3}=5\\3x - 2y = 6\end{cases}\)
已知方程组\(\begin{cases}ax + by = 2\\bx + ay = -3\end{cases}\)的解是\(\begin{cases}x = 1\\y = -2\end{cases}\),求\(a\)和\(b\)的值,并用合适的方法解方程组\(\begin{cases}a(x + y)+b(x - y)=2\\b(x + y)+a(x - y)=-3\end{cases}\)
课堂总结
方法选择核心:观察方程组中未知数的系数特点,系数为 1 或 - 1 优先用代入法;系数相等、相反或易变形为上述情况优先用加减法。
解题原则:尽量避免复杂计算(如分数运算),选择步骤最少、最不易出错的方法。
检验习惯:解完方程组后,务必将结果代入原方程组检验,确保解的正确性。
通过本节课的学习,相信你能根据方程组的特点快速判断并选择最优解法,让解方程组的过程更高效、更准确。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
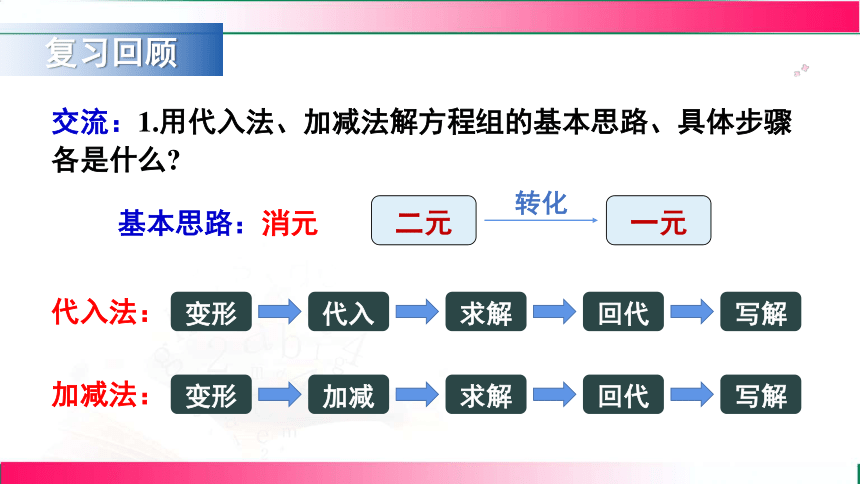
复习回顾
交流:1.用代入法、加减法解方程组的基本思路、具体步骤各是什么
基本思路:消元
二元
一元
转化
代入法:
变形
代入
求解
回代
写解
加减法:
变形
加减
求解
回代
写解
交流:2.用代入法、加减法解题时各应注意些什么?
用代入法解二元一次方程组的变形技巧:
1.当方程组中含有用一个未知数表示另一个未知数的关系式时,直接代入;
2.当方程组中有未知数的系数为1或﹣1时,选择系数为 1或﹣1的方程进行变形;
3.当未知数的系数都不是1或﹣1时,一般选择未知数系数 的绝对值小的方程变形.
交流:2.用代入法、加减法解题时各应注意些什么?
用加减法解二元一次方程组的变形技巧:
1.当某个未知数的系数的绝对值相等时,直接相加减消去该未知数;
2.当某个未知数的系数成整数倍时,消去该未知数;
3.当两个未知数的系数都成整数倍或者系数的绝对值既不相等,也不成整数倍时,常消去系数绝对值的最小公倍数较小的那个未知数.
探索新知
例4:解方程组:
【教材P115 例4】
2(x-150)=5(3y+50),
①
②
10%·x+6%·y=8.5%×800.
加减法?
代入法?
2(x-150)=5(3y+50),
①
②
10%·x+6%·y=8.5%×800.
解:将原方程组化简,得
③+④×5,得27x=17550.
x=650.
将x=650代入④得,5×650+3y=3400.
y=50.
所以
解方程组:
练一练
解:原方程组整理得
②-①,得4y=-16,解得y=-4.
将y=-4代入①,得2x+4=16,解得x=6.
故原方程组的解为
(1)
(2)
随堂练习
1.解下列方程组:
(3)
(4)
【教材P115 练习 第1题】
(1)
解:将原方程组化简,得
②×3,得18x-9y=12.③
③-①,得10x=10. x=1.
把x=1代入②,得6-3y=4. y= .
所以
(2)
解:将原方程组化简,得
②×3,得12m+n=24.③
③-①,得5m=0. m=0.
把m=0代入①,得n=24.
所以
(3)
解:①+②,得16(x+y)=64,即x+y=4.③
①-②,得2(x-y)=-4,即x-y=-2.④
③+④,得2x=2. x=1.
把x=1代入③,得1+y=4. y=3.
所以
①
②
(4)
解:将原方程组化简,得
②-①,得y=20-60. y=-40.
把y=-40代入①,得x-40=60. x=100.
所以
2.解方程组:
解:设x+y=A,x-y=B,则原方程组可变形为
解得
所以
解得
我们把某个式子看成一个整体,用一个字母去代替它,这种解方程组的方法叫作“换元法”.
3.已知关于x,y的二元一次方程(3x-2y+9)+m(2x+y-1)=0,不论m取何值,方程总有一个固定不变的解,这个解是多少?
解:不论m取何值,方程(3x-2y+9)+m(2x+y-1)=0总有一个固定不变的解,与m的值无关,则这个解满足2x+y-1=0,因而
3x-2y+9=0,解方程组 得
解法1 代入消元法
1.(12分)[2025年1月合肥期末]用代入消元法解下列方程组.
(1)
解:把①代入②,得 ,
解得.把代入①,得 .所以原方程组的解为
(2)
解:由①,得 ,③
把③代入②,得,解得 .
将代入③,得 ,
所以原方程组的解为
(3)
解:原方程组整理为
由②,得 .③
将③代入①,得,解得,将
代入③,得,所以原方程组的解为
解法2 加减消元法
2.(12分)用加减消元法解下列方程组.
(1)
解:,得,解得.把 代入①,得
,解得.所以原方程组的解为
(2)
解:,得 .③
,得,解得 .
把代入①,得,解得 .
所以原方程组的解为
(3)
解:,得 .③
,得 .④
解由③④构成的方程组,可得
解法3 整体代入法
3.(14分) 如何解方程组:
解法4 整体加减法
4.(8分)解方程组:
解:并化简,得 .③
分别把③代入①和②,求得, .所以原方程组的解
为
解法5 换元法
5.(8分)解方程组:
解:令,.则原方程组可变为
解得即
解得
解法6 用适当的方法解二元一次方程组
6.(12分)中考趋势·阅读理解
(1)仔细阅读下面解方程组的方法,并将解题过程补充完整:
解方程组 时,直接采用代入消元法或加
减消元法,计算会很复杂,若采用下面的解法,则会简单很多.
解:,得,即 ,③
,得 ,④
,得 ____.
将____代入③,得 ___.
所以方程组的解为_ ________;
2
(2)请你采用上述方法解方程组:
解:,得,即 ,③
,得 ,④
,得.将代入③,得 ,
所以原方程组的解为
(3)探究:求关于, 的方程组
的解其中 .
,得 ,
即 .③
,得 .④
,得.将代入③,得 .
所以原方程组的解为
课堂小结
代入法和加减法是二元一次方程组的两种解法,它们都是通过消元使方程组转化为一元一次方程. 我们应该根据方程组的具体情况,选择合适的解法.
谢谢观看!
3.4.4选择合适的方法解方程组
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
3.4.4 选择合适的方法解方程组
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
前面我们学习了两种解二元一次方程组的方法 —— 代入消元法和加减消元法。代入消元法是将一个未知数用含另一个未知数的式子表示后代入另一个方程;加减消元法是通过将两个方程相加或相减消去一个未知数。这两种方法各有特点,在实际解题中,我们需要根据方程组的具体情况选择合适的方法,以提高解题效率。
学习目标
进一步巩固代入消元法和加减消元法的解题步骤和适用条件。
能根据二元一次方程组的特点,灵活选择代入消元法或加减消元法求解,提高解题的准确性和效率。
培养观察、分析和判断能力,体会数学方法的灵活性和多样性。
方法对比与选择技巧
代入消元法适用情况
当方程组中存在一个未知数的系数为 1 或 - 1 时,优先考虑代入消元法。此时,用含另一个未知数的式子表示该未知数会非常简便,能减少计算量。
例如:方程组\(\begin{cases}y = 2x - 3\\3x + 2y = 8\end{cases}\)中,第一个方程里\(y\)的系数是 1,适合用代入消元法。
加减消元法适用情况
当方程组中两个方程的同一未知数的系数相等或互为相反数时,直接使用加减消元法,可快速消去该未知数。
当方程组中同一未知数的系数成倍数关系,或通过简单变形(两边同乘一个数)能使同一未知数的系数相等或互为相反数时,选择加减消元法更合适。
例如:方程组\(\begin{cases}2x + 3y = 11\\5x - 3y = 1\end{cases}\)中,\(y\)的系数分别是 3 和 - 3,互为相反数,适合用加减消元法;方程组\(\begin{cases}3x + 4y = 16\\5x - 6y = 33\end{cases}\)通过变形可使\(y\)的系数变为 12 和 - 12,也适合用加减消元法。
例题解析
例 1:解方程组\(\begin{cases}x - 2y = 3\\3x + y = 2\end{cases}\)
分析:第二个方程中\(y\)的系数是 1,适合用代入消元法。
解:由②得:\(y = 2 - 3x\) ③
把③代入①得:\(x - 2(2 - 3x)=3\)\(
\begin{align*}
x - 4 + 6x&=3\\
7x&=7\\
x&=1
\end{align*}
\)
把\(x = 1\)代入③得:\(y = 2 - 3 1=-1\)
所以,方程组的解是\(\begin{cases}x = 1\\y = -1\end{cases}\)
例 2:解方程组\(\begin{cases}4x + 5y = 19\\4x - 3y = 3\end{cases}\)
分析:两个方程中\(x\)的系数都是 4,相等,适合用加减消元法。
解:① - ②得:\(
\begin{align*}
(4x + 5y)-(4x - 3y)&=19 - 3\\
8y&=16\\
y&=2
\end{align*}
\)
把\(y = 2\)代入②得:\(4x - 3 2 = 3\)\(
\begin{align*}
4x - 6&=3\\
4x&=9\\
x&=\frac{9}{4}
\end{align*}
\)
所以,方程组的解是\(\begin{cases}x=\frac{9}{4}\\y = 2\end{cases}\)
例 3:解方程组\(\begin{cases}3x - 2y = 5\\5x + 4y = 12\end{cases}\)
分析:\(y\)的系数分别是 - 2 和 4,成倍数关系,把第一个方程两边同乘 2,可使\(y\)的系数变为 - 4 和 4,适合用加减消元法。
解:①×2 得:\(6x - 4y = 10\) ③
② + ③得:\(
\begin{align*}
5x + 4y + 6x - 4y&=12 + 10\\
11x&=22\\
x&=2
\end{align*}
\)
把\(x = 2\)代入①得:\(3 2 - 2y = 5\)\(
\begin{align*}
6 - 2y&=5\\
-2y&=-1\\
y&=\frac{1}{2}
\end{align*}
\)
所以,方程组的解是\(\begin{cases}x = 2\\y=\frac{1}{2}\end{cases}\)
例 4:解方程组\(\begin{cases}\frac{x}{3}+\frac{y}{4}=1\\\frac{x}{2}-\frac{y}{3}=-1\end{cases}\)
分析:先将方程组去分母化为整数系数方程组,再观察选择方法。
解:原方程组去分母(两边同乘 12 和 6 的最小公倍数 12)得:\(\begin{cases}4x + 3y = 12& \\6x - 4y = -12& \end{cases}\)
观察发现,\(x\)和\(y\)的系数无明显简单关系,选择消去\(y\):
①×4 得:\(16x + 12y = 48\) ③
②×3 得:\(18x - 12y = -36\) ④
③ + ④得:\(
\begin{align*}
34x&=12\\
x&=\frac{6}{17}
\end{align*}
\)
把\(x=\frac{6}{17}\)代入①得:\(4 \frac{6}{17}+3y = 12\)\(
\begin{align*}
\frac{24}{17}+3y&=12\\
3y&=12-\frac{24}{17}\\
3y&=\frac{204 - 24}{17}\\
3y&=\frac{180}{17}\\
y&=\frac{60}{17}
\end{align*}
\)
所以,方程组的解是\(\begin{cases}x=\frac{6}{17}\\y=\frac{60}{17}\end{cases}\)
易错点分析
代入时漏乘系数:例如,将\(y = 2x - 1\)代入\(3x + 2y = 5\)时,误写成\(3x + 2x - 1 = 5\),遗漏系数 2 与\(2x\)的乘法。
加减时符号错误:例如,方程组\(\begin{cases}2x + 3y = 7\\3x - 3y = 8\end{cases}\)相加时,误算为\(5x = -1\),忽略\(-3y\)与\(+3y\)相加为 0 的正确结果。
变形后系数计算错误:例如,将方程\(2x - 5y = 3\)两边同乘 3 时,误写成\(6x - 5y = 9\),忘记给\(-5y\)乘 3。
实战练习
解下列方程组,选择合适的方法:
(1)\(\begin{cases}y = 3x - 1\\2x + 3y = 8\end{cases}\)
(2)\(\begin{cases}3x + 2y = 10\\5x - 2y = 6\end{cases}\)
(3)\(\begin{cases}4x - 3y = 5\\2x + 5y = 12\end{cases}\)
(4)\(\begin{cases}\frac{x}{2}+\frac{y}{3}=5\\3x - 2y = 6\end{cases}\)
已知方程组\(\begin{cases}ax + by = 2\\bx + ay = -3\end{cases}\)的解是\(\begin{cases}x = 1\\y = -2\end{cases}\),求\(a\)和\(b\)的值,并用合适的方法解方程组\(\begin{cases}a(x + y)+b(x - y)=2\\b(x + y)+a(x - y)=-3\end{cases}\)
课堂总结
方法选择核心:观察方程组中未知数的系数特点,系数为 1 或 - 1 优先用代入法;系数相等、相反或易变形为上述情况优先用加减法。
解题原则:尽量避免复杂计算(如分数运算),选择步骤最少、最不易出错的方法。
检验习惯:解完方程组后,务必将结果代入原方程组检验,确保解的正确性。
通过本节课的学习,相信你能根据方程组的特点快速判断并选择最优解法,让解方程组的过程更高效、更准确。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
复习回顾
交流:1.用代入法、加减法解方程组的基本思路、具体步骤各是什么
基本思路:消元
二元
一元
转化
代入法:
变形
代入
求解
回代
写解
加减法:
变形
加减
求解
回代
写解
交流:2.用代入法、加减法解题时各应注意些什么?
用代入法解二元一次方程组的变形技巧:
1.当方程组中含有用一个未知数表示另一个未知数的关系式时,直接代入;
2.当方程组中有未知数的系数为1或﹣1时,选择系数为 1或﹣1的方程进行变形;
3.当未知数的系数都不是1或﹣1时,一般选择未知数系数 的绝对值小的方程变形.
交流:2.用代入法、加减法解题时各应注意些什么?
用加减法解二元一次方程组的变形技巧:
1.当某个未知数的系数的绝对值相等时,直接相加减消去该未知数;
2.当某个未知数的系数成整数倍时,消去该未知数;
3.当两个未知数的系数都成整数倍或者系数的绝对值既不相等,也不成整数倍时,常消去系数绝对值的最小公倍数较小的那个未知数.
探索新知
例4:解方程组:
【教材P115 例4】
2(x-150)=5(3y+50),
①
②
10%·x+6%·y=8.5%×800.
加减法?
代入法?
2(x-150)=5(3y+50),
①
②
10%·x+6%·y=8.5%×800.
解:将原方程组化简,得
③+④×5,得27x=17550.
x=650.
将x=650代入④得,5×650+3y=3400.
y=50.
所以
解方程组:
练一练
解:原方程组整理得
②-①,得4y=-16,解得y=-4.
将y=-4代入①,得2x+4=16,解得x=6.
故原方程组的解为
(1)
(2)
随堂练习
1.解下列方程组:
(3)
(4)
【教材P115 练习 第1题】
(1)
解:将原方程组化简,得
②×3,得18x-9y=12.③
③-①,得10x=10. x=1.
把x=1代入②,得6-3y=4. y= .
所以
(2)
解:将原方程组化简,得
②×3,得12m+n=24.③
③-①,得5m=0. m=0.
把m=0代入①,得n=24.
所以
(3)
解:①+②,得16(x+y)=64,即x+y=4.③
①-②,得2(x-y)=-4,即x-y=-2.④
③+④,得2x=2. x=1.
把x=1代入③,得1+y=4. y=3.
所以
①
②
(4)
解:将原方程组化简,得
②-①,得y=20-60. y=-40.
把y=-40代入①,得x-40=60. x=100.
所以
2.解方程组:
解:设x+y=A,x-y=B,则原方程组可变形为
解得
所以
解得
我们把某个式子看成一个整体,用一个字母去代替它,这种解方程组的方法叫作“换元法”.
3.已知关于x,y的二元一次方程(3x-2y+9)+m(2x+y-1)=0,不论m取何值,方程总有一个固定不变的解,这个解是多少?
解:不论m取何值,方程(3x-2y+9)+m(2x+y-1)=0总有一个固定不变的解,与m的值无关,则这个解满足2x+y-1=0,因而
3x-2y+9=0,解方程组 得
解法1 代入消元法
1.(12分)[2025年1月合肥期末]用代入消元法解下列方程组.
(1)
解:把①代入②,得 ,
解得.把代入①,得 .所以原方程组的解为
(2)
解:由①,得 ,③
把③代入②,得,解得 .
将代入③,得 ,
所以原方程组的解为
(3)
解:原方程组整理为
由②,得 .③
将③代入①,得,解得,将
代入③,得,所以原方程组的解为
解法2 加减消元法
2.(12分)用加减消元法解下列方程组.
(1)
解:,得,解得.把 代入①,得
,解得.所以原方程组的解为
(2)
解:,得 .③
,得,解得 .
把代入①,得,解得 .
所以原方程组的解为
(3)
解:,得 .③
,得 .④
解由③④构成的方程组,可得
解法3 整体代入法
3.(14分) 如何解方程组:
解法4 整体加减法
4.(8分)解方程组:
解:并化简,得 .③
分别把③代入①和②,求得, .所以原方程组的解
为
解法5 换元法
5.(8分)解方程组:
解:令,.则原方程组可变为
解得即
解得
解法6 用适当的方法解二元一次方程组
6.(12分)中考趋势·阅读理解
(1)仔细阅读下面解方程组的方法,并将解题过程补充完整:
解方程组 时,直接采用代入消元法或加
减消元法,计算会很复杂,若采用下面的解法,则会简单很多.
解:,得,即 ,③
,得 ,④
,得 ____.
将____代入③,得 ___.
所以方程组的解为_ ________;
2
(2)请你采用上述方法解方程组:
解:,得,即 ,③
,得 ,④
,得.将代入③,得 ,
所以原方程组的解为
(3)探究:求关于, 的方程组
的解其中 .
,得 ,
即 .③
,得 .④
,得.将代入③,得 .
所以原方程组的解为
课堂小结
代入法和加减法是二元一次方程组的两种解法,它们都是通过消元使方程组转化为一元一次方程. 我们应该根据方程组的具体情况,选择合适的解法.
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
