3.5.2百分率与方案问题 课件(共35张PPT)
文档属性
| 名称 | 3.5.2百分率与方案问题 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览











文档简介
(共35张PPT)
3.5.2百分率与方案问题
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
3.5.2 百分率与方案问题
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
上一节课我们学习了用二元一次方程组解决比赛得分与行程问题,体会到了方程组在解决实际问题中的作用。今天我们将继续学习另外两类重要的实际问题 —— 百分率问题和方案问题。百分率问题在经济增长、浓度配比等场景中十分常见,方案问题则能帮助我们在多种选择中找到最优解,掌握这两类问题的解法对我们解决实际生活中的数学问题有着重要意义。
学习目标
理解百分率问题的含义,掌握增长率、浓度等问题的基本数量关系,能运用二元一次方程组解决相关问题。
学会分析方案问题中的数量关系,能根据不同的条件列出方程组,进而比较和选择最优方案。
进一步提高从实际问题中抽象出数学模型的能力,增强运用数学知识解决实际问题的意识和能力。
知识点:百分率问题
百分率问题主要涉及增长率、下降率、浓度等,核心是围绕 “基础量 ×(1 + 百分率)= 增长后量”“基础量 ×(1 - 百分率)= 下降后量” 等数量关系展开。
常见类型及数量关系
增长率问题:
原量 ×(1 + 增长率)= 新量
若涉及两个连续增长阶段,且增长率不同,设第一阶段增长率为\(x\),第二阶段增长率为\(y\),则原量 ×(1 + \(x\))×(1 + \(y\))= 最终量
浓度问题:
浓度 = \(\frac{ è ¨è ¨é }{ è ¨é }\)×100%
溶质质量 = 溶液质量 × 浓度
混合前溶质质量之和 = 混合后溶质质量
混合前溶液质量之和 = 混合后溶液质量
例题解析
例 1:某工厂去年的利润(总收入 - 总支出)为 200 万元,今年总收入比去年增加了 20%,总支出比去年减少了 10%,今年的利润为 780 万元,问去年的总收入、总支出各是多少万元?
解:审:已知去年利润 200 万元,今年总收入增 20%,总支出减 10%,今年利润 780 万元,求去年的总收入和总支出。
设:设去年的总收入为\(x\)万元,总支出为\(y\)万元。
找:等量关系有两个,一是 “去年总收入 - 去年总支出 = 去年利润”,二是 “今年总收入 - 今年总支出 = 今年利润”。
列:根据等量关系,列出方程组:\(\begin{cases}x - y = 200\\(1 + 20\%)x-(1 - 10\%)y = 780\end{cases}\)
化简第二个方程:\(1.2x - 0.9y = 780\)
解:由第一个方程得\(x = y + 200\) ③,把③代入第二个方程:\(
\begin{align*}
1.2(y + 200)-0.9y&=780\\
1.2y + 240 - 0.9y&=780\\
0.3y&=540\\
y&=1800
\end{align*}
\)
把\(y = 1800\)代入③得:\(x = 1800 + 200 = 2000\)。
验:去年总收入 2000 万元,总支出 1800 万元,利润\(2000 - 1800 = 200\)万元;今年总收入\(2000 1.2 = 2400\)万元,总支出\(1800 0.9 = 1620\)万元,利润\(2400 - 1620 = 780\)万元,符合题意。
答:去年的总收入是 2000 万元,总支出是 1800 万元。
例 2:有两种酒精溶液,甲种酒精溶液的浓度为 30%,乙种酒精溶液的浓度为 60%,现要配制浓度为 50% 的酒精溶液 300 克,问需要甲、乙两种酒精溶液各多少克?
解:审:甲浓度 30%,乙浓度 60%,要配浓度 50% 的溶液 300 克,求甲、乙各需多少克。
设:设需要甲种酒精溶液\(x\)克,乙种酒精溶液\(y\)克。
找:等量关系有 “甲溶液质量 + 乙溶液质量 = 混合后溶液质量” 和 “甲溶液中溶质质量 + 乙溶液中溶质质量 = 混合后溶液中溶质质量”。
列:根据等量关系,列出方程组:\(\begin{cases}x + y = 300\\30\%x + 60\%y = 50\% 300\end{cases}\)
化简第二个方程:\(0.3x + 0.6y = 150\),两边同除以 0.3 得\(x + 2y = 500\) ②
解:用② - ①得:\(y = 200\)
把\(y = 200\)代入①得:\(x = 300 - 200 = 100\)。
验:甲 100 克含溶质\(100 30\% = 30\)克,乙 200 克含溶质\(200 60\% = 120\)克,混合后溶质共 150 克,溶液 300 克,浓度\(\frac{150}{300} 100\% = 50\%\),符合题意。
答:需要甲种酒精溶液 100 克,乙种酒精溶液 200 克。
知识点:方案问题
方案问题是指根据不同的条件设计多种解决方案,通过计算和比较,选择最优方案(如成本最低、利润最高、效率最高等)。解决这类问题的关键是列出每种方案的数量关系,通过方程组求解后进行对比。
解题步骤
分析题目,确定可能的方案种类。
设出未知数,根据每种方案的条件列出方程组。
解方程组,求出每种方案的相关数据(如成本、利润等)。
比较各种方案的结果,选择最优方案。
例题解析
例 3:某中学计划购买 A、B 两种型号的课桌凳共 200 套,经调查,购买一套 A 型号课桌凳比购买一套 B 型号课桌凳少用 40 元,且购买 4 套 A 型号和 5 套 B 型号课桌凳共需 1820 元。
(1)求购买一套 A 型号、一套 B 型号的课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳的总费用不超过 40880 元,并且购买 A 型号课桌凳的数量不能超过 B 型号课桌凳数量的\(\frac{2}{3}\),求该校本次购买 A、B 两种型号课桌凳共有几种方案?哪种方案的总费用最低?
解:(1)审:A 比 B 每套少 40 元,4 套 A + 5 套 B = 1820 元,求 A、B 单价。
设:设购买一套 A 型号课桌凳需\(x\)元,一套 B 型号课桌凳需\(y\)元。
列:\(\begin{cases}y - x = 40\\4x + 5y = 1820\end{cases}\)
解:由①得\(y = x + 40\) ③,代入②得:\(
\begin{align*}
4x + 5(x + 40)&=1820\\
4x + 5x + 200&=1820\\
9x&=1620\\
x&=180
\end{align*}
\)
把\(x = 180\)代入③得\(y = 220\)。
答:购买一套 A 型号需 180 元,一套 B 型号需 220 元。
(2)审:共买 200 套,总费用≤40880 元,A 数量≤\(\frac{2}{3}\)B 数量,求方案及最低费用。
设:设购买 A 型号课桌凳\(a\)套,则购买 B 型号课桌凳\((200 - a)\)套。
列:根据条件列出不等式组:\(\begin{cases}180a + 220(200 - a) ¤40880\\a ¤\frac{2}{3}(200 - a)\end{cases}\)
解第一个不等式:\(
\begin{align*}
180a + 44000 - 220a& ¤40880\\
-40a& ¤-3120\\
a& 78
\end{align*}
\)
解第二个不等式:\(
\begin{align*}
3a& ¤2(200 - a)\\
3a& ¤400 - 2a\\
5a& ¤400\\
a& ¤80
\end{align*}
\)
所以\(78 ¤a ¤80\),因为\(a\)为整数,所以\(a = 78\)、79、80,共 3 种方案。
方案一:A78 套,B122 套,费用\(180 78 + 220 122 = 14040 + 26840 = 40880\)元;
方案二:A79 套,B121 套,费用\(180 79 + 220 121 = 14220 + 26620 = 40840\)元;
方案三:A80 套,B120 套,费用\(180 80 + 220 120 = 14400 + 26400 = 40800\)元。
比较:40800<40840<40880,方案三费用最低。
答:共有 3 种方案,购买 A 型号 80 套、B 型号 120 套的总费用最低。
例 4:某商场计划用 9 万元从生产厂家购进 50 台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为 A 种每台 1500 元,B 种每台 2100 元,C 种每台 2500 元。
(1)若商场同时购进两种不同型号的电视机共 50 台,用去 9 万元,研究一下商场的进货方案;
(2)若商场销售一台 A 种电视机可获利 150 元,销售一台 B 种电视机可获利 200 元,销售一台 C 种电视机可获利 250 元,在(1)的进货方案中,哪种方案获利最多?
解:(1)分三种情况讨论:
情况一:购进 A、B 两种型号
设购进 A 种\(x\)台,B 种\(y\)台,则\(\begin{cases}x + y = 50\\1500x + 2100y = 90000\end{cases}\)
化简第二个方程:\(5x + 7y = 300\),由①得\(x = 50 - y\),代入得:\(
\begin{align*}
5(50 - y)+7y&=300\\
250 - 5y + 7y&=300\\
2y&=50\\
y&=25
\end{align*}
\)
则\(x = 25\),即购进 A25 台,B25 台。
情况二:购进 A、C 两种型号
设购进 A 种\(m\)台,C 种\(n\)台,则\(\begin{cases}m + n = 50\\1500m + 2500n = 90000\end{cases}\)
化简第二个方程:\(3m + 5n = 180\),由①得\(m = 50 - n\),代入得:\(
\begin{align*}
3(50 - n)+5n&=180\\
150 - 3n + 5n&=180\\
2n&=30\\
n&=15
\end{align*}
\)
则\(m = 35\),即购进 A35 台,C15 台。
情况三:购进 B、C 两种型号
设购进 B 种\(p\)台,C 种\(q\)台,则\(\begin{cases}p + q = 50\\2100p + 2500q = 90000\end{cases}\)
化简第二个方程:\(21p + 25q = 900\),由①得\(p = 50 - q\),代入得:\(
\begin{align*}
21(50 - q)+25q&=900\\
1050 - 21q + 25q&=900\\
4q&=-150\\
q&=-37.5
\end{align*}
\)
台数不能为负数,此情况舍去。
答:进货方案有两种,一是购进 A25 台、B25 台;二是购进 A35 台、C15 台。
(2)计算各方案获利:
方案一获利:\(25 150 + 25 200 = 3750 + 5000 = 8750\)元;
方案二获利:\(35 150 + 15 250 = 5250 + 3750 = 9000\)元。
比较:9000>8750,方案二获利最多。
答:购进 A35 台、C15 台的方案获利最多。
小练习
某工厂第一季度生产甲、乙两种机器共 480 台,改进生产技术后,第二季度生产这两种机器共 554 台,其中甲种机器产量的增长率为 10%,乙种机器产量的增长率为 20%,问该工厂第一季度生产甲、乙两种机器各多少台?
现有含盐 20% 的盐水 500 克,要把它变成含盐 15% 的盐水,应加入含盐 5% 的盐水多少克?
某运输公司有 A、B 两种货车,3 辆 A 货车与 2 辆 B 货车一次可以运货 17 吨,5 辆 A 货车与 4 辆 B 货车一次可以运货 31 吨。
(1)求每辆 A 货车和每辆 B 货车一次分别可以运货多少吨?
(2)现有货物 32 吨,计划同时租用 A 货车和 B 货车,要求一次运完,且每辆车都装满货物,试写出所有的租车方案,并求出最少租车费(已知每辆 A 货车租车费 200 元,每辆 B 货车租车费 300 元)。
思考讨论
解决百分率问题时,如何准确找到等量关系?
解决百分率问题,首先要明确题目中涉及的是哪种类型的百分率(如增长率、浓度等),然后根据对应的基本数量关系(如 “原量 ×(1 + 增长率)= 新量”“溶质质量 = 溶液质量 × 浓度”)来构建等量关系。对于涉及两个未知量的问题,要从题目中找出两个不同的等量关系,从而列出二元一次方程组。例如在增长率问题中,通常可以从 “增长前后的数量关系” 和 “两个不同阶段的增长结果” 这两个角度寻找等量关系。
在方案问题中,如何确保不遗漏任何一种可能的方案?
在方案问题中,首先要明确题目中的限制条件(如数量范围、费用上限等),这些条件往往会确定未知数的取值范围。然后,根据未知数的实际意义(如必须为正整数),在取值范围内找出所有可能的取值,进而确定所有的方案。例如在购买物品的方案问题中,设购买 A 物品\(x\)件,B 物品\(y\)件,根据总数量和总费用的
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
百分率一般表示某部分占总体的多少,由此可以求出该部分的数量,再根据“总量 = 各部分量的和”,可以列出方程组后求解.
探索新知
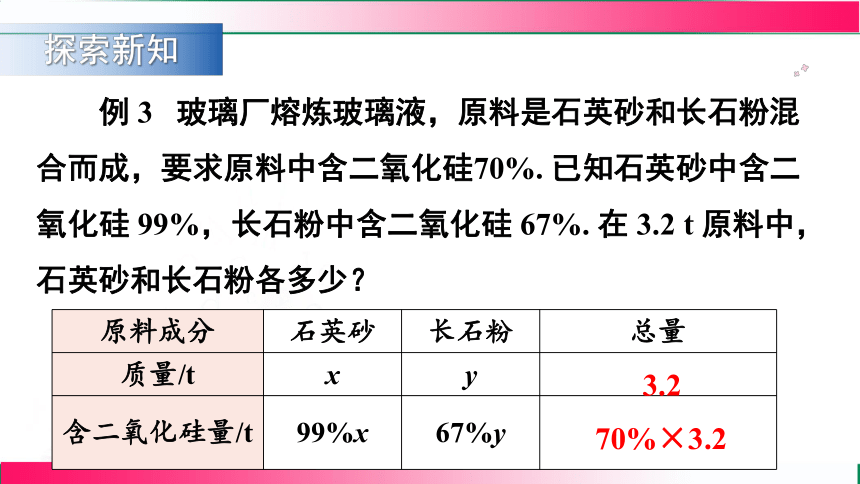
例 3 玻璃厂熔炼玻璃液,原料是石英砂和长石粉混合而成,要求原料中含二氧化硅70%. 已知石英砂中含二氧化硅 99%,长石粉中含二氧化硅 67%. 在 3.2 t 原料中,石英砂和长石粉各多少?
原料成分 石英砂 长石粉 总量
质量/t x y
含二氧化硅量/t 99%x 67%y
3.2
70%×3.2
解 设原料中石英砂 x t,长石粉有 y t. 根据题意,得
x + y = 3.2,
99%x + 67%y = 70%×3.2.
解方程组,得
x = 0.3,
y = 2.9.
答:在 3.2 t 原料中,石英砂有 0.3 t,长石粉有 2.9 t.
百分比问题中常见的是增长(下降)率问题、与浓度有关的问题等,其中增长(下降)率问题中的等量关系如下:
(1)增长率 = ×100%;
增长后的量 – 增长前的量
增长前的量
(2)增长后的量 = 增长前的量×(1 + 增长率);
(3)下降率 = ×100%;
下降前的量 – 下降后的量
下降前的量
(4)下降后的量 = 下降前的量×(1 – 下降率).
巩固练习
某皮鞋厂前年的利润为 100 万元,去年的总产值比前年增加了 20% ,总支出比前年减少了 5% ,去年的利润为 400 万元,那么该皮鞋厂前年的总产值和总支出各是多少万元?
分析:设该皮鞋厂前年的总产值是 x 万元,总支出是 y 万元,
总产值/万元 总支出/万元 利润/万元
前年 x y 100
去年 (1+20%)x (1-5%)y 400
解: 设该皮鞋厂前年的总产值是 x 万元,总支出是 y 万元.
根据题意,得
x - y = 100,
(1+20%)x - (1-5%)y = 400.
解方程组,得
x = 1220,
y = 1120.
答: 该皮鞋厂前年的总产值是 1220 万元,总支出是 1120 万元.
练 习
1. 某乡今年春播作物的面积比秋播作物的面积多 630 hm2.
计划明年春播作物的面积增加 20%,秋播作物的面积减少 10%,这样明年春播、秋播作物的总面积将比今年增加 12%.这个乡今年春播与秋播作物的面积各是多少?
【教材P121 练习 第1题】
解: 设这个乡今年春播作物的面积为 x hm2,秋播作物的面积为 y hm2.
根据题意,得
x - y = 630,
x(1+20%) + y(1-10%) = (x+y)(1+12%).
解方程组,得
x = 990,
y = 360.
答: 这个乡今年春播作物的面积为 990 hm2,秋播作物的面积为 360 hm2.
2. 石岭村原有林地、旱地共 162 hm2. 村里把一部分旱地改造为林地,使旱地面积为林地面积的 20%.
求改造后的旱地面积和林地面积.
解: 设改造后的旱地面积为 x hm2,林地面积为 y hm2.
根据题意,得 解方程组,得
x + y = 162,
x = 20%y.
x = 27,
y = 135.
答: 改造后的旱地面积为 27 hm2,林地面积为 135 hm2.
【教材P121 练习 第2题】
1星题 基础练
知识点1 百分率问题
1.真实情境 某地推广智慧农业技术,将部分传统农田改造为智
能温室种植区.改造后,传统农田面积是智能温室面积的 ,
且传统农田与智能温室总面积为 .设改造后传统农田面
积为,智能温室面积为 ,则可列方程组为 ( )
B
A. B.
C. D.
2.有甲、乙两种铜和银的合金,甲种合金含银 ,乙种合
金含银,现在要熔制含银的合金 ,设需甲
合金的质量为,乙合金的质量为 ,则可列方程组为
_ _____________________________.
3.甲仓库和乙仓库共存粮450吨,现从甲仓库运出存粮的
,从乙仓库运出存粮的 ,结果乙仓库所余的粮食比
甲仓库所余的粮食多30吨.则甲仓库原来存粮_____吨,乙仓库
原来存粮_____吨.
240
210
4.(8分)某校去年有学生1 000名,今年比去年增加了 ,
其中寄宿学生增加了,走读学生减少了 ,问该校去年
有寄宿学生与走读学生各多少名?
解:设该校去年有寄宿学生名,走读学生 名.
根据题意,得
解得
答:该校去年有寄宿学生800名,走读学生200名.
知识点2 方案问题
5.[2025年1月合肥期末]已知1辆 型车载满货物一次可运
货1吨,1辆 型车载满货物一次可运货4吨.某公司有14吨货
物,计划同时租用型车和 型车,一次运完,且每辆车都
装满货物,共有租车方案( )
B
A.4种 B.3种 C.2种 D.1种
6.某校为加强爱读书、读好书、善读书的阅读氛围,准备用
720元购买图书展示架,可供选择的有 种展示架120元/个,
种展示架180元/个,在资金用尽且可以只买其中一种展示
架的情况下,一共有___种购买方案.
3
7.(8分)[2025·广州模拟]某公司组织员工去三星堆参观,现
有,两种客车可以租用.已知3辆种客车和2辆 种客车可
以坐260人,2辆种客车可坐的人数和3辆 种客车可坐的人
数一样多.
(1)请问, 两种客车每辆分别可坐多少人?
解:设种客车每辆可坐人,种客车每辆可坐 人,
根据题意,得解得
答:种客车每辆可坐60人, 种客车每辆可坐40人.
(2)已知该公司共有320名员工,请问如何安排租车方案,可
以使得所有员工恰好坐下?
设租用辆种客车,辆 种客车,根据题意,得
,所以 ,
又因为, 均为非负整数,
所以或或 所以共有3种租车方案,
方案1:租用8辆 种客车;
方案2:租用2辆种客车,5辆 种客车;
方案3:租用4辆种客车,2辆 种客车.
2星题 中档练
8.[2025年1月芜湖期末]某工程公司下属的甲工程队、乙工
程队分别承包了工程、 工程,甲工程队晴天需要14天完
成,雨天工作效率下降 ;乙工程队晴天需要15天完成,
雨天工作效率下降 ,实际上两个工程队同时开工,同时
完工,两个工程队各工作了( )
C
A.15天 B.16天 C.17天 D.18天
设两工程队各工作了天,在施工期间有 天有雨,
由题意得,
解得 故两个工程队各工作了17天.
9.(8分) 真 实 情 境[2025 合肥月考] 点点学校引入 营养
师系统,为学生定制低碳环保早餐套餐.每 早餐套餐中,
蛋白质总含量为 ,包括一个谷物面包,一盒牛奶和一个
去壳鸡蛋(一个去壳鸡蛋的质量约为 ,其中蛋白质含量为
;谷物面包和牛奶的部分主要营养成分如表所示).
项目 谷物面包(含量) 牛奶(含量)
蛋白质
脂肪
碳水化合物
设该早餐套餐中每份有谷物面包,牛奶 .
(1)请补全表格(用含有, 的代数式表示);
谷物面包 牛奶 去壳鸡蛋 总量
50 400
_______ _____ 11
(2)求出, 的值.
解:由题意,得:
解得
3星题 提升练
10.(12分)应用意识 现有若干个体积相同的
大球和体积相同的小球,根据图中的信息,
解答下面的问题:
(1)放入1个小球水面升高___,放入1个大球水面升高___ ;
2
3
(2)如果放入大球、小球共10个,要使水面
上升到 ,应放入大球、小球各多少
个
解:设应放入个大球, 个小球.
根据题意得 解得
答:应放入4个大球,6个小球.
(3)现有充足的大球和小球,要使水面上升到 ,你还有其
他方案吗
设放入个大球, 个小球,根据题意得
,所以 .又
因为,均为非负整数,所以 或
或或或
所以还有4个其他方案,分别为
方案1:放入8个大球;
方案2:放入6个大球,3个小球;
方案3:放入2个大球,9个小球;
方案4:放入12个小球.
谢谢观看!
3.5.2百分率与方案问题
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
3.5.2 百分率与方案问题
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
上一节课我们学习了用二元一次方程组解决比赛得分与行程问题,体会到了方程组在解决实际问题中的作用。今天我们将继续学习另外两类重要的实际问题 —— 百分率问题和方案问题。百分率问题在经济增长、浓度配比等场景中十分常见,方案问题则能帮助我们在多种选择中找到最优解,掌握这两类问题的解法对我们解决实际生活中的数学问题有着重要意义。
学习目标
理解百分率问题的含义,掌握增长率、浓度等问题的基本数量关系,能运用二元一次方程组解决相关问题。
学会分析方案问题中的数量关系,能根据不同的条件列出方程组,进而比较和选择最优方案。
进一步提高从实际问题中抽象出数学模型的能力,增强运用数学知识解决实际问题的意识和能力。
知识点:百分率问题
百分率问题主要涉及增长率、下降率、浓度等,核心是围绕 “基础量 ×(1 + 百分率)= 增长后量”“基础量 ×(1 - 百分率)= 下降后量” 等数量关系展开。
常见类型及数量关系
增长率问题:
原量 ×(1 + 增长率)= 新量
若涉及两个连续增长阶段,且增长率不同,设第一阶段增长率为\(x\),第二阶段增长率为\(y\),则原量 ×(1 + \(x\))×(1 + \(y\))= 最终量
浓度问题:
浓度 = \(\frac{ è ¨è ¨é }{ è ¨é }\)×100%
溶质质量 = 溶液质量 × 浓度
混合前溶质质量之和 = 混合后溶质质量
混合前溶液质量之和 = 混合后溶液质量
例题解析
例 1:某工厂去年的利润(总收入 - 总支出)为 200 万元,今年总收入比去年增加了 20%,总支出比去年减少了 10%,今年的利润为 780 万元,问去年的总收入、总支出各是多少万元?
解:审:已知去年利润 200 万元,今年总收入增 20%,总支出减 10%,今年利润 780 万元,求去年的总收入和总支出。
设:设去年的总收入为\(x\)万元,总支出为\(y\)万元。
找:等量关系有两个,一是 “去年总收入 - 去年总支出 = 去年利润”,二是 “今年总收入 - 今年总支出 = 今年利润”。
列:根据等量关系,列出方程组:\(\begin{cases}x - y = 200\\(1 + 20\%)x-(1 - 10\%)y = 780\end{cases}\)
化简第二个方程:\(1.2x - 0.9y = 780\)
解:由第一个方程得\(x = y + 200\) ③,把③代入第二个方程:\(
\begin{align*}
1.2(y + 200)-0.9y&=780\\
1.2y + 240 - 0.9y&=780\\
0.3y&=540\\
y&=1800
\end{align*}
\)
把\(y = 1800\)代入③得:\(x = 1800 + 200 = 2000\)。
验:去年总收入 2000 万元,总支出 1800 万元,利润\(2000 - 1800 = 200\)万元;今年总收入\(2000 1.2 = 2400\)万元,总支出\(1800 0.9 = 1620\)万元,利润\(2400 - 1620 = 780\)万元,符合题意。
答:去年的总收入是 2000 万元,总支出是 1800 万元。
例 2:有两种酒精溶液,甲种酒精溶液的浓度为 30%,乙种酒精溶液的浓度为 60%,现要配制浓度为 50% 的酒精溶液 300 克,问需要甲、乙两种酒精溶液各多少克?
解:审:甲浓度 30%,乙浓度 60%,要配浓度 50% 的溶液 300 克,求甲、乙各需多少克。
设:设需要甲种酒精溶液\(x\)克,乙种酒精溶液\(y\)克。
找:等量关系有 “甲溶液质量 + 乙溶液质量 = 混合后溶液质量” 和 “甲溶液中溶质质量 + 乙溶液中溶质质量 = 混合后溶液中溶质质量”。
列:根据等量关系,列出方程组:\(\begin{cases}x + y = 300\\30\%x + 60\%y = 50\% 300\end{cases}\)
化简第二个方程:\(0.3x + 0.6y = 150\),两边同除以 0.3 得\(x + 2y = 500\) ②
解:用② - ①得:\(y = 200\)
把\(y = 200\)代入①得:\(x = 300 - 200 = 100\)。
验:甲 100 克含溶质\(100 30\% = 30\)克,乙 200 克含溶质\(200 60\% = 120\)克,混合后溶质共 150 克,溶液 300 克,浓度\(\frac{150}{300} 100\% = 50\%\),符合题意。
答:需要甲种酒精溶液 100 克,乙种酒精溶液 200 克。
知识点:方案问题
方案问题是指根据不同的条件设计多种解决方案,通过计算和比较,选择最优方案(如成本最低、利润最高、效率最高等)。解决这类问题的关键是列出每种方案的数量关系,通过方程组求解后进行对比。
解题步骤
分析题目,确定可能的方案种类。
设出未知数,根据每种方案的条件列出方程组。
解方程组,求出每种方案的相关数据(如成本、利润等)。
比较各种方案的结果,选择最优方案。
例题解析
例 3:某中学计划购买 A、B 两种型号的课桌凳共 200 套,经调查,购买一套 A 型号课桌凳比购买一套 B 型号课桌凳少用 40 元,且购买 4 套 A 型号和 5 套 B 型号课桌凳共需 1820 元。
(1)求购买一套 A 型号、一套 B 型号的课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳的总费用不超过 40880 元,并且购买 A 型号课桌凳的数量不能超过 B 型号课桌凳数量的\(\frac{2}{3}\),求该校本次购买 A、B 两种型号课桌凳共有几种方案?哪种方案的总费用最低?
解:(1)审:A 比 B 每套少 40 元,4 套 A + 5 套 B = 1820 元,求 A、B 单价。
设:设购买一套 A 型号课桌凳需\(x\)元,一套 B 型号课桌凳需\(y\)元。
列:\(\begin{cases}y - x = 40\\4x + 5y = 1820\end{cases}\)
解:由①得\(y = x + 40\) ③,代入②得:\(
\begin{align*}
4x + 5(x + 40)&=1820\\
4x + 5x + 200&=1820\\
9x&=1620\\
x&=180
\end{align*}
\)
把\(x = 180\)代入③得\(y = 220\)。
答:购买一套 A 型号需 180 元,一套 B 型号需 220 元。
(2)审:共买 200 套,总费用≤40880 元,A 数量≤\(\frac{2}{3}\)B 数量,求方案及最低费用。
设:设购买 A 型号课桌凳\(a\)套,则购买 B 型号课桌凳\((200 - a)\)套。
列:根据条件列出不等式组:\(\begin{cases}180a + 220(200 - a) ¤40880\\a ¤\frac{2}{3}(200 - a)\end{cases}\)
解第一个不等式:\(
\begin{align*}
180a + 44000 - 220a& ¤40880\\
-40a& ¤-3120\\
a& 78
\end{align*}
\)
解第二个不等式:\(
\begin{align*}
3a& ¤2(200 - a)\\
3a& ¤400 - 2a\\
5a& ¤400\\
a& ¤80
\end{align*}
\)
所以\(78 ¤a ¤80\),因为\(a\)为整数,所以\(a = 78\)、79、80,共 3 种方案。
方案一:A78 套,B122 套,费用\(180 78 + 220 122 = 14040 + 26840 = 40880\)元;
方案二:A79 套,B121 套,费用\(180 79 + 220 121 = 14220 + 26620 = 40840\)元;
方案三:A80 套,B120 套,费用\(180 80 + 220 120 = 14400 + 26400 = 40800\)元。
比较:40800<40840<40880,方案三费用最低。
答:共有 3 种方案,购买 A 型号 80 套、B 型号 120 套的总费用最低。
例 4:某商场计划用 9 万元从生产厂家购进 50 台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为 A 种每台 1500 元,B 种每台 2100 元,C 种每台 2500 元。
(1)若商场同时购进两种不同型号的电视机共 50 台,用去 9 万元,研究一下商场的进货方案;
(2)若商场销售一台 A 种电视机可获利 150 元,销售一台 B 种电视机可获利 200 元,销售一台 C 种电视机可获利 250 元,在(1)的进货方案中,哪种方案获利最多?
解:(1)分三种情况讨论:
情况一:购进 A、B 两种型号
设购进 A 种\(x\)台,B 种\(y\)台,则\(\begin{cases}x + y = 50\\1500x + 2100y = 90000\end{cases}\)
化简第二个方程:\(5x + 7y = 300\),由①得\(x = 50 - y\),代入得:\(
\begin{align*}
5(50 - y)+7y&=300\\
250 - 5y + 7y&=300\\
2y&=50\\
y&=25
\end{align*}
\)
则\(x = 25\),即购进 A25 台,B25 台。
情况二:购进 A、C 两种型号
设购进 A 种\(m\)台,C 种\(n\)台,则\(\begin{cases}m + n = 50\\1500m + 2500n = 90000\end{cases}\)
化简第二个方程:\(3m + 5n = 180\),由①得\(m = 50 - n\),代入得:\(
\begin{align*}
3(50 - n)+5n&=180\\
150 - 3n + 5n&=180\\
2n&=30\\
n&=15
\end{align*}
\)
则\(m = 35\),即购进 A35 台,C15 台。
情况三:购进 B、C 两种型号
设购进 B 种\(p\)台,C 种\(q\)台,则\(\begin{cases}p + q = 50\\2100p + 2500q = 90000\end{cases}\)
化简第二个方程:\(21p + 25q = 900\),由①得\(p = 50 - q\),代入得:\(
\begin{align*}
21(50 - q)+25q&=900\\
1050 - 21q + 25q&=900\\
4q&=-150\\
q&=-37.5
\end{align*}
\)
台数不能为负数,此情况舍去。
答:进货方案有两种,一是购进 A25 台、B25 台;二是购进 A35 台、C15 台。
(2)计算各方案获利:
方案一获利:\(25 150 + 25 200 = 3750 + 5000 = 8750\)元;
方案二获利:\(35 150 + 15 250 = 5250 + 3750 = 9000\)元。
比较:9000>8750,方案二获利最多。
答:购进 A35 台、C15 台的方案获利最多。
小练习
某工厂第一季度生产甲、乙两种机器共 480 台,改进生产技术后,第二季度生产这两种机器共 554 台,其中甲种机器产量的增长率为 10%,乙种机器产量的增长率为 20%,问该工厂第一季度生产甲、乙两种机器各多少台?
现有含盐 20% 的盐水 500 克,要把它变成含盐 15% 的盐水,应加入含盐 5% 的盐水多少克?
某运输公司有 A、B 两种货车,3 辆 A 货车与 2 辆 B 货车一次可以运货 17 吨,5 辆 A 货车与 4 辆 B 货车一次可以运货 31 吨。
(1)求每辆 A 货车和每辆 B 货车一次分别可以运货多少吨?
(2)现有货物 32 吨,计划同时租用 A 货车和 B 货车,要求一次运完,且每辆车都装满货物,试写出所有的租车方案,并求出最少租车费(已知每辆 A 货车租车费 200 元,每辆 B 货车租车费 300 元)。
思考讨论
解决百分率问题时,如何准确找到等量关系?
解决百分率问题,首先要明确题目中涉及的是哪种类型的百分率(如增长率、浓度等),然后根据对应的基本数量关系(如 “原量 ×(1 + 增长率)= 新量”“溶质质量 = 溶液质量 × 浓度”)来构建等量关系。对于涉及两个未知量的问题,要从题目中找出两个不同的等量关系,从而列出二元一次方程组。例如在增长率问题中,通常可以从 “增长前后的数量关系” 和 “两个不同阶段的增长结果” 这两个角度寻找等量关系。
在方案问题中,如何确保不遗漏任何一种可能的方案?
在方案问题中,首先要明确题目中的限制条件(如数量范围、费用上限等),这些条件往往会确定未知数的取值范围。然后,根据未知数的实际意义(如必须为正整数),在取值范围内找出所有可能的取值,进而确定所有的方案。例如在购买物品的方案问题中,设购买 A 物品\(x\)件,B 物品\(y\)件,根据总数量和总费用的
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
百分率一般表示某部分占总体的多少,由此可以求出该部分的数量,再根据“总量 = 各部分量的和”,可以列出方程组后求解.
探索新知
例 3 玻璃厂熔炼玻璃液,原料是石英砂和长石粉混合而成,要求原料中含二氧化硅70%. 已知石英砂中含二氧化硅 99%,长石粉中含二氧化硅 67%. 在 3.2 t 原料中,石英砂和长石粉各多少?
原料成分 石英砂 长石粉 总量
质量/t x y
含二氧化硅量/t 99%x 67%y
3.2
70%×3.2
解 设原料中石英砂 x t,长石粉有 y t. 根据题意,得
x + y = 3.2,
99%x + 67%y = 70%×3.2.
解方程组,得
x = 0.3,
y = 2.9.
答:在 3.2 t 原料中,石英砂有 0.3 t,长石粉有 2.9 t.
百分比问题中常见的是增长(下降)率问题、与浓度有关的问题等,其中增长(下降)率问题中的等量关系如下:
(1)增长率 = ×100%;
增长后的量 – 增长前的量
增长前的量
(2)增长后的量 = 增长前的量×(1 + 增长率);
(3)下降率 = ×100%;
下降前的量 – 下降后的量
下降前的量
(4)下降后的量 = 下降前的量×(1 – 下降率).
巩固练习
某皮鞋厂前年的利润为 100 万元,去年的总产值比前年增加了 20% ,总支出比前年减少了 5% ,去年的利润为 400 万元,那么该皮鞋厂前年的总产值和总支出各是多少万元?
分析:设该皮鞋厂前年的总产值是 x 万元,总支出是 y 万元,
总产值/万元 总支出/万元 利润/万元
前年 x y 100
去年 (1+20%)x (1-5%)y 400
解: 设该皮鞋厂前年的总产值是 x 万元,总支出是 y 万元.
根据题意,得
x - y = 100,
(1+20%)x - (1-5%)y = 400.
解方程组,得
x = 1220,
y = 1120.
答: 该皮鞋厂前年的总产值是 1220 万元,总支出是 1120 万元.
练 习
1. 某乡今年春播作物的面积比秋播作物的面积多 630 hm2.
计划明年春播作物的面积增加 20%,秋播作物的面积减少 10%,这样明年春播、秋播作物的总面积将比今年增加 12%.这个乡今年春播与秋播作物的面积各是多少?
【教材P121 练习 第1题】
解: 设这个乡今年春播作物的面积为 x hm2,秋播作物的面积为 y hm2.
根据题意,得
x - y = 630,
x(1+20%) + y(1-10%) = (x+y)(1+12%).
解方程组,得
x = 990,
y = 360.
答: 这个乡今年春播作物的面积为 990 hm2,秋播作物的面积为 360 hm2.
2. 石岭村原有林地、旱地共 162 hm2. 村里把一部分旱地改造为林地,使旱地面积为林地面积的 20%.
求改造后的旱地面积和林地面积.
解: 设改造后的旱地面积为 x hm2,林地面积为 y hm2.
根据题意,得 解方程组,得
x + y = 162,
x = 20%y.
x = 27,
y = 135.
答: 改造后的旱地面积为 27 hm2,林地面积为 135 hm2.
【教材P121 练习 第2题】
1星题 基础练
知识点1 百分率问题
1.真实情境 某地推广智慧农业技术,将部分传统农田改造为智
能温室种植区.改造后,传统农田面积是智能温室面积的 ,
且传统农田与智能温室总面积为 .设改造后传统农田面
积为,智能温室面积为 ,则可列方程组为 ( )
B
A. B.
C. D.
2.有甲、乙两种铜和银的合金,甲种合金含银 ,乙种合
金含银,现在要熔制含银的合金 ,设需甲
合金的质量为,乙合金的质量为 ,则可列方程组为
_ _____________________________.
3.甲仓库和乙仓库共存粮450吨,现从甲仓库运出存粮的
,从乙仓库运出存粮的 ,结果乙仓库所余的粮食比
甲仓库所余的粮食多30吨.则甲仓库原来存粮_____吨,乙仓库
原来存粮_____吨.
240
210
4.(8分)某校去年有学生1 000名,今年比去年增加了 ,
其中寄宿学生增加了,走读学生减少了 ,问该校去年
有寄宿学生与走读学生各多少名?
解:设该校去年有寄宿学生名,走读学生 名.
根据题意,得
解得
答:该校去年有寄宿学生800名,走读学生200名.
知识点2 方案问题
5.[2025年1月合肥期末]已知1辆 型车载满货物一次可运
货1吨,1辆 型车载满货物一次可运货4吨.某公司有14吨货
物,计划同时租用型车和 型车,一次运完,且每辆车都
装满货物,共有租车方案( )
B
A.4种 B.3种 C.2种 D.1种
6.某校为加强爱读书、读好书、善读书的阅读氛围,准备用
720元购买图书展示架,可供选择的有 种展示架120元/个,
种展示架180元/个,在资金用尽且可以只买其中一种展示
架的情况下,一共有___种购买方案.
3
7.(8分)[2025·广州模拟]某公司组织员工去三星堆参观,现
有,两种客车可以租用.已知3辆种客车和2辆 种客车可
以坐260人,2辆种客车可坐的人数和3辆 种客车可坐的人
数一样多.
(1)请问, 两种客车每辆分别可坐多少人?
解:设种客车每辆可坐人,种客车每辆可坐 人,
根据题意,得解得
答:种客车每辆可坐60人, 种客车每辆可坐40人.
(2)已知该公司共有320名员工,请问如何安排租车方案,可
以使得所有员工恰好坐下?
设租用辆种客车,辆 种客车,根据题意,得
,所以 ,
又因为, 均为非负整数,
所以或或 所以共有3种租车方案,
方案1:租用8辆 种客车;
方案2:租用2辆种客车,5辆 种客车;
方案3:租用4辆种客车,2辆 种客车.
2星题 中档练
8.[2025年1月芜湖期末]某工程公司下属的甲工程队、乙工
程队分别承包了工程、 工程,甲工程队晴天需要14天完
成,雨天工作效率下降 ;乙工程队晴天需要15天完成,
雨天工作效率下降 ,实际上两个工程队同时开工,同时
完工,两个工程队各工作了( )
C
A.15天 B.16天 C.17天 D.18天
设两工程队各工作了天,在施工期间有 天有雨,
由题意得,
解得 故两个工程队各工作了17天.
9.(8分) 真 实 情 境[2025 合肥月考] 点点学校引入 营养
师系统,为学生定制低碳环保早餐套餐.每 早餐套餐中,
蛋白质总含量为 ,包括一个谷物面包,一盒牛奶和一个
去壳鸡蛋(一个去壳鸡蛋的质量约为 ,其中蛋白质含量为
;谷物面包和牛奶的部分主要营养成分如表所示).
项目 谷物面包(含量) 牛奶(含量)
蛋白质
脂肪
碳水化合物
设该早餐套餐中每份有谷物面包,牛奶 .
(1)请补全表格(用含有, 的代数式表示);
谷物面包 牛奶 去壳鸡蛋 总量
50 400
_______ _____ 11
(2)求出, 的值.
解:由题意,得:
解得
3星题 提升练
10.(12分)应用意识 现有若干个体积相同的
大球和体积相同的小球,根据图中的信息,
解答下面的问题:
(1)放入1个小球水面升高___,放入1个大球水面升高___ ;
2
3
(2)如果放入大球、小球共10个,要使水面
上升到 ,应放入大球、小球各多少
个
解:设应放入个大球, 个小球.
根据题意得 解得
答:应放入4个大球,6个小球.
(3)现有充足的大球和小球,要使水面上升到 ,你还有其
他方案吗
设放入个大球, 个小球,根据题意得
,所以 .又
因为,均为非负整数,所以 或
或或或
所以还有4个其他方案,分别为
方案1:放入8个大球;
方案2:放入6个大球,3个小球;
方案3:放入2个大球,9个小球;
方案4:放入12个小球.
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
