3.5.3调配、配比与配套问题 课件(共42张PPT)
文档属性
| 名称 | 3.5.3调配、配比与配套问题 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 21:03:12 | ||
图片预览







文档简介
(共42张PPT)
3.5.3调配、配比与配套问题
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
3.5.3 调配、配比与配套问题
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
前面我们学习了用二元一次方程组解决比赛得分、行程、百分率和方案等实际问题,这些问题的解决都离不开对等量关系的准确把握。今天我们将继续学习另外三类常见的实际问题 —— 调配问题、配比问题和配套问题,它们在生产、生活中应用广泛,掌握这些问题的解决方法,能进一步提升我们用数学知识解决实际问题的能力。
学习目标
理解调配问题、配比问题和配套问题的含义,掌握各自的数量关系和解题关键。
能根据这三类问题的特点,找出等量关系,列出二元一次方程组并求解。
培养分析问题和解决问题的能力,体会数学与实际生活的紧密联系。
知识点:调配问题
调配问题是指将一定数量的人员、物资等从一个地方调动到另一个地方,以满足某种需求。解决这类问题的关键是明确调配前后的数量变化,根据调配后的数量关系列出等量关系。
数量关系
调配前的数量 + 调入的数量 - 调出的数量 = 调配后的数量
调配后甲处的数量与乙处的数量满足题目给定的关系
例题解析
例 1:某车间有两个生产小组,甲组有 32 人,乙组有 28 人,现因工作需要,从甲组调出部分人到乙组,使乙组的人数是甲组人数的 2 倍,问从甲组调出多少人到乙组?
解:审:甲组原有 32 人,乙组原有 28 人,从甲组调人到乙组后,乙组人数是甲组的 2 倍,求调出人数。
设:设从甲组调出\(x\)人到乙组,调配后甲组有\(y\)人,则乙组有\(2y\)人。
找:等量关系有 “调配后甲组人数 + 调出人数 = 甲组原有人数” 和 “调配后乙组人数 - 调入人数 = 乙组原有人数”。
列:根据等量关系,列出方程组:\(\begin{cases}y + x = 32\\2y - x = 28\end{cases}\)
解:① + ②得:\(3y = 60\),解得\(y = 20\)。
把\(y = 20\)代入①得:\(20 + x = 32\),解得\(x = 12\)。
验:调出 12 人后,甲组有\(32 - 12 = 20\)人,乙组有\(28 + 12 = 40\)人,\(40\)是\(20\)的 2 倍,符合题意。
答:从甲组调出 12 人到乙组。
例 2:某学校组织学生参加社会实践活动,原计划安排 40 座的客车若干辆,但还有 20 人没有座位;如果改租 60 座的客车,则可少租 2 辆,且最后一辆车还空出 40 个座位,问原计划租 40 座的客车多少辆?参加社会实践活动的学生有多少人?
解:审:原计划租 40 座客车,有 20 人没座位;改租 60 座客车,少租 2 辆,最后一辆空 40 座,求原计划租车数量和学生人数。
设:设原计划租 40 座的客车\(x\)辆,参加社会实践活动的学生有\(y\)人。
找:等量关系有 “40 座客车可坐人数 + 20 人 = 学生总人数” 和 “60 座客车(\(x - 2\))辆可坐人数 - 40 个空座位 = 学生总人数”。
列:根据等量关系,列出方程组:\(\begin{cases}40x + 20 = y\\60(x - 2)-40 = y\end{cases}\)
解:把①代入②得:\(
\begin{align*}
60(x - 2)-40&=40x + 20\\
60x - 120 - 40&=40x + 20\\
60x - 40x&=20 + 120 + 40\\
20x&=180\\
x&=9
\end{align*}
\)
把\(x = 9\)代入①得:\(y = 40 9 + 20 = 380\)。
验:原计划租 9 辆 40 座客车,可坐\(40 9 = 360\)人,加上没座位的 20 人,共 380 人;改租\(9 - 2 = 7\)辆 60 座客车,前 6 辆坐满可坐\(60 6 = 360\)人,最后一辆坐\(380 - 360 = 20\)人,空出\(60 - 20 = 40\)个座位,符合题意。
答:原计划租 40 座的客车 9 辆,参加社会实践活动的学生有 380 人。
知识点:配比问题
配比问题是指两种或多种物质按一定的比例混合在一起,以达到某种特定的要求。解决这类问题的关键是根据题目中给出的比例关系,结合混合前后的总量不变来列出等量关系。
数量关系
各成分的数量比等于给定的比例
各成分的数量之和等于混合物的总数量
例题解析
例 3:某化工厂要配制一种浓度为 15% 的药水,现有浓度为 20% 的药水 300 克和浓度为 10% 的药水若干克,问需要浓度为 10% 的药水多少克?配制成的 15% 的药水总质量是多少克?
解:审:用 20% 的药水 300 克和 10% 的药水配制 15% 的药水,求 10% 药水的质量和配成后药水的总质量。
设:设需要浓度为 10% 的药水\(x\)克,配制成的 15% 的药水总质量是\(y\)克。
找:等量关系有 “20% 药水的质量 + 10% 药水的质量 = 配成后药水的总质量” 和 “20% 药水中溶质质量 + 10% 药水中溶质质量 = 15% 药水中溶质质量”。
列:根据等量关系,列出方程组:\(\begin{cases}300 + x = y\\20\% 300 + 10\%x = 15\%y\end{cases}\)
解:把①代入②得:\(
\begin{align*}
60 + 0.1x&=0.15(300 + x)\\
60 + 0.1x&=45 + 0.15x\\
0.15x - 0.1x&=60 - 45\\
0.05x&=15\\
x&=300
\end{align*}
\)
把\(x = 300\)代入①得:\(y = 300 + 300 = 600\)。
验:20% 的药水 300 克含溶质\(300 20\% = 60\)克,10% 的药水 300 克含溶质\(300 10\% = 30\)克,配成后药水 600 克含溶质\(60 + 30 = 90\)克,浓度为\(90 ·600 100\% = 15\%\),符合题意。
答:需要浓度为 10% 的药水 300 克,配制成的 15% 的药水总质量是 600 克。
例 4:某食品厂要配制一种什锦糖,由奶糖、水果糖和巧克力糖按\(3:5:2\)的比例混合而成。现要配制这种什锦糖 1000 千克,问需要奶糖、水果糖和巧克力糖各多少千克?
解:审:奶糖、水果糖、巧克力糖按\(3:5:2\)的比例配制 1000 千克什锦糖,求各成分的质量。
设:设需要奶糖\(3x\)千克,水果糖\(5x\)千克,巧克力糖\(2x\)千克。
找:等量关系是 “奶糖质量 + 水果糖质量 + 巧克力糖质量 = 什锦糖总质量”。
列:根据等量关系,列出方程:\(3x + 5x + 2x = 1000\)
解:\(10x = 1000\),解得\(x = 100\)。
则奶糖质量为\(3x = 3 100 = 300\)千克,水果糖质量为\(5x = 5 100 = 500\)千克,巧克力糖质量为\(2x = 2 100 = 200\)千克。
验:\(300 + 500 + 200 = 1000\)千克,且\(300:500:200 = 3:5:2\),符合题意。
答:需要奶糖 300 千克,水果糖 500 千克,巧克力糖 200 千克。
知识点:配套问题
配套问题是指在生产过程中,不同的零件或产品之间按照一定的比例进行搭配,以形成一个完整的产品。解决这类问题的关键是明确配套的比例关系,根据比例列出等量关系。
数量关系
若\(a\)个甲零件和\(b\)个乙零件配成一套,则甲零件的数量 ×\(b\) = 乙零件的数量 ×\(a\)
例题解析
例 5:某车间有 22 名工人,每人每天可以生产 1200 个螺钉或 2000 个螺母。1 个螺钉需要配 2 个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
解:审:车间有 22 名工人,每人每天生产 1200 个螺钉或 2000 个螺母,1 个螺钉配 2 个螺母,求生产螺钉和螺母的工人数。
设:设应安排\(x\)名工人生产螺钉,\(y\)名工人生产螺母。
找:等量关系有 “生产螺钉的工人数 + 生产螺母的工人数 = 总人数” 和 “每天生产的螺母数量 = 2× 每天生产的螺钉数量”。
列:根据等量关系,列出方程组:\(\begin{cases}x + y = 22\\2000y = 2 1200x\end{cases}\)
化简第二个方程得:\(2000y = 2400x\),即\(5y = 6x\) ③
解:由①得\(x = 22 - y\) ④,把④代入③得:\(
\begin{align*}
5y&=6(22 - y)\\
5y&=132 - 6y\\
5y + 6y&=132\\
11y&=132\\
y&=12
\end{align*}
\)
把\(y = 12\)代入④得:\(x = 22 - 12 = 10\)。
验:10 名工人生产螺钉,每天生产\(10 1200 = 12000\)个;12 名工人生产螺母,每天生产\(12 2000 = 24000\)个,\(24000 = 2 12000\),刚好配套,符合题意。
答:应安排 10 名工人生产螺钉,12 名工人生产螺母。
例 6:某服装厂有工人 54 人,每人每天可加工上衣 8 件或裤子 10 条,应怎样分配人数,才能使每天生产的上衣和裤子配套?(1 件上衣配 1 条裤子)
解:审:服装厂有 54 名工人,每人每天加工上衣 8 件或裤子 10 条,1 件上衣配 1 条裤子,求加工上衣和裤子的工人数。
设:设分配\(x\)人加工上衣,\(y\)人加工裤子。
找:等量关系有 “加工上衣的人数 + 加工裤子的人数 = 总人数” 和 “每天生产的上衣数量 = 每天生产的裤子数量”。
列:根据等量关系,列出方程组:\(\begin{cases}x + y = 54\\8x = 10y\end{cases}\)
化简第二个方程得:\(4x = 5y\),即\(x=\frac{5}{4}y\) ③
解:把③代入①得:\(
\begin{align*}
\frac{5}{4}y + y&=54\\
\frac{5}{4}y+\frac{4}{4}y&=54\\
\frac{9}{4}y&=54\\
y&=54 \frac{4}{9}\\
y&=24
\end{align*}
\)
把\(y = 24\)代入③得:\(x=\frac{5}{4} 24 = 30\)。
验:30 人加工上衣,每天生产\(30 8 = 240\)件;24 人加工裤子,每天生产\(24 10 = 240\)条,上衣和裤子数量相等,刚好配套,符合题意。
答:应分配 30 人加工上衣,24 人加工裤子。
小练习
某学校组织学生参加植树活动,原计划安排 45 名学生去植树,每人植树 6 棵,由于特殊情况,有部分学生不能参加,实际参加的学生人数是原计划的\(\frac{4}{5}\),实际每人植树多少棵?
要配制一种盐水,盐和水的质量比是\(1:10\),现有盐 20 克,需要加水多少克?配制成的盐水总质量是多少克?
某车间有工人 85 人,平均每人每天可加工大齿轮 16 个或小齿轮 10 个,2 个大齿轮和 3 个小齿轮配成一套,问应如何安排工人加工大、小齿轮,才能使每天加工的大、小齿轮刚好配套?
思考讨论
调配问题和配比问题有什么异同点?
相同点:都涉及到数量的调整和组合,都需要根据题目中的条件找出等量关系来列方程(组)求解。
不同点:调配问题主要是对人员、物资等进行调动,重点关注调配前后数量的变化以及调配后各部分数量之间的关系;配比问题则是将不同的物质按一定比例混合,重点关注混合前后各成分的数量以及它们之间的比例关系。
解决配套问题时,如何准确确定配套的比例关系?
解决配套问题,首先要明确一个完整的配套产品中各零件或部件的数量关系,例如 “1 个 A 配 2 个 B”“3 个 C 和 4 个 D 配成一套” 等,然后根据这个数量关系列出 “甲零件数量 × 乙零件的配套数 = 乙零件数量 × 甲零件的配套数” 这样的等量关系。在分析过程中,要仔细阅读题目,确保对配套比例的理解准确无误。
课堂小结
调配问题:关键是理清调配前后的数量变化,根据调配后各部分的数量关系列出等量关系,设出调配的数量和调配后各部分的数量,列出方程组求解。
配比问题:要根据题目中给出的比例关系,结合混合前后各成分的总量不变以及溶质(或其他成分)的总量不变来确定等量关系,进而列出方程组。
配套问题:核心是明确配套的比例,根据 “甲零件数量 × 乙的配套数 = 乙零件数量 × 甲的配套数” 这一关键等量关系,结合总人数或总工作量等条件列出方程组。
通过本节课的学习,我们进一步掌握了用二元一次方程组解决实际问题的方法,在解决这些问题时,要仔细审题,准确找出等量关系,合理设未知数,确保解题的正确性。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
探索新知
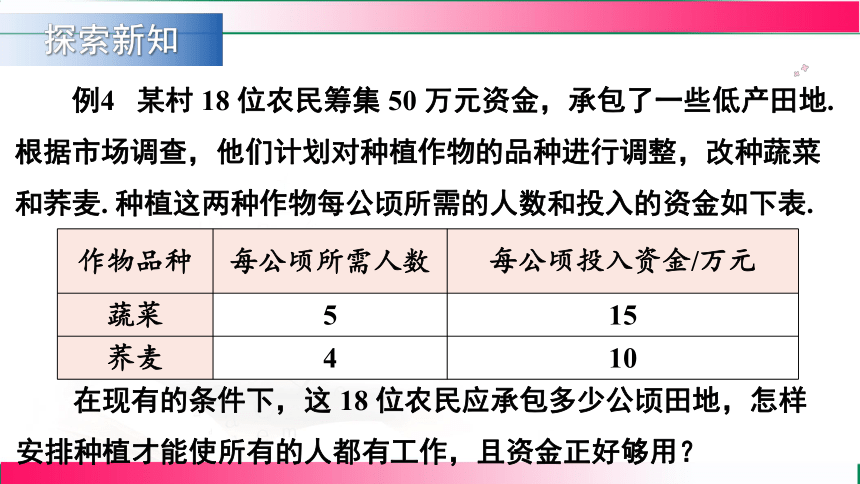
例4 某村 18 位农民筹集 50 万元资金,承包了一些低产田地. 根据市场调查,他们计划对种植作物的品种进行调整,改种蔬菜和荞麦. 种植这两种作物每公顷所需的人数和投入的资金如下表.
作物品种 每公顷所需人数 每公顷投入资金/万元
蔬菜 5 15
荞麦 4 10
在现有的条件下,这 18 位农民应承包多少公顷田地,怎样安排种植才能使所有的人都有工作,且资金正好够用?
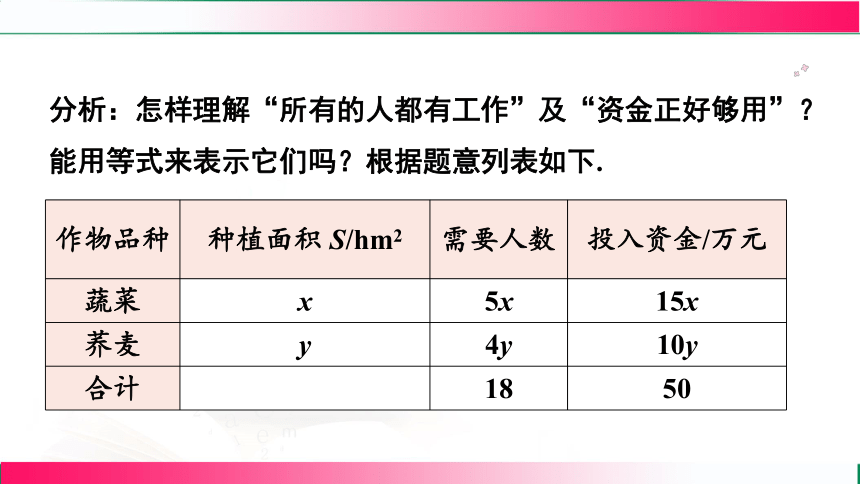
分析:怎样理解“所有的人都有工作”及“资金正好够用”?能用等式来表示它们吗?根据题意列表如下.
作物品种 种植面积 S/hm2 需要人数 投入资金/万元
蔬菜 x 5x 15x
荞麦 y 4y 10y
合计 18 50
解 设蔬菜的种植面积为 x hm2,荞麦的种植面积为 y hm2. 根据题意,得
5x + 4y = 18,
15x + 10y = 50.
解方程组,得
x = 2,
y = 2.
答:这 18 位农民应承包 4 hm2 的田地,种植蔬菜和荞麦各 2 hm2,并安排 10 人种蔬菜,8 人种荞麦,这样能使所有的人都有工作,且资金正好够用.
则 x + y = 4. 此时 5x = 5×2 = 10,4y = 4×2 = 8.
表格能够将复杂的数量关系明朗化,而且更容易分析出等量关系.
知识点睛
巩固练习
1. 星期天,七年级(1)(2)两班部分同学相约去某公园玩碰碰车或划船. 已知玩碰碰车的同学每人租用一辆车,划船的同学每 4 人合租一条船,两班各花了115 元. 活动人数如下表:
碰碰车每辆车租金多少元?游船每条船租金多少元?
班级 玩碰碰车的同学 划船的同学
(1)班 11 人 16 人
(2)班 8 人 20 人
分析:
班级 租碰碰车的数量 租船的数量 租金
(1)班 11 4 115
(2)班 8 5 115
解: 设碰碰车每辆车租金 x 元,游船每条船租金 y 元.
则
解得
x = 5,
y = 15.
解: 碰碰车每辆车租金 5 元,游船每条船租金 15 元.
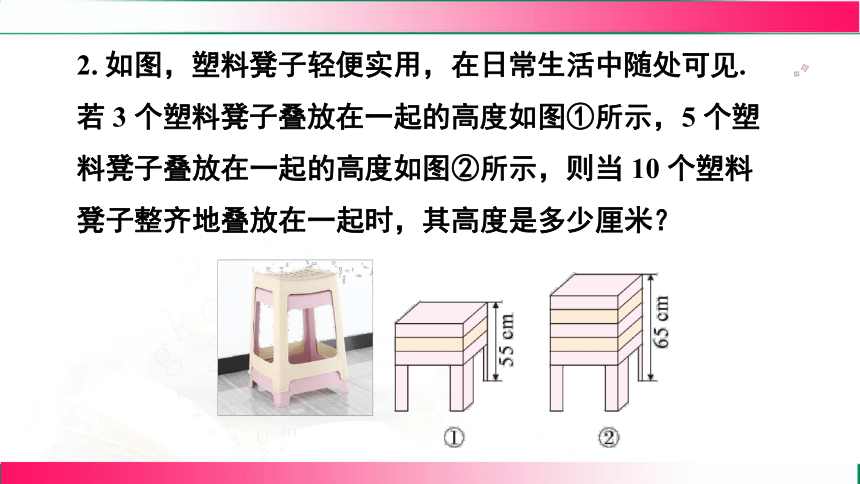
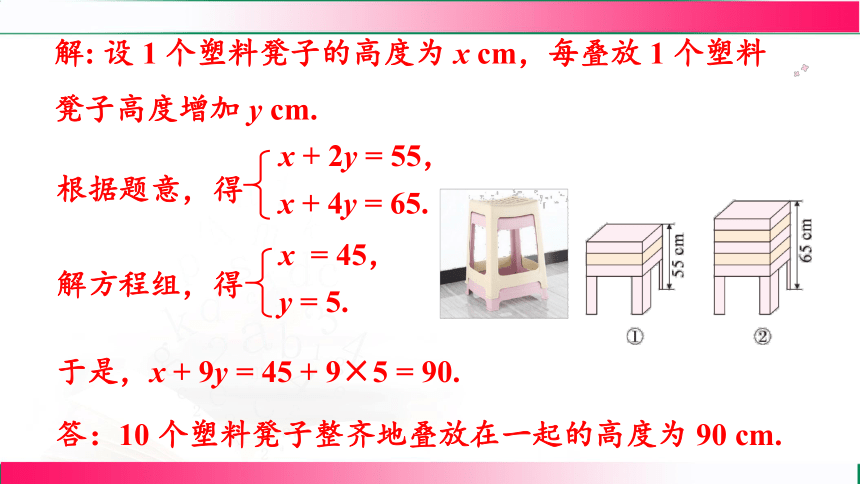
2. 如图,塑料凳子轻便实用,在日常生活中随处可见. 若 3 个塑料凳子叠放在一起的高度如图①所示,5 个塑料凳子叠放在一起的高度如图②所示,则当 10 个塑料凳子整齐地叠放在一起时,其高度是多少厘米?
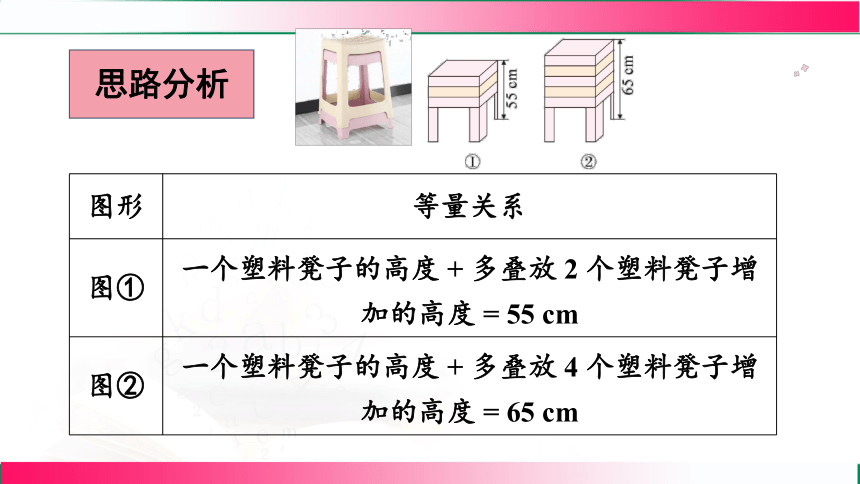
思路分析
图形 等量关系
图① 一个塑料凳子的高度 + 多叠放 2 个塑料凳子增加的高度 = 55 cm
图② 一个塑料凳子的高度 + 多叠放 4 个塑料凳子增加的高度 = 65 cm
解: 设 1 个塑料凳子的高度为 x cm,每叠放 1 个塑料凳子高度增加 y cm.
根据题意,得
x + 2y = 55,
x + 4y = 65.
解方程组,得
x = 45,
y = 5.
于是,x + 9y = 45 + 9×5 = 90.
答:10 个塑料凳子整齐地叠放在一起的高度为 90 cm.
3. 某电视机厂生产甲、乙、丙三种不同型号的电视机,每台出厂价分别为 1 200 元、2 000 元、2 200元. 某商场同时从该厂购进其中两种不同型号的电视机共 50 台,正好用去 80 000 元.
(1)该商场有几种进货方案?(写出演算步骤)
(2)若该商场销售甲、乙、丙三种电视机每台可分别获得 200 元、250 元、300 元,如何进货可使售完后获利最大? 最大利润是多少?
思路分析
解:(1)设甲、乙、丙三种电视机分别购进 x 台、y 台、z 台.
根据题意,得
x + y = 50,
1200x + 2000y = 80000.
解方程组,得
x = 25,
y = 25.
①若购进甲、乙两种型号的电视机,
根据题意,得
x + z = 50,
1200x + 2200z = 80000.
解方程组,得
x = 30,
z = 20.
②若购进甲、丙两种型号的电视机,
根据题意,得
y + z = 50,
2000y + 2200z = 80000.
解方程组,得
y = 150,
z = -100.
③若购进乙、丙两种型号的电视机,
(不合题意,舍去)
故该商场有两种进货方案:
①购进 25 台甲种电视机和 25 台乙种电视机;
②购进 30 台甲种电视机和 20 台丙种电视机.
(2)方案①的利润为 200×25 + 250×25 =11250(元),
方案②的利润为 200×30+300×20 =12000(元).
因为 12000 > 11250,所以购进 30 台甲种电视机和 20 台
丙种电视机可使售完后获利最大,最大利润为 12000 元.
练 习
1. 某医院利用甲、乙两种原料为患者配制营养品. 已知每克甲原料含 0.6 单位蛋白质和 0.08 单位铁质,每克乙原料含 0.5 单位蛋白质和 0.04 单位铁质,如果患者每餐需 34 单位蛋白质和 4 单位铁质,那么每餐甲、乙两种原料各多少克恰好满足患者的需要?
【教材P122 练习 第1题】
解: 设每餐需要甲种原料 x g,乙种原料 y g.
根据题意,得
0.6x + 0.5y = 34,
0.08x + 0.04y = 4.
解方程组,得
x = 40,
y = 20.
答:每餐需要甲种原料 40 g,乙种原料 20 g 恰好满足患者的需要.
2. 向某地运送物资. 第一批 480 t,用 8 节火车车厢和20 辆卡车正好装完. 第二批 540 t,用 10 节火车车厢和 5 辆卡车正好装完,求每节火车车厢和每辆卡车分别能装多少吨.
【教材P122 练习 第2题】
解: 设每节火车车厢能装 x t,每辆卡车能装 y t.
根据题意,得
8x + 20y = 480,
10x + 5y = 540.
解方程组,得
x = 52.5,
y = 3.
解: 每节火车车厢能装 52.5 t,每辆卡车能装 3 t.
1星题 基础练
知识点1 调配问题
1.学校组织植树活动,已知在甲处植树的有23人,在乙处植树
的有17人,现调20人去支援,使在甲处植树的人数是乙处植
树人数的2倍.设调往甲处人,调往乙处 人,则可列方程组
为( )
B
A. B.
C. D.
2.(8分)[2025·滁州月考]甲、乙两车间各有工人若干名,若
从甲车间调100人给乙车间,则甲车间人数是乙车间人数的 ,
若从乙车间调100人给甲车间,则甲车间人数与乙车间人数
相同.甲、乙两车间分别原有多少名工人
解:设甲车间原有名工人,乙车间原有 名工人,
根据题意,得解得
答:甲车间原有180名工人,乙车间原有380名工人.
知识点2 配比问题
3.(8分)跨学科·化学 为了使某植物的长势更好,张叔叔决定
利用甲、乙两种肥料配制营养肥料.已知每克甲种肥料中含有
0.6单位镁元素和0.08单位铁元素,每克乙种肥料中含有0.5单
位镁元素和0.04单位铁元素.如果每次施肥需要34单位镁元素
和4单位铁元素,那么每次施肥需要甲、乙两种肥料各多少
克才能使该植物长势更好?
解:设每次施肥需要甲种肥料克、乙种肥料 克,根据题意
得解得
答:每次施肥需要甲种肥料40克、乙种肥料20克.
知识点3 配套问题
主图情境
生产中的数学智慧
工业生产如精密齿轮,各环节紧密配合,从工人的分工
协作到零件的配套生产,每一处都闪烁着数学智慧的光芒.
4.[2025年1月芜湖期末]在一家专注光学产品制造的车间里,
60名工人投入太阳镜的生产,1名工人每天可生产镜片200片或
镜架50个.每副太阳镜由2片镜片和1个镜架配成一套,应如何分
配工人生产镜片和镜架,才能使产品正好配套?设安排 名工
人生产镜片, 名工人生产镜架,则可列方程组为 ( )
D
A. B.
C. D.
5.某机械厂加工车间有85名工人,平均每人每天加工大齿轮16
个或小齿轮10个.已知2个大齿轮与3个小齿轮配成一套,安排
____名工人加工大齿轮,才能使每天加工的大小齿轮刚好配套.
25
6.(8分)某工厂计划生产一种新型豆浆机,每台豆浆机需3个 零
件和5个零件.已知车间每天能生产零件450个或 零件300
个.现在要求在21天中所生产的零件刚好配套,那么应安排多
少天生产零件,多少天生产 零件 这些零件可以满足生产多
少台豆浆机
解:设应安排天生产零件,天生产 零件.根据题意,得
解得
(个), (台).
答:应安排6天生产零件,15天生产 零件,这些零件可以
满足生产900台豆浆机.
2星题 中档练
7.[2025年1月大同期末]为提高病人免疫力,某医院精选甲、
乙两种食物为病人配制营养餐.已知每克甲种食物中铁的含量
是蛋白质的2倍,每克乙种食物中铁的含量是蛋白质的 .如果
病人每餐需要175个单位的蛋白质和200个单位的铁,每餐需
要甲、乙两种食物分别为140克、150克,则每克甲种食物中
含铁___个单位.
1
设每克甲种食物中含蛋白质 个单位,每克乙种食物
中含蛋白质 个单位.根据题意,得
解得
所以 ,所以每克甲种食物中含铁1个单位.
8.(12分)真实情境 为助力“零碳乡村”建设,某科技公司使用
新能源货车和智能物流无人机向乡村配送190套太阳能发电
设备,已知货车每辆可运送设备20套,无人机每架可运送设
备30套,货车和无人机一共用了8辆满载运送.
(1)小宇同学根据题意列出了一个尚不完整的方程组
请写出小宇所列方程组中未知数, 表示的
意义:表示________________, 表示__________________,
该方程组中“?”处的数应是___,“*”处的数应是_____;
使用货车的数量
使用无人机的数量
8
190
(2)小琼同学的思路是设货车运送套设备,无人机运送 套
设备.请你按照小琼的思路列出方程组,并求使用货车的数量;
解:依题意得解得
所以 .
答:使用货车5辆.
(3)如果每辆货车的运费是180元,每架无人机的运费是300元,
那么该公司运送这190套设备后的总运费是多少?
总运费为 (元).
答:该公司运送这190套设备后的总运费是1 800元.
9.(8分)[2025年1月合肥期末]某工厂生
产如图①所示的长方形和正方形纸板,
做成如图②所示的竖式与横式两种长方
体形状的无盖纸盒,其中竖式纸盒由4个长方形和1个正方形
纸板做成,横式纸盒由3个长方形和2个正方形纸板做成
(给定的长方形和正方形纸板都不用裁剪,也不考虑接缝).
(1)现有长方形纸板340个,正方形纸板
160个,做成上述两种纸盒,纸板恰好用
完,求两种纸盒的生产个数.
解:设做成的竖式纸盒有个,横式纸盒有 个,根据题意得
解得
答:做成的竖式纸盒有40个,横式纸盒有60个.
(2)纸板车间共有78名工人,每名工人一
天能生产70个长方形纸板或者100个正方
形纸板.已知一个竖式纸盒与一个横式纸
盒配套,要求纸板车间一天生产的纸板由其他车间做成的竖
式纸盒与横式纸盒配套,问纸板车间应如何安排工人生产这
两种纸板?
设分配名工人生产正方形纸板, 名工
人生产长方形纸板,由题意,
得解得
答:纸板车间应分配18名工人生产正方
形纸板,60名工人生产长方形纸板.
谢谢观看!
3.5.3调配、配比与配套问题
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
3.5.3 调配、配比与配套问题
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
前面我们学习了用二元一次方程组解决比赛得分、行程、百分率和方案等实际问题,这些问题的解决都离不开对等量关系的准确把握。今天我们将继续学习另外三类常见的实际问题 —— 调配问题、配比问题和配套问题,它们在生产、生活中应用广泛,掌握这些问题的解决方法,能进一步提升我们用数学知识解决实际问题的能力。
学习目标
理解调配问题、配比问题和配套问题的含义,掌握各自的数量关系和解题关键。
能根据这三类问题的特点,找出等量关系,列出二元一次方程组并求解。
培养分析问题和解决问题的能力,体会数学与实际生活的紧密联系。
知识点:调配问题
调配问题是指将一定数量的人员、物资等从一个地方调动到另一个地方,以满足某种需求。解决这类问题的关键是明确调配前后的数量变化,根据调配后的数量关系列出等量关系。
数量关系
调配前的数量 + 调入的数量 - 调出的数量 = 调配后的数量
调配后甲处的数量与乙处的数量满足题目给定的关系
例题解析
例 1:某车间有两个生产小组,甲组有 32 人,乙组有 28 人,现因工作需要,从甲组调出部分人到乙组,使乙组的人数是甲组人数的 2 倍,问从甲组调出多少人到乙组?
解:审:甲组原有 32 人,乙组原有 28 人,从甲组调人到乙组后,乙组人数是甲组的 2 倍,求调出人数。
设:设从甲组调出\(x\)人到乙组,调配后甲组有\(y\)人,则乙组有\(2y\)人。
找:等量关系有 “调配后甲组人数 + 调出人数 = 甲组原有人数” 和 “调配后乙组人数 - 调入人数 = 乙组原有人数”。
列:根据等量关系,列出方程组:\(\begin{cases}y + x = 32\\2y - x = 28\end{cases}\)
解:① + ②得:\(3y = 60\),解得\(y = 20\)。
把\(y = 20\)代入①得:\(20 + x = 32\),解得\(x = 12\)。
验:调出 12 人后,甲组有\(32 - 12 = 20\)人,乙组有\(28 + 12 = 40\)人,\(40\)是\(20\)的 2 倍,符合题意。
答:从甲组调出 12 人到乙组。
例 2:某学校组织学生参加社会实践活动,原计划安排 40 座的客车若干辆,但还有 20 人没有座位;如果改租 60 座的客车,则可少租 2 辆,且最后一辆车还空出 40 个座位,问原计划租 40 座的客车多少辆?参加社会实践活动的学生有多少人?
解:审:原计划租 40 座客车,有 20 人没座位;改租 60 座客车,少租 2 辆,最后一辆空 40 座,求原计划租车数量和学生人数。
设:设原计划租 40 座的客车\(x\)辆,参加社会实践活动的学生有\(y\)人。
找:等量关系有 “40 座客车可坐人数 + 20 人 = 学生总人数” 和 “60 座客车(\(x - 2\))辆可坐人数 - 40 个空座位 = 学生总人数”。
列:根据等量关系,列出方程组:\(\begin{cases}40x + 20 = y\\60(x - 2)-40 = y\end{cases}\)
解:把①代入②得:\(
\begin{align*}
60(x - 2)-40&=40x + 20\\
60x - 120 - 40&=40x + 20\\
60x - 40x&=20 + 120 + 40\\
20x&=180\\
x&=9
\end{align*}
\)
把\(x = 9\)代入①得:\(y = 40 9 + 20 = 380\)。
验:原计划租 9 辆 40 座客车,可坐\(40 9 = 360\)人,加上没座位的 20 人,共 380 人;改租\(9 - 2 = 7\)辆 60 座客车,前 6 辆坐满可坐\(60 6 = 360\)人,最后一辆坐\(380 - 360 = 20\)人,空出\(60 - 20 = 40\)个座位,符合题意。
答:原计划租 40 座的客车 9 辆,参加社会实践活动的学生有 380 人。
知识点:配比问题
配比问题是指两种或多种物质按一定的比例混合在一起,以达到某种特定的要求。解决这类问题的关键是根据题目中给出的比例关系,结合混合前后的总量不变来列出等量关系。
数量关系
各成分的数量比等于给定的比例
各成分的数量之和等于混合物的总数量
例题解析
例 3:某化工厂要配制一种浓度为 15% 的药水,现有浓度为 20% 的药水 300 克和浓度为 10% 的药水若干克,问需要浓度为 10% 的药水多少克?配制成的 15% 的药水总质量是多少克?
解:审:用 20% 的药水 300 克和 10% 的药水配制 15% 的药水,求 10% 药水的质量和配成后药水的总质量。
设:设需要浓度为 10% 的药水\(x\)克,配制成的 15% 的药水总质量是\(y\)克。
找:等量关系有 “20% 药水的质量 + 10% 药水的质量 = 配成后药水的总质量” 和 “20% 药水中溶质质量 + 10% 药水中溶质质量 = 15% 药水中溶质质量”。
列:根据等量关系,列出方程组:\(\begin{cases}300 + x = y\\20\% 300 + 10\%x = 15\%y\end{cases}\)
解:把①代入②得:\(
\begin{align*}
60 + 0.1x&=0.15(300 + x)\\
60 + 0.1x&=45 + 0.15x\\
0.15x - 0.1x&=60 - 45\\
0.05x&=15\\
x&=300
\end{align*}
\)
把\(x = 300\)代入①得:\(y = 300 + 300 = 600\)。
验:20% 的药水 300 克含溶质\(300 20\% = 60\)克,10% 的药水 300 克含溶质\(300 10\% = 30\)克,配成后药水 600 克含溶质\(60 + 30 = 90\)克,浓度为\(90 ·600 100\% = 15\%\),符合题意。
答:需要浓度为 10% 的药水 300 克,配制成的 15% 的药水总质量是 600 克。
例 4:某食品厂要配制一种什锦糖,由奶糖、水果糖和巧克力糖按\(3:5:2\)的比例混合而成。现要配制这种什锦糖 1000 千克,问需要奶糖、水果糖和巧克力糖各多少千克?
解:审:奶糖、水果糖、巧克力糖按\(3:5:2\)的比例配制 1000 千克什锦糖,求各成分的质量。
设:设需要奶糖\(3x\)千克,水果糖\(5x\)千克,巧克力糖\(2x\)千克。
找:等量关系是 “奶糖质量 + 水果糖质量 + 巧克力糖质量 = 什锦糖总质量”。
列:根据等量关系,列出方程:\(3x + 5x + 2x = 1000\)
解:\(10x = 1000\),解得\(x = 100\)。
则奶糖质量为\(3x = 3 100 = 300\)千克,水果糖质量为\(5x = 5 100 = 500\)千克,巧克力糖质量为\(2x = 2 100 = 200\)千克。
验:\(300 + 500 + 200 = 1000\)千克,且\(300:500:200 = 3:5:2\),符合题意。
答:需要奶糖 300 千克,水果糖 500 千克,巧克力糖 200 千克。
知识点:配套问题
配套问题是指在生产过程中,不同的零件或产品之间按照一定的比例进行搭配,以形成一个完整的产品。解决这类问题的关键是明确配套的比例关系,根据比例列出等量关系。
数量关系
若\(a\)个甲零件和\(b\)个乙零件配成一套,则甲零件的数量 ×\(b\) = 乙零件的数量 ×\(a\)
例题解析
例 5:某车间有 22 名工人,每人每天可以生产 1200 个螺钉或 2000 个螺母。1 个螺钉需要配 2 个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
解:审:车间有 22 名工人,每人每天生产 1200 个螺钉或 2000 个螺母,1 个螺钉配 2 个螺母,求生产螺钉和螺母的工人数。
设:设应安排\(x\)名工人生产螺钉,\(y\)名工人生产螺母。
找:等量关系有 “生产螺钉的工人数 + 生产螺母的工人数 = 总人数” 和 “每天生产的螺母数量 = 2× 每天生产的螺钉数量”。
列:根据等量关系,列出方程组:\(\begin{cases}x + y = 22\\2000y = 2 1200x\end{cases}\)
化简第二个方程得:\(2000y = 2400x\),即\(5y = 6x\) ③
解:由①得\(x = 22 - y\) ④,把④代入③得:\(
\begin{align*}
5y&=6(22 - y)\\
5y&=132 - 6y\\
5y + 6y&=132\\
11y&=132\\
y&=12
\end{align*}
\)
把\(y = 12\)代入④得:\(x = 22 - 12 = 10\)。
验:10 名工人生产螺钉,每天生产\(10 1200 = 12000\)个;12 名工人生产螺母,每天生产\(12 2000 = 24000\)个,\(24000 = 2 12000\),刚好配套,符合题意。
答:应安排 10 名工人生产螺钉,12 名工人生产螺母。
例 6:某服装厂有工人 54 人,每人每天可加工上衣 8 件或裤子 10 条,应怎样分配人数,才能使每天生产的上衣和裤子配套?(1 件上衣配 1 条裤子)
解:审:服装厂有 54 名工人,每人每天加工上衣 8 件或裤子 10 条,1 件上衣配 1 条裤子,求加工上衣和裤子的工人数。
设:设分配\(x\)人加工上衣,\(y\)人加工裤子。
找:等量关系有 “加工上衣的人数 + 加工裤子的人数 = 总人数” 和 “每天生产的上衣数量 = 每天生产的裤子数量”。
列:根据等量关系,列出方程组:\(\begin{cases}x + y = 54\\8x = 10y\end{cases}\)
化简第二个方程得:\(4x = 5y\),即\(x=\frac{5}{4}y\) ③
解:把③代入①得:\(
\begin{align*}
\frac{5}{4}y + y&=54\\
\frac{5}{4}y+\frac{4}{4}y&=54\\
\frac{9}{4}y&=54\\
y&=54 \frac{4}{9}\\
y&=24
\end{align*}
\)
把\(y = 24\)代入③得:\(x=\frac{5}{4} 24 = 30\)。
验:30 人加工上衣,每天生产\(30 8 = 240\)件;24 人加工裤子,每天生产\(24 10 = 240\)条,上衣和裤子数量相等,刚好配套,符合题意。
答:应分配 30 人加工上衣,24 人加工裤子。
小练习
某学校组织学生参加植树活动,原计划安排 45 名学生去植树,每人植树 6 棵,由于特殊情况,有部分学生不能参加,实际参加的学生人数是原计划的\(\frac{4}{5}\),实际每人植树多少棵?
要配制一种盐水,盐和水的质量比是\(1:10\),现有盐 20 克,需要加水多少克?配制成的盐水总质量是多少克?
某车间有工人 85 人,平均每人每天可加工大齿轮 16 个或小齿轮 10 个,2 个大齿轮和 3 个小齿轮配成一套,问应如何安排工人加工大、小齿轮,才能使每天加工的大、小齿轮刚好配套?
思考讨论
调配问题和配比问题有什么异同点?
相同点:都涉及到数量的调整和组合,都需要根据题目中的条件找出等量关系来列方程(组)求解。
不同点:调配问题主要是对人员、物资等进行调动,重点关注调配前后数量的变化以及调配后各部分数量之间的关系;配比问题则是将不同的物质按一定比例混合,重点关注混合前后各成分的数量以及它们之间的比例关系。
解决配套问题时,如何准确确定配套的比例关系?
解决配套问题,首先要明确一个完整的配套产品中各零件或部件的数量关系,例如 “1 个 A 配 2 个 B”“3 个 C 和 4 个 D 配成一套” 等,然后根据这个数量关系列出 “甲零件数量 × 乙零件的配套数 = 乙零件数量 × 甲零件的配套数” 这样的等量关系。在分析过程中,要仔细阅读题目,确保对配套比例的理解准确无误。
课堂小结
调配问题:关键是理清调配前后的数量变化,根据调配后各部分的数量关系列出等量关系,设出调配的数量和调配后各部分的数量,列出方程组求解。
配比问题:要根据题目中给出的比例关系,结合混合前后各成分的总量不变以及溶质(或其他成分)的总量不变来确定等量关系,进而列出方程组。
配套问题:核心是明确配套的比例,根据 “甲零件数量 × 乙的配套数 = 乙零件数量 × 甲的配套数” 这一关键等量关系,结合总人数或总工作量等条件列出方程组。
通过本节课的学习,我们进一步掌握了用二元一次方程组解决实际问题的方法,在解决这些问题时,要仔细审题,准确找出等量关系,合理设未知数,确保解题的正确性。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
探索新知
例4 某村 18 位农民筹集 50 万元资金,承包了一些低产田地. 根据市场调查,他们计划对种植作物的品种进行调整,改种蔬菜和荞麦. 种植这两种作物每公顷所需的人数和投入的资金如下表.
作物品种 每公顷所需人数 每公顷投入资金/万元
蔬菜 5 15
荞麦 4 10
在现有的条件下,这 18 位农民应承包多少公顷田地,怎样安排种植才能使所有的人都有工作,且资金正好够用?
分析:怎样理解“所有的人都有工作”及“资金正好够用”?能用等式来表示它们吗?根据题意列表如下.
作物品种 种植面积 S/hm2 需要人数 投入资金/万元
蔬菜 x 5x 15x
荞麦 y 4y 10y
合计 18 50
解 设蔬菜的种植面积为 x hm2,荞麦的种植面积为 y hm2. 根据题意,得
5x + 4y = 18,
15x + 10y = 50.
解方程组,得
x = 2,
y = 2.
答:这 18 位农民应承包 4 hm2 的田地,种植蔬菜和荞麦各 2 hm2,并安排 10 人种蔬菜,8 人种荞麦,这样能使所有的人都有工作,且资金正好够用.
则 x + y = 4. 此时 5x = 5×2 = 10,4y = 4×2 = 8.
表格能够将复杂的数量关系明朗化,而且更容易分析出等量关系.
知识点睛
巩固练习
1. 星期天,七年级(1)(2)两班部分同学相约去某公园玩碰碰车或划船. 已知玩碰碰车的同学每人租用一辆车,划船的同学每 4 人合租一条船,两班各花了115 元. 活动人数如下表:
碰碰车每辆车租金多少元?游船每条船租金多少元?
班级 玩碰碰车的同学 划船的同学
(1)班 11 人 16 人
(2)班 8 人 20 人
分析:
班级 租碰碰车的数量 租船的数量 租金
(1)班 11 4 115
(2)班 8 5 115
解: 设碰碰车每辆车租金 x 元,游船每条船租金 y 元.
则
解得
x = 5,
y = 15.
解: 碰碰车每辆车租金 5 元,游船每条船租金 15 元.
2. 如图,塑料凳子轻便实用,在日常生活中随处可见. 若 3 个塑料凳子叠放在一起的高度如图①所示,5 个塑料凳子叠放在一起的高度如图②所示,则当 10 个塑料凳子整齐地叠放在一起时,其高度是多少厘米?
思路分析
图形 等量关系
图① 一个塑料凳子的高度 + 多叠放 2 个塑料凳子增加的高度 = 55 cm
图② 一个塑料凳子的高度 + 多叠放 4 个塑料凳子增加的高度 = 65 cm
解: 设 1 个塑料凳子的高度为 x cm,每叠放 1 个塑料凳子高度增加 y cm.
根据题意,得
x + 2y = 55,
x + 4y = 65.
解方程组,得
x = 45,
y = 5.
于是,x + 9y = 45 + 9×5 = 90.
答:10 个塑料凳子整齐地叠放在一起的高度为 90 cm.
3. 某电视机厂生产甲、乙、丙三种不同型号的电视机,每台出厂价分别为 1 200 元、2 000 元、2 200元. 某商场同时从该厂购进其中两种不同型号的电视机共 50 台,正好用去 80 000 元.
(1)该商场有几种进货方案?(写出演算步骤)
(2)若该商场销售甲、乙、丙三种电视机每台可分别获得 200 元、250 元、300 元,如何进货可使售完后获利最大? 最大利润是多少?
思路分析
解:(1)设甲、乙、丙三种电视机分别购进 x 台、y 台、z 台.
根据题意,得
x + y = 50,
1200x + 2000y = 80000.
解方程组,得
x = 25,
y = 25.
①若购进甲、乙两种型号的电视机,
根据题意,得
x + z = 50,
1200x + 2200z = 80000.
解方程组,得
x = 30,
z = 20.
②若购进甲、丙两种型号的电视机,
根据题意,得
y + z = 50,
2000y + 2200z = 80000.
解方程组,得
y = 150,
z = -100.
③若购进乙、丙两种型号的电视机,
(不合题意,舍去)
故该商场有两种进货方案:
①购进 25 台甲种电视机和 25 台乙种电视机;
②购进 30 台甲种电视机和 20 台丙种电视机.
(2)方案①的利润为 200×25 + 250×25 =11250(元),
方案②的利润为 200×30+300×20 =12000(元).
因为 12000 > 11250,所以购进 30 台甲种电视机和 20 台
丙种电视机可使售完后获利最大,最大利润为 12000 元.
练 习
1. 某医院利用甲、乙两种原料为患者配制营养品. 已知每克甲原料含 0.6 单位蛋白质和 0.08 单位铁质,每克乙原料含 0.5 单位蛋白质和 0.04 单位铁质,如果患者每餐需 34 单位蛋白质和 4 单位铁质,那么每餐甲、乙两种原料各多少克恰好满足患者的需要?
【教材P122 练习 第1题】
解: 设每餐需要甲种原料 x g,乙种原料 y g.
根据题意,得
0.6x + 0.5y = 34,
0.08x + 0.04y = 4.
解方程组,得
x = 40,
y = 20.
答:每餐需要甲种原料 40 g,乙种原料 20 g 恰好满足患者的需要.
2. 向某地运送物资. 第一批 480 t,用 8 节火车车厢和20 辆卡车正好装完. 第二批 540 t,用 10 节火车车厢和 5 辆卡车正好装完,求每节火车车厢和每辆卡车分别能装多少吨.
【教材P122 练习 第2题】
解: 设每节火车车厢能装 x t,每辆卡车能装 y t.
根据题意,得
8x + 20y = 480,
10x + 5y = 540.
解方程组,得
x = 52.5,
y = 3.
解: 每节火车车厢能装 52.5 t,每辆卡车能装 3 t.
1星题 基础练
知识点1 调配问题
1.学校组织植树活动,已知在甲处植树的有23人,在乙处植树
的有17人,现调20人去支援,使在甲处植树的人数是乙处植
树人数的2倍.设调往甲处人,调往乙处 人,则可列方程组
为( )
B
A. B.
C. D.
2.(8分)[2025·滁州月考]甲、乙两车间各有工人若干名,若
从甲车间调100人给乙车间,则甲车间人数是乙车间人数的 ,
若从乙车间调100人给甲车间,则甲车间人数与乙车间人数
相同.甲、乙两车间分别原有多少名工人
解:设甲车间原有名工人,乙车间原有 名工人,
根据题意,得解得
答:甲车间原有180名工人,乙车间原有380名工人.
知识点2 配比问题
3.(8分)跨学科·化学 为了使某植物的长势更好,张叔叔决定
利用甲、乙两种肥料配制营养肥料.已知每克甲种肥料中含有
0.6单位镁元素和0.08单位铁元素,每克乙种肥料中含有0.5单
位镁元素和0.04单位铁元素.如果每次施肥需要34单位镁元素
和4单位铁元素,那么每次施肥需要甲、乙两种肥料各多少
克才能使该植物长势更好?
解:设每次施肥需要甲种肥料克、乙种肥料 克,根据题意
得解得
答:每次施肥需要甲种肥料40克、乙种肥料20克.
知识点3 配套问题
主图情境
生产中的数学智慧
工业生产如精密齿轮,各环节紧密配合,从工人的分工
协作到零件的配套生产,每一处都闪烁着数学智慧的光芒.
4.[2025年1月芜湖期末]在一家专注光学产品制造的车间里,
60名工人投入太阳镜的生产,1名工人每天可生产镜片200片或
镜架50个.每副太阳镜由2片镜片和1个镜架配成一套,应如何分
配工人生产镜片和镜架,才能使产品正好配套?设安排 名工
人生产镜片, 名工人生产镜架,则可列方程组为 ( )
D
A. B.
C. D.
5.某机械厂加工车间有85名工人,平均每人每天加工大齿轮16
个或小齿轮10个.已知2个大齿轮与3个小齿轮配成一套,安排
____名工人加工大齿轮,才能使每天加工的大小齿轮刚好配套.
25
6.(8分)某工厂计划生产一种新型豆浆机,每台豆浆机需3个 零
件和5个零件.已知车间每天能生产零件450个或 零件300
个.现在要求在21天中所生产的零件刚好配套,那么应安排多
少天生产零件,多少天生产 零件 这些零件可以满足生产多
少台豆浆机
解:设应安排天生产零件,天生产 零件.根据题意,得
解得
(个), (台).
答:应安排6天生产零件,15天生产 零件,这些零件可以
满足生产900台豆浆机.
2星题 中档练
7.[2025年1月大同期末]为提高病人免疫力,某医院精选甲、
乙两种食物为病人配制营养餐.已知每克甲种食物中铁的含量
是蛋白质的2倍,每克乙种食物中铁的含量是蛋白质的 .如果
病人每餐需要175个单位的蛋白质和200个单位的铁,每餐需
要甲、乙两种食物分别为140克、150克,则每克甲种食物中
含铁___个单位.
1
设每克甲种食物中含蛋白质 个单位,每克乙种食物
中含蛋白质 个单位.根据题意,得
解得
所以 ,所以每克甲种食物中含铁1个单位.
8.(12分)真实情境 为助力“零碳乡村”建设,某科技公司使用
新能源货车和智能物流无人机向乡村配送190套太阳能发电
设备,已知货车每辆可运送设备20套,无人机每架可运送设
备30套,货车和无人机一共用了8辆满载运送.
(1)小宇同学根据题意列出了一个尚不完整的方程组
请写出小宇所列方程组中未知数, 表示的
意义:表示________________, 表示__________________,
该方程组中“?”处的数应是___,“*”处的数应是_____;
使用货车的数量
使用无人机的数量
8
190
(2)小琼同学的思路是设货车运送套设备,无人机运送 套
设备.请你按照小琼的思路列出方程组,并求使用货车的数量;
解:依题意得解得
所以 .
答:使用货车5辆.
(3)如果每辆货车的运费是180元,每架无人机的运费是300元,
那么该公司运送这190套设备后的总运费是多少?
总运费为 (元).
答:该公司运送这190套设备后的总运费是1 800元.
9.(8分)[2025年1月合肥期末]某工厂生
产如图①所示的长方形和正方形纸板,
做成如图②所示的竖式与横式两种长方
体形状的无盖纸盒,其中竖式纸盒由4个长方形和1个正方形
纸板做成,横式纸盒由3个长方形和2个正方形纸板做成
(给定的长方形和正方形纸板都不用裁剪,也不考虑接缝).
(1)现有长方形纸板340个,正方形纸板
160个,做成上述两种纸盒,纸板恰好用
完,求两种纸盒的生产个数.
解:设做成的竖式纸盒有个,横式纸盒有 个,根据题意得
解得
答:做成的竖式纸盒有40个,横式纸盒有60个.
(2)纸板车间共有78名工人,每名工人一
天能生产70个长方形纸板或者100个正方
形纸板.已知一个竖式纸盒与一个横式纸
盒配套,要求纸板车间一天生产的纸板由其他车间做成的竖
式纸盒与横式纸盒配套,问纸板车间应如何安排工人生产这
两种纸板?
设分配名工人生产正方形纸板, 名工
人生产长方形纸板,由题意,
得解得
答:纸板车间应分配18名工人生产正方
形纸板,60名工人生产长方形纸板.
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
