3.6 三元一次方程组及其解法 课件(共30张PPT)
文档属性
| 名称 | 3.6 三元一次方程组及其解法 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
3.6 三元一次方程组及其解法
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
3.6 三元一次方程组及其解法
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
前面我们学习了二元一次方程组及其解法,知道了可以通过代入消元法或加减消元法将二元一次方程组转化为一元一次方程来求解。在实际问题中,有时会涉及到三个未知数,这就需要我们学习三元一次方程组及其解法。三元一次方程组的解法与二元一次方程组的解法类似,核心思想仍然是 “消元”。
学习目标
理解三元一次方程、三元一次方程组的概念,知道三元一次方程组的解的含义。
掌握三元一次方程组的解法,能运用代入消元法和加减消元法将三元一次方程组逐步转化为二元一次方程组,进而转化为一元一次方程求解。
经历用消元法解三元一次方程组的过程,进一步体会 “消元” 思想在解方程组中的作用。
提高分析问题和解决问题的能力,培养严谨的逻辑思维习惯。
知识点:三元一次方程和三元一次方程组的概念
三元一次方程
含有三个未知数,并且含有未知数的项的次数都是 1 的整式方程,叫做三元一次方程。
例如:\(x + y + z = 5\)、\(2x - 3y + z = 7\)都是三元一次方程。
三元一次方程组
由三个一次方程组成,并且含有三个未知数的方程组,叫做三元一次方程组。
例如:\(\begin{cases}x + y + z = 6\\x - y + z = 2\\2x + y - z = 1\end{cases}\)就是一个三元一次方程组。
三元一次方程组的解
使三元一次方程组中三个方程都成立的三个未知数的值,叫做三元一次方程组的解。
例如:\(\begin{cases}x = 1\\y = 2\\z = 3\end{cases}\)是方程组\(\begin{cases}x + y + z = 6\\x - y + z = 2\\2x + y - z = 1\end{cases}\)的解,因为将这三个值代入方程组中的每个方程,等式都成立。
知识点:三元一次方程组的解法
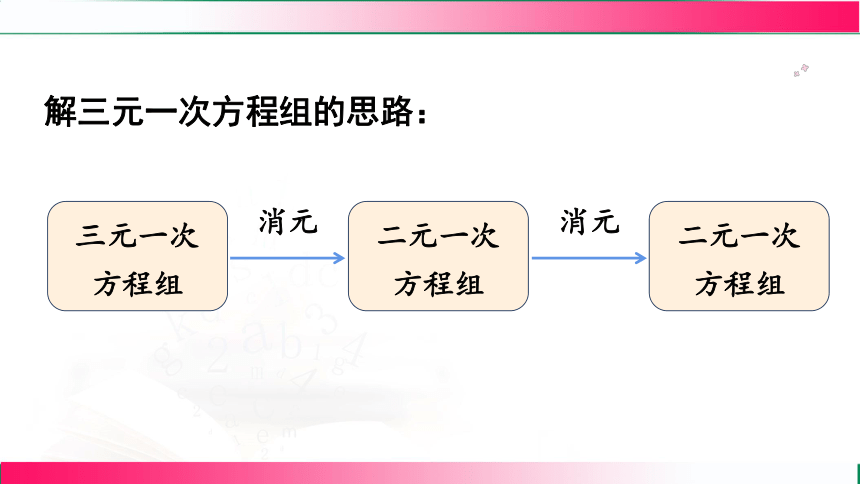
三元一次方程组的解法的基本思想是 “消元”,即通过代入消元法或加减消元法,逐步减少未知数的个数,把三元一次方程组转化为二元一次方程组,再把二元一次方程组转化为一元一次方程,进而求解。
解三元一次方程组的步骤
消元:从三元一次方程组中选择一个系数比较简单的方程,将其中一个未知数用含另外两个未知数的式子表示出来(代入消元法);或者通过对方程组中的方程进行加减运算,消去一个未知数,得到一个二元一次方程组(加减消元法)。
求解二元一次方程组:按照解二元一次方程组的方法,求出两个未知数的值。
回代:将求出的两个未知数的值代入之前用含这两个未知数的式子表示第三个未知数的方程中,求出第三个未知数的值。
检验:把求得的三个未知数的值代入原方程组中的三个方程,检验是否都是方程的解。
写出答案:用大括号 “\(\begin{cases}\end{cases}\)” 把三个未知数的值括起来,作为方程组的解。
例题解析
例 1:解方程组\(\begin{cases}x + y + z = 6& \\x - y + z = 2& \\2x + y - z = 1& \end{cases}\)
解:消元:用① - ②消去\(x\)和\(z\),得:\(
\begin{align*}
(x + y + z)-(x - y + z)&=6 - 2\\
x + y + z - x + y - z&=4\\
2y&=4\\
y&=2
\end{align*}
\)
用① + ③消去\(z\),得:\(
\begin{align*}
(x + y + z)+(2x + y - z)&=6 + 1\\
x + y + z + 2x + y - z&=7\\
3x + 2y&=7&
\end{align*}
\)
求解二元一次方程组:把\(y = 2\)代入④,得:\(
\begin{align*}
3x + 2 2&=7\\
3x + 4&=7\\
3x&=3\\
x&=1
\end{align*}
\)
回代:把\(x = 1\),\(y = 2\)代入①,得:\(
\begin{align*}
1 + 2 + z&=6\\
z&=3
\end{align*}
\)
检验:把\(x = 1\),\(y = 2\),\(z = 3\)代入原方程组:
①:左边\(=1 + 2 + 3 = 6\),右边\(=6\),左边 = 右边;
②:左边\(=1 - 2 + 3 = 2\),右边\(=2\),左边 = 右边;
③:左边\(=2 1 + 2 - 3 = 1\),右边\(=1\),左边 = 右边。
所以,方程组的解是\(\begin{cases}x = 1\\y = 2\\z = 3\end{cases}\)。
例 2:解方程组\(\begin{cases}3x + 4z = 7& \\2x + 3y + z = 9& \\5x - 9y + 7z = 8& \end{cases}\)
解:消元:先消去\(y\),②×3 + ③,得:\(
\begin{align*}
3(2x + 3y + z)+(5x - 9y + 7z)&=9 3 + 8\\
6x + 9y + 3z + 5x - 9y + 7z&=27 + 8\\
11x + 10z&=35&
\end{align*}
\)
由①得\(3x = 7 - 4z\),即\(x=\frac{7 - 4z}{3}\) ⑤
把⑤代入④,得:\(
\begin{align*}
11 \frac{7 - 4z}{3}+10z&=35\\
\frac{77 - 44z}{3}+10z&=35\\
77 - 44z + 30z&=105\\
-14z&=28\\
z&=-2
\end{align*}
\)
求解二元一次方程组:把\(z = -2\)代入⑤,得\(x=\frac{7 - 4 (-2)}{3}=\frac{7 + 8}{3}=5\)。
回代:把\(x = 5\),\(z = -2\)代入②,得:\(
\begin{align*}
2 5 + 3y + (-2)&=9\\
10 + 3y - 2&=9\\
3y + 8&=9\\
3y&=1\\
y&=\frac{1}{3}
\end{align*}
\)
检验:把\(x = 5\),\(y=\frac{1}{3}\),\(z = -2\)代入原方程组:
①:左边\(=3 5 + 4 (-2)=15 - 8 = 7\),右边\(=7\),左边 = 右边;
②:左边\(=2 5 + 3 \frac{1}{3}+(-2)=10 + 1 - 2 = 9\),右边\(=9\),左边 = 右边;
③:左边\(=5 5 - 9 \frac{1}{3}+7 (-2)=25 - 3 - 14 = 8\),右边\(=8\),左边 = 右边。
所以,方程组的解是\(\begin{cases}x = 5\\y=\frac{1}{3}\\z = -2\end{cases}\)。
例 3:解方程组\(\begin{cases}x:y = 3:2& \\y:z = 5:4& \\x + y + z = 66& \end{cases}\)
解:消元:由①得\(x=\frac{3}{2}y\) ④;由②得\(z=\frac{4}{5}y\) ⑤。
把④、⑤代入③,得:\(
\begin{align*}
\frac{3}{2}y + y + \frac{4}{5}y&=66\\
\frac{15}{10}y + \frac{10}{10}y + \frac{8}{10}y&=66\\
\frac{33}{10}y&=66\\
y&=20
\end{align*}
\)
求解二元一次方程组:把\(y = 20\)代入④,得\(x=\frac{3}{2} 20 = 30\);把\(y = 20\)代入⑤,得\(z=\frac{4}{5} 20 = 16\)。
检验:把\(x = 30\),\(y = 20\),\(z = 16\)代入③,左边\(=30 + 20 + 16 = 66\),右边\(=66\),左边 = 右边。且\(x:y = 30:20 = 3:2\),\(y:z = 20:16 = 5:4\),符合①②。
所以,方程组的解是\(\begin{cases}x = 30\\y = 20\\z = 16\end{cases}\)。
小练习
解下列三元一次方程组:
(1)\(\begin{cases}3x - y + z = 4& \\2x + 3y - z = 12& \\x + y + z = 6& \end{cases}\);
(2)\(\begin{cases}a - b + c = 0& \\4a + 2b + c = 3& \\25a + 5b + c = 60& \end{cases}\);
(3)\(\begin{cases}x + 2y = 3& \\y + 2z = 4& \\z + 2x = 5& \end{cases}\)。
已知方程组\(\begin{cases}x + y = 3\\y + z = -2\\z + x = 9\end{cases}\),求\(x + y + z\)的值。
若\(x\)、\(y\)、\(z\)满足\(\begin{cases}x + 2y - z = 4\\2x - y + z = 3\\3x + y - 2z = -1\end{cases}\),求\(x\)、\(y\)、\(z\)的值。
思考讨论
解三元一次方程组与解二元一次方程组有什么联系和区别?
联系:两者的核心思想都是 “消元”,都是通过消去未知数,将方程组转化为一元一次方程来求解。解三元一次方程组是在解二元一次方程组的基础上进行的,当三元一次方程组转化为二元一次方程组后,就可以按照解二元一次方程组的方法继续求解。
区别:三元一次方程组含有三个未知数,需要消去两个未知数才能转化为一元一次方程;而二元一次方程组含有两个未知数,只需消去一个未知数就能转化为一元一次方程。此外,三元一次方程组消元的过程可能更复杂,需要选择合适的消元方法和消元对象。
在解三元一次方程组时,如何选择消去哪个未知数?
在解三元一次方程组时,选择消去的未知数应遵循 “系数简单、运算简便” 的原则。一般来说,可以选择系数绝对值较小的未知数,或者选择在三个方程中出现次数较多且系数容易处理的未知数进行消去。例如,如果某个未知数在两个方程中的系数互为相反数或相等,那么先消去这个未知数会比较简便。
课堂小结
三元一次方程和三元一次方程组的概念:含有三个未知数,且含未知数的项的次数都是 1 的整式方程是三元一次方程;由三个这样的方程组成的方程组是三元一次方程组。
三元一次方程组的解法:基本思想是 “消元”,步骤是先消去一个未知数得到二元一次方程组,再解二元一次方程组得到两个未知数的值,然后回代求出第三个未知数的值,最后检验并写出答案。
解三元一次方程组时,要灵活运用代入消元法和加减消元法,选择合适的未知数进行消去,以简化计算过程。同时,要注意每一步计算的准确性,避免出现错误。
课后作业
解下列三元一次方程组:
(1)\(\begin{cases}2x + 3y + z = 6\\x - y + 2z = -1\\x + 2y - z = 5\end{cases}\);
(2)\(\begin{cases}3x + 4z = 14\\5x + 4y + z = 17\\4x - 5y + 8z = 36\end{cases}\);
(3)\(\begin{cases}\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\\x + y + z = 18\end{cases}\)。
已知\(x\)、\(y\)、\(z\)满足\(\begin{cases}2x - 3y = 8\\3y + 2z = 0\\x - z = -2\end{cases}\),求\(x + y + z\)的值。
一个三位数,个位、十位、百位上的数字之和为 12,个位数字与百位数字之和等于十位数字,百位数字的 3 倍比个位数字与十位数字的和大 2,求这个三位数。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
新课导入
5x + 4y = 18,
15x + 10y = 50.
3x + 2y + z = 39,
2x + 3y + z = 34,
x + 2y + 3z = 26.
二元一次方程组
?
由三个一次方程组成,且含三个未知数的方程组,叫作三元一次方程组.
探索新知
下列方程组是三元一次方程组的是( )
x + 2y = 1,
y + 2z = 2,
z + = 3.
a + b + c = 1,
a - b = 4,
4a – 2b + c = 7.
x2 - 4 = 0,
y + 1 = x,
x – z = -3.
-x + y + 3z = -1,
x – y + z = 3,
2x + m - z = 0.
A.
B.
C.
D.
B
三元一次方程组满足的条件:
(1)方程组中一共含有三个未知数;
(2)每个方程必须是一次方程;
(3)含有三个方程;
(4)必须是整式方程.
解二元一次方程组的消元法(加减法和代入法)是否也能用来解三元一次方程组呢?
思 考
x + y + 2z = 3, ①
-2x - y + z = -3, ②
x + 2y - 4z = -5. ③
解方程组:
例
1
解: 先用加减消元法消去 x.
② + ①×2,得
y + 5z = 3. ④
③ - ①,得
y - 6z = -8. ⑤
④ - ⑤,得
11z = 11.
下面解由④⑤联立成的二元一次方程组.
z = 1. ⑥
将⑥代入④,得
y = -2.
将 y,z 的值代入①,得
x = 3.
所以
x = 3,
y = -2,
z = 1.
y + 5z = 3. ④
y - 6z = -8. ⑤
巩固练习
解下列三元一次方程组:
(1)
x + 3y + 2z = 2, ①
3x + 2y - 4z = 3,②
2x–y = 7. ③
解:①×2 + ②,得 5x + 8y = 7. ④
③×8 + ④,得 21x = 63,
两边都除以 21,得 x = 3.
把 x 用 3 代入方程③,得 y = -1.
把 x 用 3,y 用 -1 代入方程①,
得 z = 1.
因此, 是原三元一次方程组
的解.
x = 3.
y = -1,
z = 1
(2)
x + y - z = 2, ①
2x - y + 3z = 2, ②
x–4y - 2z = -6. ③
① + ②,得 3x + 2z = 4. ④
①×4 + ③,得 5x-6z = 2.⑤
④×3+⑤,得 14x = 14,解得 x = 1.
把 x 用 1 代入方程④,得 z = 0.5.
把 x 用 1,z 用 0.5 代入方程①,
得 y = 1.5.
因此, 是原三元一次方程组
的解.
x = 1,
y = 1.5,
z = 0.5
解三元一次方程组的思路:
三元一次
方程组
二元一次
方程组
二元一次
方程组
消元
消元
解三元一次方程组的一般步骤:
(1)消元:利用代入消元法或加减消元法,把方程组中的一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另两个未知数的二元一次方程组.
(2)求解:解这个二元一次方程组,求出两个未知数的值.
(3)回代:将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个一元一次方程.
(4)求解:解这个一元一次方程,求出第三个未知数的值.
(5)写解:将求得的三个未知数的值用“{”写在一起,即是三元一次方程组的解.
某营养餐应包含 35 单位的铁、70 单位的钙和 35 单位的维生素. 现有一营养师根据上面的标准配餐,其中包含 A,B,C 三种食物. 下表给出的是每份(50 g)食物分别所含的铁、钙和维生素的量.
例
2
食物 铁/单位 钙/单位 维生素/单位
A 5 20 5
B 5 10 15
C 10 10 5
(1)设配餐中 A,B,C 三种食物分别为 x,y,z 份,
请根据题意列出方程组;
(2)解该三元一次方程组,求出满足要求的 A,B,C 的份数.
食物 铁/单位 钙/单位 维生素/单位
A 5 20 5
B 5 10 15
C 10 10 5
解:(1)设配餐中 A,B,C 三种食物分别为 x、y、z 份,由题意得
5x + 5y + 10z = 35, ①
20x + 10y + 10z = 70, ②
5x + 15y + 5z = 35. ③
食物 铁/单位 钙/单位 维生素/单位
A 5 20 5
B 5 10 15
C 10 10 5
(2)由①得 x = 7-y-2z. ④
将④代入②③,得
y + 3z = 7, ⑤
2y – z = 0. ⑥
解这个方程组,得
y = 1,
z = 2.
将 代入④,得 x = 2.
y = 1,
z = 2
所以
x = 2,
y = 1,
z = 2.
答:A 种食物 2 份,B 种食物 1 份,C 种食物 2 份.
食物 铁/单位 钙/单位 维生素/单位
A 5 20 5
B 5 10 15
C 10 10 5
已知甲、乙两数之和为 3,乙、丙两数之和为 6,甲、丙两数之和为 7,求这三个数.
例
3
解 设甲、乙、丙三数分别为 x,y,z,由题意得
x + y = 3, ①
y + z = 6, ②
x + z = 7. ③
①+②+③,两边同除以 2,得 x + y + z = 8. ④
④ - ① 得 z = 5,④ - ② 得 x = 2,④ - ③ 得 y = 1.
答:甲、乙、丙三数分别为 2,1,5.
练 习
【教材P127 练习 第1题】
1. 解下列方程组:
(1)
3x + y - 4z = 13,
5x - y + 3z = 5,
x + y–z = 3;
(2)
3x - y + z = 4,
2x + 3y - z = 12,
x + y + z = 6.
x = 2,
y = -1,
z = -2.
x = 2,
y = 3,
z = 1.
2. 某厂家生产甲、乙、丙三种型号的手机,出厂价分别为每部 3 600 元、1 200 元和 2 400 元. 一商场用 120 000 元购买上述三种型号手机共 40 部,其中甲型号手机比丙型号手机多 24 部. 求该商场购买上述三种型号手机各多少部.
【教材P127 练习 第2题】
解:设商场购买了甲型号手机 x 部,乙型号手机 y 部,丙型号手机 z 部.
x + y + z = 40,
3 600x + 1 200y + 2 400z = 120 000,
x - z = 24.
根据题意,得
x = 28,
y = 8,
z = 4.
解方程组,得
答:商场购买了甲型号手机 28 部,乙型号手机 8 部,丙型号手机 4 部.
1星题 基础练
知识点1 三元一次方程组的概念
1.下列方程组是三元一次方程组的是( )
B
A. B.
C. D.
知识点2 三元一次方程组的解法
2.解方程组 最简便的消元方法是( )
B
A.先消去 B.先消去
C.先消去 D.先消去常数项
3.(4分)解方程组:
解:由,得,由 ,得
,由,得,所以 ,
把代入①,得,把代入③,得 ,所以
方程组的解为
知识点3 三元一次方程组的简单应用
4.(8分)今年小新一家三口的年龄总和是80岁,爸爸比妈妈大3
岁,妈妈的年龄恰好是小新年龄的5倍.问:今年爸爸、妈妈和
小新分别几岁
解:设今年小新的年龄为岁,妈妈的年龄为 岁,爸爸的年
龄为 岁.
由题意,得解得
答:今年爸爸38岁,妈妈35岁,小新7岁.
2星题 中档练
5.已知方程组 与方程组
有相同的解,则___,___, ____.
2
3
6.[2025·合肥月考]已知,, 满足
,则 ___,
__, ___.
3
1
7.整 体 思 想 [2025年1月南京期末] 某商场出售甲、乙、
丙三种型号的商品,若购买甲2件,乙3件,丙1件,共需130
元;购买甲3件,乙5件,丙1件,共需205元.若购买甲、乙、
丙各1件,则需____元.
55
谢谢观看!
3.6 三元一次方程组及其解法
第3章 一次方程与方程组
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
3.6 三元一次方程组及其解法
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
前面我们学习了二元一次方程组及其解法,知道了可以通过代入消元法或加减消元法将二元一次方程组转化为一元一次方程来求解。在实际问题中,有时会涉及到三个未知数,这就需要我们学习三元一次方程组及其解法。三元一次方程组的解法与二元一次方程组的解法类似,核心思想仍然是 “消元”。
学习目标
理解三元一次方程、三元一次方程组的概念,知道三元一次方程组的解的含义。
掌握三元一次方程组的解法,能运用代入消元法和加减消元法将三元一次方程组逐步转化为二元一次方程组,进而转化为一元一次方程求解。
经历用消元法解三元一次方程组的过程,进一步体会 “消元” 思想在解方程组中的作用。
提高分析问题和解决问题的能力,培养严谨的逻辑思维习惯。
知识点:三元一次方程和三元一次方程组的概念
三元一次方程
含有三个未知数,并且含有未知数的项的次数都是 1 的整式方程,叫做三元一次方程。
例如:\(x + y + z = 5\)、\(2x - 3y + z = 7\)都是三元一次方程。
三元一次方程组
由三个一次方程组成,并且含有三个未知数的方程组,叫做三元一次方程组。
例如:\(\begin{cases}x + y + z = 6\\x - y + z = 2\\2x + y - z = 1\end{cases}\)就是一个三元一次方程组。
三元一次方程组的解
使三元一次方程组中三个方程都成立的三个未知数的值,叫做三元一次方程组的解。
例如:\(\begin{cases}x = 1\\y = 2\\z = 3\end{cases}\)是方程组\(\begin{cases}x + y + z = 6\\x - y + z = 2\\2x + y - z = 1\end{cases}\)的解,因为将这三个值代入方程组中的每个方程,等式都成立。
知识点:三元一次方程组的解法
三元一次方程组的解法的基本思想是 “消元”,即通过代入消元法或加减消元法,逐步减少未知数的个数,把三元一次方程组转化为二元一次方程组,再把二元一次方程组转化为一元一次方程,进而求解。
解三元一次方程组的步骤
消元:从三元一次方程组中选择一个系数比较简单的方程,将其中一个未知数用含另外两个未知数的式子表示出来(代入消元法);或者通过对方程组中的方程进行加减运算,消去一个未知数,得到一个二元一次方程组(加减消元法)。
求解二元一次方程组:按照解二元一次方程组的方法,求出两个未知数的值。
回代:将求出的两个未知数的值代入之前用含这两个未知数的式子表示第三个未知数的方程中,求出第三个未知数的值。
检验:把求得的三个未知数的值代入原方程组中的三个方程,检验是否都是方程的解。
写出答案:用大括号 “\(\begin{cases}\end{cases}\)” 把三个未知数的值括起来,作为方程组的解。
例题解析
例 1:解方程组\(\begin{cases}x + y + z = 6& \\x - y + z = 2& \\2x + y - z = 1& \end{cases}\)
解:消元:用① - ②消去\(x\)和\(z\),得:\(
\begin{align*}
(x + y + z)-(x - y + z)&=6 - 2\\
x + y + z - x + y - z&=4\\
2y&=4\\
y&=2
\end{align*}
\)
用① + ③消去\(z\),得:\(
\begin{align*}
(x + y + z)+(2x + y - z)&=6 + 1\\
x + y + z + 2x + y - z&=7\\
3x + 2y&=7&
\end{align*}
\)
求解二元一次方程组:把\(y = 2\)代入④,得:\(
\begin{align*}
3x + 2 2&=7\\
3x + 4&=7\\
3x&=3\\
x&=1
\end{align*}
\)
回代:把\(x = 1\),\(y = 2\)代入①,得:\(
\begin{align*}
1 + 2 + z&=6\\
z&=3
\end{align*}
\)
检验:把\(x = 1\),\(y = 2\),\(z = 3\)代入原方程组:
①:左边\(=1 + 2 + 3 = 6\),右边\(=6\),左边 = 右边;
②:左边\(=1 - 2 + 3 = 2\),右边\(=2\),左边 = 右边;
③:左边\(=2 1 + 2 - 3 = 1\),右边\(=1\),左边 = 右边。
所以,方程组的解是\(\begin{cases}x = 1\\y = 2\\z = 3\end{cases}\)。
例 2:解方程组\(\begin{cases}3x + 4z = 7& \\2x + 3y + z = 9& \\5x - 9y + 7z = 8& \end{cases}\)
解:消元:先消去\(y\),②×3 + ③,得:\(
\begin{align*}
3(2x + 3y + z)+(5x - 9y + 7z)&=9 3 + 8\\
6x + 9y + 3z + 5x - 9y + 7z&=27 + 8\\
11x + 10z&=35&
\end{align*}
\)
由①得\(3x = 7 - 4z\),即\(x=\frac{7 - 4z}{3}\) ⑤
把⑤代入④,得:\(
\begin{align*}
11 \frac{7 - 4z}{3}+10z&=35\\
\frac{77 - 44z}{3}+10z&=35\\
77 - 44z + 30z&=105\\
-14z&=28\\
z&=-2
\end{align*}
\)
求解二元一次方程组:把\(z = -2\)代入⑤,得\(x=\frac{7 - 4 (-2)}{3}=\frac{7 + 8}{3}=5\)。
回代:把\(x = 5\),\(z = -2\)代入②,得:\(
\begin{align*}
2 5 + 3y + (-2)&=9\\
10 + 3y - 2&=9\\
3y + 8&=9\\
3y&=1\\
y&=\frac{1}{3}
\end{align*}
\)
检验:把\(x = 5\),\(y=\frac{1}{3}\),\(z = -2\)代入原方程组:
①:左边\(=3 5 + 4 (-2)=15 - 8 = 7\),右边\(=7\),左边 = 右边;
②:左边\(=2 5 + 3 \frac{1}{3}+(-2)=10 + 1 - 2 = 9\),右边\(=9\),左边 = 右边;
③:左边\(=5 5 - 9 \frac{1}{3}+7 (-2)=25 - 3 - 14 = 8\),右边\(=8\),左边 = 右边。
所以,方程组的解是\(\begin{cases}x = 5\\y=\frac{1}{3}\\z = -2\end{cases}\)。
例 3:解方程组\(\begin{cases}x:y = 3:2& \\y:z = 5:4& \\x + y + z = 66& \end{cases}\)
解:消元:由①得\(x=\frac{3}{2}y\) ④;由②得\(z=\frac{4}{5}y\) ⑤。
把④、⑤代入③,得:\(
\begin{align*}
\frac{3}{2}y + y + \frac{4}{5}y&=66\\
\frac{15}{10}y + \frac{10}{10}y + \frac{8}{10}y&=66\\
\frac{33}{10}y&=66\\
y&=20
\end{align*}
\)
求解二元一次方程组:把\(y = 20\)代入④,得\(x=\frac{3}{2} 20 = 30\);把\(y = 20\)代入⑤,得\(z=\frac{4}{5} 20 = 16\)。
检验:把\(x = 30\),\(y = 20\),\(z = 16\)代入③,左边\(=30 + 20 + 16 = 66\),右边\(=66\),左边 = 右边。且\(x:y = 30:20 = 3:2\),\(y:z = 20:16 = 5:4\),符合①②。
所以,方程组的解是\(\begin{cases}x = 30\\y = 20\\z = 16\end{cases}\)。
小练习
解下列三元一次方程组:
(1)\(\begin{cases}3x - y + z = 4& \\2x + 3y - z = 12& \\x + y + z = 6& \end{cases}\);
(2)\(\begin{cases}a - b + c = 0& \\4a + 2b + c = 3& \\25a + 5b + c = 60& \end{cases}\);
(3)\(\begin{cases}x + 2y = 3& \\y + 2z = 4& \\z + 2x = 5& \end{cases}\)。
已知方程组\(\begin{cases}x + y = 3\\y + z = -2\\z + x = 9\end{cases}\),求\(x + y + z\)的值。
若\(x\)、\(y\)、\(z\)满足\(\begin{cases}x + 2y - z = 4\\2x - y + z = 3\\3x + y - 2z = -1\end{cases}\),求\(x\)、\(y\)、\(z\)的值。
思考讨论
解三元一次方程组与解二元一次方程组有什么联系和区别?
联系:两者的核心思想都是 “消元”,都是通过消去未知数,将方程组转化为一元一次方程来求解。解三元一次方程组是在解二元一次方程组的基础上进行的,当三元一次方程组转化为二元一次方程组后,就可以按照解二元一次方程组的方法继续求解。
区别:三元一次方程组含有三个未知数,需要消去两个未知数才能转化为一元一次方程;而二元一次方程组含有两个未知数,只需消去一个未知数就能转化为一元一次方程。此外,三元一次方程组消元的过程可能更复杂,需要选择合适的消元方法和消元对象。
在解三元一次方程组时,如何选择消去哪个未知数?
在解三元一次方程组时,选择消去的未知数应遵循 “系数简单、运算简便” 的原则。一般来说,可以选择系数绝对值较小的未知数,或者选择在三个方程中出现次数较多且系数容易处理的未知数进行消去。例如,如果某个未知数在两个方程中的系数互为相反数或相等,那么先消去这个未知数会比较简便。
课堂小结
三元一次方程和三元一次方程组的概念:含有三个未知数,且含未知数的项的次数都是 1 的整式方程是三元一次方程;由三个这样的方程组成的方程组是三元一次方程组。
三元一次方程组的解法:基本思想是 “消元”,步骤是先消去一个未知数得到二元一次方程组,再解二元一次方程组得到两个未知数的值,然后回代求出第三个未知数的值,最后检验并写出答案。
解三元一次方程组时,要灵活运用代入消元法和加减消元法,选择合适的未知数进行消去,以简化计算过程。同时,要注意每一步计算的准确性,避免出现错误。
课后作业
解下列三元一次方程组:
(1)\(\begin{cases}2x + 3y + z = 6\\x - y + 2z = -1\\x + 2y - z = 5\end{cases}\);
(2)\(\begin{cases}3x + 4z = 14\\5x + 4y + z = 17\\4x - 5y + 8z = 36\end{cases}\);
(3)\(\begin{cases}\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\\x + y + z = 18\end{cases}\)。
已知\(x\)、\(y\)、\(z\)满足\(\begin{cases}2x - 3y = 8\\3y + 2z = 0\\x - z = -2\end{cases}\),求\(x + y + z\)的值。
一个三位数,个位、十位、百位上的数字之和为 12,个位数字与百位数字之和等于十位数字,百位数字的 3 倍比个位数字与十位数字的和大 2,求这个三位数。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
新课导入
5x + 4y = 18,
15x + 10y = 50.
3x + 2y + z = 39,
2x + 3y + z = 34,
x + 2y + 3z = 26.
二元一次方程组
?
由三个一次方程组成,且含三个未知数的方程组,叫作三元一次方程组.
探索新知
下列方程组是三元一次方程组的是( )
x + 2y = 1,
y + 2z = 2,
z + = 3.
a + b + c = 1,
a - b = 4,
4a – 2b + c = 7.
x2 - 4 = 0,
y + 1 = x,
x – z = -3.
-x + y + 3z = -1,
x – y + z = 3,
2x + m - z = 0.
A.
B.
C.
D.
B
三元一次方程组满足的条件:
(1)方程组中一共含有三个未知数;
(2)每个方程必须是一次方程;
(3)含有三个方程;
(4)必须是整式方程.
解二元一次方程组的消元法(加减法和代入法)是否也能用来解三元一次方程组呢?
思 考
x + y + 2z = 3, ①
-2x - y + z = -3, ②
x + 2y - 4z = -5. ③
解方程组:
例
1
解: 先用加减消元法消去 x.
② + ①×2,得
y + 5z = 3. ④
③ - ①,得
y - 6z = -8. ⑤
④ - ⑤,得
11z = 11.
下面解由④⑤联立成的二元一次方程组.
z = 1. ⑥
将⑥代入④,得
y = -2.
将 y,z 的值代入①,得
x = 3.
所以
x = 3,
y = -2,
z = 1.
y + 5z = 3. ④
y - 6z = -8. ⑤
巩固练习
解下列三元一次方程组:
(1)
x + 3y + 2z = 2, ①
3x + 2y - 4z = 3,②
2x–y = 7. ③
解:①×2 + ②,得 5x + 8y = 7. ④
③×8 + ④,得 21x = 63,
两边都除以 21,得 x = 3.
把 x 用 3 代入方程③,得 y = -1.
把 x 用 3,y 用 -1 代入方程①,
得 z = 1.
因此, 是原三元一次方程组
的解.
x = 3.
y = -1,
z = 1
(2)
x + y - z = 2, ①
2x - y + 3z = 2, ②
x–4y - 2z = -6. ③
① + ②,得 3x + 2z = 4. ④
①×4 + ③,得 5x-6z = 2.⑤
④×3+⑤,得 14x = 14,解得 x = 1.
把 x 用 1 代入方程④,得 z = 0.5.
把 x 用 1,z 用 0.5 代入方程①,
得 y = 1.5.
因此, 是原三元一次方程组
的解.
x = 1,
y = 1.5,
z = 0.5
解三元一次方程组的思路:
三元一次
方程组
二元一次
方程组
二元一次
方程组
消元
消元
解三元一次方程组的一般步骤:
(1)消元:利用代入消元法或加减消元法,把方程组中的一个方程与另两个方程分别组成两组,消去两组中的同一个未知数,得到关于另两个未知数的二元一次方程组.
(2)求解:解这个二元一次方程组,求出两个未知数的值.
(3)回代:将求得的两个未知数的值代入原方程组中的一个系数比较简单的方程,得到一个一元一次方程.
(4)求解:解这个一元一次方程,求出第三个未知数的值.
(5)写解:将求得的三个未知数的值用“{”写在一起,即是三元一次方程组的解.
某营养餐应包含 35 单位的铁、70 单位的钙和 35 单位的维生素. 现有一营养师根据上面的标准配餐,其中包含 A,B,C 三种食物. 下表给出的是每份(50 g)食物分别所含的铁、钙和维生素的量.
例
2
食物 铁/单位 钙/单位 维生素/单位
A 5 20 5
B 5 10 15
C 10 10 5
(1)设配餐中 A,B,C 三种食物分别为 x,y,z 份,
请根据题意列出方程组;
(2)解该三元一次方程组,求出满足要求的 A,B,C 的份数.
食物 铁/单位 钙/单位 维生素/单位
A 5 20 5
B 5 10 15
C 10 10 5
解:(1)设配餐中 A,B,C 三种食物分别为 x、y、z 份,由题意得
5x + 5y + 10z = 35, ①
20x + 10y + 10z = 70, ②
5x + 15y + 5z = 35. ③
食物 铁/单位 钙/单位 维生素/单位
A 5 20 5
B 5 10 15
C 10 10 5
(2)由①得 x = 7-y-2z. ④
将④代入②③,得
y + 3z = 7, ⑤
2y – z = 0. ⑥
解这个方程组,得
y = 1,
z = 2.
将 代入④,得 x = 2.
y = 1,
z = 2
所以
x = 2,
y = 1,
z = 2.
答:A 种食物 2 份,B 种食物 1 份,C 种食物 2 份.
食物 铁/单位 钙/单位 维生素/单位
A 5 20 5
B 5 10 15
C 10 10 5
已知甲、乙两数之和为 3,乙、丙两数之和为 6,甲、丙两数之和为 7,求这三个数.
例
3
解 设甲、乙、丙三数分别为 x,y,z,由题意得
x + y = 3, ①
y + z = 6, ②
x + z = 7. ③
①+②+③,两边同除以 2,得 x + y + z = 8. ④
④ - ① 得 z = 5,④ - ② 得 x = 2,④ - ③ 得 y = 1.
答:甲、乙、丙三数分别为 2,1,5.
练 习
【教材P127 练习 第1题】
1. 解下列方程组:
(1)
3x + y - 4z = 13,
5x - y + 3z = 5,
x + y–z = 3;
(2)
3x - y + z = 4,
2x + 3y - z = 12,
x + y + z = 6.
x = 2,
y = -1,
z = -2.
x = 2,
y = 3,
z = 1.
2. 某厂家生产甲、乙、丙三种型号的手机,出厂价分别为每部 3 600 元、1 200 元和 2 400 元. 一商场用 120 000 元购买上述三种型号手机共 40 部,其中甲型号手机比丙型号手机多 24 部. 求该商场购买上述三种型号手机各多少部.
【教材P127 练习 第2题】
解:设商场购买了甲型号手机 x 部,乙型号手机 y 部,丙型号手机 z 部.
x + y + z = 40,
3 600x + 1 200y + 2 400z = 120 000,
x - z = 24.
根据题意,得
x = 28,
y = 8,
z = 4.
解方程组,得
答:商场购买了甲型号手机 28 部,乙型号手机 8 部,丙型号手机 4 部.
1星题 基础练
知识点1 三元一次方程组的概念
1.下列方程组是三元一次方程组的是( )
B
A. B.
C. D.
知识点2 三元一次方程组的解法
2.解方程组 最简便的消元方法是( )
B
A.先消去 B.先消去
C.先消去 D.先消去常数项
3.(4分)解方程组:
解:由,得,由 ,得
,由,得,所以 ,
把代入①,得,把代入③,得 ,所以
方程组的解为
知识点3 三元一次方程组的简单应用
4.(8分)今年小新一家三口的年龄总和是80岁,爸爸比妈妈大3
岁,妈妈的年龄恰好是小新年龄的5倍.问:今年爸爸、妈妈和
小新分别几岁
解:设今年小新的年龄为岁,妈妈的年龄为 岁,爸爸的年
龄为 岁.
由题意,得解得
答:今年爸爸38岁,妈妈35岁,小新7岁.
2星题 中档练
5.已知方程组 与方程组
有相同的解,则___,___, ____.
2
3
6.[2025·合肥月考]已知,, 满足
,则 ___,
__, ___.
3
1
7.整 体 思 想 [2025年1月南京期末] 某商场出售甲、乙、
丙三种型号的商品,若购买甲2件,乙3件,丙1件,共需130
元;购买甲3件,乙5件,丙1件,共需205元.若购买甲、乙、
丙各1件,则需____元.
55
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
