4.3.2线段的中线及线段的基本事实 课件(共30张PPT)
文档属性
| 名称 | 4.3.2线段的中线及线段的基本事实 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 21:10:22 | ||
图片预览









文档简介
(共30张PPT)
4.3.2线段的中线及线段的基本事实
第4章 几何图形初步
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
4.3.2 线段的中线及线段的基本事实
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
上节课我们学习了比较线段长短的两种方法 —— 叠合法和度量法,还掌握了线段的基本事实 “两点之间,线段最短”,知道了两点之间的距离是指两点之间线段的长度。本节课我们将学习线段的一个重要概念 —— 线段的中点,以及由中点延伸出的线段中线,同时进一步巩固线段的基本事实。
学习目标
理解线段中点的概念,能准确表述线段中点的性质。
掌握线段中线的含义,能结合图形识别线段的中线。
能运用线段中点的性质解决线段长度的计算问题。
进一步巩固 “两点之间,线段最短” 这一基本事实,并能灵活运用。
培养逻辑推理能力和几何语言表达能力,提高解决几何问题的能力。
知识点:线段的中点
概念
把一条线段分成两条相等线段的点,叫做这条线段的中点。
图形表示
如图,点 M 是线段 AB 的中点,意味着 AM=MB,且 AM=MB=\(\frac{1}{2}\)AB,AB=2AM=2MB。
A——M——B
性质
若点 M 是线段 AB 的中点,则有:
AM=MB
AM=\(\frac{1}{2}\)AB
MB=\(\frac{1}{2}\)AB
AB=2AM=2MB
这些性质是解决线段长度计算问题的重要依据,在解题时可以根据需要灵活选用。
实例
生活中也有很多线段中点的例子,比如一根绳子的中点,将绳子对折后,两端重合的点就是绳子的中点;一根直尺上刻度 5cm 的位置,是刻度 0cm 和刻度 10cm 之间线段的中点。
知识点:线段的中线
含义
在三角形中,连接一个顶点和它所对边的中点的线段叫做三角形的中线。
图形表示
如图,在△ABC 中,点 D 是 BC 边的中点,那么线段 AD 就是△ABC 的一条中线。
A
/ \
/ \
B——D——C
特征
三角形的中线是一条线段,它的一个端点是三角形的顶点,另一个端点是该顶点所对边的中点。
一个三角形有三条中线,这三条中线相交于一点,这个点叫做三角形的重心。
实例
在三角形框架中,连接一个顶点和对边中点的线段就是该三角形的中线,它可以将三角形分成两个面积相等的小三角形,这一性质在几何图形的面积计算中经常用到。
知识点:线段基本事实的回顾与拓展
基本事实回顾
“两点之间,线段最短”:两点之间的所有连线中,线段的长度最短,这条线段的长度叫做这两点之间的距离。
拓展应用
最短路径问题:在平面图形中,求从一个点到另一个点的最短路径,通常可以利用 “两点之间,线段最短” 来解决。例如,在一个长方形中,从一个顶点到对角顶点的最短路径是长方形的对角线,因为对角线是连接这两个顶点的线段。
距离的计算:根据两点之间的距离是两点之间线段的长度,我们可以通过测量线段的长度来得到两点之间的距离,也可以根据线段的和差关系计算两点之间的距离。
例题解析
例 1:已知线段 AB=8cm,点 C 是线段 AB 的中点,求 AC 和 BC 的长度。
解:因为点 C 是线段 AB 的中点,根据线段中点的性质,AC=BC=\(\frac{1}{2}\)AB。
已知 AB=8cm,所以 AC=BC=\(\frac{1}{2}\times8=4\)cm。
答:AC 的长度是 4cm,BC 的长度是 4cm。
例 2:如图,在△ABC 中,AD 是 BC 边上的中线,已知 BC=10cm,求 BD 和 DC 的长度。
A
/ \
/ \
B——D——C
解:因为 AD 是 BC 边上的中线,所以点 D 是 BC 的中点,根据线段中点的性质,BD=DC=\(\frac{1}{2}\)BC。
已知 BC=10cm,所以 BD=DC=\(\frac{1}{2}\times10=5\)cm。
答:BD 的长度是 5cm,DC 的长度是 5cm。
例 3:如图,点 M 是线段 AB 上的一点,AM=5cm,MB=3cm,点 N 是线段 AM 的中点,求线段 AN 和 NB 的长度。
A——N——M——B
解:因为点 N 是线段 AM 的中点,所以 AN=\(\frac{1}{2}\)AM。
已知 AM=5cm,所以 AN=\(\frac{1}{2}\times5=2.5\)cm。
又因为 NB=NM+MB,且 NM=AN=2.5cm,MB=3cm,所以 NB=2.5+3=5.5cm。
答:线段 AN 的长度是 2.5cm,线段 NB 的长度是 5.5cm。
例 4:如图,从点 A 到点 B 有四条路线,分别是①A→C→B;②A→D→B;③A→E→B;④A→B。请指出最短的路线,并说明理由。
A
|
|
C D E
| | |
| | |
B
解:最短的路线是④A→B。
理由是根据线段的基本事实 “两点之间,线段最短”,点 A 和点 B 之间的所有连线中,线段 AB 的长度最短,而其他三条路线都是折线,长度都大于线段 AB 的长度。
小练习
填空题:
(1)若点 M 是线段 AB 的中点,AB=12cm,则 AM=______cm,BM=______cm。
(2)在△ABC 中,BE 是 AC 边上的中线,AC=8cm,则 AE=______cm,EC=______cm。
(3)两点之间的所有连线中,最短,这条线段的长度叫做。
选择题:
(1)下列说法正确的是( )
A. 线段的中点有两个
B. 三角形的中线是射线
C. 若点 P 是线段 AB 的中点,则 AP=PB
D. 两点之间的距离是指两点之间的直线长度
(2)如图,点 C 是线段 AB 上的一点,点 M 是 AC 的中点,点 N 是 BC 的中点,若 AB=10cm,则 MN 的长度是( )
A——M——C——N——B
A. 3cm B. 4cm C. 5cm D. 6cm
解答题:
(1)已知线段 AB=16cm,点 C 在 AB 的延长线上,点 D 是线段 BC 的中点,且 CD=3cm,求线段 AC 的长度。
(2)在△ABC 中,AB=AC=10cm,AD 是 BC 边上的中线,AD=8cm,求 BC 的长度。
思考讨论
线段的中点一定在这条线段上吗?为什么?
线段的中点一定在这条线段上。因为线段的中点是将线段分成两条相等线段的点,只有在线段上才能满足这一条件,如果点在线段的延长线上,就无法将线段分成两条相等的线段,所以线段的中点必然在这条线段上。
一个三角形有几条中线?这些中线有什么位置关系?
一个三角形有三条中线,分别连接三个顶点和它所对边的中点。三角形的三条中线相交于一点,这个点叫做三角形的重心。重心到顶点的距离是它到对边中点距离的 2 倍,这是三角形重心的一个重要性质。
课堂小结
线段的中点:把一条线段分成两条相等线段的点,具有 AM=MB=\(\frac{1}{2}\)AB,AB=2AM=2MB 等性质,是解决线段长度计算的关键。
线段的中线:在三角形中,连接一个顶点和它所对边的中点的线段,一个三角形有三条中线,它们相交于三角形的重心。
线段的基本事实:“两点之间,线段最短”,两点之间的距离是指两点之间线段的长度,在解决最短路径和距离计算问题中有着重要应用。
通过本节课的学习,我们对线段的相关知识有了更深入的理解,掌握了线段中点和中线的概念及性质,能运用这些知识解决线段长度的计算问题,同时进一步巩固了线段的基本事实,为后续学习更复杂的几何知识打下了基础。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
线段AB上有一点C,且点C到点A,B的距离相等,那么点C是线段AB的什么点呢?
C
B
A
如图,点C在线段AB上,且AC=CB,
像这样把一条线段分成两条相等的线段的点,叫作线段的中点.
此时,AC=CB= AB 或 AB=2AC=2CB.
新知探究
知识点1
线段的中点
A
B
C
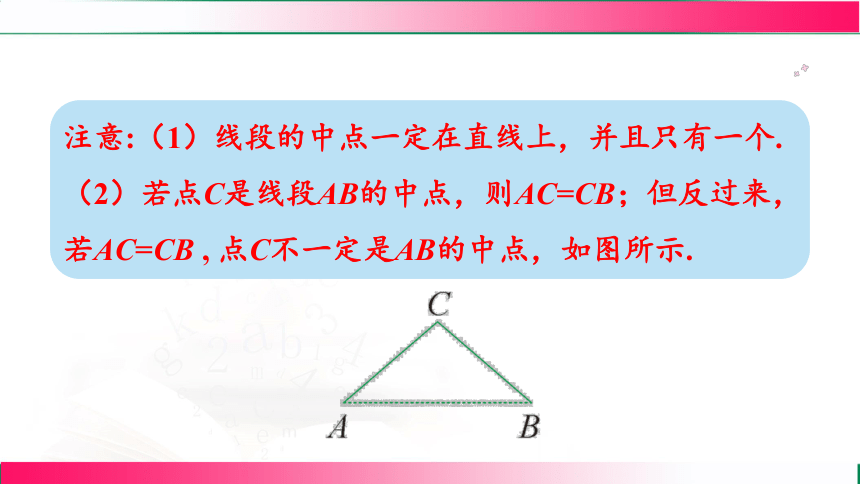
注意:(1)线段的中点一定在直线上,并且只有一个.
(2)若点C是线段AB的中点,则AC=CB;但反过来,若AC=CB , 点C不一定是AB的中点,如图所示.
知识拓展:
线段的三等分点:如图,若点C,D将线段AB分成相等的三条线段AC,CD,DB,则点C,D叫作线段AB的三等分点,这时AC=CD=DB= AB(类似地,还有四等分点、五等分点等).
解:如图,
因为AB=4,点D为AB的中点,所以AD= AB=2.
又因为AC=11,点E为AC中点,所以AE= AC =5.5.
所以DE=AE-AD =5.5-2 =3.5.
例 3 已知线段AB=4,延长AB至点C,使AC=11.点D是AB的中点,点E是AC的中点,求DE的长.
A
C
D
B
E
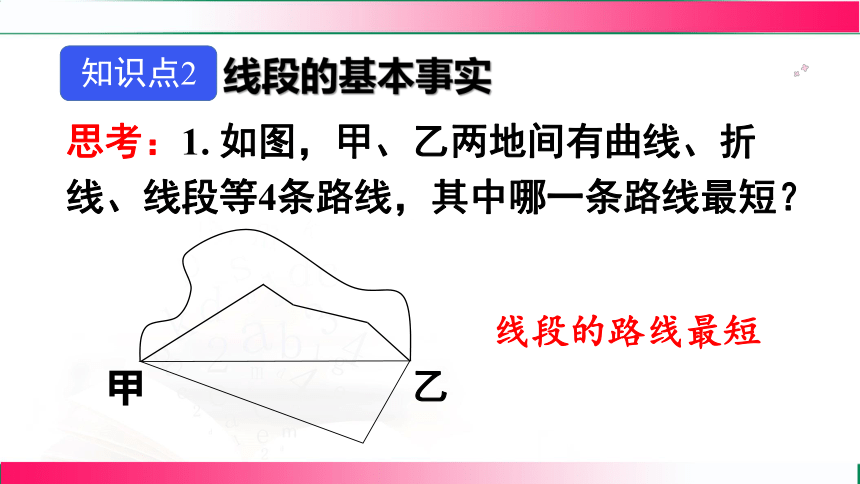
思考:1. 如图,甲、乙两地间有曲线、折线、线段等4条路线,其中哪一条路线最短?
甲
乙
线段的路线最短
知识点2
线段的基本事实
思考:2. 如图,人们修建公路遇到大山阻隔时,常会打一条隧道直穿过去,为什么?
因为修隧道可以缩短两地之间的路程, 实现路途近的目的。
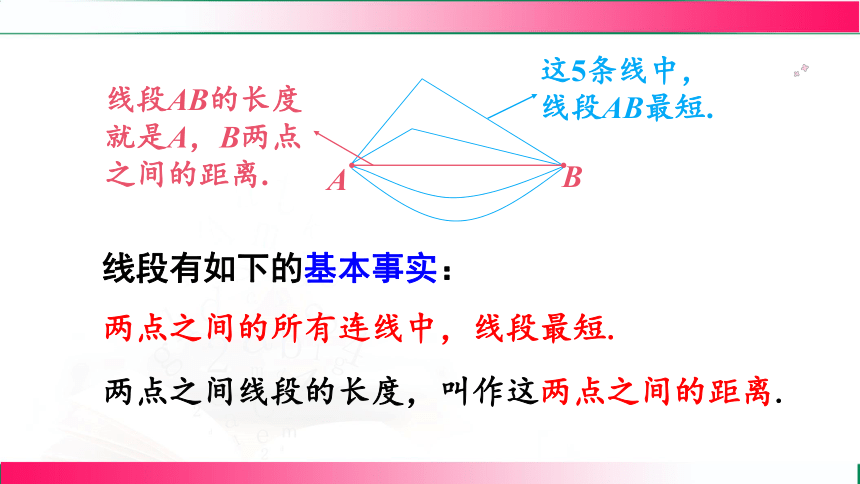
线段有如下的基本事实:
两点之间的所有连线中,线段最短.
两点之间线段的长度,叫作这两点之间的距离.
这5条线中,
线段AB最短.
线段AB的长度就是A,B两点之间的距离.
A
B
注意:
(1)两点间的距离是一个具体的数量,而线段是图形,因此不能把A,B两点间的距离说成线段AB;
(2)两点间的连线是指以两个点为端点的任意线,包括线段、折线和曲线,有无数条.
1. 如图,P是线段MN的中点,那么MN=____MP=____PN,MP=PN=______MN.
练习
M
N
P
2
2
【教材P152 练习 第1题】
2. 如图,用刻度尺量出AB,AC,BC的长度,并比较AB+AC与BC的长短.不通过测量,你能比较AB+AC与BC的长短吗?依据是什么?
A
B
C
解:
AB+AC >BC.
能,依据是“两点之间的所有连线中,线段最短”.
【教材P152 练习 第2题】
1.下列说法中正确的是( )
A.连结两点的线段叫作两点间的距离
B.在所有连接两点的线中,直线最短
C.线段AB就是表示点A到点B的距离
D.点A到点B的距离就是线段AB的长度
D
随堂练习
2.已知A、B、C三点在同一直线上,如果
线段AB=6cm,BC=3cm,A、C两点的
距离为d,那么( )
A. d=9cm B. d=3cm
C. d=9cm或d=3cm D. d大小不确定
C
3.如图,已知线段AB=6 cm,C是AB的中点,D是AC的中点,求线段BD的长.
A
B
C
D
解:因为AB=6 cm,C是AB的中点,
所以AC=BC= AB=3 cm.
因为D是AC的中点,所以AD=CD= AC=1.5 cm.
所以BD=BC+CD=3+1.5=4.5 ( cm ).
1星题 基础练
知识点1 线段的中点
1.[知识初练]下列条件中能确定是线段 的中点的是
( )
C
A. B.
C. D.
2.如图,,,为线段的中点,则 的长度
为( )
D
A.5 B.4 C.3 D.2
3.如图,是线段的中点,点,把线段三等分.已知 的
长为1,则线段 的长为___.
6
知识点2 线段的基本事实以及两点间距离
4., 两点间的距离是( )
D
A.连接两点的直线 B.连接两点的线段
C.连接两点的直线的长度 D.连接两点的线段的长度
5.[2024·厦门十一中期末]如图,一只蚂蚁外出觅食,它与
食物间有三条路径,从上到下依次记为①,②,③,则蚂蚁
选择第____条路径最近,理由是__________________.
②
两点之间线段最短
2星题 中档练
6.分类讨论思想 如图,为线段的中点, ,若点
在直线上,且,则 的长为______.
3或7
7.(12分)[2025年1月安庆期末改编]如图,已知点, 在线
段上,且 .
(1)比较线段的长度:___(填“ ”“”或“ ”);
(2)已知,,是的中点,是 的中点,求线
段 的长度;
解:由题意得.因为 是
的中点,是 的中点,所以
,所以
.
(3)在(2)中,如果,,其他条件不变,那么
_________(用含, 的式子表示).
8.(12分)[2025·佛山月考]平面上有, ,
, 四个村庄,为解决当地缺水问题,政府
准备投资修建一个蓄水池,不考虑其他因素,
请你画图确定蓄水池 的位置,使它与四个村庄的距离之和最
小,,,四个村庄的地理位置如图所示 ,并说明理由.
解:如图所示,连接,交于点,点 就是蓄水池的位
置,这一点到,,, 四个村庄的距离之和最小.理由:
两点之间的所有连线中,线段最短.
1.线段的基本事实:
两点之间的所有的连线中,线段最短.
2.两点之间线段的长度,叫作这两点之间的距离.
课堂小结
谢谢观看!
4.3.2线段的中线及线段的基本事实
第4章 几何图形初步
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
4.3.2 线段的中线及线段的基本事实
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
上节课我们学习了比较线段长短的两种方法 —— 叠合法和度量法,还掌握了线段的基本事实 “两点之间,线段最短”,知道了两点之间的距离是指两点之间线段的长度。本节课我们将学习线段的一个重要概念 —— 线段的中点,以及由中点延伸出的线段中线,同时进一步巩固线段的基本事实。
学习目标
理解线段中点的概念,能准确表述线段中点的性质。
掌握线段中线的含义,能结合图形识别线段的中线。
能运用线段中点的性质解决线段长度的计算问题。
进一步巩固 “两点之间,线段最短” 这一基本事实,并能灵活运用。
培养逻辑推理能力和几何语言表达能力,提高解决几何问题的能力。
知识点:线段的中点
概念
把一条线段分成两条相等线段的点,叫做这条线段的中点。
图形表示
如图,点 M 是线段 AB 的中点,意味着 AM=MB,且 AM=MB=\(\frac{1}{2}\)AB,AB=2AM=2MB。
A——M——B
性质
若点 M 是线段 AB 的中点,则有:
AM=MB
AM=\(\frac{1}{2}\)AB
MB=\(\frac{1}{2}\)AB
AB=2AM=2MB
这些性质是解决线段长度计算问题的重要依据,在解题时可以根据需要灵活选用。
实例
生活中也有很多线段中点的例子,比如一根绳子的中点,将绳子对折后,两端重合的点就是绳子的中点;一根直尺上刻度 5cm 的位置,是刻度 0cm 和刻度 10cm 之间线段的中点。
知识点:线段的中线
含义
在三角形中,连接一个顶点和它所对边的中点的线段叫做三角形的中线。
图形表示
如图,在△ABC 中,点 D 是 BC 边的中点,那么线段 AD 就是△ABC 的一条中线。
A
/ \
/ \
B——D——C
特征
三角形的中线是一条线段,它的一个端点是三角形的顶点,另一个端点是该顶点所对边的中点。
一个三角形有三条中线,这三条中线相交于一点,这个点叫做三角形的重心。
实例
在三角形框架中,连接一个顶点和对边中点的线段就是该三角形的中线,它可以将三角形分成两个面积相等的小三角形,这一性质在几何图形的面积计算中经常用到。
知识点:线段基本事实的回顾与拓展
基本事实回顾
“两点之间,线段最短”:两点之间的所有连线中,线段的长度最短,这条线段的长度叫做这两点之间的距离。
拓展应用
最短路径问题:在平面图形中,求从一个点到另一个点的最短路径,通常可以利用 “两点之间,线段最短” 来解决。例如,在一个长方形中,从一个顶点到对角顶点的最短路径是长方形的对角线,因为对角线是连接这两个顶点的线段。
距离的计算:根据两点之间的距离是两点之间线段的长度,我们可以通过测量线段的长度来得到两点之间的距离,也可以根据线段的和差关系计算两点之间的距离。
例题解析
例 1:已知线段 AB=8cm,点 C 是线段 AB 的中点,求 AC 和 BC 的长度。
解:因为点 C 是线段 AB 的中点,根据线段中点的性质,AC=BC=\(\frac{1}{2}\)AB。
已知 AB=8cm,所以 AC=BC=\(\frac{1}{2}\times8=4\)cm。
答:AC 的长度是 4cm,BC 的长度是 4cm。
例 2:如图,在△ABC 中,AD 是 BC 边上的中线,已知 BC=10cm,求 BD 和 DC 的长度。
A
/ \
/ \
B——D——C
解:因为 AD 是 BC 边上的中线,所以点 D 是 BC 的中点,根据线段中点的性质,BD=DC=\(\frac{1}{2}\)BC。
已知 BC=10cm,所以 BD=DC=\(\frac{1}{2}\times10=5\)cm。
答:BD 的长度是 5cm,DC 的长度是 5cm。
例 3:如图,点 M 是线段 AB 上的一点,AM=5cm,MB=3cm,点 N 是线段 AM 的中点,求线段 AN 和 NB 的长度。
A——N——M——B
解:因为点 N 是线段 AM 的中点,所以 AN=\(\frac{1}{2}\)AM。
已知 AM=5cm,所以 AN=\(\frac{1}{2}\times5=2.5\)cm。
又因为 NB=NM+MB,且 NM=AN=2.5cm,MB=3cm,所以 NB=2.5+3=5.5cm。
答:线段 AN 的长度是 2.5cm,线段 NB 的长度是 5.5cm。
例 4:如图,从点 A 到点 B 有四条路线,分别是①A→C→B;②A→D→B;③A→E→B;④A→B。请指出最短的路线,并说明理由。
A
|
|
C D E
| | |
| | |
B
解:最短的路线是④A→B。
理由是根据线段的基本事实 “两点之间,线段最短”,点 A 和点 B 之间的所有连线中,线段 AB 的长度最短,而其他三条路线都是折线,长度都大于线段 AB 的长度。
小练习
填空题:
(1)若点 M 是线段 AB 的中点,AB=12cm,则 AM=______cm,BM=______cm。
(2)在△ABC 中,BE 是 AC 边上的中线,AC=8cm,则 AE=______cm,EC=______cm。
(3)两点之间的所有连线中,最短,这条线段的长度叫做。
选择题:
(1)下列说法正确的是( )
A. 线段的中点有两个
B. 三角形的中线是射线
C. 若点 P 是线段 AB 的中点,则 AP=PB
D. 两点之间的距离是指两点之间的直线长度
(2)如图,点 C 是线段 AB 上的一点,点 M 是 AC 的中点,点 N 是 BC 的中点,若 AB=10cm,则 MN 的长度是( )
A——M——C——N——B
A. 3cm B. 4cm C. 5cm D. 6cm
解答题:
(1)已知线段 AB=16cm,点 C 在 AB 的延长线上,点 D 是线段 BC 的中点,且 CD=3cm,求线段 AC 的长度。
(2)在△ABC 中,AB=AC=10cm,AD 是 BC 边上的中线,AD=8cm,求 BC 的长度。
思考讨论
线段的中点一定在这条线段上吗?为什么?
线段的中点一定在这条线段上。因为线段的中点是将线段分成两条相等线段的点,只有在线段上才能满足这一条件,如果点在线段的延长线上,就无法将线段分成两条相等的线段,所以线段的中点必然在这条线段上。
一个三角形有几条中线?这些中线有什么位置关系?
一个三角形有三条中线,分别连接三个顶点和它所对边的中点。三角形的三条中线相交于一点,这个点叫做三角形的重心。重心到顶点的距离是它到对边中点距离的 2 倍,这是三角形重心的一个重要性质。
课堂小结
线段的中点:把一条线段分成两条相等线段的点,具有 AM=MB=\(\frac{1}{2}\)AB,AB=2AM=2MB 等性质,是解决线段长度计算的关键。
线段的中线:在三角形中,连接一个顶点和它所对边的中点的线段,一个三角形有三条中线,它们相交于三角形的重心。
线段的基本事实:“两点之间,线段最短”,两点之间的距离是指两点之间线段的长度,在解决最短路径和距离计算问题中有着重要应用。
通过本节课的学习,我们对线段的相关知识有了更深入的理解,掌握了线段中点和中线的概念及性质,能运用这些知识解决线段长度的计算问题,同时进一步巩固了线段的基本事实,为后续学习更复杂的几何知识打下了基础。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
情境导入
线段AB上有一点C,且点C到点A,B的距离相等,那么点C是线段AB的什么点呢?
C
B
A
如图,点C在线段AB上,且AC=CB,
像这样把一条线段分成两条相等的线段的点,叫作线段的中点.
此时,AC=CB= AB 或 AB=2AC=2CB.
新知探究
知识点1
线段的中点
A
B
C
注意:(1)线段的中点一定在直线上,并且只有一个.
(2)若点C是线段AB的中点,则AC=CB;但反过来,若AC=CB , 点C不一定是AB的中点,如图所示.
知识拓展:
线段的三等分点:如图,若点C,D将线段AB分成相等的三条线段AC,CD,DB,则点C,D叫作线段AB的三等分点,这时AC=CD=DB= AB(类似地,还有四等分点、五等分点等).
解:如图,
因为AB=4,点D为AB的中点,所以AD= AB=2.
又因为AC=11,点E为AC中点,所以AE= AC =5.5.
所以DE=AE-AD =5.5-2 =3.5.
例 3 已知线段AB=4,延长AB至点C,使AC=11.点D是AB的中点,点E是AC的中点,求DE的长.
A
C
D
B
E
思考:1. 如图,甲、乙两地间有曲线、折线、线段等4条路线,其中哪一条路线最短?
甲
乙
线段的路线最短
知识点2
线段的基本事实
思考:2. 如图,人们修建公路遇到大山阻隔时,常会打一条隧道直穿过去,为什么?
因为修隧道可以缩短两地之间的路程, 实现路途近的目的。
线段有如下的基本事实:
两点之间的所有连线中,线段最短.
两点之间线段的长度,叫作这两点之间的距离.
这5条线中,
线段AB最短.
线段AB的长度就是A,B两点之间的距离.
A
B
注意:
(1)两点间的距离是一个具体的数量,而线段是图形,因此不能把A,B两点间的距离说成线段AB;
(2)两点间的连线是指以两个点为端点的任意线,包括线段、折线和曲线,有无数条.
1. 如图,P是线段MN的中点,那么MN=____MP=____PN,MP=PN=______MN.
练习
M
N
P
2
2
【教材P152 练习 第1题】
2. 如图,用刻度尺量出AB,AC,BC的长度,并比较AB+AC与BC的长短.不通过测量,你能比较AB+AC与BC的长短吗?依据是什么?
A
B
C
解:
AB+AC >BC.
能,依据是“两点之间的所有连线中,线段最短”.
【教材P152 练习 第2题】
1.下列说法中正确的是( )
A.连结两点的线段叫作两点间的距离
B.在所有连接两点的线中,直线最短
C.线段AB就是表示点A到点B的距离
D.点A到点B的距离就是线段AB的长度
D
随堂练习
2.已知A、B、C三点在同一直线上,如果
线段AB=6cm,BC=3cm,A、C两点的
距离为d,那么( )
A. d=9cm B. d=3cm
C. d=9cm或d=3cm D. d大小不确定
C
3.如图,已知线段AB=6 cm,C是AB的中点,D是AC的中点,求线段BD的长.
A
B
C
D
解:因为AB=6 cm,C是AB的中点,
所以AC=BC= AB=3 cm.
因为D是AC的中点,所以AD=CD= AC=1.5 cm.
所以BD=BC+CD=3+1.5=4.5 ( cm ).
1星题 基础练
知识点1 线段的中点
1.[知识初练]下列条件中能确定是线段 的中点的是
( )
C
A. B.
C. D.
2.如图,,,为线段的中点,则 的长度
为( )
D
A.5 B.4 C.3 D.2
3.如图,是线段的中点,点,把线段三等分.已知 的
长为1,则线段 的长为___.
6
知识点2 线段的基本事实以及两点间距离
4., 两点间的距离是( )
D
A.连接两点的直线 B.连接两点的线段
C.连接两点的直线的长度 D.连接两点的线段的长度
5.[2024·厦门十一中期末]如图,一只蚂蚁外出觅食,它与
食物间有三条路径,从上到下依次记为①,②,③,则蚂蚁
选择第____条路径最近,理由是__________________.
②
两点之间线段最短
2星题 中档练
6.分类讨论思想 如图,为线段的中点, ,若点
在直线上,且,则 的长为______.
3或7
7.(12分)[2025年1月安庆期末改编]如图,已知点, 在线
段上,且 .
(1)比较线段的长度:___(填“ ”“”或“ ”);
(2)已知,,是的中点,是 的中点,求线
段 的长度;
解:由题意得.因为 是
的中点,是 的中点,所以
,所以
.
(3)在(2)中,如果,,其他条件不变,那么
_________(用含, 的式子表示).
8.(12分)[2025·佛山月考]平面上有, ,
, 四个村庄,为解决当地缺水问题,政府
准备投资修建一个蓄水池,不考虑其他因素,
请你画图确定蓄水池 的位置,使它与四个村庄的距离之和最
小,,,四个村庄的地理位置如图所示 ,并说明理由.
解:如图所示,连接,交于点,点 就是蓄水池的位
置,这一点到,,, 四个村庄的距离之和最小.理由:
两点之间的所有连线中,线段最短.
1.线段的基本事实:
两点之间的所有的连线中,线段最短.
2.两点之间线段的长度,叫作这两点之间的距离.
课堂小结
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
