4.5.3用尺规作角 课件(共30张PPT)
文档属性
| 名称 | 4.5.3用尺规作角 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-13 00:00:00 | ||
图片预览




文档简介
(共30张PPT)
4.5.3用尺规作角
第4章 几何图形初步
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
4.5.3 用尺规作角
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
在前面对角的学习中,我们已经掌握了角的定义、表示方法、度量与比较,以及补角和余角的相关知识。本节课我们将学习一种重要的几何作图方法 —— 用尺规作角,即只用圆规和没有刻度的直尺来作出一个角等于已知角。这种作图方法不依赖于度量工具,是几何推理和作图的基础技能。
学习目标
了解尺规作图的含义和基本工具(圆规、无刻度直尺)。
掌握用尺规作一个角等于已知角的步骤,并能独立完成作图。
理解作图的原理,能结合图形说明每一步操作的依据。
培养动手操作能力和几何推理能力,感受尺规作图的严谨性和逻辑性。
知识点:尺规作图的基本概念
定义
尺规作图是指只用圆规和没有刻度的直尺来完成的作图方法。其中,直尺的作用是连接两点或延长线段,圆规的作用是画圆或圆弧,截取等长的线段。
特点
不使用度量工具,作图的准确性依赖于圆规截取等长线段和直尺连接直线的规范性。
每一步操作都有严格的几何依据,体现了几何的逻辑性和严谨性。
知识点:用尺规作一个角等于已知角
已知
一个角∠AOB。
求作
一个角∠A'O'B',使∠A'O'B'=∠AOB。
作图步骤
作射线 O'A':
用直尺画一条射线 O'A',作为要作的角的一边。这是角的起始边,相当于已知角∠AOB 的边 OA。
以点 O 为圆心,任意长为半径画弧:
用圆规的针尖固定在已知角的顶点 O 处,选取一个适当的长度作为半径(半径的长度可以任意,但在后续步骤中要保持一致),画一条弧,分别交 OA 于点 C,交 OB 于点 D。
依据:圆的定义(到定点的距离等于定长的点的集合),此时 OC=OD(同圆的半径相等)。
以点 O' 为圆心,OC 的长为半径画弧:
保持圆规的半径不变(即与步骤 2 中截取的 OC 长度相等),将圆规的针尖固定在射线 O'A' 的端点 O' 处,画一条弧,交 O'A' 于点 C'。
依据:圆规截取等长线段,此时 O'C'=OC=OD。
以点 C' 为圆心,CD 的长为半径画弧:
用圆规量取已知角上弧 CD 的长度(即圆规的针尖固定在点 C,笔尖调整到点 D 处),然后将圆规的针尖固定在点 C' 处,画一条弧,与步骤 3 中所画的弧交于点 D'。
依据:等长线段截取,此时 C'D'=CD。
过点 D' 作射线 O'B':
用直尺连接点 O' 和点 D',并延长为射线 O'B'。
此时,∠A'O'B' 即为所求作的角,且∠A'O'B'=∠AOB。
作图图示
已知角∠AOB:
A
/|
/ |
/ |C
O |
\ |
\ |D
\|
B
作图过程:
1. 作射线O'A':
O'——A'
2. 以O为圆心画弧交OA于C,交OB于D:
A
/|
/ |
/ |C
O———|——D
\ |
\ |
\|
B
3. 以O'为圆心,OC为半径画弧交O'A'于C':
O'——C'——A'
4. 以C'为圆心,CD为半径画弧交前弧于D':
O'——C'——A'
\
\
D'
5. 作射线O'B':
D'
/
/
O'——C'——A'
\
\
B'
最终∠A'O'B'=∠AOB
作图原理
在△OCD 和△O'C'D' 中:
OC=O'C'(步骤 2 和 3 中截取的半径相等)
CD=C'D'(步骤 4 中截取的弧长相等)
OD=O'D'(步骤 2 和 3 中截取的半径相等)
根据 “边边边”(SSS)全等判定定理,△OCD≌△O'C'D',因此对应角相等,即∠COD=∠C'O'D',也就是∠AOB=∠A'O'B'。这就是用尺规作一个角等于已知角的理论依据。
例题解析
例 1:已知∠α,用尺规作一个角,使它等于∠α 的 2 倍。
解:作法如下:
作∠AOB=∠α(按上述用尺规作一个角等于已知角的步骤)。
以点 O 为顶点,OB 为一边,在∠AOB 的外部作∠BOC=∠α。
则∠AOC=∠AOB+∠BOC=∠α+∠α=2∠α,∠AOC 即为所求作的角。
例 2:用尺规作图,已知∠1 和∠2,作一个角等于∠1+∠2。
解:作法如下:
作射线 OA。
以 O 为顶点,OA 为一边,作∠AOB=∠1。
以 O 为顶点,OB 为一边,在∠AOB 的外部作∠BOC=∠2。
则∠AOC=∠AOB+∠BOC=∠1+∠2,∠AOC 即为所求作的角。
小练习
填空题:
(1)尺规作图的工具是______和______。
(2)用尺规作一个角等于已知角时,第 2 步和第 3 步都要画弧,其中第 2 步是以______为圆心,第 3 步是以______为圆心,且这两步画弧的半径______。
(3)用尺规作角的理论依据是全等三角形的______判定定理(SSS)。
作图题:
(1)已知∠ABC,用尺规作一个角等于∠ABC。
(2)已知∠α 和∠β(∠α>∠β),用尺规作一个角等于∠α-∠β。
简答题:
(1)在 “用尺规作一个角等于已知角” 的步骤中,为什么要保证 OC=O'C',CD=C'D',OD=O'D'?
(2)用尺规作角与用量角器画角有什么不同?
思考讨论
除了作一个角等于已知角,你认为用尺规还能作出哪些特殊角?(如 60°、30° 等)
可以作出 60° 角:因为等边三角形的三个角都是 60°,所以可以用尺规作一个等边三角形,其中的一个角就是 60°。具体步骤:作一条线段 AB,以 A 为圆心,AB 为半径画弧,以 B 为圆心,AB 为半径画弧,两弧交于点 C,连接 AC 和 BC,则∠CAB=60°。
在此基础上,可以作出 30° 角(作 60° 角的角平分线)、90° 角(作两个 60° 角的和减去 30° 角,或利用等腰直角三角形)等。
尺规作图在几何学习中的意义是什么?
尺规作图是几何的基本技能之一,它不依赖于度量,能培养学生的动手操作能力和空间想象能力;每一步操作都有严格的几何依据,有助于学生理解几何概念和定理,培养逻辑推理能力;同时,尺规作图体现了几何的严谨性和逻辑性,是后续学习复杂几何作图和证明的基础。
课堂小结
尺规作图的定义:只用圆规和无刻度直尺进行的作图,强调不依赖度量,注重操作的规范性和依据的逻辑性。
用尺规作一个角等于已知角的步骤:
作射线(起始边);
已知角上画弧(定半径,得两点);
新作射线上画弧(同半径,得对应点);
截取等长弧(定另一点);
作射线(终边)。
作图原理:通过构造全等三角形(SSS),保证所作角与已知角相等。
通过本节课的学习,我们掌握了用尺规作一个角等于已知角的方法,理解了作图的原理和每一步操作的依据。这种作图方法是几何学习中的重要工具,在后续学习角的和差、角平分线的作图等内容时会经常用到,希望同学们勤加练习,熟练掌握。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
图形的绘制,图案的设计,时常需要画线段和角.
新课导入
之前我们已经学会了用尺规作线段,那我们这节课来学一下如何用尺规作角吧!
新知探究
知识点
作一个角等于已知角
例 3 已知∠M,画∠AOB,使得∠AOB=∠M.
M
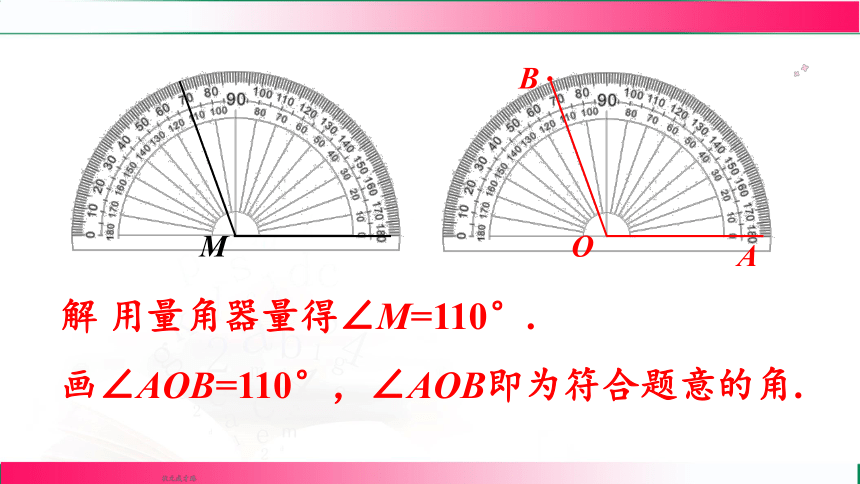
解 用量角器量得∠M=110°.
画∠AOB=110°,∠AOB即为符合题意的角.
M
O
A
B
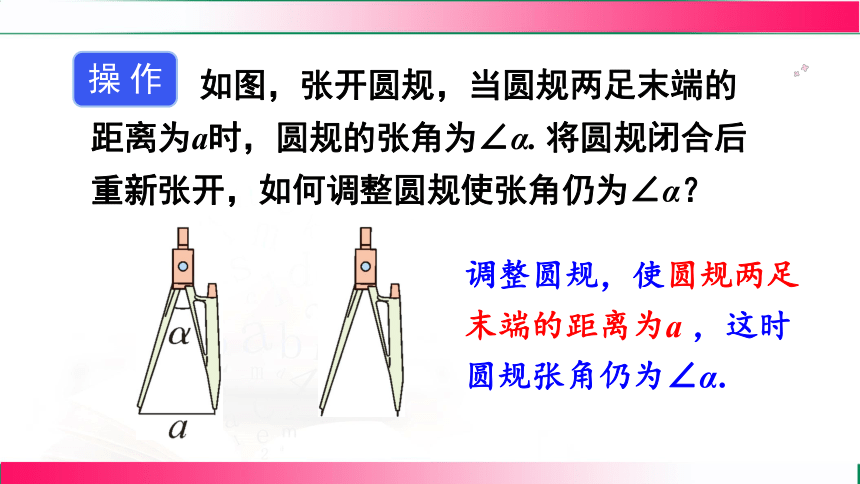
操 作
如图,张开圆规,当圆规两足末端的距离为a时,圆规的张角为∠α. 将圆规闭合后重新张开,如何调整圆规使张角仍为∠α?
调整圆规,使圆规两足末端的距离为a ,这时圆规张角仍为∠α.
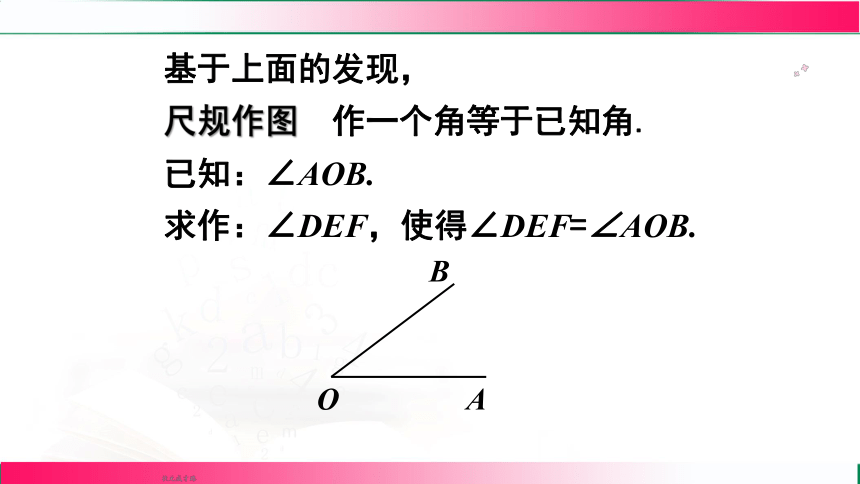
基于上面的发现,
尺规作图 作一个角等于已知角.
已知:∠AOB.
求作:∠DEF,使得∠DEF=∠AOB.
A
O
B
作法:(1)作射线EG.
(2)在∠AOB上以点O 为圆心,任意长为半径画弧,分别交射线OA和OB于点P,Q;
(3)以点E为圆心,线段OP长为半径画弧,交射线EG于点D.
A
O
B
E
G
P
Q
D
A
O
B
E
G
P
Q
D
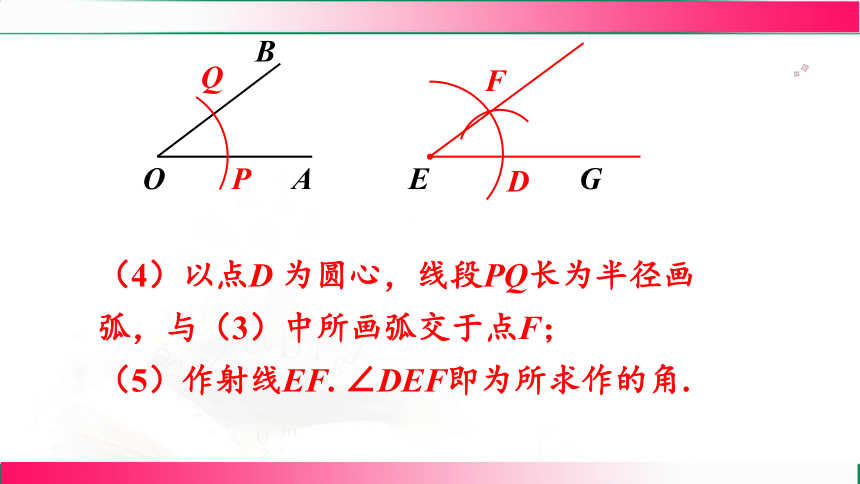
(4)以点D 为圆心,线段PQ长为半径画弧,与(3)中所画弧交于点F;
(5)作射线EF. ∠DEF即为所求作的角.
F
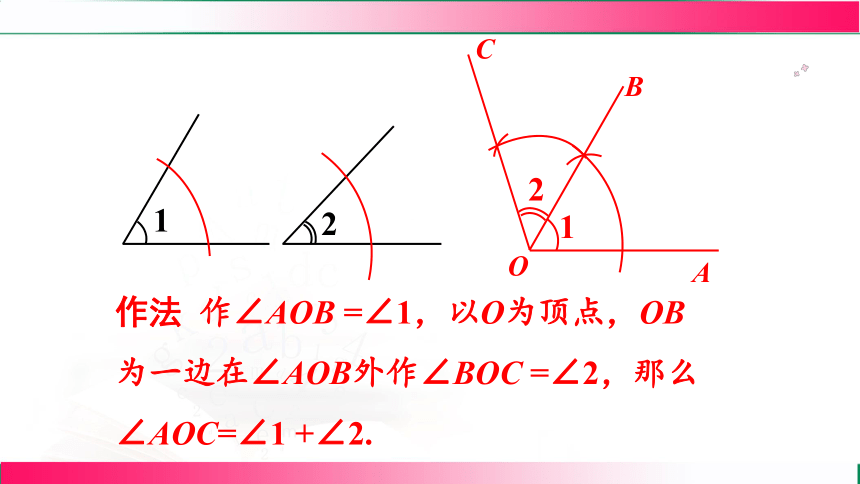
例 4 如图,已知两个角∠1和∠2(∠1>∠2),求作这两个角的和.
1
2
作法 作∠AOB =∠1,以O为顶点,OB为一边在∠AOB外作∠BOC =∠2,那么∠AOC=∠1 +∠2.
1
2
O
A
B
C
1
2
1.如图,已知∠α,用尺规作∠AOB=2∠α.
练习
α
【教材P162 练习 第1题】
解:如图所示.
作法:(1)作射线OD.
(2)以∠α的顶点M为圆心,任意长为半径画弧,分别与∠α的两边交于点P,Q.
(3)以点О为圆心,线段MP长为半径画弧,交射线OD于点A.
(4)以点A为圆心,线段PQ长为半径画弧,与(3)中所画弧交于点E.
(5)以点E为圆心,线段PQ长为半径画弧,交(3)中所画弧于点B(不在OD上).
(6)作射线OB.∠AOB=2∠α即为所求作的角.
2.参考例4,作给定两角的差.
α
β
【教材P162 练习 第2题】
解:如图所示.已知∠α,∠β,求作∠α-∠β.
作法:①作∠AOC= ∠α.
②以点О为角的顶点,OC为一边,在∠AOC的内部作∠COB=∠β,则∠AOB= ∠α-∠β即为所求作的角.
1. 如图,利用尺规作图作∠AOC=∠AOB的第一步是以点О为圆心、适当长为半径作弧①,分别交OA、OB于点E、F,那么作图痕迹②的作法是( )
A. 以点F为圆心、OE长为半径作弧
B. 以点F为圆心、EF长为半径作弧
C. 以点E为圆心、OE长为半径作弧
D. 以点E为圆心、EF长为半径作弧
随堂练习
D
2. 如图①,以点B为顶点,射线BC为一边,利用尺规作图在∠CAD内部作∠EBC,使∠EBC=∠A.
解:如图②,以点B为顶点,BC为一边在∠CAD内部作∠EBC=∠A. ∠EBC即为所求作的角.
3. 如图①,已知∠α,∠β,求作一个角使它等于2∠α-∠β(保留作图痕迹,不写作法).
解: 如图,∠AOC即为所求作的2∠α-∠β.
1星题 基础练
知识点 利用尺规作一个角等于已知角
1.如图,作一个角等于已知角
(尺规作图)的正确顺序是
____________.(填序号)
2.如图,用尺规作图作的第一步是以点 为圆
心,任意长为半径画弧①,分别交,于点, ,那么
第二步的作图痕迹②的作法是( )
D
A.以点为圆心, 长为半径画弧
B.以点为圆心, 长为半径画弧
C.以点为圆心, 长为半径画弧
D.以点为圆心, 长为半径画弧
3.(8分)如图,已知 , ,作一个角,使它等于 与
的和.(不写作法,保留作图痕迹)
解:如图, 即为所求作.
2星题 中档练
4.如图, , ,根据图中尺规作
图的痕迹,可知____ .
35
5.(8分)[2025·上海月考]如图,已知 和 ,利用尺规
作,使 .
解:如图, 即为所求作的角.
3星题 提升练
6.(8分)真实情境 小亮的一张地图上有,, 三个城市,
地图上的城市被墨迹污染了(如图),但知道 ,
,请你用尺规作图的方法帮他在图中确定 城市
的具体位置.(保留作图痕迹,不写作法)
解:如图,点 即为所求.
课堂小结
步骤 作图
(1)作射线EG
(2)在∠AOB上以点O为圆心,任意长为半径画弧,分别交射线OA和OB于点P,Q
(3)以点E为圆心,线段OP长为半径画弧,交射线EG于点D
(4)以点D为圆心,线段PQ长为半径画弧,与(3)中所画弧交于点F
(5)作射线EF.∠DEF即为所求作的角
用尺规作∠DEF=∠AOB的步骤:
谢谢观看!
4.5.3用尺规作角
第4章 几何图形初步
【2025-2026学年】2024沪科版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
4.5.3 用尺规作角
汇报人:[教师姓名]
汇报班级:[具体班级]
知识回顾
在前面对角的学习中,我们已经掌握了角的定义、表示方法、度量与比较,以及补角和余角的相关知识。本节课我们将学习一种重要的几何作图方法 —— 用尺规作角,即只用圆规和没有刻度的直尺来作出一个角等于已知角。这种作图方法不依赖于度量工具,是几何推理和作图的基础技能。
学习目标
了解尺规作图的含义和基本工具(圆规、无刻度直尺)。
掌握用尺规作一个角等于已知角的步骤,并能独立完成作图。
理解作图的原理,能结合图形说明每一步操作的依据。
培养动手操作能力和几何推理能力,感受尺规作图的严谨性和逻辑性。
知识点:尺规作图的基本概念
定义
尺规作图是指只用圆规和没有刻度的直尺来完成的作图方法。其中,直尺的作用是连接两点或延长线段,圆规的作用是画圆或圆弧,截取等长的线段。
特点
不使用度量工具,作图的准确性依赖于圆规截取等长线段和直尺连接直线的规范性。
每一步操作都有严格的几何依据,体现了几何的逻辑性和严谨性。
知识点:用尺规作一个角等于已知角
已知
一个角∠AOB。
求作
一个角∠A'O'B',使∠A'O'B'=∠AOB。
作图步骤
作射线 O'A':
用直尺画一条射线 O'A',作为要作的角的一边。这是角的起始边,相当于已知角∠AOB 的边 OA。
以点 O 为圆心,任意长为半径画弧:
用圆规的针尖固定在已知角的顶点 O 处,选取一个适当的长度作为半径(半径的长度可以任意,但在后续步骤中要保持一致),画一条弧,分别交 OA 于点 C,交 OB 于点 D。
依据:圆的定义(到定点的距离等于定长的点的集合),此时 OC=OD(同圆的半径相等)。
以点 O' 为圆心,OC 的长为半径画弧:
保持圆规的半径不变(即与步骤 2 中截取的 OC 长度相等),将圆规的针尖固定在射线 O'A' 的端点 O' 处,画一条弧,交 O'A' 于点 C'。
依据:圆规截取等长线段,此时 O'C'=OC=OD。
以点 C' 为圆心,CD 的长为半径画弧:
用圆规量取已知角上弧 CD 的长度(即圆规的针尖固定在点 C,笔尖调整到点 D 处),然后将圆规的针尖固定在点 C' 处,画一条弧,与步骤 3 中所画的弧交于点 D'。
依据:等长线段截取,此时 C'D'=CD。
过点 D' 作射线 O'B':
用直尺连接点 O' 和点 D',并延长为射线 O'B'。
此时,∠A'O'B' 即为所求作的角,且∠A'O'B'=∠AOB。
作图图示
已知角∠AOB:
A
/|
/ |
/ |C
O |
\ |
\ |D
\|
B
作图过程:
1. 作射线O'A':
O'——A'
2. 以O为圆心画弧交OA于C,交OB于D:
A
/|
/ |
/ |C
O———|——D
\ |
\ |
\|
B
3. 以O'为圆心,OC为半径画弧交O'A'于C':
O'——C'——A'
4. 以C'为圆心,CD为半径画弧交前弧于D':
O'——C'——A'
\
\
D'
5. 作射线O'B':
D'
/
/
O'——C'——A'
\
\
B'
最终∠A'O'B'=∠AOB
作图原理
在△OCD 和△O'C'D' 中:
OC=O'C'(步骤 2 和 3 中截取的半径相等)
CD=C'D'(步骤 4 中截取的弧长相等)
OD=O'D'(步骤 2 和 3 中截取的半径相等)
根据 “边边边”(SSS)全等判定定理,△OCD≌△O'C'D',因此对应角相等,即∠COD=∠C'O'D',也就是∠AOB=∠A'O'B'。这就是用尺规作一个角等于已知角的理论依据。
例题解析
例 1:已知∠α,用尺规作一个角,使它等于∠α 的 2 倍。
解:作法如下:
作∠AOB=∠α(按上述用尺规作一个角等于已知角的步骤)。
以点 O 为顶点,OB 为一边,在∠AOB 的外部作∠BOC=∠α。
则∠AOC=∠AOB+∠BOC=∠α+∠α=2∠α,∠AOC 即为所求作的角。
例 2:用尺规作图,已知∠1 和∠2,作一个角等于∠1+∠2。
解:作法如下:
作射线 OA。
以 O 为顶点,OA 为一边,作∠AOB=∠1。
以 O 为顶点,OB 为一边,在∠AOB 的外部作∠BOC=∠2。
则∠AOC=∠AOB+∠BOC=∠1+∠2,∠AOC 即为所求作的角。
小练习
填空题:
(1)尺规作图的工具是______和______。
(2)用尺规作一个角等于已知角时,第 2 步和第 3 步都要画弧,其中第 2 步是以______为圆心,第 3 步是以______为圆心,且这两步画弧的半径______。
(3)用尺规作角的理论依据是全等三角形的______判定定理(SSS)。
作图题:
(1)已知∠ABC,用尺规作一个角等于∠ABC。
(2)已知∠α 和∠β(∠α>∠β),用尺规作一个角等于∠α-∠β。
简答题:
(1)在 “用尺规作一个角等于已知角” 的步骤中,为什么要保证 OC=O'C',CD=C'D',OD=O'D'?
(2)用尺规作角与用量角器画角有什么不同?
思考讨论
除了作一个角等于已知角,你认为用尺规还能作出哪些特殊角?(如 60°、30° 等)
可以作出 60° 角:因为等边三角形的三个角都是 60°,所以可以用尺规作一个等边三角形,其中的一个角就是 60°。具体步骤:作一条线段 AB,以 A 为圆心,AB 为半径画弧,以 B 为圆心,AB 为半径画弧,两弧交于点 C,连接 AC 和 BC,则∠CAB=60°。
在此基础上,可以作出 30° 角(作 60° 角的角平分线)、90° 角(作两个 60° 角的和减去 30° 角,或利用等腰直角三角形)等。
尺规作图在几何学习中的意义是什么?
尺规作图是几何的基本技能之一,它不依赖于度量,能培养学生的动手操作能力和空间想象能力;每一步操作都有严格的几何依据,有助于学生理解几何概念和定理,培养逻辑推理能力;同时,尺规作图体现了几何的严谨性和逻辑性,是后续学习复杂几何作图和证明的基础。
课堂小结
尺规作图的定义:只用圆规和无刻度直尺进行的作图,强调不依赖度量,注重操作的规范性和依据的逻辑性。
用尺规作一个角等于已知角的步骤:
作射线(起始边);
已知角上画弧(定半径,得两点);
新作射线上画弧(同半径,得对应点);
截取等长弧(定另一点);
作射线(终边)。
作图原理:通过构造全等三角形(SSS),保证所作角与已知角相等。
通过本节课的学习,我们掌握了用尺规作一个角等于已知角的方法,理解了作图的原理和每一步操作的依据。这种作图方法是几何学习中的重要工具,在后续学习角的和差、角平分线的作图等内容时会经常用到,希望同学们勤加练习,熟练掌握。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
图形的绘制,图案的设计,时常需要画线段和角.
新课导入
之前我们已经学会了用尺规作线段,那我们这节课来学一下如何用尺规作角吧!
新知探究
知识点
作一个角等于已知角
例 3 已知∠M,画∠AOB,使得∠AOB=∠M.
M
解 用量角器量得∠M=110°.
画∠AOB=110°,∠AOB即为符合题意的角.
M
O
A
B
操 作
如图,张开圆规,当圆规两足末端的距离为a时,圆规的张角为∠α. 将圆规闭合后重新张开,如何调整圆规使张角仍为∠α?
调整圆规,使圆规两足末端的距离为a ,这时圆规张角仍为∠α.
基于上面的发现,
尺规作图 作一个角等于已知角.
已知:∠AOB.
求作:∠DEF,使得∠DEF=∠AOB.
A
O
B
作法:(1)作射线EG.
(2)在∠AOB上以点O 为圆心,任意长为半径画弧,分别交射线OA和OB于点P,Q;
(3)以点E为圆心,线段OP长为半径画弧,交射线EG于点D.
A
O
B
E
G
P
Q
D
A
O
B
E
G
P
Q
D
(4)以点D 为圆心,线段PQ长为半径画弧,与(3)中所画弧交于点F;
(5)作射线EF. ∠DEF即为所求作的角.
F
例 4 如图,已知两个角∠1和∠2(∠1>∠2),求作这两个角的和.
1
2
作法 作∠AOB =∠1,以O为顶点,OB为一边在∠AOB外作∠BOC =∠2,那么∠AOC=∠1 +∠2.
1
2
O
A
B
C
1
2
1.如图,已知∠α,用尺规作∠AOB=2∠α.
练习
α
【教材P162 练习 第1题】
解:如图所示.
作法:(1)作射线OD.
(2)以∠α的顶点M为圆心,任意长为半径画弧,分别与∠α的两边交于点P,Q.
(3)以点О为圆心,线段MP长为半径画弧,交射线OD于点A.
(4)以点A为圆心,线段PQ长为半径画弧,与(3)中所画弧交于点E.
(5)以点E为圆心,线段PQ长为半径画弧,交(3)中所画弧于点B(不在OD上).
(6)作射线OB.∠AOB=2∠α即为所求作的角.
2.参考例4,作给定两角的差.
α
β
【教材P162 练习 第2题】
解:如图所示.已知∠α,∠β,求作∠α-∠β.
作法:①作∠AOC= ∠α.
②以点О为角的顶点,OC为一边,在∠AOC的内部作∠COB=∠β,则∠AOB= ∠α-∠β即为所求作的角.
1. 如图,利用尺规作图作∠AOC=∠AOB的第一步是以点О为圆心、适当长为半径作弧①,分别交OA、OB于点E、F,那么作图痕迹②的作法是( )
A. 以点F为圆心、OE长为半径作弧
B. 以点F为圆心、EF长为半径作弧
C. 以点E为圆心、OE长为半径作弧
D. 以点E为圆心、EF长为半径作弧
随堂练习
D
2. 如图①,以点B为顶点,射线BC为一边,利用尺规作图在∠CAD内部作∠EBC,使∠EBC=∠A.
解:如图②,以点B为顶点,BC为一边在∠CAD内部作∠EBC=∠A. ∠EBC即为所求作的角.
3. 如图①,已知∠α,∠β,求作一个角使它等于2∠α-∠β(保留作图痕迹,不写作法).
解: 如图,∠AOC即为所求作的2∠α-∠β.
1星题 基础练
知识点 利用尺规作一个角等于已知角
1.如图,作一个角等于已知角
(尺规作图)的正确顺序是
____________.(填序号)
2.如图,用尺规作图作的第一步是以点 为圆
心,任意长为半径画弧①,分别交,于点, ,那么
第二步的作图痕迹②的作法是( )
D
A.以点为圆心, 长为半径画弧
B.以点为圆心, 长为半径画弧
C.以点为圆心, 长为半径画弧
D.以点为圆心, 长为半径画弧
3.(8分)如图,已知 , ,作一个角,使它等于 与
的和.(不写作法,保留作图痕迹)
解:如图, 即为所求作.
2星题 中档练
4.如图, , ,根据图中尺规作
图的痕迹,可知____ .
35
5.(8分)[2025·上海月考]如图,已知 和 ,利用尺规
作,使 .
解:如图, 即为所求作的角.
3星题 提升练
6.(8分)真实情境 小亮的一张地图上有,, 三个城市,
地图上的城市被墨迹污染了(如图),但知道 ,
,请你用尺规作图的方法帮他在图中确定 城市
的具体位置.(保留作图痕迹,不写作法)
解:如图,点 即为所求.
课堂小结
步骤 作图
(1)作射线EG
(2)在∠AOB上以点O为圆心,任意长为半径画弧,分别交射线OA和OB于点P,Q
(3)以点E为圆心,线段OP长为半径画弧,交射线EG于点D
(4)以点D为圆心,线段PQ长为半径画弧,与(3)中所画弧交于点F
(5)作射线EF.∠DEF即为所求作的角
用尺规作∠DEF=∠AOB的步骤:
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
